تدوين Big O وتحليل الخوارزمية مع أمثلة Python

المُقدّمة

عادة ما توجد طرق متعددة لحل المشكلة باستخدام برنامج كمبيوتر. على سبيل المثال ، هناك عدة طرق لفرز العناصر في مصفوفة - يمكنك استخدامها دمج الفرز, فقاعة الفرز, ترتيب بالإدراج، وهلم جرا. كل هذه الخوارزميات لها مزاياها وعيوبها ، وتتمثل مهمة المطور في موازنتها حتى يتمكن من اختيار أفضل خوارزمية لاستخدامها في أي حالة استخدام. بمعنى آخر ، فإن السؤال الرئيسي هو ما هي الخوارزمية التي يجب استخدامها لحل مشكلة معينة عند وجود حلول متعددة لهذه المشكلة.

تحليل الخوارزمية يشير إلى تحليل تعقيد الخوارزميات المختلفة وإيجاد الخوارزمية الأكثر كفاءة لحل المشكلة المطروحة. تدوين Big-O هو مقياس إحصائي يستخدم لوصف مدى تعقيد الخوارزمية.

في هذا الدليل ، سنأخذ أولاً مراجعة موجزة لتحليل الخوارزمية ثم نلقي نظرة أعمق على تدوين Big-O. سنرى كيف يمكن استخدام تدوين Big-O لإيجاد تعقيد الخوارزمية بمساعدة وظائف Python المختلفة.

لماذا تحليل الخوارزمية مهم؟

لفهم سبب أهمية تحليل الخوارزمية ، سنستعين بمثال بسيط. لنفترض أن مديرًا كلف اثنين من موظفيه بتصميم خوارزمية في Python تحسب معامل الرقم الذي أدخله المستخدم. تبدو الخوارزمية التي طورها الموظف الأول كما يلي:

def fact(n):
    product = 1
    for i in range(n):
        product = product * (i+1)
    return product

print(fact(5))

لاحظ أن الخوارزمية تأخذ عددًا صحيحًا كوسيطة. داخل fact() وظيفة متغير اسمه product مهيأ إلى 1. يتم تنفيذ حلقة من 1 إلى n وأثناء كل تكرار ، تظهر القيمة في ملف product يتم ضربه في الرقم الذي يتم تكراره بواسطة الحلقة ويتم تخزين النتيجة في ملف product متغير مرة أخرى. بعد تنفيذ الحلقة ، فإن ملف product سيحتوي المتغير على العامل.

وبالمثل ، طور الموظف الثاني أيضًا خوارزمية تحسب معامل الرقم. استخدم الموظف الثاني دالة تكرارية لحساب مضروب الرقم n:

def fact2(n):
    if n == 0:
        return 1
    else:
        return n * fact2(n-1)

print(fact2(5))

يجب على المدير أن يقرر الخوارزمية التي يجب استخدامها. للقيام بذلك ، قرروا اختيار الخوارزمية التي تعمل بشكل أسرع. تتمثل إحدى طرق القيام بذلك في العثور على الوقت المطلوب لتنفيذ الكود على نفس الإدخال.

في دفتر Jupyter ، يمكنك استخدام ملف %timeit حرفية متبوعة باستدعاء الوظيفة لإيجاد الوقت الذي تستغرقه الوظيفة للتنفيذ:

%timeit fact(50)

هذا سوف يعطينا:

9 µs ± 405 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

يقول الإخراج أن الخوارزمية تأخذ ميكروثانية 9 (زائد / ناقص 45 نانوثانية) لكل حلقة.

وبالمثل ، يمكننا حساب مقدار الوقت الذي يستغرقه تنفيذ النهج الثاني:

%timeit fact2(50)

سيؤدي هذا إلى:

15.7 µs ± 427 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

تأخذ الخوارزمية الثانية التي تنطوي على العودية ميكروثانية 15 (زائد / ناقص 427 نانوثانية).

يوضح وقت التنفيذ أن الخوارزمية الأولى أسرع مقارنة بالخوارزمية الثانية التي تتضمن العودية. عند التعامل مع المدخلات الكبيرة ، يمكن أن يصبح فرق الأداء أكثر أهمية.

ومع ذلك ، فإن وقت التنفيذ ليس مقياسًا جيدًا لقياس مدى تعقيد الخوارزمية نظرًا لأنه يعتمد على الأجهزة. هناك حاجة إلى مقياس تحليل تعقيد أكثر موضوعية للخوارزمية. هذا هو المكان يا كبير التدوين يأتي للعب.

تحليل الخوارزمية باستخدام تدوين Big-O

يشير تدوين Big-O إلى العلاقة بين الإدخال إلى الخوارزمية والخطوات المطلوبة لتنفيذ الخوارزمية. يُشار إليه بحرف "O" كبير متبوعًا بقوس فتح وإغلاق. داخل الأقواس ، يتم عرض العلاقة بين المدخلات والخطوات التي اتخذتها الخوارزمية باستخدام "n".

الوجبات الجاهزة الرئيسية هي - Big-O غير مهتم بـ خاص المثال الذي تقوم فيه بتشغيل خوارزمية ، مثل fact(50)، بل إلى أي مدى يتم ذلك بشكل جيد مقياس نظرا لزيادة المدخلات. هذا مقياس أفضل بكثير للتقييم من الوقت الملموس لمثال ملموس!

على سبيل المثال ، إذا كان هناك ملف علاقة خطية بين الإدخال والخطوة التي اتخذتها الخوارزمية لإكمال تنفيذها ، سيكون تدوين Big-O المستخدم O (ن). وبالمثل ، فإن تدوين Big-O لـ وظائف من الدرجة الثانية is س (ن²).

لبناء الحدس:

• O (ن): في n=1يتم اتخاذ خطوة واحدة. في n=10، تم اتخاذ 10 خطوات.
• س (ن²): في n=1يتم اتخاذ خطوة واحدة. في n=10، تم اتخاذ 100 خطوات.

At n=1، سوف يؤدي هذان الشخصان نفس الشيء! هذا سبب آخر يجعل ملاحظة العلاقة بين المدخلات وعدد الخطوات لمعالجة هذا الإدخال أفضل من مجرد تقييم الوظائف مع بعض المدخلات الملموسة.

فيما يلي بعض وظائف Big-O الأكثر شيوعًا:

الاسم	يا كبير
ثابت	O (ج)
خطي	O (ن)
تربيعي	س (ن²)
مكعب	يا (لا)
أسي	يا (2ⁿ)
وغاريتمي	O (تسجيل (ن))
سجل خطي	O (nlog (n))

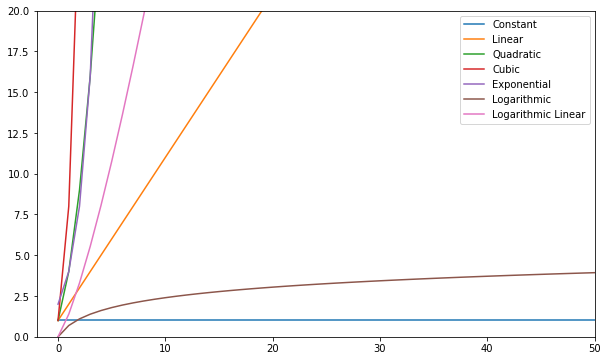
يمكنك تصور هذه الوظائف ومقارنتها:

بشكل عام - أي شيء أسوأ من الخطي يعتبر تعقيدًا سيئًا (أي غير فعال) ويجب تجنبه إن أمكن. التعقيد الخطي لا بأس به وعادة ما يكون شر لا بد منه. اللوغاريتمية جيدة. ثابت أمر مذهل!

للحصول على فكرة عن كيفية حساب Big-O ، دعنا نلقي نظرة على بعض الأمثلة على التعقيد الثابت والخطي والتربيعي.

التعقيد المستمر - يا (ج)

يقال إن تعقيد الخوارزمية ثابت إذا ظلت الخطوات المطلوبة لإكمال تنفيذ الخوارزمية ثابتة ، بغض النظر عن عدد المدخلات. يتم الإشارة إلى التعقيد المستمر بواسطة O (ج) أين c يمكن أن يكون أي رقم ثابت.

لنكتب خوارزمية بسيطة في Python تجد مربع العنصر الأول في القائمة ثم نطبعه على الشاشة:

def constant_algo(items):
    result = items[0] * items[0]
    print(result)

constant_algo([4, 5, 6, 8])

في النص أعلاه ، بغض النظر عن حجم الإدخال، أو عدد العناصر في قائمة الإدخال items، الخوارزمية تنفذ خطوتين فقط:

1. إيجاد مربع العنصر الأول
2. طباعة النتيجة على الشاشة.

ومن ثم ، فإن التعقيد يظل ثابتًا.

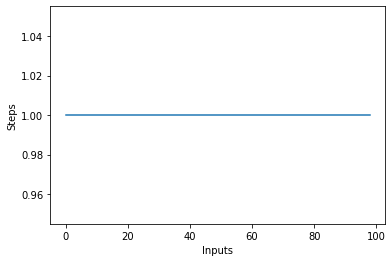
إذا قمت برسم مخطط خط بحجم متغير من items الإدخال على المحور السيني وعدد الخطوات على المحور ص ، ستحصل على خط مستقيم. لنقم بإنشاء نص قصير لمساعدتنا على تصور هذا. بغض النظر عن عدد المدخلات ، يظل عدد الخطوات المنفذة كما هو:

steps = []
def constant(n):
    return 1
    
for i in range(1, 100):
    steps.append(constant(i))
plt.plot(steps)

التعقيد الخطي - O (ن)

يقال أن تعقيد الخوارزمية يكون خطيًا إذا كانت الخطوات المطلوبة لإكمال تنفيذ الخوارزمية تزيد أو تنقص خطيًا مع عدد المدخلات. يتم الإشارة إلى التعقيد الخطي بواسطة O (ن).

في هذا المثال ، دعنا نكتب برنامجًا بسيطًا يعرض جميع العناصر الموجودة في القائمة إلى وحدة التحكم:

def linear_algo(items):
    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

تعقيد ال linear_algo() الدالة خطية في المثال أعلاه لأن عدد مرات تكرار حلقة for-loop سيكون يساوي حجم المدخلات items مجموعة. على سبيل المثال ، إذا كان هناك 4 عناصر في ملف items القائمة ، سيتم تنفيذ حلقة for-loop 4 مرات.

لنقم بسرعة بإنشاء مخطط لخوارزمية التعقيد الخطي مع عدد المدخلات على المحور السيني وعدد الخطوات على المحور الصادي:

steps = []
def linear(n):
    return n
    
for i in range(1, 100):
    steps.append(linear(i))
    
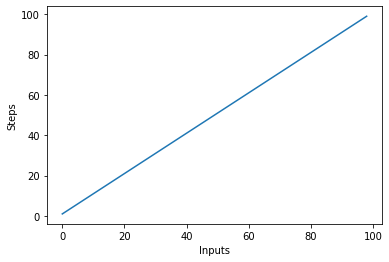
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

سيؤدي هذا إلى:

من المهم ملاحظة أنه مع المدخلات الكبيرة ، تميل الثوابت إلى فقدان قيمتها. هذا هو السبب في أننا نزيل عادةً الثوابت من تدوين Big-O ، وعادةً ما يتم اختصار تعبير مثل O (2n) إلى O (n). كل من O (2n) و O (n) خطي - العلاقة الخطية هي ما يهم ، وليس القيمة الملموسة. على سبيل المثال ، دعنا نعدل ملف linear_algo():

def linear_algo(items):
    for item in items:
        print(item)

    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

هناك نوعان من حلقات for التي تتكرر على المدخلات items قائمة. لذلك يصبح تعقيد الخوارزمية يا (2 ن)، ولكن في حالة العناصر اللانهائية في قائمة الإدخال ، فإن ضعف اللانهاية لا يزال يساوي اللانهاية. يمكننا تجاهل الثابت 2 (نظرًا لأنه غير مهم في النهاية) ولا يزال تعقيد الخوارزمية قائمًا O (ن).

دعنا نتخيل هذه الخوارزمية الجديدة من خلال رسم المدخلات على المحور السيني وعدد الخطوات على المحور ص:

steps = []
def linear(n):
    return 2*n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

في النص أعلاه ، يمكنك رؤية ذلك بوضوح ص = 2 ن، ومع ذلك ، يكون الإخراج خطيًا ويبدو كالتالي:

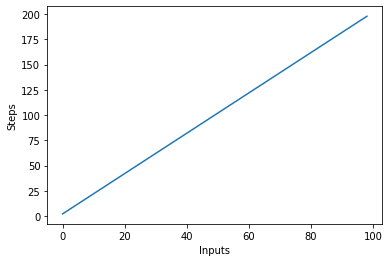
التعقيد التربيعي - س (ن²)

يُقال أن تعقيد الخوارزمية تربيعي عندما تكون الخطوات المطلوبة لتنفيذ خوارزمية دالة تربيعية لعدد العناصر في الإدخال. يتم الإشارة إلى التعقيد التربيعي على أنه س (ن²):

def quadratic_algo(items):
    for item in items:
        for item2 in items:
            print(item, ' ' ,item2)

quadratic_algo([4, 5, 6, 8])

لدينا حلقة خارجية تتكرر عبر جميع العناصر في قائمة الإدخال ثم حلقة داخلية متداخلة ، والتي تتكرر مرة أخرى عبر جميع العناصر في قائمة الإدخال. العدد الإجمالي للخطوات المنفذة هو n * n ، حيث n هو عدد العناصر في صفيف الإدخال.

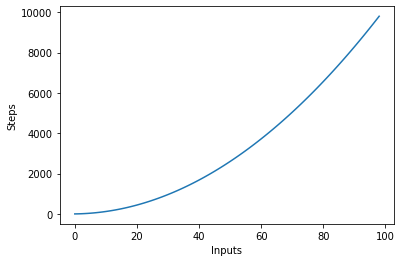
يرسم الرسم البياني التالي عدد المدخلات مقابل خطوات خوارزمية ذات تعقيد تربيعي:

التعقيد اللوغاريتمي - O (تسجيل الدخول)

تحقق بعض الخوارزميات تعقيدًا لوغاريتميًا ، مثل بحث ثنائي. يبحث البحث الثنائي عن عنصر في المصفوفة ، عن طريق التحقق من وسط من المصفوفة ، وتقليم النصف الذي لا يوجد فيه العنصر. يقوم بذلك مرة أخرى للنصف المتبقي ، ويستمر في نفس الخطوات حتى يتم العثور على العنصر. في كل خطوة ، يتم ذلك أنصاف عدد العناصر في المصفوفة.

يتطلب هذا فرز المصفوفة ، ولكي نقوم بافتراض حول البيانات (مثل أنها مرتبة).

عندما يمكنك وضع افتراضات حول البيانات الواردة ، يمكنك اتخاذ خطوات تقلل من تعقيد الخوارزمية. التعقيد اللوغاريتمي أمر مرغوب فيه ، لأنه يحقق أداءً جيدًا حتى مع وجود مدخلات عالية التحجيم.

العثور على تعقيد الوظائف المعقدة؟

في الأمثلة السابقة ، كان لدينا وظائف بسيطة إلى حد ما على المدخلات. رغم ذلك ، كيف نحسب Big-O للوظائف التي تستدعي (متعددة) وظائف أخرى على الإدخال؟

لنلقي نظرة:

def complex_algo(items):

    for i in range(5):
        print("Python is awesome")

    for item in items:
        print(item)

    for item in items:
        print(item)

    print("Big O")
    print("Big O")
    print("Big O")

complex_algo([4, 5, 6, 8])

في البرنامج النصي أعلاه ، يتم تنفيذ العديد من المهام ، أولاً ، تتم طباعة سلسلة 5 مرات على وحدة التحكم باستخدام print بيان. بعد ذلك ، نطبع قائمة الإدخال مرتين على الشاشة ، وأخيرًا ، تتم طباعة سلسلة أخرى ثلاث مرات على وحدة التحكم. للعثور على مدى تعقيد مثل هذه الخوارزمية ، نحتاج إلى تقسيم كود الخوارزمية إلى أجزاء ومحاولة إيجاد مدى تعقيد القطع الفردية. ضع علامة على مدى تعقيد كل قطعة.

في القسم الأول لدينا:

for i in range(5):
	print("Python is awesome")

تعقيد هذا الجزء يا (5) حيث يتم تنفيذ خمس خطوات ثابتة في هذا الجزء من الكود بغض النظر عن المدخلات.

بعد ذلك ، لدينا:

for item in items:
	print(item)

نحن نعلم مدى تعقيد جزء الكود أعلاه O (ن). وبالمثل ، فإن تعقيد الجزء التالي من الكود هو أيضًا O (ن):

for item in items:
	print(item)

أخيرًا ، في الجزء التالي من الكود ، تتم طباعة سلسلة ثلاث مرات ، ومن هنا يكون التعقيد يا (3):

print("Big O")
print("Big O")
print("Big O")

للعثور على التعقيد الكلي ، علينا ببساطة إضافة هذه التعقيدات الفردية:

O(5) + O(n) + O(n) + O(3)

بتبسيط ما ورد أعلاه نحصل على:

O(8) + O(2n) = O(8+2n)

قلنا سابقًا أنه عندما يصبح المدخل (الذي له طول n في هذه الحالة) كبيرًا للغاية ، تصبح الثوابت غير ذات أهمية ، أي أن ضعف أو نصف اللانهاية يظل لانهائيًا. لذلك يمكننا تجاهل الثوابت. سيكون التعقيد النهائي للخوارزمية O (ن)!

الأسوأ مقابل أفضل حالة التعقيد

عادة ، عندما يسألك شخص ما عن مدى تعقيد الخوارزمية - يكون مهتمًا بأسوأ حالة تعقيد (Big-O). في بعض الأحيان ، قد يكونون مهتمين أيضًا بأفضل حالة تعقيد (Big-Omega).

لفهم العلاقة بين هذه ، دعنا نلقي نظرة على جزء آخر من التعليمات البرمجية:

def search_algo(num, items):
    for item in items:
        if item == num:
            return True
        else:
            pass
nums = [2, 4, 6, 8, 10]

print(search_algo(2, nums))

في النص أعلاه ، لدينا وظيفة تأخذ رقمًا وقائمة من الأرقام كمدخلات. يعود صحيحًا إذا تم العثور على الرقم الذي تم تمريره في قائمة الأرقام ، وإلا فإنه يعود None. إذا كنت تبحث عن 2 في القائمة ، فسيتم العثور عليها في المقارنة الأولى. هذه هي أفضل حالة تعقيد للخوارزمية حيث تم العثور على العنصر الذي تم البحث عنه في الفهرس الأول الذي تم البحث فيه. أفضل حالة تعقيد، في هذه الحالة ، هو يا (1). من ناحية أخرى ، إذا قمت بالبحث عن 10 ، فسيتم العثور عليه في آخر فهرس تم البحث عنه. سيتعين على الخوارزمية البحث في جميع العناصر الموجودة في القائمة ، وبالتالي التعقيد الأسوأ يصبح O (ن).

بالإضافة إلى حالة التعقيد الأفضل والأسوأ ، يمكنك أيضًا الحساب متوسط ​​التعقيد (Big-Theta) من خوارزمية ، والتي تخبرك "بالنظر إلى إدخال عشوائي ، ما هو الوقت المتوقع من التعقيد للخوارزمية"؟

تعقيد الفضاء

بالإضافة إلى تعقيد الوقت ، حيث تحسب عدد الخطوات المطلوبة لإكمال تنفيذ الخوارزمية ، يمكنك أيضًا العثور على تعقيد الفضاء والتي تشير إلى مقدار المساحة التي تحتاج إلى تخصيصها في الذاكرة أثناء تنفيذ البرنامج.

ألق نظرة على المثال التالي:

def return_squares(n):
    square_list = []
    for num in n:
        square_list.append(num * num)

    return square_list

nums = [2, 4, 6, 8, 10]
print(return_squares(nums))

• return_squares() دالة تقبل قائمة الأعداد الصحيحة وترجع قائمة بالمربعات المقابلة. يجب أن تخصص الخوارزمية ذاكرة لنفس عدد العناصر كما في قائمة الإدخال. لذلك ، يصبح تعقيد مساحة الخوارزمية O (ن).

وفي الختام

تدوين Big-O هو المقياس القياسي المستخدم لقياس مدى تعقيد الخوارزمية. في هذا الدليل ، درسنا ماهية تدوين Big-O وكيف يمكن استخدامه لقياس مدى تعقيد مجموعة متنوعة من الخوارزميات. لقد درسنا أيضًا أنواعًا مختلفة من وظائف Big-O بمساعدة أمثلة Python المختلفة. أخيرًا ، استعرضنا بإيجاز حالة التعقيد الأسوأ والأفضل جنبًا إلى جنب مع تعقيد الفضاء.