تم العثور على "تذمرات" المنحنى الإهليلجي باستخدام الذكاء الاصطناعي لرحلة الطيران | مجلة كوانتا

المنحنيات الإهليلجية هي من بين الأشياء الأكثر خداعًا في الرياضيات الحديثة. لا تبدو معقدة، لكنها تشكل طريقًا سريعًا بين الرياضيات التي يتعلمها الكثير من الناس في المدرسة الثانوية والبحث في الرياضيات في أكثر حالاتها غموضًا. لقد كانت محورية في إثبات أندرو وايلز الشهير لنظرية فيرما الأخيرة في التسعينيات. إنها أدوات أساسية في التشفير الحديث. وفي عام 1990، قام معهد كلاي للرياضيات بتسمية أ تخمين حول الإحصائيات واحدة من سبع "مسائل جائزة الألفية" التي تحمل كل واحدة منها جائزة قدرها مليون دولار لحلها. هذا التخمين، غامر لأول مرة من قبل بريان بيرش و بيتر سوينرتون داير في الستينيات، ولم يتم إثباته بعد.

إن فهم المنحنيات الإهليلجية هو مسعى عالي المخاطر وكان محوريًا في الرياضيات. لذلك، في عام 2022، عندما استخدم التعاون عبر الأطلسي التقنيات الإحصائية والذكاء الاصطناعي لاكتشاف أنماط غير متوقعة تمامًا في المنحنيات الإهليلجية، كانت هذه مساهمة مرحب بها، وإن كانت غير متوقعة. قال: "لقد كانت مسألة وقت فقط قبل أن يصل التعلم الآلي إلى عتبة بابنا بشيء مثير للاهتمام". بيتر سارناك، عالم رياضيات في معهد الدراسات المتقدمة وجامعة برينستون. في البداية، لم يتمكن أحد من تفسير سبب وجود الأنماط المكتشفة حديثًا. منذ ذلك الحين، وفي سلسلة من الأوراق البحثية الحديثة، بدأ علماء الرياضيات في كشف الأسباب الكامنة وراء هذه الأنماط، التي يطلق عليها اسم "التذمرات" لتشابهها مع الأشكال السائلة لأسراب الزرزور، وبدأوا في إثبات أنها يجب أن تحدث ليس فقط في مكان محدد. الأمثلة التي تم فحصها في عام 2022، ولكن في المنحنيات الإهليلجية بشكل عام.

أهمية أن تكون إهليلجيا

لفهم ماهية هذه الأنماط، علينا أن نضع القليل من الأساس حول ماهية المنحنيات الإهليلجية وكيف يصنفها علماء الرياضيات.

يربط المنحنى الإهليلجي بمربع متغير واحد، ويُكتب عادةً كـ y، إلى القوة الثالثة للآخر، وعادة ما يتم كتابتها كـ x: y² = x³ + Ax + B، لبعض أزواج الأرقام A و B، طالما A و B تلبية بعض الشروط المباشرة. تحدد هذه المعادلة منحنى يمكن رسمه بيانيا على المستوى، كما هو موضح أدناه. (على الرغم من التشابه في الأسماء، فإن القطع الناقص ليس منحنى إهليلجيا).

على الرغم من أن المنحنيات الإهليلجية تبدو بسيطة، فقد تبين أنها أدوات قوية بشكل لا يصدق لمنظري الأعداد - علماء الرياضيات الذين يبحثون عن أنماط في الأعداد الصحيحة. بدلا من السماح للمتغيرات x و y على جميع الأعداد، يحب علماء الرياضيات حصرها في أنظمة أرقام مختلفة، وهو ما يسمونه تعريف المنحنى "فوق" نظام أرقام معين. تعتبر المنحنيات الإهليلجية التي تقتصر على الأعداد النسبية - الأرقام التي يمكن كتابتها على شكل كسور - مفيدة بشكل خاص. وقال سارناك: "إن المنحنيات الإهليلجية فوق الأعداد الحقيقية أو المعقدة مملة للغاية". "إنها فقط الأرقام المنطقية العميقة."

وإليك طريقة واحدة وهذا صحيح. إذا رسمت خطًا مستقيمًا بين نقطتين نسبيتين على منحنى إهليلجي، فإن المكان الذي يتقاطع فيه هذا الخط مع المنحنى مرة أخرى سيكون عقلانيًا أيضًا. يمكنك استخدام هذه الحقيقة لتعريف "الإضافة" في منحنى إهليلجي، كما هو موضح أدناه.

رسم خط بين P و Q. سيتقاطع هذا الخط مع المنحنى عند النقطة الثالثة، R. (لدى علماء الرياضيات خدعة خاصة للتعامل مع الحالة التي لا يتقاطع فيها الخط مع المنحنى عن طريق إضافة "نقطة عند اللانهاية".) R عبر x-المحور هو مجموعك P + Q. جنبًا إلى جنب مع عملية الجمع هذه، تشكل جميع حلول المنحنى كائنًا رياضيًا يسمى المجموعة.

يستخدم علماء الرياضيات هذا لتحديد "رتبة" المنحنى. ال رتبة منحنى يتعلق بعدد الحلول العقلانية التي لديه. منحنيات الرتبة 0 لها عدد محدود من الحلول. تحتوي المنحنيات ذات الرتبة الأعلى على عدد لا حصر له من الحلول التي يتم وصف علاقتها ببعضها البعض باستخدام عملية الجمع بواسطة الرتبة.

الرتب ليست مفهومة جيدا؛ لا يملك علماء الرياضيات دائمًا طريقة لحسابها، ولا يعرفون حجمها الذي يمكن أن يصلوا إليه. (أكبر رتبة دقيقة معروفة لمنحنى معين هي 20.) يمكن أن تحتوي المنحنيات المتشابهة على رتب مختلفة تمامًا.

للمنحنيات الإهليلجية أيضًا علاقة كبيرة بالأعداد الأولية، التي لا تقبل القسمة إلا على 1 وعلى نفسها. على وجه الخصوص، ينظر علماء الرياضيات إلى المنحنيات عبر المجالات المحدودة - أنظمة الحساب الدوري التي يتم تعريفها لكل رقم أولي. الحقل المحدود يشبه الساعة التي عدد ساعاتها يساوي العدد الأولي: إذا واصلت العد للأعلى، فإن الأرقام تبدأ من جديد. في المجال المحدود للرقم 7، على سبيل المثال، 5 زائد 2 يساوي صفرًا، و5 زائد 3 يساوي 1.

يحتوي المنحنى الإهليلجي على تسلسل مرتبط من الأرقام يسمى a_p، والذي يتعلق بعدد الحلول الموجودة للمنحنى في المجال المحدود المحدد بواسطة الأولي p. أصغر a_p يعني المزيد من الحلول؛ أكبر a_p يعني حلول أقل على الرغم من صعوبة حساب الرتبة، إلا أن التسلسل a_p أسهل بكثير.

على أساس العديد من الحسابات التي تم إجراؤها على أحد أجهزة الكمبيوتر الأولى، توقع بيرش وسوينرتون-داير وجود علاقة بين رتبة المنحنى الإهليلجي والتسلسل a_p. أي شخص يستطيع إثبات أنه كان على حق سيفوز بمليون دولار والخلود الرياضي.

ظهور نمط مفاجئ

بعد بداية الوباء. يانغ هوي هيقرر الباحث في معهد لندن للعلوم الرياضية مواجهة بعض التحديات الجديدة. كان متخصصًا في الفيزياء في الكلية، وحصل على الدكتوراه من معهد ماساتشوستس للتكنولوجيا في الفيزياء الرياضية. لكنه كان مهتمًا بشكل متزايد بنظرية الأعداد، ونظرًا للقدرات المتزايدة للذكاء الاصطناعي، اعتقد أنه سيحاول استخدام الذكاء الاصطناعي كأداة للعثور على أنماط غير متوقعة في الأرقام. (لقد كان كذلك بالفعل باستخدام التعلم الآلي تصنيف متشعبات كالابي ياو، الهياكل الرياضية المستخدمة على نطاق واسع في نظرية الأوتار.)

في أغسطس 2020، مع تفاقم الوباء، استضافته جامعة نوتنغهام لحضور لقاء الحديث عبر الإنترنت. لقد كان متشائمًا بشأن التقدم الذي أحرزه، وبشأن إمكانية استخدام التعلم الآلي للكشف عن رياضيات جديدة. وقال: "كانت روايته هي أن نظرية الأعداد كانت صعبة لأنه لا يمكنك التعلم الآلي للأشياء في نظرية الأعداد". توماس أوليفر، عالم الرياضيات في جامعة وستمنستر الذي كان من بين الحضور. وكما يتذكر، "لم أتمكن من العثور على أي شيء لأنني لم أكن خبيراً. لم أكن حتى أستخدم الأشياء الصحيحة للنظر إلى هذا.

أوليفر و كيو هوان لي، عالم الرياضيات في جامعة كونيتيكت، بدأ العمل مع هي. وقال أوليفر: "لقد قررنا القيام بذلك فقط لمعرفة ماهية التعلم الآلي، بدلاً من دراسة الرياضيات بجدية". "لكننا اكتشفنا بسرعة أنه يمكنك تعلم الكثير من الأشياء آليًا."

اقترح أوليفر ولي أن يطبق تقنياته في الفحص L- وظائف سلسلة لا نهائية ترتبط ارتباطًا وثيقًا بالمنحنيات الإهليلجية من خلال التسلسل a_p. ويمكنهم استخدام قاعدة بيانات على الإنترنت للمنحنيات الإهليلجية وما يرتبط بها L- وظائف تسمى LMFDB لتدريب مصنفات التعلم الآلي الخاصة بهم. في ذلك الوقت، كانت قاعدة البيانات تحتوي على ما يزيد قليلاً عن 3 ملايين منحنى إهليلجي فوق الحدود المنطقية. بحلول أكتوبر 2020، كان لديهم ورقة التي تستخدم المعلومات المستمدة من L- وظائف للتنبؤ بخاصية معينة للمنحنيات الإهليلجية. في نوفمبر شاركوا ورقة أخرى التي استخدمت التعلم الآلي لتصنيف الكائنات الأخرى في نظرية الأعداد. وبحلول ديسمبر/كانون الأول، كانوا قادرين على ذلك التنبؤ بصفوف المنحنيات الإهليلجية بدقة عالية.

لكنهم لم يكونوا متأكدين من سبب عمل خوارزميات التعلم الآلي الخاصة بهم بشكل جيد. طلب لي من طالبه الجامعي أليكسي بوزدنياكوف معرفة ما إذا كان بإمكانه معرفة ما يجري. وفي الواقع، يقوم LMFDB بفرز المنحنيات الإهليلجية وفقًا لكمية تسمى الموصل، والتي تلخص المعلومات حول الأعداد الأولية التي يفشل المنحنى في التصرف بها بشكل جيد. لذلك حاول بوزدنياكوف النظر إلى أعداد كبيرة من المنحنيات ذات الموصلات المتشابهة في وقت واحد، على سبيل المثال، جميع المنحنيات ذات الموصلات بين 7,500 و10,000.

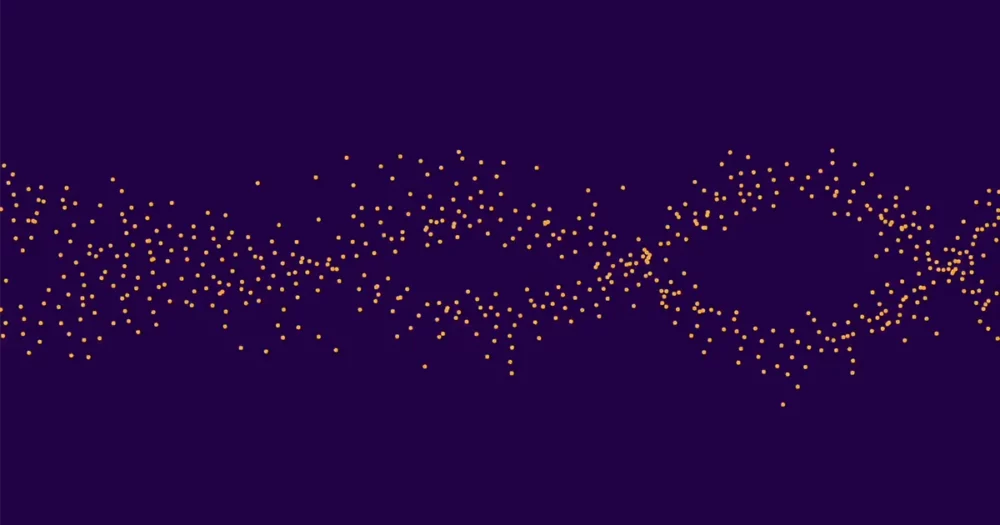
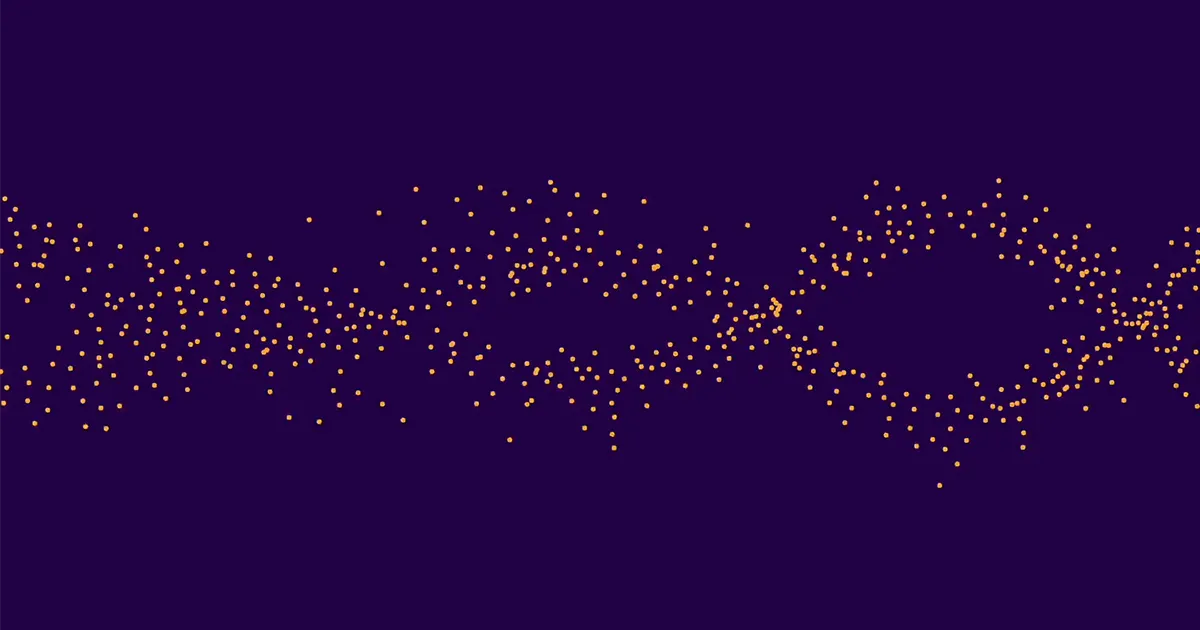
وبلغ هذا حوالي 10,000 منحنيات في المجموع. حوالي نصف هؤلاء حصلوا على الرتبة 0، والنصف الآخر حصلوا على الرتبة 1. (الرتب الأعلى نادرة جدًا). ​​ثم قام بحساب متوسط ​​قيم a_p لجميع منحنيات الرتبة 0، متوسطها بشكل منفصل a_p لجميع منحنيات الرتبة 1، ورسم النتائج. شكلت مجموعتا النقاط موجتين متميزتين يمكن تمييزهما بسهولة. ولهذا السبب تمكنت مصنفات التعلم الآلي من التأكد بشكل صحيح من صفوف منحنيات معينة.

قال بوزدنياكوف: "في البداية شعرت بالسعادة لأنني أكملت المهمة". "لكن كيو-هوان أدرك على الفور أن هذا النمط كان مفاجئًا، وعندها أصبح الأمر مثيرًا حقًا."

كان لي وأوليفر مفتونين. قال أوليفر: "أظهر لنا أليكسي الصورة، وقلت إنها تبدو مثل ذلك الشيء الذي تفعله الطيور". "ثم بحث كيو-هوان عنه وقال إنه يسمى همهمة، ثم قال يانغ أننا يجب أن نطلق على الصحيفة"تذمر المنحنيات الإهليلجية".

لقد قاموا بتحميل ورقتهم البحثية في أبريل 2022 وأرسلوها إلى مجموعة من علماء الرياضيات الآخرين، متوقعين بعصبية أن يتم إخبارهم بأن ما يسمى بـ "اكتشافهم" معروف جيدًا. قال أوليفر إن العلاقة كانت واضحة جدًا لدرجة أنه كان ينبغي ملاحظتها منذ فترة طويلة.

على الفور تقريبًا، حظيت النسخة الأولية بالاهتمام، خاصة من أندرو ساذرلاند، عالم أبحاث في معهد ماساتشوستس للتكنولوجيا وأحد مديري تحرير LMFDB. أدرك ساذرلاند أن 3 ملايين منحنيات إهليلجية لم تكن كافية لتحقيق أهدافه. لقد أراد أن ينظر إلى نطاقات موصلات أكبر بكثير ليرى مدى قوة التذمر. لقد قام بسحب البيانات من مستودع هائل آخر يضم حوالي 150 مليون منحنى إهليلجي. وبعد أن ظل غير راضٍ، قام بعد ذلك بسحب البيانات من مستودع مختلف يحتوي على 300 مليون منحنى.

قال ساذرلاند: "لكن حتى تلك لم تكن كافية، لذلك قمت بالفعل بحساب مجموعة بيانات جديدة تضم أكثر من مليار منحنى إهليلجي، وهذا ما استخدمته لحساب الصور عالية الدقة حقًا". أظهرت التذمرات ما إذا كان متوسطه أكثر من 15,000 منحنيات إهليلجية في المرة الواحدة أو مليون في المرة الواحدة. بقي الشكل كما هو حتى عندما نظر إلى المنحنيات فوق الأعداد الأولية الأكبر والأكبر، وهي ظاهرة تسمى ثبات المقياس. أدرك ساذرلاند أيضًا أن التذمر لا يقتصر على المنحنيات الإهليلجية، ولكنه يظهر أيضًا بشكل أكثر عمومية L-المهام. هو كتب رسالة تلخص النتائج التي توصل إليها وأرسلها إلى سارناك و مايكل روبنشتاين في جامعة واترلو.

وكتب ساذرلاند: "إذا كان هناك تفسير معروف لذلك، فأنا أتوقع أنك ستعرفه".

لم يفعلوا.

شرح النمط

نظم لي وهي وأوليفر ورشة عمل حول التذمر في أغسطس 2023 في معهد البحوث الحسابية والتجريبية في الرياضيات (ICERM) بجامعة براون. جاء سارناك وروبنشتاين، كما فعل تلميذ سارناك نينا زوبريلينا.

قدمت زوبريلينا بحثها عن أنماط التذمر في أشكال وحدات، وظائف معقدة خاصة ترتبط، مثل المنحنيات الإهليلجية L-المهام. في الأشكال المعيارية ذات الموصلات الكبيرة، تتقارب النفخات في منحنى محدد بشكل حاد، بدلاً من تشكيل نمط واضح ولكنه مشتت. في ورقة وقد أثبتت زوبريلينا، التي نُشرت في 11 أكتوبر 2023، أن هذا النوع من التذمر يتبع صيغة صريحة اكتشفتها.

"إن الإنجاز الكبير الذي حققته نينا هو أنها أعطت صيغة لهذا؛ قال سارناك: "أنا أسميها صيغة كثافة نفخة زوبريلينا". "باستخدام الرياضيات المعقدة للغاية، أثبتت معادلة دقيقة تناسب البيانات تمامًا."

صيغتها معقدة، لكن سارناك يشيد بها باعتبارها نوعًا جديدًا مهمًا من الوظائف، يمكن مقارنتها بدوال إيري التي تحدد حلول المعادلات التفاضلية المستخدمة في مجموعة متنوعة من السياقات في الفيزياء، بدءًا من البصريات إلى ميكانيكا الكم.

على الرغم من أن صيغة زوبريلينا كانت الأولى، فقد تبعتها وصفات أخرى. قال سارناك: "في كل أسبوع، يتم إصدار بحث جديد، يستخدم بشكل أساسي أدوات زوبريلينا، ويشرح جوانب أخرى من التذمر".

جوناثان بوبر, أندرو بوكر و مين لي من جامعة بريستول، بالتعاون مع ديفيد لوري دودا من ICERM، أثبت وجود نوع مختلف من النفخة في أشكال وحدات في ورقة أكتوبر أخرى. وكيو هوان لي وأوليفر وبوزدنياكوف أثبت الوجود من التذمر في الأشياء التي تسمى أحرف Dirichlet والتي ترتبط ارتباطًا وثيقًا بها L-المهام.

أعجب ساذرلاند بجرعة الحظ الكبيرة التي أدت إلى اكتشاف التذمر. إذا لم يتم طلب بيانات المنحنى الإهليلجي من قبل الموصل، لكانت التذمرات قد اختفت. وقال: "لقد كانوا محظوظين بأخذ البيانات من LMFDB، والتي جاءت مرتبة مسبقًا وفقًا للموصل". "هذا هو ما يربط المنحنى الإهليلجي بالشكل المعياري المقابل، لكن هذا ليس واضحًا على الإطلاق. … منحنيان تبدو معادلاتهما متشابهة جدًا يمكن أن يكون لهما موصلات مختلفة تمامًا. على سبيل المثال، أشار ساذرلاند إلى ذلك y² = x³ - 11x + 6 لديه موصل 17، ولكن قلب علامة الطرح إلى علامة زائد، y² = x³ + 11x + 6 لديه موصل 100,736.

وحتى ذلك الحين، لم يتم العثور على التذمر إلا بسبب قلة خبرة بوزدنياكوف. وقال أوليفر: "لا أعتقد أننا كنا سنكتشف ذلك بدونه، لأن الخبراء عادة ما يقومون بالتطبيع". a_p أن تكون لها قيمة مطلقة 1. لكنه لم يقوم بتطبيعها… لذلك كانت التذبذبات كبيرة جدًا وواضحة”.

وأشار أوليفر إلى أن الأنماط الإحصائية التي تستخدمها خوارزميات الذكاء الاصطناعي لفرز المنحنيات الإهليلجية حسب الرتبة موجودة في مساحة معلمات تحتوي على مئات الأبعاد، وهي أعداد كثيرة جدًا بحيث يتعذر على الأشخاص فرزها في أذهانهم، ناهيك عن تصورها. ولكن على الرغم من أن التعلم الآلي اكتشف التذبذبات الخفية، إلا أنه "في وقت لاحق فقط فهمنا أنها همهمة".

ملاحظة المحرر: أندرو ساذرلاند، وكيو هوان لي، وقاعدة بيانات الوظائف L والأشكال المعيارية (LMFDB) حصلوا جميعًا على تمويل من مؤسسة سيمونز، التي تمول أيضًا هذا المنشور المستقل تحريريًا. ليس لقرارات تمويل مؤسسة سيمونز أي تأثير على تغطيتنا. مزيد من المعلومات متاحة هنا.