نموذج خليط عملية Dirichlet

• 23 حزيران، 2014
• فاسيليس فرينيوتيس
• . 2 تعليقات

منشور المدونة هذا هو الجزء الرابع من السلسلة في التجميع باستخدام نماذج خليط عملية ديريتشليت. ناقشنا في المقالات السابقة نماذج Finite Dirichlet Mixture وأخذنا حد نموذجها لمجموعات k اللانهائية مما أدى بنا إلى إدخال عمليات Dirichlet. كما رأينا ، هدفنا هو بناء نموذج خليط لا يتطلب منا تحديد عدد مجموعات / مكونات k من البداية. بعد تقديم تمثيلات مختلفة لعمليات ديريتشليت، لقد حان الوقت الآن لاستخدام DPs فعليًا لبناء نموذج مختلط لانهائي يمكّننا من إجراء التجميع. الهدف من هذه المقالة هو تحديد نماذج مزيج عملية Dirichlet ومناقشة استخدام عملية المطعم الصيني وأخذ عينات جيبس. إذا لم تكن قد قرأت المنشورات السابقة ، فمن المستحسن بشدة القيام بذلك لأن الموضوع نظري بعض الشيء ويتطلب فهمًا جيدًا لبناء النموذج.

تحديث: أصبح Datumbox Machine Learning Framework مفتوح المصدر ومجانيًا الآن بإمكانك تحميله. تحقق من الحزمة com.datumbox.framework.machinelearning.clustering لرؤية تنفيذ نماذج Dirichlet Process Mixture Models في Java.

1. تعريف نموذج خليط عملية ديريتشليت

يتيح لنا استخدام عمليات Dirichlet الحصول على نموذج مختلط بمكونات لا نهائية يمكن اعتبارها بمثابة أخذ حد النموذج المحدود لـ k إلى ما لا نهاية. لنفترض أن لدينا النموذج التالي:

المعادلة 1: نموذج خليط عملية ديريتشليت

حيث يتم تعريف G على أنها و تستخدم كتدوين قصير لـ وهي دالة دلتا تأخذ 1 إذا و 0 في أي مكان آخر. θ_i هي معلمات الكتلة التي تم أخذ عينات منها من G. يتم تكوين التوزيع التوليدي F بواسطة معلمات الكتلة θ_i ويستخدم لتوليد x_i الملاحظات. أخيرًا يمكننا تحديد توزيع الكثافة وهو توزيع الخليط لدينا (خليط لانهائي معدود) بنسب خلط وخلط المكونات .

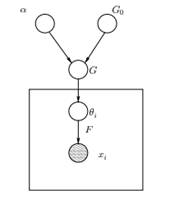
الشكل 1: نموذج رسومي لنموذج خليط عملية ديريتشليت

أعلاه يمكننا أن نرى النموذج الرسومي المكافئ لـ DPMM. إن G₀ هو التوزيع الأساسي لـ DP وعادةً ما يتم اختياره ليكون مترافقًا قبل التوزيع التوليدي الخاص بنا من أجل تسهيل العمليات الحسابية والاستفادة من الخصائص الرياضية الجذابة. α هي المعلمة الفائقة العددية لعملية Dirichlet وتؤثر على عدد المجموعات التي سنحصل عليها. كلما زادت قيمة α ، زادت المجموعات ؛ كلما كانت α أصغر كلما قل عدد المجموعات. يجب أن نلاحظ أن قيمة α تعبر عنها قوة الإيمان في G₀. تشير القيمة الكبيرة إلى أن معظم العينات ستكون مميزة ولها قيم مركزة على G₀. G هو توزيع عشوائي على مساحة المعلمة المأخوذة من DP الذي يخصص الاحتمالات للمعلمات. θ_i هو متجه معلمة مستمد من توزيع G ويحتوي على معلمات الكتلة ، ويتم تحديد معلمات توزيع F بواسطة θ_i و x_i هي نقطة البيانات التي تم إنشاؤها بواسطة التوزيع التوليدي F.

من المهم ملاحظة أن θ_i هي عناصر من مساحة المعلمة وهي "تكوين" مجموعاتنا. يمكن أيضًا اعتبارها متغيرات كامنة في x_i التي تخبرنا من أي مكون / عنقود x_i يأتي من وما هي معلمات هذا المكون. وهكذا لكل س_i التي نلاحظها ، نرسم θ_i من توزيع G. مع كل رسم يتغير التوزيع حسب التحديدات السابقة. كما رأينا في مخطط جرة Blackwell-MacQueen ، يمكن دمج توزيع G وتحديد اختياراتنا المستقبلية لـ θ_i تعتمد فقط على G₀: . لا يكون تقدير المعلمات θi من الصيغة السابقة ممكنًا دائمًا لأن العديد من التطبيقات (مثل عملية المطعم الصيني) تتضمن التعداد من خلال زيادة مكونات k أضعافا مضاعفة. وبالتالي يتم استخدام طرق حسابية تقريبية مثل أخذ عينات جيبس. أخيرًا ، يجب أن نلاحظ أنه على الرغم من أن مجموعات k لا نهائية ، فإن عدد المجموعات النشطة هو . وهكذا فإن θ_i سيكرر ويظهر تأثير التجميع.

2. استخدام عملية المطعم الصيني لتعريف نموذج الخلطة اللانهائية

النموذج المحدد في المقطع السابق صلب من الناحية الحسابية ، ومع ذلك فإن له عيبًا كبيرًا: لكل x جديد_i التي لاحظناها ، يجب علينا أخذ عينة جديدة θ_i مع مراعاة القيم السابقة لـ θ. تكمن المشكلة في أنه في كثير من الحالات ، يمكن أن يكون أخذ عينات من هذه المعلمات مهمة صعبة ومكلفة من الناحية الحسابية.

نهج بديل هو استخدام عملية المطعم الصيني لنمذجة المتغيرات الكامنة ض_i من التعيينات العنقودية. بهذه الطريقة بدلاً من استخدام θ_i للدلالة على كل من معلمات الكتلة وتخصيصات المجموعة ، نستخدم المتغير الكامن z_i للإشارة إلى معرف الكتلة ثم استخدام هذه القيمة لتعيين معلمات الكتلة. نتيجة لذلك ، لم نعد بحاجة إلى أخذ عينة من a θ في كل مرة نحصل فيها على ملاحظة جديدة ، ولكن بدلاً من ذلك نحصل على تعيين المجموعة عن طريق أخذ العينات z_i من CRP. باستخدام هذا المخطط ، يتم أخذ عينات θ جديدة فقط عندما نحتاج إلى إنشاء كتلة جديدة. نقدم أدناه نموذجًا لهذا النهج:

المعادلة 2: نموذج الخليط مع CRP

ما ورد أعلاه هو نموذج توليدي يصف كيف البيانات س_i ويتم إنشاء المجموعات. لإجراء تحليل الكتلة ، يجب علينا استخدام الملاحظات x_i وتقدير تخصيصات المجموعة ض_i.

3. استدلال نموذج الخليط وأخذ عينات جيبس

لسوء الحظ ، نظرًا لأن عمليات Dirichlet غير معلمية ، فإننا لا يمكن استخدام خوارزمية EM لتقدير المتغيرات الكامنة التي تخزن تخصيصات المجموعة. لتقدير التخصيصات ، سنستخدم ملف أخذ عينات جيبس ​​المنهارة.

عينة غيبس المنهارة هي خوارزمية ماركوف تشين مونت كارلو (MCMC) البسيطة. إنه سريع ويمكّننا من دمج بعض المتغيرات أثناء أخذ عينة من متغير آخر. ومع ذلك ، تتطلب هذه الخوارزميات منا اختيار G₀ وهو اقتران سابق للتوزيع التوليدي F من أجل التمكن من حل المعادلات تحليليًا والقدرة على أخذ عينات مباشرة من .

فيما يلي خطوات أخذ عينات جيبس ​​المطوية التي سنستخدمها لتقدير تعيينات المجموعة:

• تهيئة z_i التخصيصات العنقودية بشكل عشوائي
• كرر حتى التقارب
• حدد الفأس بشكل عشوائي_i
  
• الحفاظ على z الأخرى_j ثابت لكل j ≠ i:
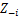
• قم بتعيين قيمة جديدة على z_i بحساب "احتمال CRP" الذي يعتمد على z_j و x_j من كل j ≠ i:

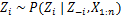
في المقالة التالية سوف نركز على كيفية إجراء تحليل الكتلة باستخدام نماذج Dirichlet Process Mixture. سنحدد نموذجين مختلفين لمزيج عمليات Dirichlet اللذان يستخدمان عملية المطعم الصيني وأخذ عينات جيبس ​​المنهارة من أجل إجراء التجميع على مجموعات البيانات والمستندات المستمرة.