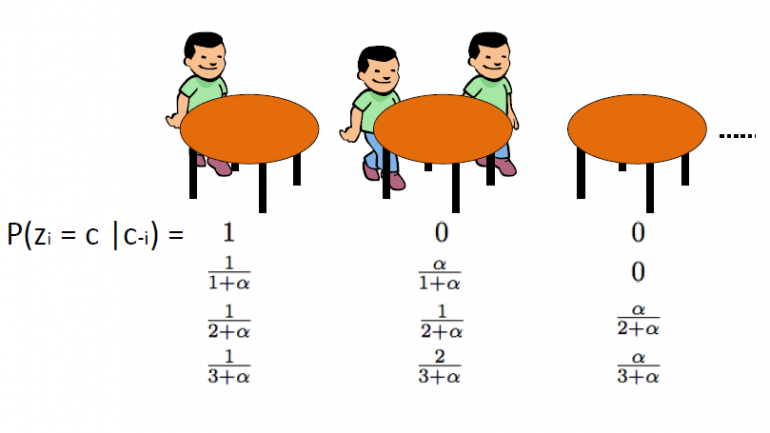عملية Dirichlet عملية المطاعم الصينية والتمثيلات الأخرى

• 20 مايو 2014
• فاسيليس فرينيوتيس
• . لا تعليق

هذه المقالة هي الجزء الثالث من السلسلة حول التكتل باستخدام نماذج Dirichlet Process Mixture. في المرة السابقة حددنا نموذج المزيج المحدود بناءً على توزيع Dirichlet وطرحنا أسئلة حول كيفية جعل هذا النموذج المعين بلا حدود. ناقشنا بإيجاز فكرة أخذ حد النموذج عندما يميل عدد k من العناقيد إلى ما لا نهاية ولكن كما أكدنا على أن وجود مثل هذا الشيء ليس تافهًا (وبعبارة أخرى ، كيف "نأخذ بالفعل حد النموذج" "؟). للتذكير ، السبب وراء رغبتنا في جعل k لانهائية هو أنه بهذه الطريقة سيكون لدينا نموذج غير معياري لا يتطلب منا تحديد العدد الإجمالي للمجموعات داخل البيانات.

تحديث: أصبح Datumbox Machine Learning Framework مفتوح المصدر ومجانيًا الآن بإمكانك تحميله. تحقق من الحزمة com.datumbox.framework.machinelearning.clustering لرؤية تنفيذ نماذج Dirichlet Process Mixture Models في Java.

على الرغم من أن هدفنا هو بناء نموذج قادر على أداء التجميع على مجموعات البيانات ، قبل ذلك يجب علينا مناقشة عمليات Dirichlet. سنقدم كل من التعريفات الرياضية الصارمة والتفسيرات الأكثر بديهية لـ DP وسنناقش طرق بناء العملية. يمكن النظر إلى هذه الإنشاءات / التوضيحات على أنها وسيلة للعثور على حدوث عملية Dirichlet في "الحياة الحقيقية".

على الرغم من أنني حاولت تكييف تقريري البحثي بطريقة تجعل متابعة مشاركات المدونة هذه أسهل ، إلا أنه لا يزال من المهم تحديد الأدوات والتوزيعات الرياضية اللازمة قبل أن ننتقل إلى استخدام النماذج. تعتبر نماذج Dirichlet Process موضوعًا للبحث النشط ، ولكنها تتطلب فهمًا جيدًا للإحصاءات والعمليات العشوائية قبل استخدامها. مشكلة أخرى هي أنه كما سنرى في هذه المقالة ، يمكن تمثيل / إنشاء عمليات Dirichlet بطرق عديدة. ونتيجة لذلك ، تستخدم العديد من الأوراق الأكاديمية تدوينًا / اصطلاحات مختلفة تمامًا وتفحص المشكلة من وجهات نظر مختلفة. في هذا المنشور ، أحاول شرحها بأبسط ما يمكن واستخدام نفس الترميز. نأمل أن تصبح الأمور أكثر وضوحًا مع المادتين القادمتين اللتين تركزان على تعريف نماذج Dirichlet Process Mixture Models وكيفية استخدامها في الواقع لإجراء تحليل الكتلة.

1. تعريف عملية Dirichlet

عملية Dirichlet على مسافة is هي عملية عشوائية. هو توزيع احتمالي على "التوزيعات الاحتمالية عبر الفضاء" و a الاستفادة منه هو توزيع منفصل. إن توزيع Dirichlet بشكل أكثر رسمية هو توزيع على مقاييس الاحتمالية. أ مقياس الاحتمالية هي دالة لمجموعات فرعية من Θ إلى [0,1،XNUMX]. G هو مقياس الاحتمال العشوائي الموزع DP ، إذا كان لأي قسم (أ₁،…أ_n) من الفضاء Θ لدينا ذلك .

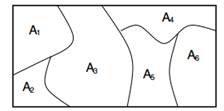
الشكل 1: يتم توزيع الهوامش الموجودة على أقسام iteite على Dirichlet.

يحتوي DP على معلمتين: الأولى هي التوزيع الأساسي G₀ الذي يخدم مثل المتوسط . والثاني هو معلمة القوة α وهي إيجابية تمامًا وتعمل مثل التباين العكسي . يحدد مدى تكرار قيم توزيع المخرجات. كلما زادت قيمة a ، كلما كان التكرار أصغر ؛ كلما كانت القيمة أصغر ، كلما زاد تكرار قيم توزيع المخرجات. وأخيرًا ، Θ space هي مساحة المعلمة التي نحدد عليها DP. علاوة على ذلك ، فإن المسافة also هي أيضًا مساحة تعريف G₀ وهو نفس الشيء مثل G.

أبسط وأكثر طريقة بديهية لشرح عملية Dirichlet هو ما يلي. افترض أن لدينا مساحة can يمكن تقسيمها بأي طريقة محدودة (أ₁،…،أ_n) وتوزيع الاحتمالية G الذي يعين الاحتمالات لهم. G هو توزيع احتمالي محدد عبر Θ ولكن هناك العديد من الآخرين. عملية Dirichlet على Θ النماذج بالضبط هذا ؛ هو توزيع على جميع التوزيعات الاحتمالية الممكنة على الفضاء Θ. معلمة عملية Dirichlet مع G₀ الوظيفة الأساسية ومعلمة تركيز α. يمكننا القول أن G يتم توزيعه وفقًا لـ DP مع المعلمات α و G₀ إذا كان التوزيع المشترك للاحتمالات التي يعينها G لأقسام Θ يتبع توزيع Dirichlet. بدلاً من ذلك ، يمكننا القول أن الاحتمالات التي يعينها G لأي قسم محدود من Θ يتبع توزيع Dirichlet.

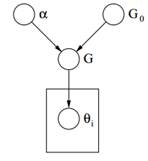
الشكل 2: نموذج رسومي لعملية Dirichlet

أخيرا أعلاه يمكننا أن نرى نموذج رسومي لموانئ دبي. يجب أن نلاحظ أن α هي معلمة مفرطة العددية ، G₀ هو التوزيع الأساسي لـ DP ، G وهو توزيع عشوائي على مساحة المعلمة Θ التي تم أخذ عينات منها من DP والتي تحدد الاحتمالات للمعلمات و θ_i هو ناقل معلمات مستمد من التوزيع G وهو عنصر Θ space.

2. عمليات Dirichlet الخلفية

تمت مناقشة عمليات Dirichlet الخلفية من قبل فيرغسون. نبدأ برسم مقياس الاحتمالية العشوائية G من عملية Dirichlet ، . بما أن G هو توزيع احتمالي على مدى Θ يمكننا أيضًا أخذ عينات من هذا التوزيع واستخلاص عينات مستقلة موزعة متطابقة θ₁، ... ، θ_n ~ G. نظرًا لأن السحوبات من عملية Dirichlet هي توزيعات منفصلة ، يمكننا تمثيلها أين هو تدوين قصير لـ وهي دالة دلتا تأخذ 1 إذا و 0 في مكان آخر. أحد الآثار المثيرة للاهتمام هو أنه بما أن G يتم تعريفه بهذه الطريقة ، فهناك احتمال إيجابي لعينات مختلفة لها نفس القيمة . كما سنرى لاحقًا ، يؤدي هذا إلى إنشاء تأثير تجميعي يمكن استخدامه لإجراء تحليل الكتلة على مجموعات البيانات.

من خلال استخدام التعريفات والملاحظات أعلاه ، نريد تقدير الخلفية لعملية Dirichlet بالنظر إلى العينات θ. ومع ذلك لأننا نعرف ذلك و باستخدام قواعد Bayes والاقتران بين Dirichlet و Multinomial لدينا ذلك و .

المعادلة 1: عملية Dirichlet الخلفية

هذه الخاصية مهمة للغاية ويتم استخدامها من قبل تمثيلات DP المختلفة.

3. تمثيلات عملية Dirichlet

في المقاطع السابقة حددنا عملية Dirichlet وقدمنا ​​نموذجها النظري. أحد الأسئلة المهمة التي يجب أن نجيب عليها هو كيف نعرف أن مثل هذا الشيء موجود وكيف يمكننا بناء وتمثيل عملية Dirichlet.

تم توفير المؤشرات الأولى للوجود من قبل فيرغسون الذين استخدموا نظرية كولموجوروف لاتساق الاتساق ، أعطوا تعريفًا لعملية Dirichlet ووصفوا عملية Dirichlet الخلفية. مواصلة بحثه ، بلاكويل وماكوين استخدم نظرية دي فينيتي لإثبات وجود مثل هذا الإجراء الاحتمالي العشوائي وأدخل مخطط جرة بلاكويل-ماكوين الذي يلبي خصائص عملية ديريتشليت. في عام 1994 سيثرمان قدم طريقة بسيطة ومباشرة إضافية لبناء موانئ دبي من خلال تقديم بناء كسر العصا. وأخيرا تم تقديم تمثيل آخر من قبل ألدوس الذين قدموا عملية المطاعم الصينية كطريقة فعالة لبناء عملية Dirichlet.

إن التمثيلات المختلفة لعملية Dirichlet متكافئة رياضياً لكن صياغتها تختلف لأنها تدرس المشكلة من وجهات نظر مختلفة. نقدم فيما يلي أكثر التوضيحات شيوعًا الموجودة في الأدبيات ونركز على عملية المطاعم الصينية التي توفر طريقة بسيطة وفعالة حسابيًا لإنشاء خوارزميات الاستدلال لعملية Dirichlet.

3.1 مخطط جرة بلاكويل-ماكوين

يمكن استخدام مخطط Blackwell-MacQueen urn لتمثيل عملية Dirichlet وتم تقديمه من قبل بلاكويل وماكوين. وهو يعتمد على مخطط Pólya urn الذي يمكن اعتباره النموذج المعاكس لأخذ العينات دون استبدال. في مخطط Pólya urn نفترض أن لدينا جرة غير شفافة تحتوي على كرات ملونة ونرسم كرات بشكل عشوائي. عندما نرسم كرة ، نلاحظ لونها ، نعيدها إلى الجرة ونضيف كرة إضافية من نفس اللون. يتم استخدام مخطط مماثل من قبل Blackwell و MacQueen لبناء عملية Dirichlet.

ينتج هذا المخطط تسلسل θ₁θ₂، ... مع الاحتمالات الشرطية . في هذا المخطط نفترض أن G₀ هو توزيع على الألوان وكل θ_n يمثل لون الكرة الموضوعة في الجرة. ال خوارزمية هو كما يلي:

· نبدأ بجرة فارغة.

· مع احتمال يتناسب مع α نرسم ونضيف كرة من هذا اللون في الجرة.

· مع احتمال يتناسب مع n-1 ، نرسم كرة عشوائية من الجرة ، ونلاحظ لونها ، ونعيدها إلى الجرة ونضيف كرة إضافية من نفس اللون في الجرة.

بدأنا سابقًا بعملية Dirichlet واشتقنا مخطط Blackwell-MacQueen. لنبدأ الآن بشكل عكسي من مخطط Blackwell-MacQueen واشتقاق DP. منذ θ_i تم رسمها بطريقة عكسية من G ، وسيكون توزيعها المشترك ثابتًا في أي تبديلات محدودة وبالتالي يمكن استبدالها. وبالتالي ، باستخدام نظرية دي فينيتي ، يجب أن يكون هناك توزيع على التدابير لجعلها معرّفة وهذا التوزيع هو عملية ديريتشليت. ونتيجة لذلك ، نثبت أن مخطط Blackwell-MacQueen urn هو تمثيل لـ DP ويمنحنا طريقة ملموسة لبناءه. كما سنرى لاحقًا ، فإن هذا المخطط يعادل رياضيًا عملية المطاعم الصينية.

3.2 بناء كسر العصا

يعتبر البناء الذي يكسر العصا طريقة بديلة لتمثيل عملية Dirichlet التي تم تقديمها من قبل سيثرمان. إنها طريقة بناءة لتشكيل توزيع واستخدامات بعد القياس: نفترض أن لدينا عصا طولها 1 ، نكسرها في الموضع β₁ ونحن نعين π₁ يساوي طول جزء العصا الذي كسرناه. نكرر نفس العملية للحصول على π₂π₃، ... إلخ ؛ نظرًا للطريقة التي يتم بها تعريف هذا المخطط ، يمكننا الاستمرار في القيام بذلك مرات لا حصر لها.

بناء على ما سبق π_k يمكن أن يكون على غرار ، حيث بينما كما في المخططات السابقة ، the يتم أخذ عينات θ مباشرة من التوزيع الأساسي . وبالتالي يمكن كتابة توزيع G كمجموع من وظائف دلتا المرجحة بـ π_k الاحتمالات التي تساوي . وبالتالي يمنحنا البناء الذي يكسر العصا طريقة بسيطة وبديهية لإنشاء عملية Dirichlet.

3.3 عملية المطعم الصيني

عملية المطاعم الصينية ، التي قدمتها ألدوس، هي طريقة فعالة أخرى لتمثيل عملية Dirichlet ويمكن ربطها مباشرة بمخطط Blackwell-MacQueen urn. يستخدم هذا المخطط بعد القياس: نفترض أن هناك مطعم صيني مع طاولات لا نهائية. عند دخول العملاء إلى المطعم ، يجلسون بشكل عشوائي على أي من الطاولات المشغولة أو يختارون الجلوس إلى أول طاولة فارغة متاحة.

يحدد CRP التوزيع على مساحة أقسام الأعداد الصحيحة الموجبة. نبدأ بالرسم θ₁،… θ_n من مخطط جرة بلاكويل-ماكوين. كما ناقشنا في المقاطع السابقة ، نتوقع أن نرى تأثير التجميع وبالتالي فإن العدد الإجمالي للقيم الفريدة k سيكون أقل بكثير من n. وهكذا يحدد هذا تقسيم المجموعة {1,2،1,2،…، n} في مجموعات k. ونتيجة لذلك ، فإن الرسم من مخطط Blackwell-MacQueen urn يؤدي إلى تقسيم عشوائي لمجموعة {XNUMX،XNUMX،…، n}. هذا المطعم الصيني هو السبب التوزيع على الأقسام. الخوارزمية هي على النحو التالي:

· نبدأ بمطعم فارغ.

· و1^st يجلس العميل دائمًا على 1^st جدول

· ن + 1^th العميل لديه خياران:

o اجلس على الطاولة الأولى غير المشغولة باحتمال

o الجلوس على أي من الجداول المحتلة مع احتمال
أين هو عدد الأشخاص الجالسين على تلك الطاولة

حيث α هي قيمة التشتت لـ DP و n هي إجمالي عدد العملاء في المطعم في وقت معين. المتغير الكامن z_i يخزن رقم جدول i^th العميل ويأخذ القيم من 1 إلى k_n حيث ك_n هو العدد الإجمالي للطاولات المشغولة عندما يكون n العملاء في المطعم. يجب أن نلاحظ أن ك_n ستكون دائمًا أقل أو تساوي n وفي المتوسط ​​تكون على وشك . أخيرا يجب أن نلاحظ أن احتمال ترتيب الجدول هو ثابت على التباديل. وبالتالي فإن z_i قابل للاستبدال مما يعني أن الجداول التي لها نفس حجم العملاء لها نفس الاحتمال.

ترتبط عملية المطاعم الصينية ارتباطًا قويًا بمخطط Pólya urn وعملية Dirichlet. CRP هو طريقة لتحديد أ التوزيع على الأقسام (تخصيصات الجدول) للنقاط n ويمكن استخدامها كسابق على مساحة المتغير الكامن z_i التي يحدد تعيينات الكتلة. تعادل CRP نظام ólya urn مع اختلاف فقط في أنه لا يعين معلمات لكل جدول / مجموعة. توجو من CRP إلى مخطط جرة Pólya نرسم لجميع الجداول ك = 1,2،XNUMX ... ثم لكل س_i الذي تم تجميعه في الجدول z_i تعيين . بمعنى آخر ، قم بتعيين x الجديد_i المعلمة θ من الجدول. أخيرا منذ ذلك الحين لا يمكننا التكليف θ إلى الجداول اللانهائية من البداية ، يمكننا فقط تعيين جدول جديد θ في كل مرة يجلس شخص ما على طاولة جديدة. نظرًا لكل ما سبق ، يمكن أن يساعدنا CRP في إنشاء خوارزميات فعالة حسابيًا لإجراء تحليل الكتلة على مجموعات البيانات.

في هذا المنشور ، ناقشنا عملية Dirichlet وطرق عديدة لبناءها. سنستخدم الأفكار المذكورة أعلاه في المقالة التالية. سنقدم نموذج Dirichlet Mixture Model وسنستخدم تمثيل المطعم الصيني من أجل إنشاء عملية Dirichlet وتحليل التشكيل. إذا فاتتك نقاط قليلة فلا تقلق حيث ستصبح الأمور أكثر وضوحًا مع المادتين التاليتين.

اتمنى ان تجد هذا المنشور ممتع إذا فعلت ذلك ، خذ لحظة لمشاركتها على Facebook و Twitter. 🙂