এআই টেক ফ্লাইটের সাথে উপবৃত্তাকার বক্ররেখা 'মর্মুরেশনস' পাওয়া গেছে | কোয়ান্টা ম্যাগাজিন

উপবৃত্তাকার বক্ররেখাগুলি আধুনিক গণিতের আরও বিভ্রান্তিকর বস্তুগুলির মধ্যে একটি। এগুলি জটিল বলে মনে হয় না, তবে তারা গণিতের মধ্যে একটি এক্সপ্রেসওয়ে তৈরি করে যা অনেক লোক উচ্চ বিদ্যালয়ে শেখে এবং গণিত নিয়ে গবেষণা করে। এগুলি 1990-এর দশকে ফার্মাটের শেষ উপপাদ্যের পালিত প্রমাণ অ্যান্ড্রু ওয়াইলসের কেন্দ্রীয় ছিল। তারা আধুনিক ক্রিপ্টোগ্রাফির মূল হাতিয়ার। এবং 2000 সালে, ক্লে ম্যাথমেটিক্স ইনস্টিটিউটের নাম একটি পরিসংখ্যান সম্পর্কে অনুমান উপবৃত্তাকার বক্ররেখা সাতটি "সহস্রাব্দ পুরস্কার সমস্যা" এর মধ্যে একটি, যার প্রত্যেকটির সমাধানের জন্য $1 মিলিয়ন পুরস্কার রয়েছে। যে অনুমান, প্রথম দ্বারা ventured ব্রায়ান বার্চ এবং পিটার সুইনারটন-ডায়ার 1960-এর দশকে, এখনও প্রমাণিত হয়নি।

উপবৃত্তাকার বক্ররেখা বোঝা একটি উচ্চ-প্রচেষ্টা যা গণিতের কেন্দ্রীয় বিষয়। তাই 2022 সালে, যখন একটি ট্রান্সঅ্যাটলান্টিক সহযোগিতা পরিসংখ্যানগত কৌশল এবং কৃত্রিম বুদ্ধিমত্তা ব্যবহার করে উপবৃত্তাকার বক্ররেখায় সম্পূর্ণ অপ্রত্যাশিত নিদর্শনগুলি আবিষ্কার করে, এটি একটি স্বাগত ছিল, যদি অপ্রত্যাশিত হয়, অবদান। "মেশিন লার্নিং আমাদের দোরগোড়ায় আকর্ষণীয় কিছু নিয়ে আসার আগে এটি সময়ের ব্যাপার ছিল," বলেন পিটার সারনাক, ইনস্টিটিউট ফর অ্যাডভান্সড স্টাডি এবং প্রিন্সটন ইউনিভার্সিটির একজন গণিতবিদ। প্রাথমিকভাবে, কেউ ব্যাখ্যা করতে পারেনি কেন নতুন আবিষ্কৃত নিদর্শন বিদ্যমান। তারপর থেকে, সাম্প্রতিক গবেষণাপত্রের একটি সিরিজে, গণিতবিদরা নিদর্শনগুলির পিছনের কারণগুলি আনলক করতে শুরু করেছেন, যাকে "মর্ম্যুরেশন" বলে ডাকা হয়েছে ফ্লাকিং স্টারলিংসের তরল আকারের সাথে তাদের সাদৃশ্যের জন্য, এবং প্রমাণ করতে শুরু করেছেন যে সেগুলি কেবল নির্দিষ্ট ক্ষেত্রেই ঘটবে না। উদাহরণ 2022 সালে পরীক্ষা করা হয়েছে, কিন্তু উপবৃত্তাকার বক্ররেখায় আরও সাধারণভাবে।

উপবৃত্তাকার হওয়ার গুরুত্ব

সেই প্যাটার্নগুলি কী তা বোঝার জন্য, উপবৃত্তাকার বক্ররেখাগুলি কী এবং গণিতবিদরা কীভাবে সেগুলিকে শ্রেণীবদ্ধ করেন সে সম্পর্কে আমাদের একটু ভিত্তি স্থাপন করতে হবে।

একটি উপবৃত্তাকার বক্ররেখা একটি ভেরিয়েবলের বর্গকে সম্পর্কিত করে, সাধারণত লেখা হয় y, অন্যের তৃতীয় শক্তিতে, সাধারণত লেখা হয় x: y² = x³ + Ax + B, কিছু জোড়া সংখ্যার জন্য A এবং B, যতক্ষন পর্যন্ত না A এবং B কয়েকটি সহজ শর্ত পূরণ করুন। এই সমীকরণটি একটি বক্ররেখা সংজ্ঞায়িত করে যা সমতলে গ্রাফ করা যেতে পারে, যেমনটি নীচে দেখানো হয়েছে। (নামের মিল থাকা সত্ত্বেও, একটি উপবৃত্ত একটি উপবৃত্তাকার বক্ররেখা নয়।)

যদিও সরল চেহারার, উপবৃত্তাকার বক্ররেখাগুলি সংখ্যা তাত্ত্বিকদের জন্য অবিশ্বাস্যভাবে শক্তিশালী হাতিয়ার হয়ে উঠেছে - গণিতবিদ যারা পূর্ণসংখ্যার নিদর্শনগুলি সন্ধান করেন। পরিবর্তে চলক লেট x এবং y সমস্ত সংখ্যার উপর পরিসীমা, গণিতবিদরা তাদের বিভিন্ন সংখ্যা পদ্ধতিতে সীমাবদ্ধ রাখতে পছন্দ করেন, যাকে তারা একটি বক্ররেখার সংজ্ঞা "ওভার" একটি প্রদত্ত সংখ্যা সিস্টেম বলে। উপবৃত্তাকার বক্ররেখাগুলি মূলদ সংখ্যাগুলির মধ্যে সীমাবদ্ধ - যে সংখ্যাগুলি ভগ্নাংশ হিসাবে লেখা যেতে পারে - বিশেষভাবে কার্যকর। "বাস্তব বা জটিল সংখ্যার উপর উপবৃত্তাকার বক্ররেখা বেশ বিরক্তিকর," সারনাক বলেন। "এটি কেবলমাত্র মূলদ সংখ্যা যা গভীর।"

এখানে একটি উপায় যে সত্য. যদি আপনি একটি উপবৃত্তাকার বক্ররেখার দুটি মূলদ বিন্দুর মধ্যে একটি সরল রেখা আঁকেন, তাহলে সেই রেখাটি আবার বক্ররেখাকে ছেদ করার জায়গাটিও যুক্তিযুক্ত হবে। আপনি একটি উপবৃত্তাকার বক্ররেখায় "সংযোজন" সংজ্ঞায়িত করতে সেই সত্যটি ব্যবহার করতে পারেন, যেমনটি নীচে দেখানো হয়েছে।

মধ্যে একটি লাইন আঁকুন P এবং Q. সেই রেখাটি একটি তৃতীয় বিন্দুতে বক্ররেখাকে ছেদ করবে, R. (গণিতবিদদের একটি বিশেষ কৌশল আছে যে ক্ষেত্রে রেখাটি "অসীম বিন্দুতে" যোগ করে বক্ররেখাকে ছেদ করে না।) এর প্রতিফলন R সম্মুখীন x-অক্ষ হল আপনার যোগফল P + Q. এই সংযোজন ক্রিয়াকলাপের সাথে একসাথে, বক্ররেখার সমস্ত সমাধান একটি গাণিতিক বস্তু গঠন করে যাকে গ্রুপ বলা হয়।

গণিতবিদরা একটি বক্ররেখার "র্যাঙ্ক" সংজ্ঞায়িত করতে এটি ব্যবহার করেন। দ্য একটি বক্ররেখা এটির যৌক্তিক সমাধানের সংখ্যার সাথে সম্পর্কিত। র্যাঙ্ক 0 বক্ররেখার একটি সীমিত সংখ্যক সমাধান রয়েছে। উচ্চতর র‍্যাঙ্ক সহ বক্ররেখার অসীম সংখ্যক সমাধান রয়েছে যার যোগ ক্রিয়াকলাপ ব্যবহার করে একে অপরের সাথে সম্পর্কটি র্যাঙ্ক দ্বারা বর্ণনা করা হয়েছে।

পদমর্যাদা ভালোভাবে বোঝা যায় না; গণিতবিদদের সর্বদা তাদের গণনা করার একটি উপায় থাকে না এবং তারা কতটা বড় হতে পারে তা জানেন না। (একটি নির্দিষ্ট বক্ররেখার জন্য সবচেয়ে বড় সঠিক র‌্যাঙ্ক হল 20)

উপবৃত্তাকার বক্ররেখারও মৌলিক সংখ্যার সাথে অনেক সম্পর্ক রয়েছে, যেগুলি শুধুমাত্র 1 এবং নিজেদের দ্বারা বিভাজ্য। বিশেষ করে, গণিতবিদরা সীমিত ক্ষেত্রগুলির উপর বক্ররেখাগুলি দেখেন - চক্রীয় গাণিতিকের সিস্টেম যা প্রতিটি মৌলিক সংখ্যার জন্য সংজ্ঞায়িত করা হয়। একটি সীমিত ক্ষেত্র হল একটি ঘড়ির মতো যার ঘন্টা সংখ্যা প্রাইমের সমান: আপনি যদি ঊর্ধ্বমুখী গণনা করতে থাকেন তবে সংখ্যাগুলি আবার শুরু হবে। 7 এর জন্য সসীম ক্ষেত্রে, উদাহরণস্বরূপ, 5 যোগ 2 সমান শূন্য, এবং 5 যোগ 3 সমান 1।

একটি উপবৃত্তাকার বক্ররেখায় সংখ্যার একটি যুক্ত ক্রম থাকে, যাকে বলা হয় a_p, যা প্রাইম দ্বারা সংজ্ঞায়িত সসীম ক্ষেত্রের বক্ররেখার সাথে সমাধানের সংখ্যার সাথে সম্পর্কিত p। আরও ছোট a_p আরো সমাধান মানে; একটি বড় a_p মানে কম সমাধান। যদিও র‌্যাঙ্ক হিসাব করা কঠিন, ক্রম a_p অনেক সহজ।

প্রথম কম্পিউটারগুলির একটিতে করা অসংখ্য গণনার ভিত্তিতে, বার্চ এবং সুইনারটন-ডায়ার একটি উপবৃত্তাকার বক্ররেখার ক্রম এবং অনুক্রমের মধ্যে একটি সম্পর্ক অনুমান করেছিলেন a_p. যে কেউ প্রমাণ করতে পারে যে তারা সঠিক ছিল তারা এক মিলিয়ন ডলার এবং গাণিতিক অমরত্ব জিততে পারে।

একটি আশ্চর্য প্যাটার্ন আবির্ভূত

মহামারী শুরু হওয়ার পর, ইয়াং-হুই হি, লন্ডন ইনস্টিটিউট ফর ম্যাথমেটিকাল সায়েন্সেস-এর একজন গবেষক, কিছু নতুন চ্যালেঞ্জ নেওয়ার সিদ্ধান্ত নিয়েছেন। তিনি কলেজে পদার্থবিজ্ঞানের প্রধান ছিলেন এবং ম্যাসাচুসেটস ইনস্টিটিউট অফ টেকনোলজি থেকে গাণিতিক পদার্থবিদ্যায় ডক্টরেট ডিগ্রি অর্জন করেছিলেন। কিন্তু তিনি সংখ্যা তত্ত্বের প্রতি ক্রমবর্ধমান আগ্রহী ছিলেন এবং কৃত্রিম বুদ্ধিমত্তার ক্রমবর্ধমান ক্ষমতার পরিপ্রেক্ষিতে তিনি ভেবেছিলেন যে তিনি সংখ্যায় অপ্রত্যাশিত নিদর্শন খুঁজে বের করার জন্য একটি হাতিয়ার হিসাবে AI ব্যবহার করার চেষ্টা করবেন। (তিনি ইতিমধ্যেই ছিলেন মেশিন লার্নিং ব্যবহার করে শ্রেণিভুক্ত করতে ক্যালাবি-ইয়াউ বহুগুণ, গাণিতিক কাঠামো যা স্ট্রিং তত্ত্বে ব্যাপকভাবে ব্যবহৃত হয়।)

2020 সালের আগস্টে, মহামারীটি গভীর হওয়ার সাথে সাথে নটিংহাম বিশ্ববিদ্যালয় তাকে একটি অনুষ্ঠানের জন্য আমন্ত্রণ জানায় অনলাইন আলাপ. তিনি তার অগ্রগতি সম্পর্কে এবং নতুন গণিত উদ্ঘাটনের জন্য মেশিন লার্নিং ব্যবহার করার সম্ভাবনা সম্পর্কে হতাশাবাদী ছিলেন। "তার বর্ণনাটি ছিল যে সংখ্যা তত্ত্বটি কঠিন ছিল কারণ আপনি সংখ্যা তত্ত্বের জিনিসগুলি মেশিনে শিখতে পারেননি," বলেন টমাস অলিভার, ওয়েস্টমিনস্টার বিশ্ববিদ্যালয়ের একজন গণিতবিদ যিনি দর্শকদের মধ্যে ছিলেন। তিনি যেমন মনে করেন, “আমি কিছু খুঁজে পাইনি কারণ আমি একজন বিশেষজ্ঞ ছিলাম না। আমি এটি দেখার জন্য সঠিক জিনিসগুলিও ব্যবহার করছিলাম না।"

অলিভার এবং কিউ-হোয়ান লি, কানেকটিকাট বিশ্ববিদ্যালয়ের একজন গণিতবিদ, তাঁর সাথে কাজ শুরু করেন। অলিভার বলেন, "আমরা গণিতকে গুরুত্ব সহকারে অধ্যয়ন করার পরিবর্তে শুধুমাত্র মেশিন লার্নিং কী তা জানার জন্য এটি করার সিদ্ধান্ত নিয়েছি।" "কিন্তু আমরা দ্রুত খুঁজে পেয়েছি যে আপনি মেশিনে অনেক কিছু শিখতে পারেন।"

অলিভার এবং লি পরামর্শ দিয়েছিলেন যে তিনি পরীক্ষা করার জন্য তার কৌশল প্রয়োগ করেন L-ফাংশন, অনুক্রমের মাধ্যমে উপবৃত্তাকার বক্ররেখার সাথে ঘনিষ্ঠভাবে সম্পর্কিত অসীম সিরিজ a_p. তারা উপবৃত্তাকার বক্ররেখা এবং তাদের সম্পর্কিত একটি অনলাইন ডাটাবেস ব্যবহার করতে পারে L- ফাংশন বলা হয় LMFDB তাদের মেশিন লার্নিং ক্লাসিফায়ারদের প্রশিক্ষণ দিতে। সেই সময়ে ডাটাবেসের যৌক্তিকতার উপরে 3 মিলিয়ন উপবৃত্তাকার বক্ররেখা ছিল। 2020 সালের অক্টোবরের মধ্যে, তারা ছিল একটি কাগজ যে তথ্য থেকে সংগৃহীত ব্যবহার করা হয়েছে L- উপবৃত্তাকার বক্ররেখার একটি নির্দিষ্ট সম্পত্তি ভবিষ্যদ্বাণী করার ফাংশন। নভেম্বরে তারা ভাগ করেছে অন্য কাগজ যেটি সংখ্যা তত্ত্বে অন্যান্য বস্তুকে শ্রেণিবদ্ধ করতে মেশিন লার্নিং ব্যবহার করে। ডিসেম্বরের মধ্যে, তারা সক্ষম হয়েছিল উপবৃত্তাকার বক্ররেখার পূর্বাভাস উচ্চ নির্ভুলতা সঙ্গে।

কিন্তু তারা নিশ্চিত ছিল না কেন তাদের মেশিন লার্নিং অ্যালগরিদম এত ভালো কাজ করছে। লি তার স্নাতক ছাত্র আলেক্সি পোজডনিয়াকভকে জিজ্ঞাসা করেছিলেন যে তিনি কী ঘটছে তা বুঝতে পারেন কিনা। এটি যেমন ঘটে, LMFDB কন্ডাক্টর নামক একটি পরিমাণ অনুসারে উপবৃত্তাকার বক্ররেখাগুলিকে সাজায়, যা প্রাইমগুলি সম্পর্কে তথ্য সংক্ষিপ্ত করে যার জন্য একটি বক্ররেখা ভাল আচরণ করতে ব্যর্থ হয়। তাই Pozdnyakov একই সাথে একই কন্ডাক্টর সহ বড় সংখ্যক বক্ররেখা দেখার চেষ্টা করেছেন — বলুন, 7,500 থেকে 10,000 এর মধ্যে কন্ডাক্টর সহ সমস্ত বক্ররেখা।

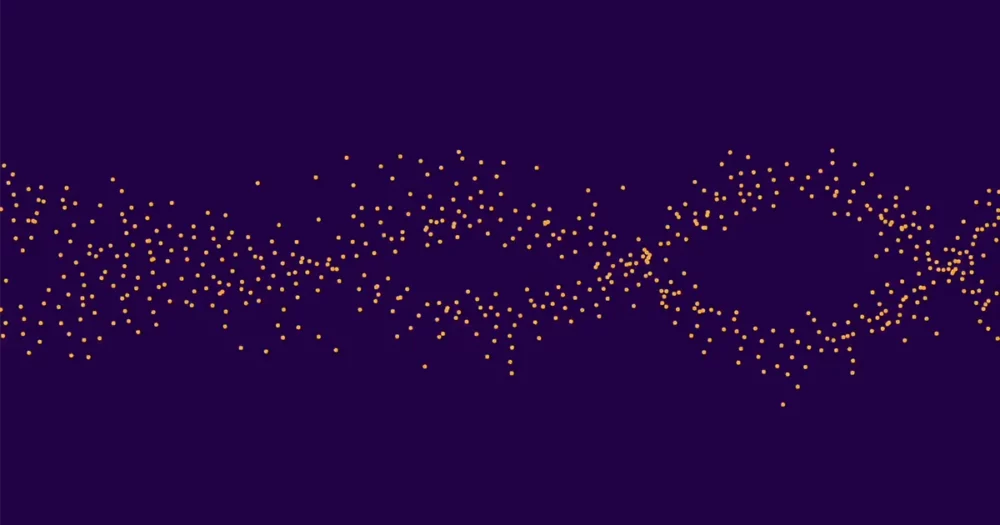
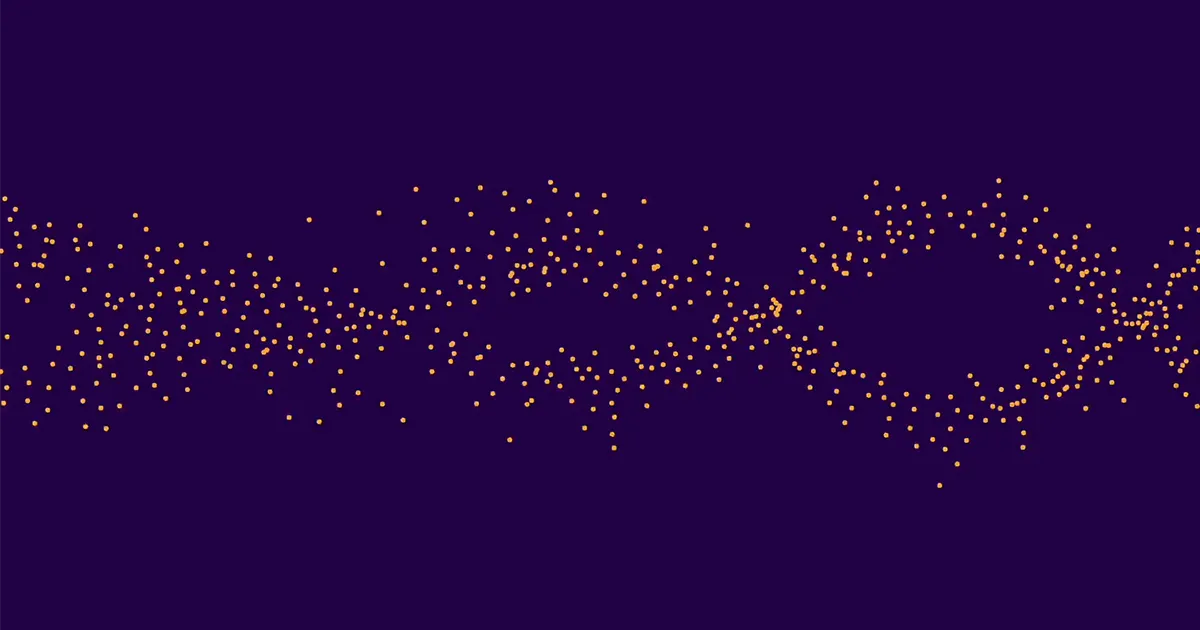
এটি মোট প্রায় 10,000 বক্ররেখার পরিমাণ। এর মধ্যে প্রায় অর্ধেকের র‍্যাঙ্ক ছিল 0, এবং অর্ধেক র‍্যাঙ্ক ছিল 1। (উচ্চ র‍্যাঙ্কগুলি অত্যন্ত বিরল।) তারপর তিনি এর মান গড় করলেন a_p সমস্ত র্যাঙ্ক 0 বক্ররেখার জন্য, আলাদাভাবে গড় a_p সমস্ত র্যাঙ্ক 1 বক্ররেখার জন্য, এবং ফলাফলগুলি প্লট করেছে৷ বিন্দুর দুটি সেট দুটি স্বতন্ত্র, সহজে বোঝা যায় এমন তরঙ্গ তৈরি করেছে। এই কারণেই মেশিন লার্নিং ক্লাসিফায়াররা সঠিকভাবে নির্দিষ্ট বক্ররেখার স্থান নির্ধারণ করতে সক্ষম হয়েছিল।

"প্রথমে আমি খুশি হয়েছিলাম যে আমি অ্যাসাইনমেন্টটি সম্পূর্ণ করতে পেরেছি," পোজডনিয়াকভ বলেছিলেন। "কিন্তু কিউ-হোয়ান অবিলম্বে স্বীকার করেছিলেন যে এই প্যাটার্নটি আশ্চর্যজনক ছিল, এবং তখনই এটি সত্যিই উত্তেজনাপূর্ণ হয়ে ওঠে।"

লি এবং অলিভার মুগ্ধ হয়েছিল। "অ্যালেক্সি আমাদের ছবিটি দেখিয়েছিল, এবং আমি বলেছিলাম যে পাখিরা যা করে তা দেখে মনে হচ্ছে," অলিভার বলেছিলেন। "এবং তারপর কিউ-হোয়ান এটির দিকে তাকালো এবং বলল এটাকে বচসা বলা হয়, এবং তারপর ইয়াং বললো আমাদের কাগজটা কল করা উচিত'উপবৃত্তাকার বক্ররেখার বচসা। ' "

তারা এপ্রিল 2022-এ তাদের কাগজ আপলোড করেছিল এবং মুষ্টিমেয় অন্যান্য গণিতবিদদের কাছে এটি ফরোয়ার্ড করেছিল, নার্ভাসভাবে আশা করে যে তাদের তথাকথিত "আবিষ্কার" সুপরিচিত ছিল। অলিভার বলেছিলেন যে সম্পর্কটি এতটাই দৃশ্যমান ছিল যে এটি অনেক আগেই লক্ষ্য করা উচিত ছিল।

প্রায় অবিলম্বে, প্রিপ্রিন্ট আগ্রহ অর্জন করে, বিশেষ করে থেকে অ্যান্ড্রু সুদারল্যান্ড, MIT-এর একজন গবেষণা বিজ্ঞানী যিনি LMFDB-এর ব্যবস্থাপনা সম্পাদকদের একজন। সাদারল্যান্ড বুঝতে পেরেছিলেন যে 3 মিলিয়ন উপবৃত্তাকার বক্ররেখা তার উদ্দেশ্যে যথেষ্ট নয়। বচসাগুলি কতটা শক্তিশালী তা দেখতে তিনি অনেক বড় কন্ডাক্টর রেঞ্জের দিকে তাকাতে চেয়েছিলেন। তিনি প্রায় 150 মিলিয়ন উপবৃত্তাকার বক্ররেখার আরেকটি বিশাল ভান্ডার থেকে ডেটা টেনে আনেন। এখনও অসন্তুষ্ট, তিনি তারপর 300 মিলিয়ন বক্ররেখা সহ একটি ভিন্ন সংগ্রহস্থল থেকে ডেটা টেনে আনেন।

"কিন্তু এমনকি সেগুলিও যথেষ্ট ছিল না, তাই আমি আসলে এক বিলিয়নের বেশি উপবৃত্তাকার বক্ররেখার একটি নতুন ডেটা সেট গণনা করেছি, এবং এটিই আমি সত্যিই উচ্চ-রেজোলিউশনের ছবিগুলি গণনা করতে ব্যবহার করেছি," সাদারল্যান্ড বলেছিলেন। বকবক দেখায় যে তিনি এক সময়ে গড়ে 15,000 উপবৃত্তাকার বক্ররেখা করেছেন নাকি এক সময়ে এক মিলিয়ন। বৃহত্তর এবং বৃহত্তর মৌলিক সংখ্যার উপর বক্ররেখার দিকে তাকালেও আকৃতি একই ছিল, একটি ঘটনা যাকে বলা হয় স্কেল ইনভেরিয়েন্স। সাদারল্যান্ড আরও বুঝতে পেরেছিলেন যে বচনগুলি উপবৃত্তাকার বক্ররেখার জন্য অনন্য নয়, বরং আরও সাধারণভাবে দেখা যায় L- ফাংশন। সে লিখেছিলো একটি চিঠি তার ফলাফলের সারসংক্ষেপ এবং এটি সরনাকের কাছে পাঠিয়েছে এবং মাইকেল রুবিনস্টাইন ওয়াটারলু বিশ্ববিদ্যালয়ে।

"যদি এটির জন্য একটি পরিচিত ব্যাখ্যা থাকে তবে আমি আশা করি আপনি এটি জানতে পারবেন," সাদারল্যান্ড লিখেছেন।

তারা করেনি।

প্যাটার্ন ব্যাখ্যা

লি, তিনি এবং অলিভার 2023 সালের আগস্টে ব্রাউন ইউনিভার্সিটির ইনস্টিটিউট ফর কম্পিউটেশনাল অ্যান্ড এক্সপেরিমেন্টাল রিসার্চ ইন ম্যাথমেটিক্সে (ICERM) একটি কর্মশালার আয়োজন করেছিলেন। সারনাক এবং রুবিনস্টেইন এসেছিলেন, যেমনটি এসেছিলেন সারনাকের ছাত্র নিনা জুব্রিলিনা.

জুব্রিলিনা তার গবেষনা পেশ করেন মুর্মুরেশন প্যাটার্নে মডুলার ফর্ম, বিশেষ জটিল ফাংশন যা, উপবৃত্তাকার বক্ররেখার মত, যুক্ত আছে L- ফাংশন। বৃহৎ কন্ডাক্টর সহ মডুলার আকারে, বচসাগুলি একটি স্পষ্ট কিন্তু বিচ্ছুরিত প্যাটার্ন গঠনের পরিবর্তে একটি তীব্রভাবে সংজ্ঞায়িত বক্ররেখায় রূপান্তরিত হয়। ভিতরে একটি কাগজ 11 অক্টোবর, 2023-এ পোস্ট করা, জুব্রিলিনা প্রমাণ করেছেন যে এই ধরনের বচসা তার আবিষ্কৃত একটি সুস্পষ্ট সূত্র অনুসরণ করে।

“নিনার বড় প্রাপ্তি হল যে তাকে এর জন্য একটি সূত্র দেওয়া হয়েছে; আমি এটাকে জুব্রিলিনা মুর্মুরেশন ডেনসিটি ফর্মুলা বলি,” সারনাক বলেন। "খুব পরিশীলিত গণিত ব্যবহার করে, তিনি একটি সঠিক সূত্র প্রমাণ করেছেন যা ডেটার সাথে পুরোপুরি ফিট করে।"

তার সূত্রটি জটিল, কিন্তু সারনাক এটিকে একটি গুরুত্বপূর্ণ নতুন ধরনের ফাংশন হিসাবে অভিহিত করেছেন, যা আলোকবিজ্ঞান থেকে কোয়ান্টাম মেকানিক্স পর্যন্ত পদার্থবিদ্যার বিভিন্ন প্রসঙ্গে ব্যবহৃত ডিফারেনশিয়াল সমীকরণের সমাধানকে সংজ্ঞায়িত করে বাতাসযুক্ত ফাংশনের সাথে তুলনীয়।

জুব্রিলিনার সূত্রটি প্রথম হলেও অন্যরা অনুসরণ করেছে। "এখন প্রতি সপ্তাহে, একটি নতুন কাগজ বের হয়," সারনাক বলেছিলেন, "প্রধানত জুব্রিলিনার সরঞ্জামগুলি ব্যবহার করে, বচসাগুলির অন্যান্য দিকগুলি ব্যাখ্যা করে।"

জনাথন বোবার, অ্যান্ড্রু বুকার এবং মিন লি ব্রিস্টল বিশ্ববিদ্যালয়ের, একসাথে ডেভিড লোরি-ডুডা আইসিইআরএম-এর, মডুলার আকারে একটি ভিন্ন ধরনের বচসায়ের অস্তিত্ব প্রমাণ করেছে অক্টোবরের আরেকটি কাগজ. এবং কিউ-হোয়ান লি, অলিভার এবং পোজডনিয়াকভ অস্তিত্ব প্রমাণ করেছে ডিরিচলেট অক্ষর নামক বস্তুর মধ্যে বচসা যা ঘনিষ্ঠভাবে সম্পর্কিত L- ফাংশন।

সাদারল্যান্ড ভাগ্যের উল্লেখযোগ্য ডোজ দ্বারা প্রভাবিত হয়েছিলেন যা বকবক আবিষ্কারের দিকে পরিচালিত করেছিল। যদি উপবৃত্তাকার বক্ররেখার ডেটা কন্ডাক্টর দ্বারা আদেশ না করা হত, তবে বচসাগুলি অদৃশ্য হয়ে যেত। "তারা LMFDB থেকে ডেটা নেওয়ার জন্য সৌভাগ্যবান ছিল, যা কন্ডাক্টর অনুসারে আগে থেকে সাজানো হয়েছিল," তিনি বলেছিলেন। "এটি একটি উপবৃত্তাকার বক্ররেখাকে সংশ্লিষ্ট মডুলার ফর্মের সাথে সম্পর্কিত করে, তবে এটি মোটেও সুস্পষ্ট নয়। … দুটি বক্ররেখা যার সমীকরণগুলি খুব একই রকম দেখায় খুব আলাদা কন্ডাক্টর থাকতে পারে।" উদাহরণস্বরূপ, সাদারল্যান্ড এটি উল্লেখ করেছেন y² = x³ - 11x + 6 এর কন্ডাক্টর 17 আছে, কিন্তু বিয়োগ চিহ্নটিকে প্লাস চিহ্নে উল্টানো, y² = x³ + + 11x + 6 এর কন্ডাক্টর 100,736 আছে।

তারপরেও, বচসাগুলি কেবল পজডনিয়াকভের অনভিজ্ঞতার কারণে পাওয়া গেছে। "আমি মনে করি না যে আমরা তাকে ছাড়া এটি খুঁজে পেতাম," অলিভার বলেছিলেন, "কারণ বিশেষজ্ঞরা ঐতিহ্যগতভাবে স্বাভাবিক a_p পরম মান 1। কিন্তু তিনি সেগুলিকে স্বাভাবিক করেননি … তাই দোলনগুলি খুব বড় এবং দৃশ্যমান ছিল।"

এআই অ্যালগরিদমগুলি র্যাঙ্ক অনুসারে উপবৃত্তাকার বক্ররেখাগুলিকে সাজানোর জন্য যে পরিসংখ্যানগত নিদর্শনগুলি ব্যবহার করে তা শত শত মাত্রা সহ একটি প্যারামিটার স্পেসে বিদ্যমান - মানুষের মনের মধ্যে বাছাই করার জন্য অনেক বেশি, অলিভার উল্লেখ করেছেন। কিন্তু যদিও মেশিন লার্নিং লুকানো দোলনগুলি খুঁজে পেয়েছিল, "শুধু পরেই আমরা সেগুলিকে বচসা বলে বুঝতে পেরেছি।"

সম্পাদকের দ্রষ্টব্য: অ্যান্ড্রু সাদারল্যান্ড, কিউ-হোয়ান লি এবং এল-ফাংশন এবং মডুলার ফর্ম ডাটাবেস (LMFDB) সকলেই সিমন্স ফাউন্ডেশন থেকে তহবিল পেয়েছে, যা এই সম্পাদকীয়ভাবে স্বাধীন প্রকাশনাকে অর্থায়ন করে। সিমন্স ফাউন্ডেশন ফান্ডিং সিদ্ধান্ত আমাদের কভারেজের উপর কোন প্রভাব ফেলে না। আরো তথ্য পাওয়া যায় এখানে.