Big O-notation og algoritmeanalyse med Python-eksempler

Introduktion

Der er normalt flere måder at løse problemet på ved hjælp af et computerprogram. For eksempel er der flere måder at sortere elementer i et array - du kan bruge fusion sortere, boble sortering, indsætnings sortering, og så videre. Alle disse algoritmer har deres egne fordele og ulemper, og udviklerens opgave er at veje dem for at være i stand til at vælge den bedste algoritme, der skal bruges i enhver brugssituation. Med andre ord er hovedspørgsmålet, hvilken algoritme der skal bruges til at løse et specifikt problem, når der findes flere løsninger på problemet.

Algoritme analyse refererer til analysen af ​​kompleksiteten af ​​forskellige algoritmer og at finde den mest effektive algoritme til at løse det aktuelle problem. Big-O notation er et statistisk mål, der bruges til at beskrive kompleksiteten af ​​algoritmen.

I denne guide vil vi først tage en kort gennemgang af algoritmeanalyse og derefter tage et dybere kig på Big-O-notationen. Vi vil se, hvordan Big-O-notation kan bruges til at finde algoritmekompleksitet ved hjælp af forskellige Python-funktioner.

Hvorfor er algoritmeanalyse vigtig?

For at forstå, hvorfor algoritmeanalyse er vigtig, vil vi tage hjælp af et simpelt eksempel. Antag, at en leder giver en opgave til to af sine medarbejdere om at designe en algoritme i Python, der beregner fakultetet af et tal, som brugeren indtaster. Algoritmen udviklet af den første medarbejder ser sådan ud:

def fact(n):
    product = 1
    for i in range(n):
        product = product * (i+1)
    return product

print(fact(5))

Bemærk, at algoritmen blot tager et heltal som et argument. Inde i fact() funktion en variabel navngivet product er initialiseret til 1. En løkke udføres fra 1 til n og under hver iteration, værdien i product ganges med tallet, der gentages af løkken, og resultatet gemmes i product variabel igen. Efter at løkken er udført, vil product variablen vil indeholde faktoren.

På samme måde udviklede den anden medarbejder også en algoritme, der beregner et tals fakultet. Den anden medarbejder brugte en rekursiv funktion til at beregne tallets fakultet n:

def fact2(n):
    if n == 0:
        return 1
    else:
        return n * fact2(n-1)

print(fact2(5))

Lederen skal beslutte, hvilken algoritme der skal bruges. For at gøre det har de besluttet at vælge, hvilken algoritme der kører hurtigere. En måde at gøre det på er ved at finde den tid, der kræves til at udføre koden på samme input.

I Jupyter-notesbogen kan du bruge %timeit bogstaveligt efterfulgt af funktionskaldet for at finde den tid, det tager funktionen at udføre:

%timeit fact(50)

Dette vil give os:

9 µs ± 405 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Outputtet siger, at algoritmen tager 9 mikrosekunder (plus/minus 45 nanosekunder) pr. sløjfe.

På samme måde kan vi beregne, hvor lang tid den anden tilgang tager at udføre:

%timeit fact2(50)

Dette vil resultere i:

15.7 µs ± 427 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Den anden algoritme, der involverer rekursion, tager 15 mikrosekunder (plus/minus 427 nanosekunder).

Udførelsestiden viser, at den første algoritme er hurtigere sammenlignet med den anden algoritme, der involverer rekursion. Når man har at gøre med store input, kan præstationsforskellen blive mere markant.

Udførelsestid er dog ikke en god metrik til at måle kompleksiteten af ​​en algoritme, da den afhænger af hardwaren. Der er behov for en mere objektiv kompleksitetsanalyse for en algoritme. Det er her Stor O-notation kommer til at spille.

Algoritmeanalyse med Big-O-notation

Big-O notation angiver forholdet mellem input til algoritmen og de nødvendige trin for at udføre algoritmen. Det er angivet med et stort "O" efterfulgt af en åbnings- og lukkeparentes. Inde i parentesen præsenteres forholdet mellem inputtet og de trin, algoritmen tager ved hjælp af "n".

Det vigtigste er – Big-O er ikke interesseret i en særlig instans, hvor du kører en algoritme, som f.eks fact(50), men snarere, hvor godt gør det skala givet stigende input. Dette er en meget bedre metrik til evaluering end konkret tid til en konkret instans!

Hvis der f.eks. er en lineær sammenhæng mellem inputtet og det trin, algoritmen tager for at fuldføre dens udførelse, vil den anvendte Big-O-notation være O (n). Tilsvarende er Big-O-notationen for kvadratiske funktioner is O(n²).

For at opbygge intuition:

• O (n): kl n=1, 1 skridt er taget. På n=10, tages 10 trin.
• O(n²): kl n=1, 1 skridt er taget. På n=10, tages 100 trin.

At n=1, ville disse to præstere det samme! Dette er en anden grund til, at det er bedre at observere forholdet mellem input og antallet af trin til at behandle det input end blot at evaluere funktioner med nogle konkrete input.

Følgende er nogle af de mest almindelige Big-O-funktioner:

Navn	Stor O
Konstant	O (c)
Lineær	O (n)
Kvadratisk	O(n²)
Cubic	O(n³)
Eksponentiel	O(2ⁿ)
Logaritmisk	O (log (n))
Log Lineær	O(nlog(n))

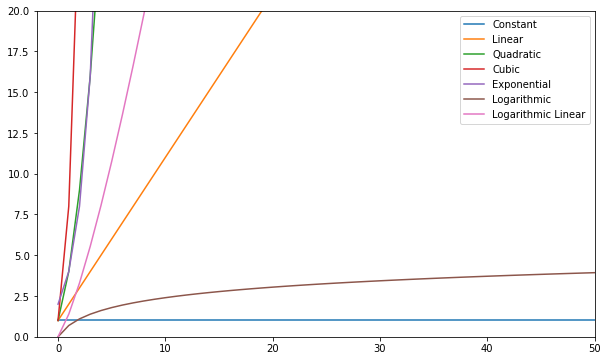
Du kan visualisere disse funktioner og sammenligne dem:

Generelt set – alt værre end lineært betragtes som en dårlig kompleksitet (dvs. ineffektiv) og bør undgås, hvis det er muligt. Lineær kompleksitet er okay og normalt et nødvendigt onde. Logaritmisk er godt. Constant er fantastisk!

For at få en idé om, hvordan en Big-O beregnes, lad os tage et kig på nogle eksempler på konstant, lineær og kvadratisk kompleksitet.

Konstant kompleksitet - O(C)

Kompleksiteten af ​​en algoritme siges at være konstant, hvis de nødvendige trin for at fuldføre udførelsen af ​​en algoritme forbliver konstante, uanset antallet af input. Den konstante kompleksitet er betegnet med O (c) hvor c kan være et hvilket som helst konstant tal.

Lad os skrive en simpel algoritme i Python, der finder kvadratet af det første element på listen og derefter udskriver det på skærmen:

def constant_algo(items):
    result = items[0] * items[0]
    print(result)

constant_algo([4, 5, 6, 8])

I scriptet ovenfor, uanset inputstørrelsen, eller antallet af elementer på inputlisten items, udfører algoritmen kun 2 trin:

1. Find kvadratet af det første element
2. Udskriver resultatet på skærmen.

Derfor forbliver kompleksiteten konstant.

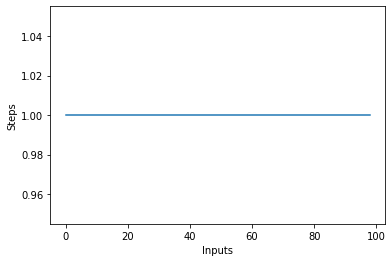
Hvis du tegner et linjeplot med den varierende størrelse af items input på X-aksen og antallet af trin på Y-aksen, får du en ret linje. Lad os lave et kort script, der hjælper os med at visualisere dette. Uanset antallet af input, forbliver antallet af udførte trin det samme:

steps = []
def constant(n):
    return 1
    
for i in range(1, 100):
    steps.append(constant(i))
plt.plot(steps)

Lineær kompleksitet – O (n)

Kompleksiteten af ​​en algoritme siges at være lineær, hvis de nødvendige trin for at fuldføre udførelsen af ​​en algoritme stiger eller falder lineært med antallet af input. Lineær kompleksitet er betegnet med O (n).

Lad os i dette eksempel skrive et simpelt program, der viser alle elementer på listen til konsollen:

def linear_algo(items):
    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Kompleksiteten af linear_algo() funktion er lineær i ovenstående eksempel, da antallet af iterationer af for-løkken vil være lig med størrelsen af ​​input items matrix. For eksempel, hvis der er 4 genstande i items liste, vil for-løkken blive udført 4 gange.

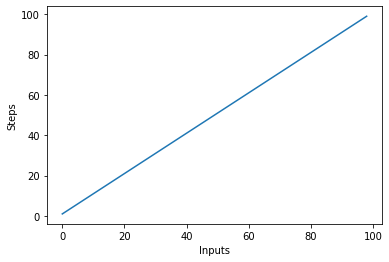
Lad os hurtigt lave et plot for den lineære kompleksitetsalgoritme med antallet af input på x-aksen og antallet af trin på y-aksen:

steps = []
def linear(n):
    return n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

Dette vil resultere i:

En vigtig ting at bemærke er, at med store input har konstanter tendens til at miste værdi. Det er derfor, vi typisk fjerner konstanter fra Big-O notation, og et udtryk som O(2n) forkortes normalt til O(n). Både O(2n) og O(n) er lineære - det lineære forhold er det afgørende, ikke den konkrete værdi. Lad os for eksempel ændre linear_algo():

def linear_algo(items):
    for item in items:
        print(item)

    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Der er to for-loops, der itererer over inputtet items liste. Derfor bliver kompleksiteten af ​​algoritmen O (2n), men i tilfælde af uendelige elementer i inputlisten, er to gange uendeligt stadig lig med uendelig. Vi kan ignorere konstanten 2 (da den i sidste ende er ubetydelig) og kompleksiteten af ​​algoritmen forbliver O (n).

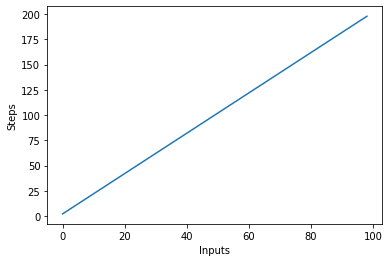
Lad os visualisere denne nye algoritme ved at plotte inputs på X-aksen og antallet af trin på Y-aksen:

steps = []
def linear(n):
    return 2*n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

I scriptet ovenfor kan du tydeligt se det y=2noutputtet er dog lineært og ser sådan ud:

Kvadratisk kompleksitet – O(n²)

Kompleksiteten af ​​en algoritme siges at være kvadratisk, når de nødvendige trin for at udføre en algoritme er en kvadratisk funktion af antallet af elementer i inputtet. Kvadratisk kompleksitet betegnes som O(n²):

def quadratic_algo(items):
    for item in items:
        for item2 in items:
            print(item, ' ' ,item2)

quadratic_algo([4, 5, 6, 8])

Vi har en ydre sløjfe, der itererer gennem alle elementerne i inputlisten og derefter en indlejret indre loop, som igen itererer gennem alle elementerne i inputlisten. Det samlede antal udførte trin er n*n, hvor n er antallet af elementer i input-arrayet.

Følgende graf plotter antallet af input mod trinene for en algoritme med kvadratisk kompleksitet:

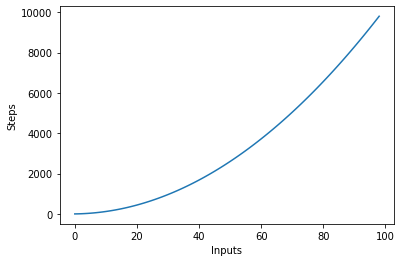
Logaritmisk kompleksitet – O (logn)

Nogle algoritmer opnår logaritmisk kompleksitet, som f.eks Binær søgning. Binær søgning søger efter et element i et array ved at markere Midt af et array og beskæring af den halvdel, hvori elementet ikke er. Det gør det igen for den resterende halvdel og fortsætter de samme trin, indtil elementet er fundet. I hvert trin er det halvdele antallet af elementer i arrayet.

Dette kræver, at arrayet er sorteret, og at vi laver en antagelse om dataene (såsom at de er sorteret).

Når du kan lave antagelser om de indgående data, kan du tage skridt, der reducerer kompleksiteten af ​​en algoritme. Logaritmisk kompleksitet er ønskelig, da den opnår god ydeevne selv med højt skaleret input.

Finder du kompleksiteten af ​​komplekse funktioner?

I tidligere eksempler havde vi ret simple funktioner på input. Men hvordan beregner vi Big-O af funktioner, der kalder (flere) andre funktioner på inputtet?

Lad os tage et kig:

def complex_algo(items):

    for i in range(5):
        print("Python is awesome")

    for item in items:
        print(item)

    for item in items:
        print(item)

    print("Big O")
    print("Big O")
    print("Big O")

complex_algo([4, 5, 6, 8])

I scriptet ovenfor udføres flere opgaver, først udskrives en streng 5 gange på konsollen ved hjælp af print udmelding. Dernæst udskriver vi inputlisten to gange på skærmen, og til sidst udskrives endnu en streng tre gange på konsollen. For at finde kompleksiteten af ​​en sådan algoritme skal vi nedbryde algoritmekoden i dele og forsøge at finde kompleksiteten af ​​de enkelte stykker. Marker kompleksiteten af ​​hvert stykke.

I det første afsnit har vi:

for i in range(5):
	print("Python is awesome")

Kompleksiteten af ​​denne del er O (5) da fem konstante trin udføres i dette stykke kode uanset input.

Dernæst har vi:

for item in items:
	print(item)

Vi ved, at kompleksiteten af ​​ovenstående kodestykke er O (n). På samme måde er kompleksiteten af ​​det følgende stykke kode også O (n):

for item in items:
	print(item)

Til sidst, i det følgende stykke kode, udskrives en streng tre gange, derfor er kompleksiteten O (3):

print("Big O")
print("Big O")
print("Big O")

For at finde den overordnede kompleksitet skal vi blot tilføje disse individuelle kompleksiteter:

O(5) + O(n) + O(n) + O(3)

For at forenkle ovenstående får vi:

O(8) + O(2n) = O(8+2n)

Vi sagde tidligere, at når inputtet (som har længden n i dette tilfælde) bliver ekstremt stort, bliver konstanterne ubetydelige, dvs. to gange eller halvdelen af ​​uendeligheden forbliver stadig uendelig. Derfor kan vi ignorere konstanterne. Den endelige kompleksitet af algoritmen vil være O (n)!

Worst vs Best Case Complexity

Normalt, når nogen spørger dig om kompleksiteten af ​​en algoritme - er de interesserede i den værste tilfælde kompleksitet (Big-O). Nogle gange kan de også være interesserede i den bedste kompleksitet (Big-Omega).

For at forstå forholdet mellem disse, lad os tage et kig på et andet stykke kode:

def search_algo(num, items):
    for item in items:
        if item == num:
            return True
        else:
            pass
nums = [2, 4, 6, 8, 10]

print(search_algo(2, nums))

I scriptet ovenfor har vi en funktion, der tager et tal og en liste over tal som input. Det returnerer sandt, hvis det beståede tal findes på listen over tal, ellers vender det tilbage None. Søger du på 2 på listen, vil den blive fundet i den første sammenligning. Dette er den bedste kompleksitet af algoritmen, idet det søgte emne findes i det først søgte indeks. Den bedste sagskompleksitet, i dette tilfælde er O (1). På den anden side, hvis du søger 10, vil den blive fundet ved det sidst søgte indeks. Algoritmen skal derfor søge gennem alle elementerne på listen den værste kompleksitet bliver O (n).

Udover best og worst case kompleksitet, kan du også beregne den gennemsnitlige kompleksitet (Big-Theta) af en algoritme, som fortæller dig "ud fra et tilfældigt input, hvad er den forventede tidskompleksitet af algoritmen"?

Rumkompleksitet

Ud over tidskompleksiteten, hvor du tæller antallet af trin, der kræves for at fuldføre udførelsen af ​​en algoritme, kan du også finde rumkompleksitet som refererer til mængden af ​​plads, du skal allokere i hukommelsen under udførelsen af ​​et program.

Tag et kig på følgende eksempel:

def return_squares(n):
    square_list = []
    for num in n:
        square_list.append(num * num)

    return square_list

nums = [2, 4, 6, 8, 10]
print(return_squares(nums))

return_squares() funktion accepterer en liste over heltal og returnerer en liste med de tilsvarende kvadrater. Algoritmen skal allokere hukommelse til det samme antal elementer som i inputlisten. Derfor bliver rumkompleksiteten af ​​algoritmen O (n).

Konklusion

Big-O-notationen er standardmetrikken, der bruges til at måle kompleksiteten af ​​en algoritme. I denne guide har vi studeret, hvad Big-O-notation er, og hvordan det kan bruges til at måle kompleksiteten af ​​en række algoritmer. Vi studerede også forskellige typer af Big-O-funktioner ved hjælp af forskellige Python-eksempler. Til sidst gennemgik vi kort den værste og bedste sagskompleksitet sammen med rumkompleksiteten.