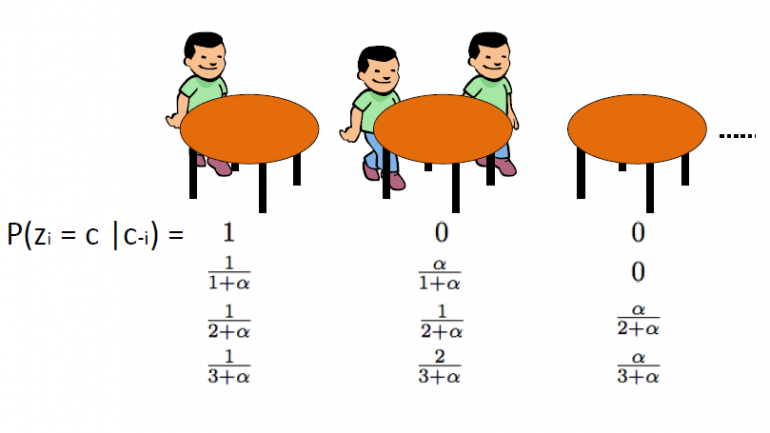Dirichlet-processen den kinesiske restaurantproces og andre repræsentationer

• Maj 20, 2014
• Vasilis Vryniotis
• . Ingen kommentarer

Denne artikel er tredje del af serien om Clustering med Dirichlet Process Mixture Models. Den forrige gang definerede vi Finite Mixture Model baseret på Dirichlet Distribution, og vi stillede spørgsmål om, hvordan vi kan gøre netop denne model uendelig. Vi diskuterede kort ideen om at tage grænsen for modellen, når k-antallet af klynger har en tendens til uendeligt, men som vi understregede, er eksistensen af ​​et sådant objekt ikke trivielt (med andre ord, hvordan tager vi egentlig grænsen for en model ”?). Som en påmindelse er grunden til, at vi ønsker at gøre k uendelig, fordi vi på denne måde vil have en ikke-parametrisk model, som ikke kræver, at vi foruddefinerer det samlede antal klynger i dataene.

Opdatering: Datumbox Machine Learning Framework er nu open source og gratis til downloade. Tjek pakken com.datumbox.framework.machinelearning.clustering for at se implementeringen af ​​Dirichlet Process Mixture Models i Java.

Selvom vores mål er at bygge en model, der er i stand til at udføre clustering på datasæt, skal vi inden da diskutere Dirichlet-processer. Vi vil give både de strenge matematiske definitioner og de mere intuitive forklaringer af DP, og vi vil diskutere måder at konstruere processen på. Disse konstruktioner/repræsentationer kan ses som en måde at finde forekomster af Dirichlet-processen i "det virkelige liv".

På trods af at jeg forsøgte at tilpasse min forskningsrapport på en sådan måde, at disse blogindlæg er nemmere at følge, er det stadig vigtigt at definere de nødvendige matematiske værktøjer og distributioner, inden vi springer i gang med at bruge modellerne. Dirichlet-procesmodeller er et emne for aktiv forskning, men de kræver at have en god forståelse af statistik og stokastiske processer, før de bruges. Et andet problem er, at som vi vil se i denne artikel, kan Dirichlet-processer repræsenteres/konstrueres på mange måder. Som følge heraf bruger flere akademiske artikler helt forskellige notation/konventioner og undersøger problemet fra forskellige synsvinkler. I dette indlæg forsøger jeg at forklare dem så enkelt som muligt og bruge den samme notation. Forhåbentlig bliver tingene klarere med de to kommende artikler, som fokuserer på definitionen af ​​Dirichlet Process Mixture Models og på, hvordan man rent faktisk bruger dem til at udføre klyngeanalyse.

1. Definition af Dirichlet Process

En Dirichlet-proces over et Θ-rum er en stokastisk proces. Det er en sandsynlighedsfordeling over "sandsynlighedsfordelinger over Θ rum" og en trække fra det er en diskret fordeling. Mere formelt er en Dirichlet-fordeling en fordeling over sandsynlighedsmål. EN sandsynlighedsmål er en funktion af delmængder af rummet Θ til [0,1]. G er et DP-fordelt tilfældigt sandsynlighedsmål, betegnet som , hvis for en partition (A₁,…EN_n) af plads Θ det har vi .

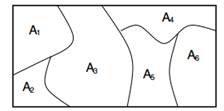
Figur 1: Marginaler på finite partitioner er Dirichlet-fordelt.

DP har to parametre: Den første er basisfordelingen G₀ der tjener som et middel . Den anden er styrkeparameteren α, som er strengt positiv og fungerer som omvendt varians . Det bestemmer omfanget af gentagelsen af ​​værdierne af outputfordelingen. Jo højere værdien af ​​a, jo mindre gentagelse; jo mindre værdien er, jo højere er gentagelsen af ​​værdierne for outputfordelingen. Endelig er Θ-rummet det parameterrum, hvorpå vi definerer DP. Rummet Θ er desuden også definitionsrummet for G₀ som er den samme som G.

En enklere og mere intuitiv måde at forklare en Dirichlet-proces er følgende. Antag, at vi har et mellemrum Θ, der kan opdeles på enhver endelig måde (A₁,…,EN_n) og en sandsynlighedsfordeling G, som tildeler sandsynligheder til dem. G er en specifik sandsynlighedsfordeling over Θ, men der er mange andre. Dirichlet-processen på Θ modellerer præcis dette; det er en fordeling over alle mulige sandsynlighedsfordelinger på rummet Θ. Dirichlet-processen er parametriseret med G₀ basefunktion og α-koncentrationsparameteren. Vi kan sige, at G er fordelt efter DP med parametrene α og G₀ hvis den fælles fordeling af de sandsynligheder, som G tildeler partitionerne af Θ, følger Dirichlet-fordelingen. Alternativt kan vi sige, at de sandsynligheder, som G tildeler enhver endelig partition af Θ, følger Dirichlet-fordelingen.

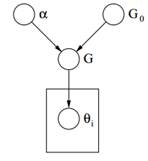
Figur 2: Grafisk model af Dirichlet-processen

Endelig ovenfor kan vi se grafisk model af en DP. Vi skal bemærke, at α er en skalær hyperparameter, G₀ er basisfordelingen af ​​DP, G en tilfældig fordeling over Θ parameterrum samplet fra DP, som tildeler sandsynligheder til parametrene og θ_i er en parametervektor, som er tegnet fra G-fordelingen, og den er et element af Θ-rum.

2. Posteriore Dirichlet-processer

De bageste Dirichlet-processer blev diskuteret af Ferguson. Vi starter med at tegne et tilfældigt sandsynlighedsmål G fra en Dirichlet-proces, . Da G er en sandsynlighedsfordeling over Θ, kan vi også prøve fra denne fordeling og trække uafhængige identisk fordelte prøver θ₁,…, θ_n ~ G. Da tegninger fra en Dirichlet-proces er diskrete fordelinger, kan vi repræsentere hvor er en kort notation for som er en deltafunktion, der tager 1 if og 0 andre steder. En interessant effekt af dette er, at da G er defineret på denne måde, er der en positiv sandsynlighed for, at forskellige prøver har samme værdi . Som vi vil se senere, skaber dette en klyngeeffekt, der kan bruges til at udføre Cluster Analysis på datasæt.

Ved at bruge ovenstående definitioner og observationer ønsker vi at estimere bagsiden af ​​Dirichlet-processen givet prøverne θ. Ikke desto mindre siden vi ved det , ved at bruge Bayes-reglerne og konjugationen mellem Dirichlet og Multinomial har vi det , .

Ligning 1: Posterior Dirichlet-proces

Denne ejendom er meget vigtig, og den bruges af de forskellige DP-repræsentationer.

3. Dirichlet Proces repræsentationer

I de foregående segmenter definerede vi Dirichlet-processen og præsenterede dens teoretiske model. Et vigtigt spørgsmål, som vi skal besvare, er, hvordan ved vi, at et sådant objekt eksisterer, og hvordan vi kan konstruere og repræsentere en Dirichlet-proces.

De første indikationer på eksistens blev leveret af Ferguson som brugte Kolmogorov-konsistenssætningen, gav definitionen af ​​en Dirichlet-proces og beskrev den bageste Dirichlet-proces. Fortsætter sin forskning, Blackwell og MacQueen brugte de Finetti's sætning til at bevise eksistensen af ​​et sådant tilfældigt sandsynlighedsmål og introducerede Blackwell-MacQueen urneskemaet, som tilfredsstiller egenskaberne ved Dirichlet Process. I 1994 Sethuraman gav en ekstra enkel og direkte måde at konstruere en DP ved at introducere den Stick-breaking konstruktion. Endelig blev der leveret endnu en repræsentation af Aldous der introducerede den kinesiske restaurantproces som en effektiv måde at konstruere en Dirichlet-proces på.

De forskellige repræsentationer af Dirichlet-processen er matematisk ækvivalente, men deres formulering er forskellig, fordi de undersøger problemet fra forskellige synsvinkler. Nedenfor præsenterer vi de mest almindelige repræsentationer, der findes i litteraturen, og vi fokuserer på den kinesiske restaurantproces, som giver en enkel og beregningseffektiv måde at konstruere inferensalgoritmer for Dirichlet-processen.

3.1 Blackwell-MacQueen urneordningen

Blackwell-MacQueen urneordningen kan bruges til at repræsentere en Dirichlet-proces, og den blev introduceret af Blackwell og MacQueen. Den er baseret på Pólya-urneordningen, der kan ses som den modsatte model for prøveudtagning uden udskiftning. I Pólya-urneskemaet antager vi, at vi har en ikke-gennemsigtig urne, der indeholder farvede kugler, og vi trækker kugler tilfældigt. Når vi tegner en kugle, observerer vi dens farve, vi sætter den tilbage i urnen, og vi tilføjer en ekstra kugle af samme farve. Et lignende skema bruges af Blackwell og MacQueen til at konstruere en Dirichlet-proces.

Dette skema producerer en sekvens af θ₁,θ₂,... med betingede sandsynligheder . I dette skema antager vi, at G₀ er en fordeling over farver og hver θ_n repræsenterer farven på kuglen, der er placeret i urnen. Det algoritme er som følger:

· Vi starter med en tom urne.

· Med sandsynlighed proportional med α vi tegner og vi tilføjer en kugle af denne farve i urnen.

· Med sandsynlighed proportional med n-1 trækker vi en tilfældig kugle fra urnen, vi observerer dens farve, vi placerer den tilbage til urnen og vi tilføjer en ekstra kugle af samme farve i urnen.

Tidligere startede vi med en Dirichlet-proces og udledte Blackwell-MacQueen-skemaet. Lad os nu starte omvendt fra Blackwell-MacQueen-skemaet og udlede DP. Siden θ_i blev trukket på en iid måde fra G, vil deres fælles fordeling være invariant i forhold til eventuelle endelige permutationer, og de er derfor udskiftelige. Ved at bruge de Finetti's sætning har vi derfor, at der skal eksistere en fordeling over mål for at gøre dem iid, og denne fordeling er Dirichlet-processen. Som et resultat beviser vi, at Blackwell-MacQueen urneskemaet er en repræsentation af DP, og det giver os en konkret måde at konstruere det på. Som vi vil se senere, svarer denne ordning matematisk til den kinesiske restaurantproces.

3.2 Den pindbrydende konstruktion

Stick-breaking-konstruktionen er en alternativ måde at repræsentere en Dirichlet-proces, som blev introduceret af Sethuraman. Det er en konstruktiv måde at danne distribution og bruger efter analogi: Vi antager, at vi har en pind med længden 1, vi brækker den i position β₁ og vi tildeler π₁ lig med længden af ​​den del af pinden, som vi knækkede. Vi gentager den samme proces for at opnå π₂, Pi₃,… etc; på grund af den måde, som denne ordning er defineret på, kan vi fortsætte med at gøre det uendeligt mange gange.

Baseret på ovenstående er π_k kan modelleres som , Hvor mens θ som i de foregående skemaer samples direkte af basisfordelingen . Følgelig kan G-fordelingen skrives som summen af ​​deltafunktioner vægtet med π_k sandsynligheder, som er lig med . Den Stick-breaking-konstruktion giver os således en enkel og intuitiv måde at konstruere en Dirichlet-proces på.

3.3 Den kinesiske restaurantproces

Den kinesiske restaurantproces, som blev introduceret af Aldous, er en anden effektiv måde at repræsentere en Dirichlet-proces, og den kan linkes direkte til Blackwell-MacQueen urne-skemaet. Denne ordning bruger efter analogi: Vi går ud fra, at der er en kinesisk restaurant med uendeligt mange borde. Når kunderne kommer ind i restauranten, sætter de sig tilfældigt ved et af de besatte borde, eller de vælger at sidde ved det første ledige tomme bord.

CRP definerer en fordeling på rummet af partitioner af de positive heltal. Vi starter med at tegne θ₁,…θ_n fra Blackwell-MacQueen urneordning. Som vi diskuterede i de foregående segmenter, forventer vi at se en klyngeeffekt, og dermed vil det samlede antal unikke θ-værdier k være væsentligt mindre end n. Dette definerer således en partition af mængden {1,2,…,n} i k klynger. Tegning fra Blackwell-MacQueen urneskemaet inducerer derfor en tilfældig partition af {1,2,...,n}-sættet. Den kinesiske restaurantproces er dette induceret fordeling over skillevægge. Algoritmen er som følger:

· Vi starter med en tom restaurant.

· Den 1^st kunde sidder altid på 1^st bord

· n+1^th kunden har 2 muligheder:

o Sæt dig på det 1. ledige bord med sandsynlighed

o Sid på et af de kth besatte borde med sandsynlighed
hvor er antallet af personer, der sidder på det bord

Hvor α er spredningsværdien af ​​DP og n er det samlede antal kunder i restauranten på et givet tidspunkt. Den latente variabel z_i gemmer tabelnummeret på i^th kunde og tager værdier fra 1 til k_n hvor k_n er det samlede antal besatte borde, når n kunder er i restauranten. Vi skal bemærke, at k_n vil altid være mindre eller lig med n og i gennemsnit er det ca . Endelig skal vi bemærke, at sandsynligheden for bordopstilling er invariant for permutationer. Således z_i er udskiftelig, hvilket indebærer, at tabeller med samme størrelse af kunder har samme sandsynlighed.

Den kinesiske restaurantproces er stærkt forbundet med Pólya-urneordningen og Dirichlet-processen. CRP er en måde at specificere en fordeling over skillevægge (tabeltildelinger) på n point og kan bruges som forud for rummet af latent variabel z_i som bestemmer klyngetildelingerne. CRP'en svarer til Pólyas urneskema med den eneste forskel, at den ikke tildeler parametre til hver tabel/klynge. At gå fra CRP til Pólyas urneordning vi tegner for alle tabeller k=1,2… og derefter for hver x_i som er grupperet til tabel z_i tildele en . Med andre ord tildele til det nye x_i parameteren θ i tabellen. Endelig siden vi kan ikke tildele θ til uendelige tabeller fra begyndelsen, kan vi bare tildele et nyt θ hver gang nogen sætter sig på et nyt bord. På grund af alt ovenstående kan CRP'et hjælpe os med at opbygge beregningseffektive algoritmer til at udføre Cluster Analysis på datasæt.

I dette indlæg diskuterede vi Dirichlet-processen og flere måder at konstruere den på. Vi vil bruge ovenstående ideer i den næste artikel. Vi vil introducere Dirichlet-procesblandingsmodellen, og vi vil bruge den kinesiske restaurantrepræsentation til at konstruere Dirichlet-processen og udføre klyngeanalyse. Hvis du gik glip af nogle få punkter, så fortvivl ikke, da tingene begynder at blive klarere med de næste to artikler.

Jeg håber du fandt dette indlæg interessant. Hvis du gjorde det, så brug et øjeblik på at dele det på Facebook og Twitter. 🙂