1ICFO-Institut de Ciencies Fotoniques, Barcelona Institute of Science and Technology, 08860 Castelldefels, Spanien
2CFIS-Centre de Formació Interdisciplinària Superior, UPC-Universitat Politècnica de Catalunya, 08028 Barcelona, Spanien
3Univ Grenoble Alpes, CNRS, Grenoble INP, Institut Néel, 38000 Grenoble, Frankrig
4ICREA-Institucio Catalana de Recerca i Estudis Avançats, Lluis Companys 23, 08010 Barcelona, Spanien
Finder du denne artikel interessant eller vil du diskutere? Scite eller efterlade en kommentar på SciRate.
Abstrakt
Gensidigt upartiske baser svarer til meget nyttige par af målinger i kvanteinformationsteori. I den mindste sammensatte dimension, seks, er det kendt, at der eksisterer mellem tre og syv gensidigt upartiske baser, med en årtier gammel formodning, kendt som Zauners formodning, der siger, at der højst eksisterer tre. Her tackler vi Zauners formodning numerisk gennem konstruktionen af Bell-uligheder for hvert par af heltal $n,d ge 2$, der maksimalt kan krænkes i dimension $d$, hvis og kun hvis $n$ MUB'er findes i den dimension. Derfor gør vi Zauners formodning til et optimeringsproblem, som vi løser ved hjælp af tre numeriske metoder: vippeoptimering, ikke-lineær semibestemt programmering og Monte Carlo-teknikker. Alle tre metoder identificerer korrekt de kendte tilfælde i lave dimensioner, og alle antyder, at der ikke eksisterer fire gensidigt upartiske baser i dimension seks, hvor alle finder de samme baser, der numerisk optimerer den tilsvarende Bell-ulighed. Desuden ser disse numeriske optimeringsmidler ud til at falde sammen med de "fire fjerneste baser" i dimension seks, fundet ved numerisk optimering af et afstandsmål i [P. Raynal, X. Lu, B.-G. Englert, {Phys. Rev. A}, { 83} 062303 (2011)]. Endelig tyder Monte Carlo-resultaterne på, at der højst eksisterer tre MUB'er i dimension ti.
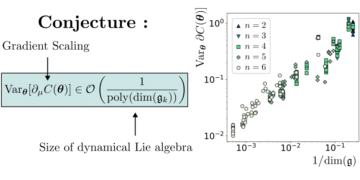
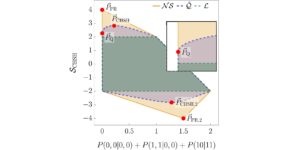
Udvalgt billede: Den relative forskel mellem værdien af vores Bell-uligheder, hvis det antages, at n MUB'er eksisterer i dimension d og værdien fundet ved vores numeriske metoder. Nulværdier betyder, at metoderne fandt n MUB'er i dimension d, mens ikke-nulværdier betyder, at metoderne ikke fandt n MUB'er i dimension d. Alle de kendte tilfælde (dimensioner to til fem og dimension seks med to og tre MUB'er) er korrekt identificeret med numerikken. I dimension seks finder ingen af metoderne fire MUB'er, og alle metoderne konvergerer til det samme sæt af fire baser.
Populært resumé
På trods af deres brede anvendelse er der stadig åbne spørgsmål vedrørende strukturen af MUB'er. Mest fremtrædende er det maksimale antal målinger, der er parvist objektive ("antallet af MUB'er") ukendt, hvis dimensionen af kvantesystemet er et sammensat tal. Især i dimension seks ved vi kun, at antallet af MUB'er er mellem tre og syv. En langvarig åben formodning er Zauners, der siger, at der ikke eksisterer mere end tre MUB'er i dimension seks. Denne årtier lange formodning understøttes af nogle numeriske beviser, men der findes ingen beviser den dag i dag.
I dette arbejde tackler vi Zauners formodning gennem Bell ikke-lokalitet. Bell non-locality vedrører to forsøgspersoner, som ikke må kommunikere, men som kan dele nogle sammenhænge i form af klassisk tilfældighed eller en delt kvantetilstand. Det har vist sig, at deling af kvanteressourcer kan føre til eksperimentelle data, der ikke kan forklares med klassisk fysik (mere præcist ved såkaldte lokale skjulte variable modeller). Dette er kendt som Bells teorem, og det er blevet eksperimentelt verificeret i det sidste årti. At vidne til ikke-klassiciteten af eksperimentelle data sker oftest via såkaldte Bell-uligheder, som er funktioner af de målingsudfaldssandsynligheder, der forekommer i eksperimentet. Klassiske data skal tilfredsstille Bell-uligheder, mens kvantedata kan krænke dem.
For nylig er der fundet Bell-uligheder, der maksimalt bliver overtrådt, hvis en af parterne anvender et par MUB-målinger af en given dimension. I dette arbejde udvider vi disse uligheder til nye, maksimalt krænket af et udvalgt antal MUB-målinger i en given dimension. Desuden, hvis dimensionen i eksperimentet er fast, opnås den maksimale overtrædelse, hvis og kun hvis de anvendte målinger svarer til det valgte antal MUB'er i den givne dimension. Derfor er beslutningen om, hvorvidt et udvalgt antal MUB'er eksisterer i en given dimension, ækvivalent med at finde den maksimale krænkelse af den tilsvarende Bell-ulighed i denne faste dimension.
Selvom det generelt er et svært problem at finde denne maksimale overtrædelse, bruger vi tre forskellige numeriske metoder som et forsøg på at finde den maksimale krænkelse af vores Bell-uligheder i en fast dimension. To af disse metoder er varianter af semidefinite programmeringsteknikker, mens den tredje er inspireret af statistisk fysik og kaldes simuleret annealing. Mens alle disse metoder er heuristiske - det vil sige, der er ingen garanti for, at de vil finde problemets sande optimum - kan man måle deres ydeevne ved at anvende dem på optimeringsproblemer, hvis optimum er kendt. Især finder vi, at alle de tre metoder er korrekt i stand til at identificere MUB-målinger i de tilfælde, hvor de vides at eksistere. Desuden, i de tilfælde, hvor de vides ikke at eksistere, konvergerer alle tre metoder til det samme sæt af målinger op til numerisk præcision. Vi anvender derefter vores metoder på det første ukendte tilfælde, det vil sige fire MUB'er i dimension seks. Ingen af metoderne er i stand til at identificere fire MUB'er i dimension seks, men igen konvergerer de alle til det samme sæt af fire målinger op til numerisk præcision. Ydermere finder den simulerede udglødningsteknik ikke fire MUB'er i den næste sammensatte dimension, dimension ti. Derfor, mens strenge påstande ikke kan fremsættes på grund af vores teknikkers heuristiske natur, understøtter vores resultater Zauners formodning fra det nye perspektiv om Bells ikke-lokalitet.
► BibTeX-data
► Referencer
[1] ID Ivanovic. Geometrisk beskrivelse af kvanttilstandsbestemmelse. Journal of Physics A: Mathematical and General, 14(12):3241–3245, 1981. doi:10.1088/0305-4470/14/12/019.
https://doi.org/10.1088/0305-4470/14/12/019
[2] G. Brassard CH Bennett. Kvantekryptografi: Offentlig nøgledistribution og møntkastning. Proceedings of IEEE International Conference on Computers, Systems and Signal Processing (IEEE, 1984), 175:8, 1984. doi:10.1016/j.tcs.2011.08.039.
https:///doi.org/10.1016/j.tcs.2011.08.039
[3] Artur K. Ekert. Kvantekryptografi baseret på Bells teorem. Phys. Rev. Lett., 67:661–663, 1991. doi:10.1103/PhysRevLett.67.661.
https:///doi.org/10.1103/PhysRevLett.67.661
[4] Dagmar Bruß. Optimal aflytning i kvantekryptografi med seks tilstande. Phys. Rev. Lett., 81:3018–3021, 1998. doi:10.1103/PhysRevLett.81.3018.
https:///doi.org/10.1103/PhysRevLett.81.3018
[5] Armin Tavakoli, Alley Hameedi, Breno Marques og Mohamed Bourennane. Quantum random access-koder ved hjælp af enkelt $d$-niveau systemer. Phys. Rev. Lett., 114:170502, 2015. doi:10.1103/PhysRevLett.114.170502.
https:///doi.org/10.1103/PhysRevLett.114.170502
[6] Máté Farkas og Jędrzej Kaniewski. Selvtest af gensidigt objektive baser i forberedelse-og-mål-scenariet. Phys. Rev. A, 99:032316, 2019. doi:10.1103/PhysRevA.99.032316.
https:///doi.org/10.1103/PhysRevA.99.032316
[7] H. Bechmann-Pasquinucci og N. Gisin. Klokkeulighed for qunits med binære målinger. Kvante info. Comput., 3(2):157–164, 2003. doi:10.26421/QIC3.2-6.
https:///doi.org/10.26421/QIC3.2-6
[8] Jędrzej Kaniewski, Ivan Šupić, Jordi Tura, Flavio Baccari, Alexia Salavrakos og Remigiusz Augusiak. Maksimal ikke-lokalitet fra maksimal sammenfiltring og gensidigt upartiske baser og selvtest af to-qutrit kvantesystemer. Quantum, 3:198, 2019. doi:10.22331/q-2019-10-24-198.
https://doi.org/10.22331/q-2019-10-24-198
[9] Armin Tavakoli, Máté Farkas, Denis Rosset, Jean-Daniel Bancal og Jędrzej Kaniewski. Gensidigt uvildige baser og symmetriske informationsmæssigt komplette målinger i Bell-eksperimenter. Science Advances, 7(7):eabc3847, 2021. doi:10.1126/sciadv.abc3847.
https:///doi.org/10.1126/sciadv.abc3847
[10] Thomas Durt, Berthold-Georg Englert, Ingemar Bengtsson og Karol Życzkowski. På gensidigt upartiske grundlag. International Journal of Quantum Information, 08(04):535–640, 2010. doi:10.1142/S0219749910006502.
https:///doi.org/10.1142/S0219749910006502
[11] William K Wootters og Brian D Fields. Optimal tilstandsbestemmelse ved gensidigt objektive målinger. Annals of Physics, 191(2):363–381, 1989. doi:10.1016/0003-4916(89)90322-9.
https://doi.org/10.1016/0003-4916(89)90322-9
[12] Paweł Wocjan og Thomas Beth. Nykonstruktion af gensidigt uvildige baser i kvadratiske dimensioner. Kvante info. Comput., 5(2):93–101, 2005. doi:10.26421/QIC5.2-1.
https:///doi.org/10.26421/QIC5.2-1
[13] Mihály Weiner. Et hul for det maksimale antal gensidigt upartiske baser. Proc. Amer. Matematik. Soc., 141:1963–1969, 2013. doi:10.1090/S0002-9939-2013-11487-5.
https://doi.org/10.1090/S0002-9939-2013-11487-5
[14] Gerhard Zauner. Quantendesigns: Grundzüge einer nichtkommutativen Designtheorie. Ph.d.-afhandling, 1999.
[15] P. Oscar Boykin, Meera Sitharam, Pham Huu Tiep og Pawel Wocjan. Gensidigt uvildige baser og ortogonale nedbrydninger af Lie-algebraer. Kvante info. Comput., 7(4):371–382, 2007. doi:10.26421/QIC7.4-6.
https:///doi.org/10.26421/QIC7.4-6
[16] Stephen Brierley og Stefan Weigert. Konstruktion af gensidigt uvildige baser i dimension seks. Phys. Rev. A, 79:052316, 2009. doi:10.1103/PhysRevA.79.052316.
https:///doi.org/10.1103/PhysRevA.79.052316
[17] Philippe Jaming, Máté Matolcsi, Péter Móra, Ferenc Szöllősi og Mihály Weiner. Et generaliseret Pauli-problem og en uendelig familie af MUB-tripletter i dimension 6. Journal of Physics A: Mathematical and Theoretical, 42(24):245305, maj 2009. doi:10.1088/1751-8113/42/24/ 245305.
https://doi.org/10.1088/1751-8113/42/24/245305
[18] Gary McConnell, Harry Spencer og Afaq Tahir. Beviser for og imod Zauners MUB-formodning i $mathbb{C}^6$. 2021. doi:10.48550/arXiv.2103.08703.
https:///doi.org/10.48550/arXiv.2103.08703
[19] Sander Gribling og Sven Polak. Gensidigt upartiske baser: polynomiel optimering og symmetri. 2021. doi:10.48550/arXiv.2111.05698.
https:///doi.org/10.48550/arXiv.2111.05698
[20] Ingemar Bengtsson, Wojciech Bruzda, Åsa Ericsson, Jan-Åke Larsson, Wojciech Tadej og Karol Życzkowski. Gensidigt upartiske baser og Hadamard-matricer af størrelsesorden seks. Journal of Mathematical Physics, 48(5):052106, 2007. doi:10.1063/1.2716990.
https:///doi.org/10.1063/1.2716990
[21] Philippe Raynal, Xin Lü og Berthold-Georg Englert. Gensidigt upartiske baser i seks dimensioner: De fire mest fjerne baser. Phys. Rev. A, 83:062303, 2011. doi:10.1103/PhysRevA.83.062303.
https:///doi.org/10.1103/PhysRevA.83.062303
[22] Edgar A. Aguilar, Jakub J. Borkała, Piotr Mironowicz og Marcin Pawłowski. Forbindelser mellem gensidigt upartiske baser og kvante tilfældige adgangskoder. Phys. Rev. Lett., 121:050501, 2018. doi:10.1103/PhysRevLett.121.050501.
https:///doi.org/10.1103/PhysRevLett.121.050501
[23] Nicolas Brunner, Daniel Cavalcanti, Stefano Pironio, Valerio Scarani og Stephanie Wehner. Bell ikke-lokalitet. Rev. Mod. Phys., 86:419–478, 2014. doi:10.1103/RevModPhys.86.419.
https:///doi.org/10.1103/RevModPhys.86.419
[24] MOSEK ApS. MOSEK Fusion API til C++ 9.2.49, 2021. URL: https:///docs.mosek.com/9.2/cxxfusion/index.html.
https:///docs.mosek.com/9.2/cxxfusion/index.html
[25] Hiroshi Yamashita, Hiroshi Yabe og Kouhei Harada. En primal-dual interior point-metode til ikke-lineær semidefinite programmering. Matematisk programmering, 135(1):89–121, 2012. doi:10.1007/s10107-011-0449-z.
https:///doi.org/10.1007/s10107-011-0449-z
[26] Stephen Boyd og Lieven Vandenberghe. Konveks optimering. Cambridge University Press, 2004. doi:10.1017/CBO9780511804441.
https:///doi.org/10.1017/CBO9780511804441
[27] S. Kirkpatrick, CD Gelatt og MP Vecchi. Optimering ved simuleret udglødning. Science, 220(4598):671–680, 1983. doi:10.1126/science.220.4598.671.
https://doi.org/10.1126/science.220.4598.671
[28] Nicholas Metropolis, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller og Edward Teller. Ligning af tilstandsberegninger med hurtige computere. The Journal of Chemical Physics, 21(6):1087–1092, 1953. doi:10.1063/1.1699114.
https:///doi.org/10.1063/1.1699114
[29] Miguel Navascués, Stefano Pironio og Antonio Acín. Afgrænsning af mængden af kvantekorrelationer. Phys. Rev. Lett., 98:010401, 2007. doi:10.1103/PhysRevLett.98.010401.
https:///doi.org/10.1103/PhysRevLett.98.010401
Citeret af
Dette papir er udgivet i Quantum under Creative Commons Attribution 4.0 International (CC BY 4.0) licens. Ophavsretten forbliver hos de originale copyright-indehavere, såsom forfatterne eller deres institutioner.