Big O-Notation und Algorithmusanalyse mit Python-Beispielen

Einleitung

Es gibt normalerweise mehrere Möglichkeiten, das Problem mit einem Computerprogramm zu lösen. Zum Beispiel gibt es mehrere Möglichkeiten, Elemente in einem Array zu sortieren – Sie können verwenden Zusammenführen, sortieren, Blase sortieren, Sortieren durch Einfügen, usw. Alle diese Algorithmen haben ihre eigenen Vor- und Nachteile, und die Aufgabe des Entwicklers besteht darin, sie abzuwägen, um den besten Algorithmus für jeden Anwendungsfall auswählen zu können. Mit anderen Worten, die Hauptfrage ist, welcher Algorithmus verwendet werden soll, um ein bestimmtes Problem zu lösen, wenn es mehrere Lösungen für das Problem gibt.

Algorithmusanalyse bezieht sich auf die Analyse der Komplexität verschiedener Algorithmen und das Finden des effizientesten Algorithmus zur Lösung des vorliegenden Problems. Big-O-Notation ist ein statistisches Maß zur Beschreibung der Komplexität des Algorithmus.

In diesem Leitfaden werfen wir zunächst einen kurzen Überblick über die Algorithmusanalyse und werfen dann einen tieferen Blick auf die Big-O-Notation. Wir werden sehen, wie die Big-O-Notation verwendet werden kann, um die Komplexität von Algorithmen mit Hilfe verschiedener Python-Funktionen zu finden.

Warum ist die Algorithmenanalyse wichtig?

Um zu verstehen, warum die Algorithmusanalyse wichtig ist, nehmen wir die Hilfe eines einfachen Beispiels. Angenommen, ein Manager gibt zwei seiner Mitarbeiter die Aufgabe, einen Algorithmus in Python zu entwerfen, der die Fakultät einer vom Benutzer eingegebenen Zahl berechnet. Der vom ersten Mitarbeiter entwickelte Algorithmus sieht so aus:

def fact(n):
    product = 1
    for i in range(n):
        product = product * (i+1)
    return product

print(fact(5))

Beachten Sie, dass der Algorithmus einfach eine ganze Zahl als Argument akzeptiert. Im Inneren des fact() Funktion eine Variable namens product wird initialisiert auf 1. Eine Schleife wird ausgeführt von 1 zu n und während jeder Iteration der Wert in der product wird mit der Zahl multipliziert, die von der Schleife durchlaufen wird, und das Ergebnis wird in gespeichert product wieder variabel. Nachdem die Schleife ausgeführt wurde, wird die product Variable enthält die Fakultät.

Ähnlich hat auch der zweite Mitarbeiter einen Algorithmus entwickelt, der die Fakultät einer Zahl berechnet. Der zweite Mitarbeiter verwendete eine rekursive Funktion, um die Fakultät der Zahl zu berechnen n:

def fact2(n):
    if n == 0:
        return 1
    else:
        return n * fact2(n-1)

print(fact2(5))

Der Manager muss entscheiden, welcher Algorithmus verwendet wird. Dazu haben sie entschieden, welcher Algorithmus schneller läuft. Eine Möglichkeit, dies zu tun, besteht darin, die Zeit zu finden, die erforderlich ist, um den Code für dieselbe Eingabe auszuführen.

Im Jupyter-Notebook können Sie die %timeit Literal, gefolgt vom Funktionsaufruf, um die Zeit zu ermitteln, die die Funktion zur Ausführung benötigt:

%timeit fact(50)

Dies wird uns geben:

9 µs ± 405 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Die Ausgabe sagt, dass der Algorithmus dauert 9 µs (plus/minus 45 Nanosekunden) pro Schleife.

In ähnlicher Weise können wir berechnen, wie viel Zeit die Ausführung des zweiten Ansatzes benötigt:

%timeit fact2(50)

Dies führt zu:

15.7 µs ± 427 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Der zweite Algorithmus mit Rekursion dauert 15 µs (plus/minus 427 Nanosekunden).

Die Ausführungszeit zeigt, dass der erste Algorithmus im Vergleich zum zweiten Algorithmus mit Rekursion schneller ist. Beim Umgang mit großen Eingaben kann der Leistungsunterschied signifikanter werden.

Die Ausführungszeit ist jedoch keine gute Metrik, um die Komplexität eines Algorithmus zu messen, da sie von der Hardware abhängt. Es wird eine objektivere Komplexitätsanalysemetrik für einen Algorithmus benötigt. Hier ist die Big O-Notation kommt zum spielen.

Algorithmusanalyse mit Big-O-Notation

Die Big-O-Notation bezeichnet die Beziehung zwischen der Eingabe in den Algorithmus und den zur Ausführung des Algorithmus erforderlichen Schritten. Es wird durch ein großes „O“ gefolgt von einer öffnenden und schließenden Klammer gekennzeichnet. Innerhalb der Klammern wird die Beziehung zwischen der Eingabe und den vom Algorithmus ausgeführten Schritten mit „n“ dargestellt.

Das Wichtigste zum Mitnehmen ist – Big-O interessiert sich nicht für a besondere Instanz, in der Sie einen Algorithmus ausführen, z fact(50), sondern eher, wie gut es tut Treppe bei steigendem Input. Dies ist eine viel bessere Metrik für die Bewertung als die konkrete Zeit für eine konkrete Instanz!

Wenn es zum Beispiel eine gibt lineare Beziehung zwischen der Eingabe und dem Schritt, den der Algorithmus unternimmt, um seine Ausführung abzuschließen, wird die verwendete Big-O-Notation sein O (n). Ebenso die Big-O-Notation für quadratische Funktionen is O(n²).

So bauen Sie Intuition auf:

• O (n): bei n=1, 1 Schritt wird ausgeführt. Bei n=10, werden 10 Schritte gemacht.
• O(n²): bei n=1, 1 Schritt wird ausgeführt. Bei n=10, werden 100 Schritte gemacht.

At n=1, diese beiden würden das Gleiche tun! Dies ist ein weiterer Grund, warum es besser ist, die Beziehung zwischen der Eingabe und der Anzahl der Schritte zur Verarbeitung dieser Eingabe zu beobachten, als nur Funktionen mit einigen konkreten Eingaben zu bewerten.

Im Folgenden sind einige der häufigsten Big-O-Funktionen aufgeführt:

Name und Vorname	Big O
Konstant	O (c)
Linear	O (n)
Quadratisch	O(n²)
Cubic	O(n³)
Exponentiell	O(2ⁿ)
Logarithmisch	O (log (n))
Linear protokollieren	O(nlog(n))

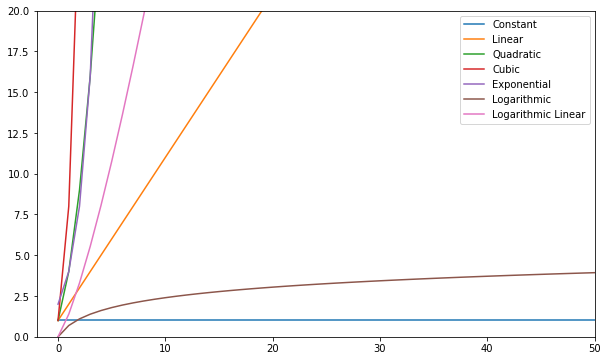
Sie können diese Funktionen visualisieren und vergleichen:

Allgemein gesagt gilt alles, was schlechter als linear ist, als schlechte Komplexität (dh ineffizient) und sollte nach Möglichkeit vermieden werden. Lineare Komplexität ist in Ordnung und meist ein notwendiges Übel. Logarithmisch ist gut. Konstant ist erstaunlich!

Um eine Vorstellung davon zu bekommen, wie ein Big-O berechnet wird, werfen wir einen Blick auf einige Beispiele konstanter, linearer und quadratischer Komplexität.

Konstante Komplexität – O (C)

Die Komplexität eines Algorithmus wird als konstant bezeichnet, wenn die zur Ausführung eines Algorithmus erforderlichen Schritte unabhängig von der Anzahl der Eingaben konstant bleiben. Die konstante Komplexität wird mit bezeichnet O (c) woher c kann eine beliebige konstante Zahl sein.

Lassen Sie uns einen einfachen Algorithmus in Python schreiben, der das Quadrat des ersten Elements in der Liste findet und es dann auf dem Bildschirm ausgibt:

def constant_algo(items):
    result = items[0] * items[0]
    print(result)

constant_algo([4, 5, 6, 8])

Im obigen Skript Unabhängig von der Eingabegröße, oder die Anzahl der Elemente in der Eingabeliste items, führt der Algorithmus nur 2 Schritte aus:

1. Finde das Quadrat des ersten Elements
2. Drucken des Ergebnisses auf dem Bildschirm.

Die Komplexität bleibt also konstant.

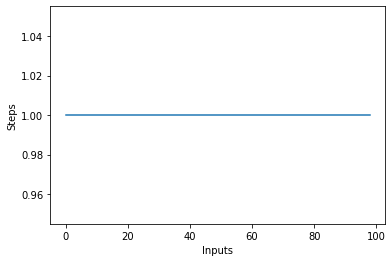
Wenn Sie ein Liniendiagramm mit unterschiedlicher Größe zeichnen items Eingabe auf der X-Achse und die Anzahl der Schritte auf der Y-Achse erhalten Sie eine gerade Linie. Lassen Sie uns ein kurzes Skript erstellen, um uns dies zu veranschaulichen. Unabhängig von der Anzahl der Eingaben bleibt die Anzahl der ausgeführten Schritte gleich:

steps = []
def constant(n):
    return 1
    
for i in range(1, 100):
    steps.append(constant(i))
plt.plot(steps)

Lineare Komplexität – O (n)

Die Komplexität eines Algorithmus wird als linear bezeichnet, wenn die zur Ausführung eines Algorithmus erforderlichen Schritte linear mit der Anzahl der Eingaben zunehmen oder abnehmen. Lineare Komplexität wird mit bezeichnet O (n).

Lassen Sie uns in diesem Beispiel ein einfaches Programm schreiben, das alle Elemente in der Liste auf der Konsole anzeigt:

def linear_algo(items):
    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Die Komplexität der linear_algo() Funktion ist im obigen Beispiel linear, da die Anzahl der Iterationen der for-Schleife sein wird gleich der Größe der Eingabe items Array. Wenn zum Beispiel 4 Artikel in der items list, wird die for-Schleife 4 Mal ausgeführt.

Lassen Sie uns schnell ein Diagramm für den linearen Komplexitätsalgorithmus mit der Anzahl der Eingaben auf der x-Achse und der Anzahl der Schritte auf der y-Achse erstellen:

steps = []
def linear(n):
    return n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

Dies führt zu:

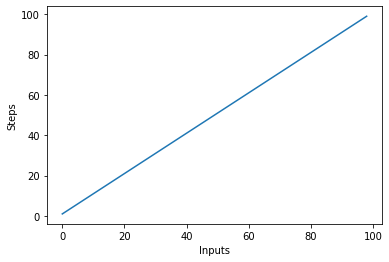
Es ist wichtig zu beachten, dass Konstanten bei großen Eingaben tendenziell an Wert verlieren. Aus diesem Grund entfernen wir normalerweise Konstanten aus der Big-O-Notation, und ein Ausdruck wie O(2n) wird normalerweise zu O(n) abgekürzt. Sowohl O(2n) als auch O(n) sind linear – die lineare Beziehung ist entscheidend, nicht der konkrete Wert. Ändern wir zum Beispiel die linear_algo():

def linear_algo(items):
    for item in items:
        print(item)

    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Es gibt zwei for-Schleifen, die über die Eingabe iterieren items aufführen. Daher wird die Komplexität des Algorithmus O (2n), aber im Fall von unendlichen Elementen in der Eingabeliste ist das Doppelte von Unendlich immer noch gleich Unendlich. Wir können die Konstante ignorieren 2 (da letztlich unbedeutend) und die Komplexität des Algorithmus bleibt O (n).

Lassen Sie uns diesen neuen Algorithmus visualisieren, indem wir die Eingaben auf der X-Achse und die Anzahl der Schritte auf der Y-Achse darstellen:

steps = []
def linear(n):
    return 2*n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

Im obigen Skript können Sie das deutlich sehen y=2n, die Ausgabe ist jedoch linear und sieht so aus:

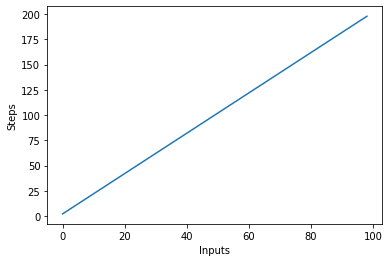
Quadratische Komplexität – O(n²)

Die Komplexität eines Algorithmus wird als quadratisch bezeichnet, wenn die zur Ausführung eines Algorithmus erforderlichen Schritte eine quadratische Funktion der Anzahl der Elemente in der Eingabe sind. Quadratische Komplexität wird als bezeichnet O(n²):

def quadratic_algo(items):
    for item in items:
        for item2 in items:
            print(item, ' ' ,item2)

quadratic_algo([4, 5, 6, 8])

Wir haben eine äußere Schleife, die alle Elemente in der Eingabeliste durchläuft, und dann eine verschachtelte innere Schleife, die wiederum alle Elemente in der Eingabeliste durchläuft. Die Gesamtzahl der durchgeführten Schritte ist n*n, wobei n die Anzahl der Elemente im Eingabearray ist.

Die folgende Grafik zeigt die Anzahl der Eingaben gegen die Schritte für einen Algorithmus mit quadratischer Komplexität:

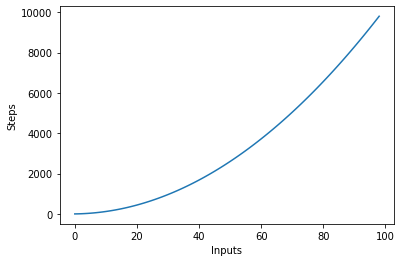
Logarithmische Komplexität – O (logn)

Einige Algorithmen erreichen eine logarithmische Komplexität, wie z Binäre Suche. Die binäre Suche sucht nach einem Element in einem Array, indem sie das überprüft mittel eines Arrays und Beschneiden der Hälfte, in der sich das Element nicht befindet. Er wiederholt dies für die verbleibende Hälfte und fährt mit den gleichen Schritten fort, bis das Element gefunden ist. In jedem Schritt, es Hälften die Anzahl der Elemente im Array.

Dazu muss das Array sortiert sein und wir müssen eine Annahme über die Daten treffen (z. B. dass sie sortiert sind).

Wenn Sie Annahmen über die eingehenden Daten treffen können, können Sie Maßnahmen ergreifen, die die Komplexität eines Algorithmus reduzieren. Logarithmische Komplexität ist wünschenswert, da sie auch bei stark skalierter Eingabe eine gute Performance erzielt.

Finden Sie die Komplexität komplexer Funktionen?

In den vorherigen Beispielen hatten wir ziemlich einfache Funktionen für die Eingabe. Aber wie berechnen wir das Big-O von Funktionen, die (mehrere) andere Funktionen für die Eingabe aufrufen?

Lass uns einen Blick darauf werfen:

def complex_algo(items):

    for i in range(5):
        print("Python is awesome")

    for item in items:
        print(item)

    for item in items:
        print(item)

    print("Big O")
    print("Big O")
    print("Big O")

complex_algo([4, 5, 6, 8])

Im obigen Skript werden mehrere Aufgaben ausgeführt, zuerst wird ein String 5 Mal auf der Konsole mit dem ausgegeben print Aussage. Als nächstes drucken wir die Eingabeliste zweimal auf dem Bildschirm, und schließlich wird eine weitere Zeichenfolge dreimal auf der Konsole gedruckt. Um die Komplexität eines solchen Algorithmus zu finden, müssen wir den Algorithmuscode in Teile zerlegen und versuchen, die Komplexität der einzelnen Teile zu finden. Notieren Sie die Komplexität jedes Stücks.

Im ersten Abschnitt haben wir:

for i in range(5):
	print("Python is awesome")

Die Komplexität dieses Teils ist O (5) da in diesem Codestück unabhängig von der Eingabe fünf konstante Schritte ausgeführt werden.

Als nächstes haben wir:

for item in items:
	print(item)

Wir wissen, wie komplex der obige Codeabschnitt ist O (n). Ähnlich ist auch die Komplexität des folgenden Codestücks O (n):

for item in items:
	print(item)

Schließlich wird im folgenden Codeabschnitt eine Zeichenfolge dreimal gedruckt, daher die Komplexität O (3):

print("Big O")
print("Big O")
print("Big O")

Um die Gesamtkomplexität zu finden, müssen wir einfach diese einzelnen Komplexitäten addieren:

O(5) + O(n) + O(n) + O(3)

Vereinfachend erhalten wir:

O(8) + O(2n) = O(8+2n)

Wir haben bereits gesagt, dass wenn die Eingabe (die in diesem Fall die Länge n hat) extrem groß wird, die Konstanten unbedeutend werden, dh das Zweifache oder die Hälfte von Unendlich bleibt immer noch Unendlich. Daher können wir die Konstanten ignorieren. Die endgültige Komplexität des Algorithmus wird sein O (n)!

Komplexität des schlimmsten vs. besten Falls

Wenn Sie jemand nach der Komplexität eines Algorithmus fragt, interessiert er sich normalerweise für die Worst-Case-Komplexität (Big-O). Manchmal interessieren sie sich auch für die Komplexität im besten Fall (Big-Omega).

Um die Beziehung zwischen diesen zu verstehen, werfen wir einen Blick auf ein anderes Stück Code:

def search_algo(num, items):
    for item in items:
        if item == num:
            return True
        else:
            pass
nums = [2, 4, 6, 8, 10]

print(search_algo(2, nums))

Im obigen Skript haben wir eine Funktion, die eine Zahl und eine Liste von Zahlen als Eingabe akzeptiert. Es gibt true zurück, wenn die übergebene Zahl in der Liste der Zahlen gefunden wird, andernfalls wird es zurückgegeben None. Wenn Sie in der Liste nach 2 suchen, wird es im ersten Vergleich gefunden. Dies ist die beste Fallkomplexität des Algorithmus, da das gesuchte Element im ersten gesuchten Index gefunden wird. Die beste Fallkomplexität, ist in diesem Fall O (1). Wenn Sie dagegen nach 10 suchen, wird es im zuletzt durchsuchten Index gefunden. Der Algorithmus muss daher alle Elemente in der Liste durchsuchen die Worst-Case-Komplexität wird O (n).

Neben Best- und Worst-Case-Komplexität können Sie auch rechnen die durchschnittliche Komplexität (Big-Theta) eines Algorithmus, der Ihnen sagt, „was ist die erwartete Zeitkomplexität des Algorithmus bei einer zufälligen Eingabe“?

Raumkomplexität

Neben der Zeitkomplexität, bei der Sie die Anzahl der Schritte zählen, die erforderlich sind, um die Ausführung eines Algorithmus abzuschließen, finden Sie auch die Raumkomplexität Dies bezieht sich auf die Menge an Speicherplatz, die Sie während der Ausführung eines Programms im Speicher zuweisen müssen.

Schauen Sie sich das folgende Beispiel an:

def return_squares(n):
    square_list = []
    for num in n:
        square_list.append(num * num)

    return square_list

nums = [2, 4, 6, 8, 10]
print(return_squares(nums))

Das return_squares() Die Funktion akzeptiert eine Liste von ganzen Zahlen und gibt eine Liste mit den entsprechenden Quadraten zurück. Der Algorithmus muss Speicher für dieselbe Anzahl von Elementen wie in der Eingabeliste zuweisen. Daher wird die Raumkomplexität des Algorithmus O (n).

Zusammenfassung

Die Big-O-Notation ist die Standardmetrik, die verwendet wird, um die Komplexität eines Algorithmus zu messen. In diesem Leitfaden haben wir untersucht, was die Big-O-Notation ist und wie sie verwendet werden kann, um die Komplexität einer Vielzahl von Algorithmen zu messen. Wir haben auch verschiedene Arten von Big-O-Funktionen mit Hilfe verschiedener Python-Beispiele untersucht. Abschließend haben wir kurz die Worst- und Best-Case-Komplexität zusammen mit der Raumkomplexität überprüft.