1Zapata Computing, Inc., 100 Federal Street, 20th Floor, Boston, Massachusetts 02110, USA
2Harvard University
3Institut für Hochleistungsrechnen, Agentur für Wissenschaft, Technologie und Forschung (A*STAR), 1 Fusionopolis Way, #16-16 Connexis, Singapur 138632, Singapur
Findest du dieses Paper interessant oder möchtest du darüber diskutieren? Scite oder hinterlasse einen Kommentar zu SciRate.
Abstrakt
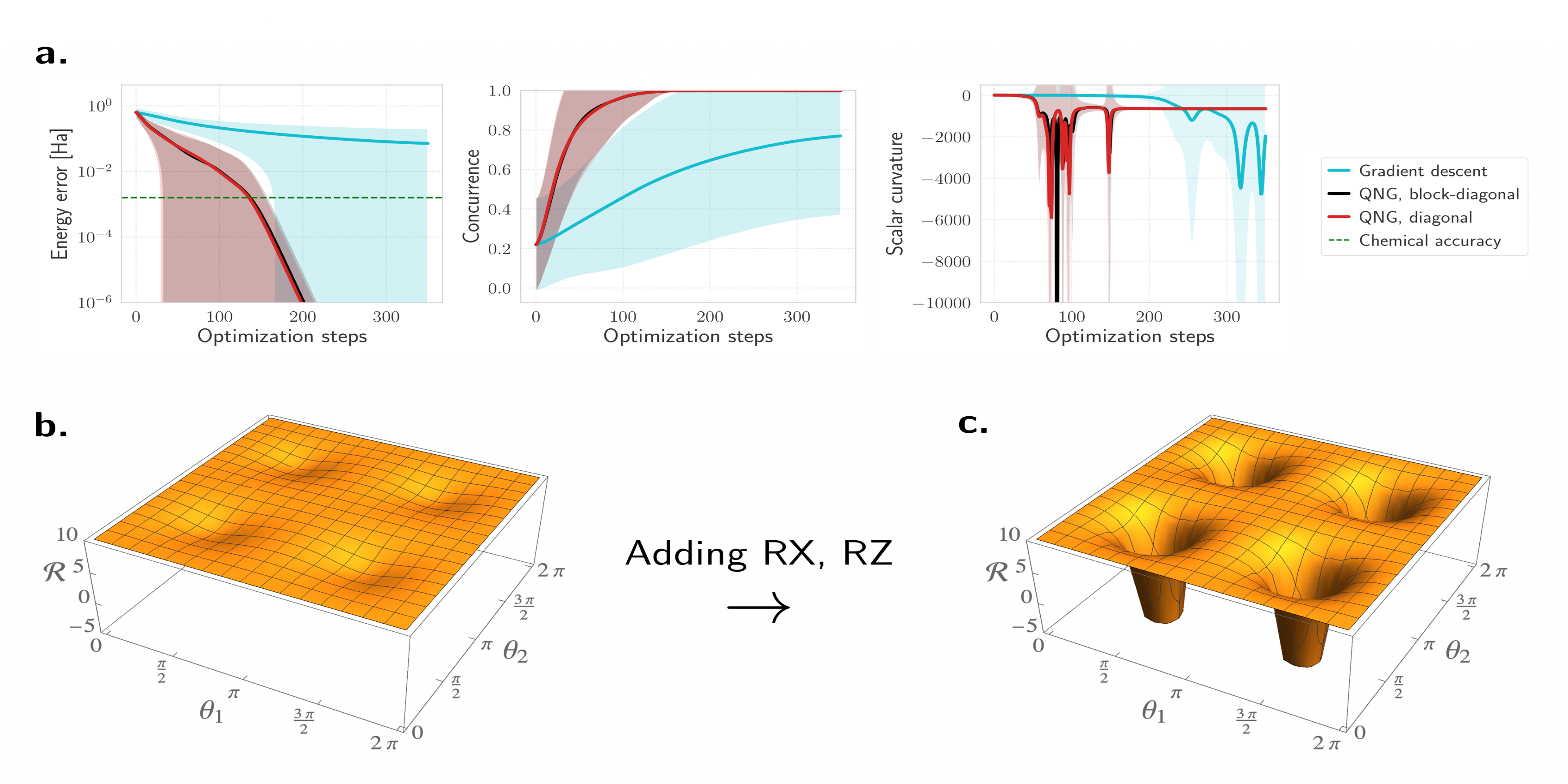
Parametrisierte Quantenschaltkreise (PQCs) sind eine zentrale Komponente vieler Variations-Quantenalgorithmen, jedoch fehlt es an Verständnis dafür, wie sich ihre Parametrisierung auf die Leistung von Algorithmen auswirkt. Wir leiten diese Diskussion ein, indem wir Hauptbündel verwenden, um Zwei-Qubit-PQCs geometrisch zu charakterisieren. Auf der Basismannigfaltigkeit verwenden wir die Metrik der Mannoury-Fubini-Studie, um eine einfache Gleichung zu finden, die den Ricci-Skalar (Geometrie) und die Übereinstimmung (Verschränkung) in Beziehung setzt. Durch die Berechnung des Ricci-Skalars während eines Variational Quantum Eigensolver (VQE)-Optimierungsprozesses bietet uns dies eine neue Perspektive, wie und warum Quantum Natural Gradient den Standard-Gradientenabstieg übertrifft. Wir argumentieren, dass der Schlüssel zur überlegenen Leistung des Quantum Natural Gradient in seiner Fähigkeit liegt, Regionen mit stark negativer Krümmung früh im Optimierungsprozess zu finden. Diese Bereiche mit hoher negativer Krümmung scheinen wichtig zu sein, um den Optimierungsprozess zu beschleunigen.
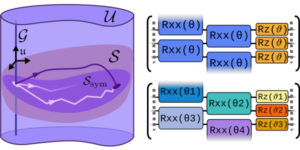
Ausgewähltes Bild: Das Hinzufügen einzelner Qubit-Gatter ermöglicht es dem Quantum Natural-Gradienten, Orte mit negativer Ricci-Krümmung zu finden. Beachten Sie, dass wir zuvor den verschränkten Grundzustand nicht finden konnten und daher das Hinzufügen einzelner Qubit-Gatter die Verschränkungseigenschaften des Ansatzes nicht ändert und ihre Hinzufügung es uns dennoch ermöglichte, einen verschränkten Zustand zu finden, den wir zuvor nicht finden konnten; Wir argumentieren, dass sich die Geometrie geändert hat.
[Eingebetteten Inhalt]
Populäre Zusammenfassung
► BibTeX-Daten
► Referenzen
[1] Marco Cerezo, Andrew Arrasmith, Ryan Babbush, Simon C. Benjamin, Suguru Endo, Keisuke Fujii, Jarrod R. McClean, Kosuke Mitarai, Xiao Yuan, Lukasz Cincio, et al. Variationelle Quantenalgorithmen. Nature Reviews Physics, 3:625–644, 2021. 10.1038/s42254-021-00348-9.
https://doi.org/10.1038/s42254-021-00348-9
[2] Kishor Bharti, Alba Cervera-Lierta, Thi Ha Kyaw, Tobias Haug, Sumner Alperin-Lea, Abhinav Anand, Matthias Degroote, Hermanni Heimonen, Jakob S. Kottmann, Tim Menke, Wai-Keong Mok, Sukin Sim, Leong-Chuan Kwek, und Alán Aspuru-Guzik. Verrauschte Quantenalgorithmen im mittleren Maßstab. Rev. Mod. Phys., 94:015004, Februar 2022. 10.1103/RevModPhys.94.015004.
https: / / doi.org/ 10.1103 / RevModPhys.94.015004
[3] M.-H. Yung, J. Casanova, A. Mezzacapo, J. McClean, L. Lamata, A. Aspuru-Guzik und E. Solano. Vom Transistor- zum Trapped-Ion-Computer für die Quantenchemie. Wissenschaft. Rep, 4:3589, Mai 2015. 10.1038/srep03589.
https: / / doi.org/ 10.1038 / srep03589
[4] Yudong Cao, Jonathan Romero, Jonathan P. Olson, Matthias Degroote, Peter D. Johnson, Mária Kieferová, Ian D. Kivlichan, Tim Menke, Borja Peropadre, Nicolas PD Sawaya, Sukin Sim, Libor Veis und Alán Aspuru-Guzik. Quantenchemie im Zeitalter des Quantencomputings. Chemical Reviews, 119(19):10856–10915, Okt. 2019. 10.1021/acs.chemrev.8b00803.
https: // doi.org/ 10.1021 / acs.chemrev.8b00803
[5] Abhinav Anand, Philipp Schleich, Sumner Alperin-Lea, Phillip WK Jensen, Sukin Sim, Manuel Díaz-Tinoco, Jakob S. Kottmann, Matthias Degroote, Artur F. Izmaylov und Alán Aspuru-Guzik. Ein Quantencomputing-Blick auf die Unitary Coupled Cluster Theory. Chem. Soc. Rev., 51:1659–1684, März 2022. 10.1039/D1CS00932J.
https:///doi.org/10.1039/D1CS00932J
[6] Vojtěch Havlíček, Antonio D. Córcoles, Kristan Temme, Aram W. Harrow, Abhinav Kandala, Jerry M. Chow und Jay M. Gambetta. Überwachtes Lernen mit quantenerweiterten Funktionsräumen. Nature, 567:209–212, März 2019. 10.1038/s41586-019-0980-2.
https://doi.org/10.1038/s41586-019-0980-2
[7] Abhinav Kandala, Antonio Mezzacapo, Kristan Temme, Maika Takita, Markus Brink, Jerry M. Chow und Jay M. Gambetta. Hardwareeffizienter Variations-Quanten-Eigenlöser für kleine Moleküle und Quantenmagnete. Nature, 549:242–246, Sept. 2017. 10.1038/nature23879.
https: / / doi.org/ 10.1038 / nature23879
[8] Stig Elkjær Rasmussen, Niels Jakob Søe Loft, Thomas Bækkegaard, Michael Kues und Nikolaj Thomas Zinner. Verringerung der Anzahl von Einzel-Qubit-Rotationen in VQE und verwandten Algorithmen. Advanced Quantum Technologies, 3(12):2000063, Dez 2020. 10.1002/qute.202000063.
https: / / doi.org/ 10.1002 / qute.202000063
[9] Sukin Sim, Jonathan Romero, Jérôme F. Gonthier und Alexander A. Kunitsa. Adaptive Pruning-basierte Optimierung parametrisierter Quantenschaltkreise. Quantum Science and Technology, 6(2):025019, April 2021. 10.1088/2058-9565/abe107.
https: / / doi.org/ 10.1088 / 2058-9565 / abe107
[10] Lena Funcke, Tobias Hartung, Karl Jansen, Stefan Kühn und Paolo Stornati. Dimensionale Expressivitätsanalyse von parametrischen Quantenschaltkreisen. Quantum, 5:422, März 2021. 10.22331/q-2021-03-29-422.
https://doi.org/10.22331/q-2021-03-29-422
[11] Jarrod R. McClean, Sergio Boixo, Vadim N. Smelyanskiy, Ryan Babbush und Hartmut Neven. Karge Plateaus in Trainingslandschaften für quantenneuronale Netze. Nat. Commun, 9:4812, 2018. 10.1038/s41467-018-07090-4.
https://doi.org/10.1038/s41467-018-07090-4
[12] Andrew Arrasmith, Zoë Holmes, M. Cerezo und Patrick J. Coles. Äquivalenz von quantenödlichen Plateaus zu Kostenkonzentration und engen Schluchten. Quantum Science and Technology, 7(4):045015, Aug. 2022. 10.1088/2058-9565/ac7d06.
https://doi.org/10.1088/2058-9565/ac7d06
[13] Sukin Sim, Peter D. Johnson und Alán Aspuru-Guzik. Ausdrückbarkeit und Verschränkungsfähigkeit parametrisierter Quantenschaltkreise für hybride quantenklassische Algorithmen. Advanced Quantum Technologies, 2(12):1900070, 2019. 10.1002/qute.201900070.
https: / / doi.org/ 10.1002 / qute.201900070
[14] Thomas Hubregtsen, Josef Pichlmeier, Patrick Stecher und Koen Bertels. Evaluation parametrisierter Quantenschaltkreise: Zum Zusammenhang zwischen Klassifikationsgenauigkeit, Ausdrückbarkeit und Verschränkungsfähigkeit. Quantum Machine Intelligence, 3:9, 2021. 10.1007/s42484-021-00038-w.
https: / / doi.org/ 10.1007 / s42484-021-00038-w
[15] Zoë Holmes, Kunal Sharma, M. Cerezo und Patrick J. Coles. Verbindung von Ansatz-Ausdrückbarkeit mit Gradientengrößen und unfruchtbaren Plateaus. PRX Quantum, 3:010313, Januar 2022. 10.1103/PRXQuantum.3.010313.
https: / / doi.org/ 10.1103 / PRXQuantum.3.010313
[16] James Stokes, Josh Izaac, Nathan Killoran und Giuseppe Carleo. Quantennatürlicher Gradient. Quantum, 4:269, 2020. 10.22331/q-2020-05-25-269.
https://doi.org/10.22331/q-2020-05-25-269
[17] Tobias Haug, Kishor Bharti und MS Kim. Kapazität und Quantengeometrie parametrisierter Quantenschaltkreise. PRX Quantum, 2:040309, Okt. 2021. 10.1103/PRXQuantum.2.040309.
https: / / doi.org/ 10.1103 / PRXQuantum.2.040309
[18] Tobias Haug und MS Kim. Optimales Training von Variations-Quantenalgorithmen ohne öde Plateaus. arXiv-Vorabdruck arXiv:2104.14543, 2021. 10.48550/arXiv.2104.14543.
https:///doi.org/10.48550/arXiv.2104.14543
arXiv: 2104.14543
[19] Tyson Jones. Effiziente klassische Berechnung des natürlichen Quantengradienten. arXiv-Vordruck arXiv:2011.02991, 2020. 10.48550/arXiv.2011.02991.
https:///doi.org/10.48550/arXiv.2011.02991
arXiv: 2011.02991
[20] Barnaby van Straaten und Bálint Koczor. Messkosten von metrikbewussten Variationsquantenalgorithmen. PRX Quantum, 2:030324, August 2021. 10.1103/PRXQuantum.2.030324.
https: / / doi.org/ 10.1103 / PRXQuantum.2.030324
[21] Bálint Koczor und Simon C. Benjamin. Natürlicher Quantengradient verallgemeinert auf nicht-einheitliche Schaltkreise. arXiv-Vorabdruck arXiv:1912.08660, 2019. 10.48550/arXiv.1912.08660.
https:///doi.org/10.48550/arXiv.1912.08660
arXiv: 1912.08660
[22] Hoshang Heydari. Geometrische Formulierung der Quantenmechanik. arXiv-Vordruck arXiv:1503.00238, 2015. 10.48550/arXiv.1503.00238.
https:///doi.org/10.48550/arXiv.1503.00238
arXiv: 1503.00238
[23] Robert Geroch. Robert Geroch, Geometrische Quantenmechanik: 1974 Vorlesungsnotizen. Minkowski Institute Press, Montreal 2013, 2013.
[24] Ran Cheng. Quantengeometrischer Tensor (Fubini-Studienmetrik) im einfachen Quantensystem: Eine pädagogische Einführung. arXiv-Vorabdruck arXiv:1012.1337, 2010. 10.48550/arXiv.1012.1337.
https:///doi.org/10.48550/arXiv.1012.1337
arXiv: 1012.1337
[25] Jutho Haegeman, Michaël Marien, Tobias J. Osborne und Frank Verstraete. Geometrie der Matrixproduktzustände: Metrisch, paralleler Transport und Krümmung. J. Math. Phys, 55(2):021902, 2014. 10.1063/1.4862851.
https: / / doi.org/ 10.1063 / 1.4862851
[26] Naoki Yamamoto. Über den natürlichen Gradienten für Variations-Quanten-Eigenlöser. arXiv-Vorabdruck arXiv:1909.05074, 2019. 10.48550/arXiv.1909.05074.
https:///doi.org/10.48550/arXiv.1909.05074
arXiv: 1909.05074
[27] Pierre-Luc Dallaire-Demers, Jonathan Romero, Libor Veis, Sukin Sim und Alán Aspuru-Guzik. Low-Tiefe Schaltungsansatz zur Präparation korrelierter fermionischer Zustände auf einem Quantencomputer. Quantenwissenschaft. Technol, 4(4):045005, Sept. 2019. 10.1088/2058-9565/ab3951.
https: / / doi.org/ 10.1088 / 2058-9565 / ab3951
[28] Pierre-Luc Dallaire-Demers und Nathan Killoran. Quantengenerative gegnerische Netzwerke. Phys. Rev. A, 98:012324, Juli 2018. 10.1103/PhysRevA.98.012324.
https: / / doi.org/ 10.1103 / PhysRevA.98.012324
[29] Pierre-Luc Dallaire-Demers, Michał Stęchły, Jerome F. Gonthier, Ntwali Toussaint Bashige, Jonathan Romero und Yudong Cao. Ein Anwendungsbenchmark für fermionische Quantensimulationen. arXiv Vorabdruck arXiv:2003.01862, 2020. 10.48550/arXiv.2003.01862.
https:///doi.org/10.48550/arXiv.2003.01862
arXiv: 2003.01862
[30] Frank Arute, Kunal Arya, Ryan Babbush, Dave Bacon, Joseph C. Bardin, Rami Barends, Rupak Biswas, Sergio Boixo, Fernando GSL Brandao, David A. Buell, et al. Quantenüberlegenheit mit einem programmierbaren supraleitenden Prozessor. Nature, 574:505–510, 2019. 10.1038/s41586-019-1666-5.
https://doi.org/10.1038/s41586-019-1666-5
[31] Chu-Ryang Wie. Zwei-Qubit-Bloch-Sphäre. Physik, 2(3):383–396, 2020. 10.3390/physics2030021.
https:///doi.org/10.3390/physics2030021
[32] Peter Levay. Die Geometrie der Verschränkung: Metriken, Verbindungen und die geometrische Phase. Journal of Physics A: Mathematical and General, 37(5):1821–1841, Jan 2004. 10.1088/0305-4470/37/5/024.
https://doi.org/10.1088/0305-4470/37/5/024
[33] James Martens und Roger Grosse. Optimierung neuronaler Netze mit Kronecker-faktorisierter ungefährer Krümmung. In Francis Bach und David Blei, Herausgeber, Proceedings of the 32nd International Conference on Machine Learning, Band 37 von Proceedings of Machine Learning Research, Seiten 2408–2417, Lille, Frankreich, 07.–09. Juli 2015. PMLR.
[34] Alberto Bernacchia, Máté Lengyel und Guillaume Hennequin. Exakter natürlicher Gradient in tiefen linearen Netzwerken und Anwendung auf den nichtlinearen Fall. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, NIPS'18, Seite 5945–5954, Red Hook, NY, USA, 2018. Curran Associates Inc.
[35] Sam A. Hill und William K. Wootters. Verschränkung eines Paares von Quantenbits. Phys. Rev. Lett., 78:5022–5025, Juni 1997. 10.1103/PhysRevLett.78.5022.
https://doi.org/ 10.1103/PhysRevLett.78.5022
[36] Li Chen, Ming Yang, Li-Hua Zhang und Zhuo-Liang Cao. Direktes Messen der Gleichzeitigkeit des Zwei-Atom-Zustands durch Detektion von kohärentem Licht. Laser-Phys. Lett., 14(11):115205, Okt. 2017. 10.1088/1612-202X/aa8582.
https:///doi.org/10.1088/1612-202X/aa8582
[37] Lan Zhou und Yu-Bo Sheng. Gleichzeitigkeitsmessung für die optischen und atomaren Zwei-Qubit-Zustände. Entropy, 17(6):4293–4322, 2015. 10.3390/e17064293.
https: / / doi.org/ 10.3390 / e17064293
[38] Sean M. Caroll. Raumzeit und Geometrie: Eine Einführung in die Allgemeine Relativitätstheorie. Cambridge University Press, 2019. 10.1017/9781108770385.
https: / / doi.org/ 10.1017 / 9781108770385
[39] Anshuman Dey, Subhash Mahapatra, Pratim Roy und Tapobrata Sarkar. Informationsgeometrie und Quantenphasenübergänge im Dicke-Modell. Phys. Rev. E, 86(3):031137, Sept. 2012. 10.1103/PhysRevE.86.031137.
https: / / doi.org/ 10.1103 / PhysRevE.86.031137
[40] Rıza Erdem. Quantengittermodell mit lokalen Multi-Well-Potentialen: Riemannsche geometrische Interpretation für die Phasenübergänge in ferroelektrischen Kristallen. Physica A: Statistical Mechanics and its Applications, 556:124837, 2020. 10.1016/j.physa.2020.124837.
https: / / doi.org/ 10.1016 / j.physa.2020.124837
[41] Michael Kolodrubetz, Vladimir Gritsev und Anatoli Polkovnikov. Klassifizierung und Messung der Geometrie einer Quanten-Grundzustands-Mannigfaltigkeit. Phys. Rev. B, 88:064304, August 2013. 10.1103/PhysRevB.88.064304.
https://doi.org/ 10.1103/PhysRevB.88.064304
[42] Michael Hauser und Asok Ray. Prinzipien der Riemannschen Geometrie in neuronalen Netzen. In I. Guyon, UV Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan und R. Garnett, Herausgeber, Advances in Neural Information Processing Systems, Band 30. Curran Associates, Inc., 2017.
[43] T. Yu, H. Long und JE Hopcroft. Krümmungsbasierter Vergleich zweier neuronaler Netze. In 2018 24th International Conference on Pattern Recognition (ICPR), Seiten 441–447, 2018. 10.1109/ICPR.2018.8546273.
https:///doi.org/10.1109/ICPR.2018.8546273
[44] P. Kaul und B. Lall. Riemannsche Krümmung tiefer neuronaler Netze. IEEE-Trans. Neuronales Netz Lernen. Syst., 31(4):1410–1416, 2020. 10.1109/TNNLS.2019.2919705.
https:///doi.org/10.1109/TNNLS.2019.2919705
[45] Alberto Peruzzo, Jarrod McClean, Peter Shadbolt, Man-Hong Yung, Xiao-Qi Zhou, Peter J. Love, Alán Aspuru-Guzik und Jeremy L. O'Brien. Ein Variations-Eigenwertlöser auf einem photonischen Quantenprozessor. Nat. Commun, 5:4213, Sept. 2014. 10.1038/ncomms5213.
https: / / doi.org/ 10.1038 / ncomms5213
[46] Peter JJ O’Malley, Ryan Babbush, Ian D. Kivlichan, Jonathan Romero, Jarrod R. McClean, Rami Barends, Julian Kelly, Pedram Roushan, Andrew Tranter, Nan Ding, et al. Skalierbare Quantensimulation molekularer Energien. Physical Review X, 6(3):031007, 2016. 10.1103/PhysRevX.6.031007.
https://doi.org/ 10.1103/PhysRevX.6.031007
[47] John Frank Adams. Über die Nichtexistenz von Elementen der Hopf-Invariante. Stier. Bin. Mathematik. Soc, 64(5):279–282, 1958.
[48] Shreyas Bapat, Ritwik Saha, Bhavya Bhatt, Hrushikesh Sarode, Gaurav Kumar und Priyanshu Khandelwal. einsteinpy/einsteinpy: EinsteinPy 0.1a1 (Alpha Release – 1), März 2019. 10.5281/zenodo.2582388.
https: / / doi.org/ 10.5281 / zenodo.2582388
[49] Wolfram Research, Inc. Mathematica, Version 12.0. Champaign, Illinois, 2019.
[50] Jarrod R. McClean, Nicholas C. Rubin, Kevin J. Sung, Ian D. Kivlichan, Xavier Bonet-Monroig, Yudong Cao, Chengyu Dai, E. Schuyler Fried, Craig Gidney, Brendan Gimby, et al. Openfermion: das elektronische Strukturpaket für Quantencomputer. Quantum Science and Technology, 5(3):034014, 2020. 10.1088/2058-9565/ab8ebc.
https: / / doi.org/ 10.1088 / 2058-9565 / ab8ebc
[51] Ville Bergholm, Josh Izaac, Maria Schuld, Christian Gogolin, Shahnawaz Ahmed, Vishnu Ajith, M. Sohaib Alam, Guillermo Alonso-Linaje, B. AkashNarayanan, Ali Asadi, et al. Pennylane: Automatische Differenzierung hybrider quantenklassischer Berechnungen. arXiv-Vorabdruck arXiv:1811.04968, 2018. 10.48550/arXiv.1811.04968.
https:///doi.org/10.48550/arXiv.1811.04968
arXiv: 1811.04968
Zitiert von
[1] Tobias Haug und MS Kim, „Natürliche parametrisierte Quantenschaltung“, arXiv: 2107.14063.
[2] Francesco Scala, Stefano Mangini, Chiara Macchiavello, Daniele Bajoni und Dario Gerace, „Quantum Variational Learning for Entanglement Witnessing“, arXiv: 2205.10429.
[3] Roeland Wiersema und Nathan Killoran, „Optimierung von Quantenschaltkreisen mit Riemannschem Gradientenfluss“, arXiv: 2202.06976.
Die obigen Zitate stammen von SAO / NASA ADS (Zuletzt erfolgreich aktualisiert am 2022, 08:26:00 Uhr). Die Liste ist möglicherweise unvollständig, da nicht alle Verlage geeignete und vollständige Zitationsdaten bereitstellen.
On Der von Crossref zitierte Dienst Es wurden keine Daten zum Zitieren von Werken gefunden (letzter Versuch 2022-08-26 00:47:30).
Dieses Papier ist in Quantum unter dem veröffentlicht Creative Commons Namensnennung 4.0 International (CC BY 4.0) Lizenz. Das Copyright verbleibt bei den ursprünglichen Copyright-Inhabern wie den Autoren oder deren Institutionen.