1Institut-Lorentz, Universität Leiden, 2300 RA Leiden, Niederlande
2QuTech, Technische Universität Delft, Postfach 5046, 2600 GA Delft, Niederlande und JARA Institute for Quantum Information, Forschungszentrum Jülich, D-52425 Jülich, Deutschland
3Google Quantum AI, 80636 München, Deutschland
Findest du dieses Paper interessant oder möchtest du darüber diskutieren? Scite oder hinterlasse einen Kommentar zu SciRate.
Abstrakt
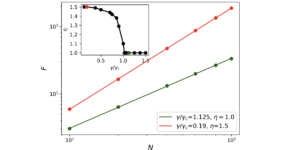
Die Quantenphasenschätzung ist ein Eckpfeiler im Design von Quantenalgorithmen, die die Ableitung von Eigenwerten von exponentiell großen dünn besetzten Matrizen ermöglicht. Die maximale Rate, mit der diese Eigenwerte gelernt werden können, bekannt als Heisenberg-Grenze, wird durch Grenzen auf der Schaltung eingeschränkt Komplexität, die erforderlich ist, um einen beliebigen Hamilton-Operator zu simulieren. Single-Control-Qubit-Varianten der Quantenphasenschätzung, die keine Kohärenz zwischen den Experimenten erfordern, haben in den letzten Jahren aufgrund der geringeren Schaltungstiefe und des minimalen Qubit-Overheads Interesse geweckt. In dieser Arbeit zeigen wir, dass diese Methoden die Heisenberg-Grenze erreichen können, $auch$ wenn man keine Eigenzustände des Systems präparieren kann. Gegeben sei eine Quanten-Subroutine, die Proben einer `Phasenfunktion' $g(k)=sum_j A_j e^{i phi_j k}$ mit unbekannten Eigenphasen $phi_j$ liefert und $A_j$ bei Quantenkosten $O(k)$ überlappt, wir zeigen, wie man die Phasen ${phi_j}$ mit dem (root-mean-square) Fehler $delta$ für die Gesamtquantenkosten $T=O(delta^{-1})$ schätzt. Unser Schema kombiniert die Idee der Heisenberg-begrenzten Quantenphasenschätzung mehrerer Ordnungen für eine einzelne Eigenwertphase [Higgins et al (2009) und Kimmel et al (2015)] mit Unterroutinen mit sogenannter dichter Quantenphasenschätzung, die klassische Verarbeitung über verwendet Zeitreihenanalyse für das QEEP-Problem [Somma (2019)] oder die Matrix-Pencil-Methode. Für unseren Algorithmus, der die Wahl für $k$ in $g(k)$ adaptiv festlegt, beweisen wir die Heisenberg-begrenzte Skalierung, wenn wir die Time-Series/QEEP-Subroutine verwenden. Wir präsentieren numerische Beweise dafür, dass der Algorithmus unter Verwendung der Matrix-Pencil-Technik auch eine Heisenberg-begrenzte Skalierung erreichen kann.
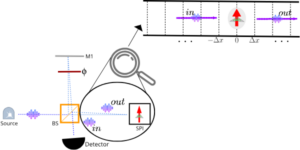
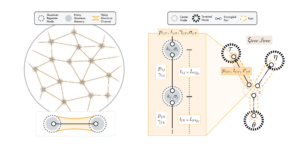
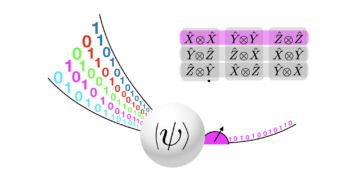
Ausgewähltes Bild: Ein Heisenberg-begrenztes Schema zur Erkennung mehrerer Phasen $phi_j$. Zuerst wird eine anfängliche Schätzung von $phi_jin[0,2pi]$ aus einer Zeitreihe ${langle Urangle, langle U^2rangle ldots}$ vorgenommen. Dann wird eine Schätzung von $kphi_j$ für einige $k>1$ vorgenommen, wobei ${langle U^{k}rangle, langle U^{2k}rangle,ldots }$ verwendet werden. Dies erzeugt eine genauere Schätzung von $phi_j$ (kleinere Fehlerbalken), aber modulo $2pi/k$. Daten aus der ersten Schätzung werden verwendet, um diese Schätzung zu stabilisieren und unerwünschte Aliase (gestrichelte Linien) zu entfernen. Dies wird für immer größere Werte von $k$ wiederholt, um die Heisenberg-Grenze zu erreichen. Der Multiplikator $k$ wird basierend auf den vorherigen Schätzungen gewählt, um eine eindeutige Schätzung zu ermöglichen.
Populäre Zusammenfassung
► BibTeX-Daten
► Referenzen
[1] BL Higgins, DW Berry, SD Bartlett, MW Mitchell, HM Wiseman und GJ Pryde. Demonstration der Heisenberg-begrenzten eindeutigen Phasenschätzung ohne adaptive Messungen. New J. Phys., 11 (7): 073023, 2009. 10.1088/1367-2630/11/7/073023. URL https:///arxiv.org/abs/0809.3308.
https://doi.org/10.1088/1367-2630/11/7/073023
arXiv: 0809.3308
[2] Shelby Kimmel, Guang Hao Low und Theodore J. Yoder. Robuste Kalibrierung eines universellen Single-Qubit-Gate-Sets über robuste Phasenschätzung. Phys. Rev. A, 92: 062315, 2015. 10.1103/PhysRevA.92.062315. URL https:///arxiv.org/abs/1502.02677.
https: / / doi.org/ 10.1103 / PhysRevA.92.062315
arXiv: 1502.02677
[3] Rolando D. Somma. Quanteneigenwertschätzung durch Zeitreihenanalyse. New J. Phys., 21: 123025, 2019. 10.1088/1367-2630/ab5c60. URL https:///iopscience.iop.org/article/10.1088/1367-2630/ab5c60/pdf.
https://doi.org/10.1088/1367-2630/ab5c60
[4] Pawel Wocjan und Shengyu Zhang. Mehrere natürliche BQP-vollständige Probleme. ArXiv:quant-ph/0606179, 2006. 10.48550/arXiv.quant-ph/0606179. URL https:///arxiv.org/abs/quant-ph/0606179.
https:///doi.org/10.48550/arXiv.quant-ph/0606179
arXiv: quant-ph / 0606179
[5] Peter W. Shor. Polynomzeitalgorithmen zur Primfaktorzerlegung und diskreten Logarithmen auf einem Quantencomputer. SIAM J. Sci. Stat. Comp., 26: 1484, 1997. 10.1137/S0097539795293172. URL https:///arxiv.org/abs/quant-ph/9508027.
https: / / doi.org/ 10.1137 / S0097539795293172
arXiv: quant-ph / 9508027
[6] Aram W. Harrow, Avinatan Chassidim und Seth Lloyd. Quantenalgorithmus zum Lösen linearer Gleichungssysteme. Phys. Rev. Lett., 15 (103): 150502, 2009. 10.1103/PhysRevLett.103.150502. URL https:///arxiv.org/abs/0811.3171.
https://doi.org/ 10.1103/PhysRevLett.103.150502
arXiv: 0811.3171
[7] James D. Whitfield, Jacob Biamonte und Alán Aspuru-Guzik. Simulation elektronischer Struktur-Hamiltonianer mit Quantencomputern. Mol. Phys., 109: 735–750, 2011. 10.1080/00268976.2011.552441. URL https:///arxiv.org/abs/1001.3855.
https: / / doi.org/ 10.1080 / 00268976.2011.552441
arXiv: 1001.3855
[8] MA Nielsen und IL Chuang. Quantencomputation und Quanteninformation. Cambridge Series on Information and the Natural Sciences. Cambridge University Press, 2000. ISBN 9780521635035. 10.1017/CBO9780511976667. URL https:///books.google.de/books?id=65FqEKQOfP8C.
https: / / doi.org/ 10.1017 / CBO9780511976667
https:///books.google.de/books?id=65FqEKQOfP8C
[9] R. Cleve, A. Ekert, C. Macchiavello und M. Mosca. Quantenalgorithmen neu aufgelegt. Verfahren der Royal Society of London. Serie A: Mathematical, Physical and Engineering Sciences, 454 (1969): 339–354, 1998. 10.1098/rspa.1998.0164. URL https:///royalsocietypublishing.org/doi/abs/10.1098/rspa.1998.0164.
https: / / doi.org/ 10.1098 / rspa.1998.0164
[10] Vittorio Giovannetti, Seth Lloyd und Lorenzo Maccone. Quantenmetrologie. Physical Review Letters, 96 (1): 010401, 2006. 10.1103/PhysRevLett.96.010401. URL https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.96.010401.
https://doi.org/ 10.1103/PhysRevLett.96.010401
[11] Wim van Dam, G. Mauro D’Ariano, Artur Ekert, Chiara Macchiavello und Michele Mosca. Optimale Quantenschaltkreise für die allgemeine Phasenschätzung. Phys. Rev. Lett., 98: 090501, März 2007. 10.1103/PhysRevLett.98.090501. URL https://link.aps.org/doi/10.1103/PhysRevLett.98.090501.
https://doi.org/ 10.1103/PhysRevLett.98.090501
[12] Dominic W. Berry, Brendon L. Higgins, Stephen D. Bartlett, Morgan W. Mitchell, Geoff J. Pryde und Howard M. Wiseman. So führen Sie möglichst genaue Phasenmessungen durch. Physical Review A, 80 (5): 052114, 2009. 10.1103/PhysRevA.80.052114.
https: / / doi.org/ 10.1103 / PhysRevA.80.052114
[13] Robert B. Griffiths und Chi-Sheng Niu. Semiklassische Fourier-Transformation für die Quantenberechnung. Physical Review Letters, 76 (17): 3228–3231, April 1996. ISSN 1079-7114. 10.1103/physrevlett.76.3228. URL 10.1103/PhysRevLett.76.3228.
https://doi.org/ 10.1103/physrevlett.76.3228
http:///10.1103/PhysRevLett.76.3228
[14] A. Ju. Kitaev. Quantenmessungen und das Abelsche Stabilisatorproblem. ArXiv:quant-ph/9511026, 1995. 10.48550/arXiv.quant-ph/9511026. URL https:///arxiv.org/abs/quant-ph/9511026.
https:///doi.org/10.48550/arXiv.quant-ph/9511026
arXiv: quant-ph / 9511026
[15] Dominic W. Berry, Graeme Ahokas, Richard Cleve und Barry C. Sanders. Effiziente Quantenalgorithmen zur Simulation von Sparse-Hamiltonoperatoren. Komm. Mathematik. Phys., 270 (359), 2007. 10.1007/s00220-006-0150-x. URL https:///arxiv.org/abs/quant-ph/0508139.
https: / / doi.org/ 10.1007 / s00220-006-0150-x
arXiv: quant-ph / 0508139
[16] Nathan Wiebe und Chris Granade. Effiziente bayessche Phasenschätzung. Phys. Rev. Lett., 117: 010503, 2016. 10.1103/PhysRevLett.117.010503. URL https:///arxiv.org/abs/1508.00869.
https://doi.org/ 10.1103/PhysRevLett.117.010503
arXiv: 1508.00869
[17] Krysta M. Svore, Matthew B. Hastings und Michael Freedman. Schnellere Phasenschätzung. Menge Inf. Comp., 14 (3-4): 306–328, 2013. 10.48550/arXiv.1304.0741. URL https:///arxiv.org/abs/1304.0741.
https:///doi.org/10.48550/arXiv.1304.0741
arXiv: 1304.0741
[18] Ewout van den Berg. Effiziente bayessche Phasenschätzung mit gemischten Prioren. ArXiv:2007.11629, 2020. 10.22331/q-2021-06-07-469. URL https:///arxiv.org/abs/2007.11629.
https://doi.org/10.22331/q-2021-06-07-469
arXiv: 2007.11629
[19] Thomas E. O'Brien, Brian Tarasinski und Barbara M. Terhal. Quantenphasenschätzung mehrerer Eigenwerte für kleine (verrauschte) Experimente. New J. Phys., 21: 023022, 2019. 10.1088/1367-2630/aafb8e. URL https:///iopscience.iop.org/article/10.1088/1367-2630/aafb8e.
https:///doi.org/10.1088/1367-2630/aafb8e
[20] David C. Rife und Robert R. Boorstyn. Einzeltonparameterschätzung aus zeitdiskreten Beobachtungen. IEEE-Trans. Inf. Th., 20 (5): 591–598, 1974. 10.1109/TIT.1974.1055282. URL https:///ieeexplore.ieee.org/document/1055282.
https: / / doi.org/ 10.1109 / TIT.1974.1055282
https: / / ieeexplore.ieee.org/ document / 1055282
[21] Sirui Lu, Mari Carmen Bañuls und J. Ignacio Cirac. Algorithmen zur Quantensimulation bei endlichen Energien. PRX Quantum, 2: 020321, 2020. 10.1103/PRXQuantum.2.020321. URL https://journals.aps.org/prxquantum/abstract/10.1103/PRXQuantum.2.020321.
https: / / doi.org/ 10.1103 / PRXQuantum.2.020321
[22] TE O'Brien, S. Polla, NC Rubin, WJ Huggins, S. McArdle, S. Boixo, JR McClean und R. Babbush. Fehlerminderung durch verifizierte Phasenschätzung. ArXiv:2010.02538, 2020. 10.1103/PRXQuantum.2.020317. URL https:///arxiv.org/abs/2010.02538.
https: / / doi.org/ 10.1103 / PRXQuantum.2.020317
arXiv: 2010.02538
[23] Alessandro Roggero. Schätzung der spektralen Dichte mit der Gaußschen Integraltransformation. ArXiv:2004.04889, 2020. 10.1103/PhysRevA.102.022409. URL https:///arxiv.org/abs/2004.04889.
https: / / doi.org/ 10.1103 / PhysRevA.102.022409
arXiv: 2004.04889
[24] András Gilyén, Yuan Su, Guang Hao Low und Nathan Wiebe. Quanten-Singulärwert-Transformation und darüber hinaus: Exponentielle Verbesserungen für die Quantenmatrix-Arithmetik. In Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, STOC 2019, Seite 193–204, New York, NY, USA, 2019. Association for Computing Machinery. ISBN 9781450367059. 10.1145/3313276.3316366. URL 10.1145/3313276.3316366.
https: / / doi.org/ 10.1145 / 3313276.3316366
[25] O. Regev. Ein subexponentieller Zeitalgorithmus für das Dihedral-Problem mit versteckten Untergruppen mit Polynomraum. ArXiv:quant-ph/0406151, 2004. 10.48550/arXiv.quant-ph/0406151. URL https:///arxiv.org/abs/quant-ph/0406151.
https:///doi.org/10.48550/arXiv.quant-ph/0406151
arXiv: quant-ph / 0406151
[26] Lin Lin und Yu Tong. Heisenberg-begrenzte Grundzustandsenergieschätzung für frühe fehlertolerante Quantencomputer. ArXiv:2102.11340, 2021. 10.1103/PRXQuantum.3.010318. URL https:///arxiv.org/abs/2102.11340.
https: / / doi.org/ 10.1103 / PRXQuantum.3.010318
arXiv: 2102.11340
[27] Valentin Gebhart, Augusto Smerzi und Luca Pezzè. Heisenberg-begrenzter bayesscher Mehrphasen-Schätzalgorithmus. ArXiv:2010.09075, 2020. 10.1103/PhysRevApplied.16.014035. URL https:///arxiv.org/abs/2010.09075.
https: / / doi.org/ 10.1103 / PhysRevApplied.16.014035
arXiv: 2010.09075
[28] Andrew M. Childs, Yuan Su, Minh C. Tran, Nathan Wiebe und Shuchen Zhu. Theorie des Traberfehlers mit Kommutator-Skalierung. Phys. Rev. X, 11: 011020, Februar 2021. 10.1103/PhysRevX.11.011020. URL https:///link.aps.org/doi/10.1103/PhysRevX.11.011020.
https://doi.org/ 10.1103/PhysRevX.11.011020
[29] Harald Cramer. Mathematische Methoden der Statistik. Princeton University Press, 1946. ISBN 0691080046. 10.1515/9781400883868. URL https:///archive.org/details/in.ernet.dli.2015.223699.
https: / / doi.org/ 10.1515 / 9781400883868
https:///archive.org/details/in.ernet.dli.2015.223699
[30] Calyampudi Radakrishna Rao. Informationen und die erreichbare Genauigkeit bei der Schätzung statistischer Parameter. Stier. Kalkutta Math. Soc., 37: 81–89, 1945. 10.1007/978-1-4612-0919-5_16. URL https:///link.springer.com/chapter/10.1007/978-1-4612-0919-5_16.
https://doi.org/10.1007/978-1-4612-0919-5_16
[31] Yingbo Hua und Tapan Sarkar. Matrix-Pencil-Methode zur Schätzung von Parametern exponentiell gedämpfter/ungedämpfter Sinuskurven im Rauschen. IEEE Transactions on Acoustic Speech and Signal Processing, 38 (5), 1990. 10.1109/29.56027. URL https:///ieeexplore.ieee.org/document/56027.
https: / / doi.org/ 10.1109 / 29.56027
https: / / ieeexplore.ieee.org/ document / 56027
[32] Ankur Moitra. Superauflösung, Extremalfunktionen und die Zustandszahl von Vandermonde-Matrizen. In Proceedings of the Forty-Seventh Annual ACM Symposium on Theory of Computing, STOC '15, Seite 821–830, New York, NY, USA, 2015. Association for Computing Machinery. ISBN 9781450335362. 10.1145/2746539.2746561. URL 10.1145/2746539.2746561.
https: / / doi.org/ 10.1145 / 2746539.2746561
[33] Lin Lin und Yu Tong. Nahezu optimale Grundzustandspräparation. Quantum, 4: 372, Dezember 2020. ISSN 2521-327X. 10.22331/q-2020-12-14-372. URL 10.22331/q-2020-12-14-372.
https://doi.org/10.22331/q-2020-12-14-372
Zitiert von
[1] Casper Gyurik, Chris Cade und Vedran Dunjko, „Auf dem Weg zum Quantenvorteil durch topologische Datenanalyse“, arXiv: 2005.02607.
[2] Kianna Wan, Mario Berta und Earl T. Campbell, „Randomisierter Quantenalgorithmus für statistische Phasenschätzung“, Physische Überprüfungsschreiben 129 3, 030503 (2022).
[3] Andrés Gómez und Javier Mas, „Hermitian Matrix Definiteness from Quantum Phase Estimation“, Quanteninformationsverarbeitung 21 6, 213 (2022).
Die obigen Zitate stammen von SAO / NASA ADS (Zuletzt erfolgreich aktualisiert am 2022, 10:07:02 Uhr). Die Liste ist möglicherweise unvollständig, da nicht alle Verlage geeignete und vollständige Zitationsdaten bereitstellen.
Konnte nicht abrufen Crossref zitiert von Daten während des letzten Versuchs 2022-10-07 02:35:10: Von Crossref konnten keine zitierten Daten für 10.22331 / q-2022-10-06-830 abgerufen werden. Dies ist normal, wenn der DOI kürzlich registriert wurde.
Dieses Papier ist in Quantum unter dem veröffentlicht Creative Commons Namensnennung 4.0 International (CC BY 4.0) Lizenz. Das Copyright verbleibt bei den ursprünglichen Copyright-Inhabern wie den Autoren oder deren Institutionen.