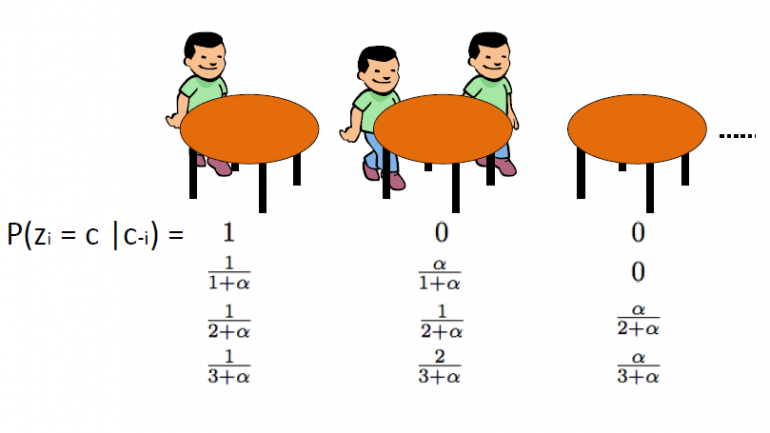Der Dirichlet-Prozess Der chinesische Restaurant-Prozess und andere Darstellungen

• 20. Mai 2014
• Vasilis Vryniotis
• . Keine Kommentare

Dieser Artikel ist der dritte Teil der Reihe zum Clustering mit Dirichlet-Prozessmischungsmodellen. Beim letzten Mal haben wir das Finite-Mixture-Modell basierend auf der Dirichlet-Verteilung definiert und Fragen gestellt, wie wir dieses bestimmte Modell unendlich machen können. Wir haben kurz die Idee diskutiert, die Grenze des Modells zu nehmen, wenn die k-Anzahl von Clustern gegen unendlich tendiert, aber wie wir betont haben, ist die Existenz eines solchen Objekts nicht trivial (mit anderen Worten, wie nehmen wir tatsächlich die Grenze eines Modells? ”?). Zur Erinnerung, der Grund, warum wir k unendlich machen wollen, ist, dass wir auf diese Weise ein nicht parametrisches Modell haben, bei dem wir nicht die Gesamtzahl der Cluster innerhalb der Daten vordefinieren müssen.

Update: Das Datumbox Machine Learning Framework ist jetzt Open Source und kostenlos für herunterladen. Schauen Sie sich das Paket com.datumbox.framework.machinelearning.clustering an, um die Implementierung von Dirichlet Process Mixture Models in Java zu sehen.

Obwohl unser Ziel darin besteht, ein Modell zu erstellen, das Clustering für Datensätze durchführen kann, müssen wir uns zuvor mit Dirichlet-Prozessen befassen. Wir werden sowohl die strengen mathematischen Definitionen als auch die intuitiveren Erklärungen von DP bereitstellen und Möglichkeiten zur Konstruktion des Prozesses diskutieren. Diese Konstruktionen / Darstellungen können als ein Weg gesehen werden, Vorkommen des Dirichlet-Prozesses im „wirklichen Leben“ zu finden.

Trotz der Tatsache, dass ich versucht habe, meinen Forschungsbericht so anzupassen, dass diese Blog-Beiträge leichter zu verfolgen sind, ist es immer noch wichtig, die erforderlichen mathematischen Werkzeuge und Verteilungen zu definieren, bevor wir mit der Verwendung der Modelle beginnen. Dirichlet-Prozessmodelle sind ein Thema aktiver Forschung, erfordern jedoch ein gutes Verständnis der Statistik und der stochastischen Prozesse, bevor sie verwendet werden. Ein weiteres Problem ist, dass Dirichlet-Prozesse, wie wir in diesem Artikel sehen werden, auf zahlreiche Arten dargestellt / konstruiert werden können. Infolgedessen verwenden mehrere wissenschaftliche Arbeiten völlig unterschiedliche Notationen / Konventionen und untersuchen das Problem unter verschiedenen Gesichtspunkten. In diesem Beitrag versuche ich, sie so einfach wie möglich zu erklären und die gleiche Notation zu verwenden. Hoffentlich werden die Dinge mit den beiden kommenden Artikeln klarer, die sich auf die Definition von Dirichlet-Prozessmischungsmodellen und deren tatsächliche Verwendung zur Durchführung von Clusteranalysen konzentrieren.

1. Definition des Dirichlet-Prozesses

Ein Dirichlet-Prozess über einen Θ-Raum ist ein stochastischer Prozess. Es ist eine Wahrscheinlichkeitsverteilung über „Wahrscheinlichkeitsverteilungen über Θ Raum“ und a Daraus ergibt sich eine diskrete Verteilung. Formal ist eine Dirichlet-Verteilung eine Verteilung über Wahrscheinlichkeitsmaße. EIN Wahrscheinlichkeitsmaß ist eine Funktion von Teilmengen des Raumes Θ bis [0,1]. G ist ein DP-verteiltes Zufallswahrscheinlichkeitsmaß, bezeichnet als , wenn für eine Partition (A.₁,…EIN_n) des Raumes Θ wir haben das .

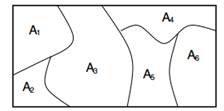
Abbildung 1: Ränder auf endlichen Partitionen sind Dirichlet-verteilt.

Der DP hat zwei Parameter: Der erste ist die Basisverteilung G.₀ das dient wie ein Mittelwert . Der zweite ist der Stärkeparameter α, der streng positiv ist und wie eine inverse Varianz dient . Es bestimmt das Ausmaß der Wiederholung der Werte der Ausgabeverteilung. Je höher der Wert von a ist, desto kleiner ist die Wiederholung; Je kleiner der Wert ist, desto höher ist die Wiederholung der Werte der Ausgabeverteilung. Schließlich ist der Θ-Raum der Parameterraum, auf dem wir den DP definieren. Darüber hinaus ist der Raum Θ auch der Definitionsraum von G.₀ das ist das gleiche wie das von G.

Ein einfacher und mehr intuitive Art und Weise Um einen Dirichlet-Prozess zu erklären, gehen Sie wie folgt vor. Angenommen, wir haben einen Raum Θ, der auf jede endliche Weise partitioniert werden kann (A.₁,…,EIN_n) und eine Wahrscheinlichkeitsverteilung G, die ihnen Wahrscheinlichkeiten zuweist. Das G ist eine spezifische Wahrscheinlichkeitsverteilung über Θ, aber es gibt viele andere. Der Dirichlet-Prozess auf Θ modelliert genau dies; es ist eine Verteilung über alle möglichen Wahrscheinlichkeitsverteilungen im Raum Θ. Der Dirichlet-Prozess wird mit dem G parametriert₀ Basisfunktion und der α-Konzentrationsparameter. Wir können sagen, dass G gemäß DP mit den Parametern α und G verteilt ist₀ wenn die gemeinsame Verteilung der Wahrscheinlichkeiten, die G den Partitionen von Θ zuweist, der Dirichlet-Verteilung folgt. Alternativ können wir sagen, dass die Wahrscheinlichkeiten, die G einer endlichen Partition von Θ zuweist, der Dirichlet-Verteilung folgen.

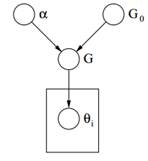
Abbildung 2: Grafisches Modell des Dirichlet-Prozesses

Endlich oben sehen wir die grafisches Modell eines DP. Wir sollten beachten, dass α ein skalarer Hyperparameter G ist₀ ist die Basisverteilung von DP, G eine zufällige Verteilung über den vom DP abgetasteten Θ-Parameterraum, der den Parametern und θ Wahrscheinlichkeiten zuweist_i ist ein Parametervektor, der aus der G-Verteilung gezogen wird und ein Element des Θ-Raums ist.

2. Hintere Dirichlet-Prozesse

Die posterioren Dirichlet-Prozesse wurden von diskutiert Ferguson. Wir beginnen mit dem Zeichnen eines zufälligen Wahrscheinlichkeitsmaßes G aus einem Dirichlet-Prozess. . Da G eine Wahrscheinlichkeitsverteilung über Θ ist, können wir auch aus dieser Verteilung eine Stichprobe ziehen und unabhängige identisch verteilte Stichproben θ zeichnen₁,…, Θ_n ~ G. Da Draws aus einem Dirichlet-Prozess diskrete Verteilungen sind, können wir darstellen woher ist eine kurze Notation für Dies ist eine Delta-Funktion, die 1 if benötigt und 0 anderswo. Ein interessanter Effekt davon ist, dass, da G auf diese Weise definiert ist, eine positive Wahrscheinlichkeit besteht, dass verschiedene Proben den gleichen Wert haben . Wie wir später sehen werden, wird dadurch ein Clustering-Effekt erzeugt, mit dem die Clusteranalyse für Datasets durchgeführt werden kann.

Unter Verwendung der obigen Definitionen und Beobachtungen wollen wir den hinteren Teil des Dirichlet-Prozesses bei gegebenen Proben θ abschätzen. Trotzdem wissen wir das und Durch die Verwendung der Bayes-Regeln und der Konjugation zwischen Dirichlet und Multinomial haben wir das und .

Gleichung 1: Hinterer Dirichlet-Prozess

Diese Eigenschaft ist sehr wichtig und wird von den verschiedenen DP-Darstellungen verwendet.

3. Dirichlet-Prozessdarstellungen

In den vorherigen Segmenten haben wir den Dirichlet-Prozess definiert und sein theoretisches Modell vorgestellt. Eine wichtige Frage, die wir beantworten müssen, ist, woher wir wissen, dass ein solches Objekt existiert und wie wir es können konstruieren und darstellen ein Dirichlet-Prozess.

Die ersten Hinweise auf die Existenz wurden von geliefert Ferguson Wer den Kolmogorov-Konsistenzsatz verwendete, gab die Definition eines Dirichlet-Prozesses an und beschrieb den posterioren Dirichlet-Prozess. Fortsetzung seiner Forschung, Blackwell und MacQueen nutzte den Satz von de Finetti, um die Existenz eines solchen zufälligen Wahrscheinlichkeitsmaßes zu beweisen, und führte das Urnenschema Blackwell-MacQueen ein, das die Eigenschaften des Dirichlet-Prozesses erfüllt. Im Jahr 1994 Seturaman bot eine zusätzliche einfache und direkte Möglichkeit zur Konstruktion eines DP durch Einführung der Stick-Breaking-Konstruktion. Schließlich wurde eine weitere Vertretung von zur Verfügung gestellt Aldous der den chinesischen Restaurantprozess als effektiven Weg zur Konstruktion eines Dirichlet-Prozesses einführte.

Die verschiedenen Darstellungen des Dirichlet-Prozesses sind mathematisch äquivalent, aber ihre Formulierung unterscheidet sich, weil sie das Problem unter verschiedenen Gesichtspunkten untersuchen. Im Folgenden stellen wir die häufigsten Darstellungen in der Literatur vor und konzentrieren uns auf den chinesischen Restaurantprozess, der eine einfache und rechnerisch effiziente Möglichkeit bietet, Inferenzalgorithmen für den Dirichlet-Prozess zu erstellen.

3.1 Das Urnenschema Blackwell-MacQueen

Das Urnenschema Blackwell-MacQueen kann zur Darstellung eines Dirichlet-Prozesses verwendet werden und wurde von eingeführt Blackwell und MacQueen. Es basiert auf dem Urnenschema von Pólya, das als das entgegengesetzte Modell der ersatzlosen Probenahme angesehen werden kann. Im Urnenschema von Pólya nehmen wir an, dass wir eine nicht transparente Urne haben, die farbige Kugeln enthält, und wir ziehen Kugeln zufällig. Wenn wir einen Ball zeichnen, beobachten wir seine Farbe, legen ihn wieder in die Urne und fügen einen zusätzlichen Ball derselben Farbe hinzu. Ein ähnliches Schema wird von Blackwell und MacQueen verwendet, um einen Dirichlet-Prozess zu konstruieren.

Dieses Schema erzeugt eine Folge von θ₁, θ₂,… Mit bedingte Wahrscheinlichkeiten . In diesem Schema nehmen wir an, dass G.₀ ist eine Verteilung über Farben und jedes θ_n repräsentiert die Farbe der Kugel, die in die Urne gelegt wird. Das Algorithmus ist wie folgt:

· Wir beginnen mit einer leeren Urne.

· Mit einer Wahrscheinlichkeit proportional zu α wir zeichnen und wir fügen einen Ball dieser Farbe in die Urne.

· Mit einer Wahrscheinlichkeit proportional zu n-1 ziehen wir eine zufällige Kugel aus der Urne, beobachten ihre Farbe, legen sie zurück in die Urne und fügen der Urne eine zusätzliche Kugel derselben Farbe hinzu.

Zuvor haben wir mit einem Dirichlet-Prozess begonnen und das Blackwell-MacQueen-Schema abgeleitet. Beginnen wir nun umgekehrt mit dem Blackwell-MacQueen-Schema und leiten den DP ab. Da θ_i Wurden in einer bestimmten Weise aus G gezogen, ist ihre gemeinsame Verteilung für alle endlichen Permutationen unveränderlich und somit austauschbar. Wenn wir also den Satz von de Finetti verwenden, müssen wir eine Verteilung über die Maße haben, um sie iid zu machen, und diese Verteilung ist der Dirichlet-Prozess. Als Ergebnis beweisen wir, dass das Urnenschema von Blackwell-MacQueen eine Darstellung von DP ist und uns einen konkreten Weg gibt, es zu konstruieren. Wie wir später sehen werden, entspricht dieses Schema mathematisch dem chinesischen Restaurantprozess.

3.2 Die Stick-Breaking-Konstruktion

Die Stick-Breaking-Konstruktion ist eine alternative Möglichkeit, einen Dirichlet-Prozess darzustellen, der von eingeführt wurde Seturaman. Es ist eine konstruktive Art, die Verteilung und verwendet die folgende Analogie: Wir nehmen an, dass wir einen Stock der Länge 1 haben, wir brechen ihn an Position β₁ und wir weisen π zu₁ gleich der Länge des Teils des Stocks, den wir gebrochen haben. Wir wiederholen den gleichen Vorgang, um π zu erhalten₂, p₃,… etc; Aufgrund der Art und Weise, wie dieses Schema definiert ist, können wir es unendlich oft fortsetzen.

Basierend auf dem oben genannten π_k kann modelliert werden als , Wobei die während wie in den vorherigen Schemata die θ direkt von der Basisverteilung abgetastet werden . Folglich kann die G-Verteilung als eine Summe von mit π gewichteten Delta-Funktionen geschrieben werden_k Wahrscheinlichkeiten, die gleich sind . Die Stick-Breaking-Konstruktion bietet uns somit eine einfache und intuitive Möglichkeit, einen Dirichlet-Prozess zu konstruieren.

3.3 Der chinesische Restaurantprozess

Der chinesische Restaurantprozess, der von eingeführt wurde Aldousist eine weitere effektive Methode zur Darstellung eines Dirichlet-Prozesses und kann direkt mit dem Urnenschema Blackwell-MacQueen verknüpft werden. Dieses Schema verwendet die folgende Analogie: Wir gehen davon aus, dass es ein chinesisches Restaurant mit unendlich vielen Tischen gibt. Wenn die Kunden das Restaurant betreten, sitzen sie zufällig an einem der besetzten Tische oder setzen sich an den ersten verfügbaren leeren Tisch.

Das CRP definiert eine Verteilung auf den Raum der Partitionen der positiven ganzen Zahlen. Wir beginnen mit dem Zeichnen von θ₁,… Θ_n aus dem Urnenschema von Blackwell-MacQueen. Wie wir in den vorherigen Segmenten besprochen haben, erwarten wir einen Clustering-Effekt und daher wird die Gesamtzahl der eindeutigen θ-Werte k signifikant kleiner als n sein. Dies definiert also eine Partition der Menge {1,2,…, n} in k Clustern. Folglich induziert das Zeichnen aus dem Urnenschema von Blackwell-MacQueen eine zufällige Partition der Menge {1,2,…, n}. Der chinesische Restaurantprozess wird dadurch induziert Verteilung über Partitionen. Der Algorithmus ist wie folgt:

· Wir beginnen mit einem leeren Restaurant.

· Die 1^st Kunde sitzt immer auf 1^st Tabelle

· Das n + 1^th Kunde hat 2 Möglichkeiten:

o Setzen Sie sich mit Wahrscheinlichkeit auf den ersten unbesetzten Tisch

o Setzen Sie sich mit Wahrscheinlichkeit auf einen der k-ten besetzten Tische
woher ist die Anzahl der Personen, die auf diesem Tisch sitzen

Dabei ist α der Dispersionswert von DP und n die Gesamtzahl der Kunden im Restaurant zu einem bestimmten Zeitpunkt. Die latente Variable z_i speichert die Tabellennummer des i^th Kunde und nimmt Werte von 1 bis k_n wo k_n ist die Gesamtzahl der belegten Tische, wenn n Kunden im Restaurant sind. Wir sollten beachten, dass die k_n wird immer kleiner oder gleich n sein und im Durchschnitt geht es um . Schließlich sollten wir beachten, dass die Wahrscheinlichkeit der Tabellenanordnung ist gegenüber Permutationen unveränderlich. So ist die z_i ist austauschbar, was bedeutet, dass Tabellen mit der gleichen Kundengröße die gleiche Wahrscheinlichkeit haben.

Der chinesische Restaurantprozess ist eng mit dem Urnenschema von Pólya und dem Dirichlet-Prozess verbunden. Das CRP ist eine Möglichkeit, a anzugeben Verteilung über Partitionen (Tabellenzuordnungen) von n Punkten und kann als Prior auf dem Raum der latenten Variablen z verwendet werden_i welche bestimmt die Clusterzuordnungen. Das CRP entspricht dem Urnenschema von Pólya, mit dem Unterschied, dass nicht jeder Tabelle / jedem Cluster Parameter zugewiesen werden. Gehen von CRP zu Pólyas Urnenschema wir zeichnen für alle Tabellen k = 1,2… und dann für jedes x_i welches in Tabelle z gruppiert ist_i zuweisen a . Mit anderen Worten, ordnen Sie das neue x zu_i der Parameter θ der Tabelle. Endlich da wir können nicht zuweisen Wenn θ von Anfang an unendlich ist, können wir jedes Mal, wenn jemand auf einem neuen Tisch sitzt, ein neues θ zuweisen. Aus all diesen Gründen kann uns das CRP dabei helfen, rechnerisch effiziente Algorithmen zur Durchführung der Clusteranalyse für Datensätze zu erstellen.

In diesem Beitrag haben wir den Dirichlet-Prozess und verschiedene Möglichkeiten zu seiner Konstruktion besprochen. Wir werden die obigen Ideen im nächsten Artikel verwenden. Wir werden das Dirichlet-Prozessmischungsmodell einführen und die chinesische Restaurantdarstellung verwenden, um den Dirichlet-Prozess zu konstruieren und die Clusteranalyse durchzuführen. Wenn Sie einige Punkte verpasst haben, machen Sie sich keine Sorgen, da die Dinge mit den nächsten beiden Artikeln klarer werden.

Ich hoffe, Sie fanden diesen Beitrag interessant. Wenn Sie dies getan haben, nehmen Sie sich einen Moment Zeit, um es auf Facebook und Twitter zu teilen. 🙂