Das Eichbild der Quantendynamik

Das Eichbild der Quantendynamik

Zeitstempel: 21. März 2024, 6:43 Uhr

Kevin Slagle

Fakultät für Elektrotechnik und Informationstechnik, Rice University, Houston, Texas 77005 USA
Fakultät für Physik, California Institute of Technology, Pasadena, Kalifornien 91125, USA
Institut für Quanteninformation und Materie und Walter Burke Institut für Theoretische Physik, California Institute of Technology, Pasadena, Kalifornien 91125, USA

Findest du dieses Paper interessant oder möchtest du darüber diskutieren? Scite oder hinterlasse einen Kommentar zu SciRate.

Abstrakt

Obwohl lokale Hamiltonoperatoren eine lokale Zeitdynamik aufweisen, ist diese Lokalität im Schrödinger-Bild nicht explizit in dem Sinne, dass die Wellenfunktionsamplituden keiner lokalen Bewegungsgleichung gehorchen. Wir zeigen, dass geometrische Lokalität explizit in den Bewegungsgleichungen erreicht werden kann, indem die globale einheitliche Invarianz der Quantenmechanik in eine lokale Eichinvarianz „gemessen“ wird. Das heißt, die Erwartungswerte $langle psi|A|psi rangle$ sind invariant unter einer globalen einheitlichen Transformation, die auf die Wellenfunktion $|psirangle zu U |psirangle$ und die Operatoren $A zu UAU^dagger$ wirkt, und wir zeigen, dass dies möglich ist diese globale Invarianz in eine lokale Eichinvarianz umzuwandeln. Dazu ersetzen wir die Wellenfunktion durch eine Sammlung lokaler Wellenfunktionen $|psi_Jrangle$, eine für jedes Raumstück $J$. Die Sammlung räumlicher Patches wird so gewählt, dass sie den Raum abdeckt; Beispielsweise könnten wir die Patches als einzelne Qubits oder als Standorte mit den nächsten Nachbarn auf einem Gitter auswählen. Lokale Wellenfunktionen, die benachbarten Paaren räumlicher Patches $I$ und $J$ zugeordnet sind, stehen durch dynamische einheitliche Transformationen $U_{IJ}$ miteinander in Beziehung. Die lokalen Wellenfunktionen sind lokal in dem Sinne, dass ihre Dynamik lokal ist. Das heißt, die Bewegungsgleichungen für die lokalen Wellenfunktionen $|psi_Jrangle$ und Verbindungen $U_{IJ}$ sind explizit lokal im Raum und hängen nur von benachbarten Hamilton-Termen ab. (Die lokalen Wellenfunktionen sind Vielteilchenwellenfunktionen und haben die gleiche Hilbertraumdimension wie die übliche Wellenfunktion.) Wir nennen dieses Bild der Quantendynamik das Eichbild, da es eine lokale Eichinvarianz aufweist. Die lokale Dynamik eines einzelnen räumlichen Patches hängt mit dem Interaktionsbild zusammen, wobei der Hamilton-Interaktionsoperator nur aus benachbarten Hamiltonian-Termen besteht. Wir können die explizite Lokalität auch so verallgemeinern, dass sie die Lokalität in lokale Ladungs- und Energiedichten einbezieht.

Das Messgerätebild von Quantum Dynamics PlatoBlockchain Data Intelligence. Vertikale Suche. Ai.

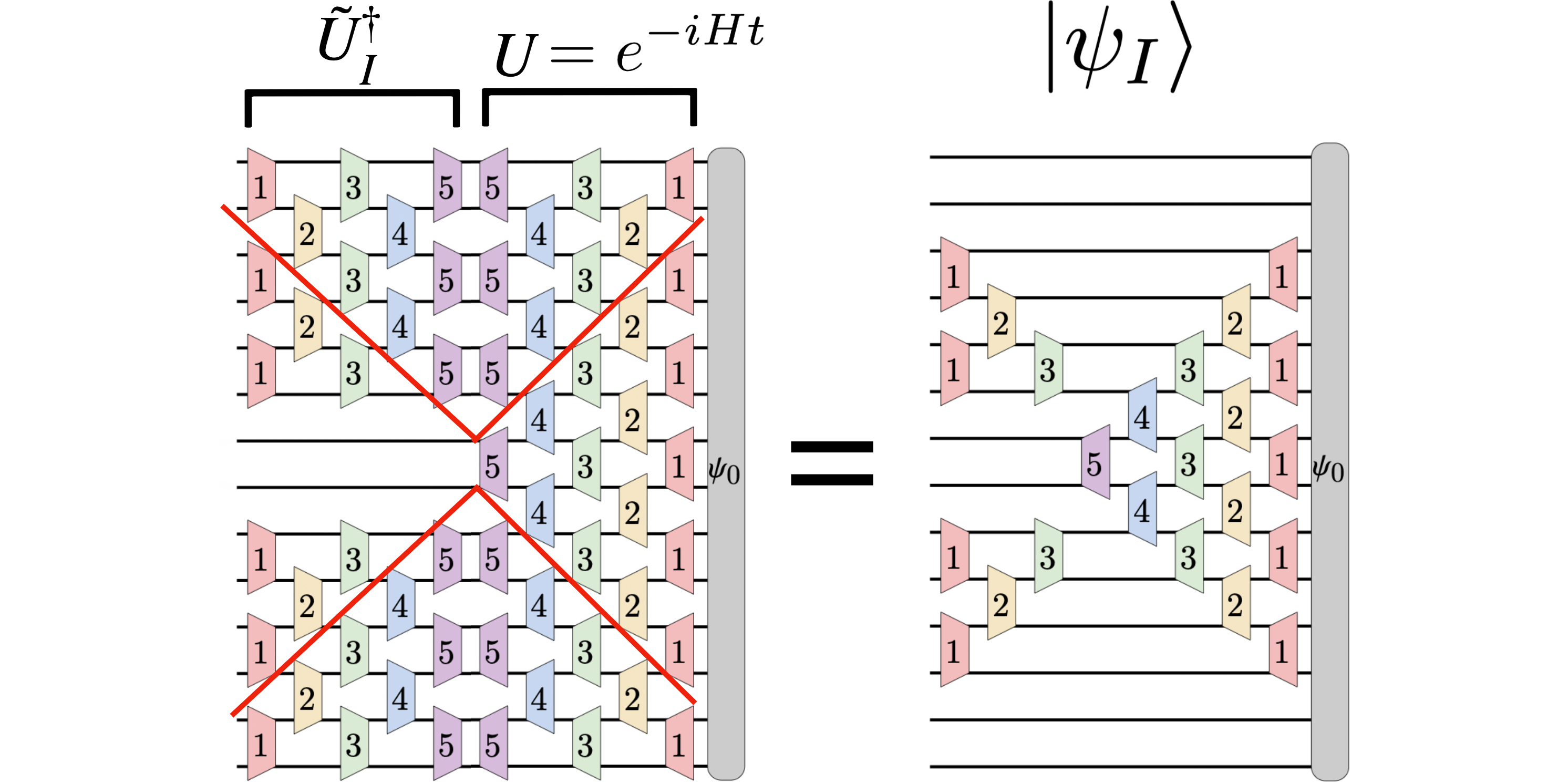
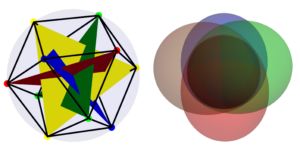
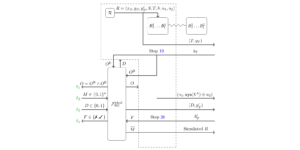
Ausgewähltes Bild: In Schrödingers Bild entwickelt sich eine anfängliche Wellenfunktion $|psi_0rangle$ nach einer Zeit $t$ zu $U(t) |psi_0rangle$, wobei $U(t) = e^{-iHt}$ die einheitliche Zeitentwicklung ist Operator. Das Messgerätbild berücksichtigt stattdessen lokale Wellenfunktionen $|psi_I(t)rangle$, die einer Teilmenge (oder einem Patch) $I$ im Raum zugeordnet sind. Die zeitlich entwickelte lokale Wellenfunktion $|psi_I(t)rangle = tilde{U}_I^dagger(t) |psi(t)rangle$ wird aus Schrödingers Wellenfunktion $|psi(t)rangle = U(t) |psi_0rangle erhalten $ über den einheitlichen Operator $tilde{U}_I^dagger(t)$, der die Zeitentwicklung außerhalb der Region $I$ umkehrt. Infolgedessen hängt die Dynamik der lokalen Wellenfunktion $partial_I |psi_I(t)rangle$ nur von benachbarten Hamilton-Termen ab, die sich mit der Region $I$ überlappen. Die Abbildung stellt diese einheitlichen Operatoren als Quantenschaltkreise dar und zeigt, dass sich die Zeitentwicklung von $U(t)$ größtenteils durch $tilde{U}_I^dagger(t)$ aufhebt und nur ein sanduhrförmiger Zeitentwicklungsoperator übrig bleibt Wirkt auf die anfängliche Wellenfunktion (rechts in der Abbildung). Dieser sanduhrförmige Operator ist analog zum lichtkegelförmigen Operatorwachstum in Heisenbergs Bild.

Populäre Zusammenfassung

Die beiden bekanntesten Bilder der Quantendynamik sind das Schrödinger- und das Heisenberg-Bild. In Schrödingers Bild entwickelt sich die Wellenfunktion mit der Zeit, während in Heisenbergs Bild die Wellenfunktion konstant ist, aber die Operatoren sich mit der Zeit entwickeln. In dieser Arbeit stellen wir ein neues Bild der Quantendynamik vor, das Eichbild, das tiefe Verbindungen zur Lokalität von Informationen und zur Eichtheorie herstellt.

Zur Lokalität: Ein schöner Vorteil von Heisenbergs Bild ist, dass die Lokalität in den Bewegungsgleichungen explizit ist. Das heißt, die zeitliche Entwicklung eines lokalen Betreibers hängt nur vom Zustand nahegelegener lokaler Betreiber ab. Im Gegensatz dazu ist die Lokalität in Schrödingers Bild nicht auf diese Weise explizit, für das es eine einzige Wellenfunktion gibt, deren Zeitdynamik überall im Raum von Operatoren abhängt. Unser neues Eichbild modifiziert Schrödingers Bild so, dass wir eine „lokale Wellenfunktion“ berechnen können, die die gleichen Informationen wie Schrödingers Wellenfunktion enthält. Es ist zu erwarten, dass die Zeitdynamik lokaler Wellenfunktionen im Eichbild nur von benachbarten Hamilton-Termen abhängt, was die Lokalität explizit macht Bewegungsgleichungen. Um diese explizite Lokalität zu erreichen, fügt das Eichbild den Bewegungsgleichungen Eichfelder hinzu.

Die Eichtheorie stellt eine tiefe Verbindung zwischen einem Hamilton-Operator (oder Lagrange-Operator) mit globaler Symmetrie und einem anderen Hamilton-Operator her, bei dem die globale Symmetrie über die zusätzlichen dynamischen Eichfelder durch eine lokale Eichsymmetrie ersetzt wird. Interessanterweise lässt Schrödingers Gleichung $ihbar partielle_t |psirangle = H |psirangle$ eine globale einheitliche Invarianz zu, die durch die Transformation von $|psirangle zu U |psirangle$ und $H zu UHU^dagger$ gegeben ist. Unsere Arbeit zeigt, dass es auch möglich ist, die Eichtheorie auf diese globale Invarianz in der Schrödinger-Gleichung anzuwenden, um eine neue Bewegungsgleichung, nämlich das Eichbild, mit dynamischen Eichfeldern und einer lokalen Eichinvarianz zu erhalten.

► BibTeX-Daten

► Referenzen

[1] David Deutsch und Patrick Hayden. „Informationsfluss in verschränkten Quantensystemen“. Proceedings of the Royal Society of London Series A 456, 1759 (2000). arXiv:quant-ph/​9906007.
https: / / doi.org/ 10.1098 / rspa.2000.0585
arXiv: quant-ph / 9906007

[2] Michael A. Levin und Xiao-Gang Wen. „String-Net-Kondensation: Ein physikalischer Mechanismus für topologische Phasen“. Physik. Rev. B 71, 045110 (2005). arXiv:cond-mat/​0404617.
https://doi.org/ 10.1103/PhysRevB.71.045110
arXiv: cond-mat / 0404617

[3] T. Senthil, Ashvin Vishwanath, Leon Balents, Subir Sachdev und Matthew PA Fisher. „Dekonfinierte quantenkritische Punkte“. Wissenschaft 303, 1490–1494 (2004). arXiv:cond-mat/​0311326.
https: / / doi.org/ 10.1126 / science.1091806
arXiv: cond-mat / 0311326

[4] Beni Yoshida. „Exotische topologische Ordnung in fraktalen Spinflüssigkeiten“. Physik. Rev. B 88, 125122 (2013). arXiv:1302.6248.
https://doi.org/ 10.1103/PhysRevB.88.125122
arXiv: 1302.6248

[5] Kevin Hartnett. „Matrixmultiplikation kommt dem mythischen Ziel nur wenige Zentimeter näher“. Quanta Magazin (2021). URL: https://www.quantamagazine.org/​mathematicians-inch-closer-to-matrix-multiplication-goal-20210323/​.
https://www.quantamagazine.org/​mathematicians-inch-closer-to-matrix-multiplication-goal-20210323/​

[6] Volker Straßen. „Gaußsche Eliminierung ist nicht optimal“. Numerische Mathematik 13, 354–356 (1969).
https: / / doi.org/ 10.1007 / BF02165411

[7] Kevin Slagle. „Quantenmessnetzwerke: Eine neue Art von Tensornetzwerk“. Quantum 7, 1113 (2023). arXiv:2210.12151.
https:/​/​doi.org/​10.22331/​q-2023-09-14-1113
arXiv: 2210.12151

[8] Román Orús. „Eine praktische Einführung in Tensornetzwerke: Matrixproduktzustände und projizierte verschränkte Paarzustände“. Annals of Physics 349, 117–158 (2014). arXiv:1306.2164.
https: / / doi.org/ 10.1016 / j.aop.2014.06.013
arXiv: 1306.2164

[9] Michael P. Zaletel und Frank Pollmann. „Isometrische Tensornetzwerkzustände in zwei Dimensionen“. Physik. Rev. Lett. 124, 037201 (2020). arXiv:1902.05100.
https://doi.org/ 10.1103/PhysRevLett.124.037201
arXiv: 1902.05100

[10] Steven Weinberg. „Testen der Quantenmechanik“. Annals of Physics 194, 336–386 (1989).
https:/​/​doi.org/​10.1016/​0003-4916(89)90276-5

[11] N. Gisin. „Weinbergs nichtlineare Quantenmechanik und supraluminale Kommunikation“. Physikbriefe A 143, 1–2 (1990).
https:/​/​doi.org/​10.1016/​0375-9601(90)90786-N

[12] Joseph Polchinski. „Weinbergs nichtlineare Quantenmechanik und das Einstein-Podolsky-Rosen-Paradoxon“. Physik. Rev. Lett. 66, 397–400 (1991).
https://doi.org/ 10.1103/PhysRevLett.66.397

[13] Kevin Slagle. „Testen der Quantenmechanik mit lauten Quantencomputern“ (2021). arXiv:2108.02201.
arXiv: 2108.02201

[14] Brian Swingle. „Entschlüsselung der Physik von Korrelatoren außerhalb der zeitlichen Ordnung“. Nature Physics 14, 988–990 (2018).
https:/​/​doi.org/​10.1038/​s41567-018-0295-5

[15] Ignacio García-Mata, Rodolfo A. Jalabert und Diego A. Wisniacki. „Korrelatoren außerhalb der zeitlichen Ordnung und Quantenchaos“ (2022). arXiv:2209.07965.
arXiv: 2209.07965

[16] Rahul Nandkishore und David A. Huse. „Vielteilchenlokalisierung und Thermalisierung in der quantenstatistischen Mechanik“. Jahresrückblick auf die Physik der kondensierten Materie 6, 15–38 (2015). arXiv:1404.0686.
https: // doi.org/ 10.1146 / annurev-conmatphys-031214-014726
arXiv: 1404.0686

[17] Dmitry A. Abanin, Ehud Altman, Immanuel Bloch und Maksym Serbyn. „Kolloquium: Vielkörperlokalisierung, Thermalisierung und Verschränkung“. Rezensionen von Modern Physics 91, 021001 (2019). arXiv:1804.11065.
https: / / doi.org/ 10.1103 / RevModPhys.91.021001
arXiv: 1804.11065

[18] Bruno Nachtergaele und Robert Sims. „Viel Lärm um etwas: Warum Lieb-Robinson-Grenzen nützlich sind“ (2011). arXiv:1102.0835.
arXiv: 1102.0835

[19] Daniel A. Roberts und Brian Swingle. „Lieb-Robinson-Grenze und der Schmetterlingseffekt in Quantenfeldtheorien“. Physik. Rev. Lett. 117, 091602 (2016). arXiv:1603.09298.
https://doi.org/ 10.1103/PhysRevLett.117.091602
arXiv: 1603.09298

[20] Zhiyuan Wang und Kaden RA Hazzard. „Verschärfung der Lieb-Robinson-Bindung in lokal interagierenden Systemen“. PRX Quantum 1, 010303 (2020). arXiv:1908.03997.
https: / / doi.org/ 10.1103 / PRXQuantum.1.010303
arXiv: 1908.03997

Zitiert von

[1] Sayak Guha Roy und Kevin Slagle, „Interpolation zwischen der Eich- und Schrödinger-Bildern der Quantendynamik“, SciPost Physics Core 6 4, 081 (2023).

[2] Kevin Slagle, „Quantum Gauge Networks: Eine neue Art von Tensor-Netzwerk“, Quantum 7, 1113 (2023).

Die obigen Zitate stammen von SAO / NASA ADS (Zuletzt erfolgreich aktualisiert am 2024, 03:22:22 Uhr). Die Liste ist möglicherweise unvollständig, da nicht alle Verlage geeignete und vollständige Zitationsdaten bereitstellen.

On Der von Crossref zitierte Dienst Es wurden keine Daten zum Zitieren von Werken gefunden (letzter Versuch 2024-03-22 22:55:38).

Dieses Papier ist in Quantum unter dem veröffentlicht Creative Commons Namensnennung 4.0 International (CC BY 4.0) Lizenz. Das Copyright verbleibt bei den ursprünglichen Copyright-Inhabern wie den Autoren oder deren Institutionen.

Zeitstempel:

Mehr von Quantenjournal