Σημειώσεις Big O και Ανάλυση Αλγορίθμων με Παραδείγματα Python

Εισαγωγή

Υπάρχουν συνήθως πολλοί τρόποι επίλυσης του προβλήματος χρησιμοποιώντας ένα πρόγραμμα υπολογιστή. Για παράδειγμα, υπάρχουν διάφοροι τρόποι ταξινόμησης στοιχείων σε έναν πίνακα – μπορείτε να χρησιμοποιήσετε συγχώνευση είδος, τύπος φυσαλίδων, είδος εισαγωγής, και ούτω καθεξής. Όλοι αυτοί οι αλγόριθμοι έχουν τα δικά τους πλεονεκτήματα και μειονεκτήματα και η δουλειά του προγραμματιστή είναι να τους σταθμίσει για να μπορεί να επιλέξει τον καλύτερο αλγόριθμο που θα χρησιμοποιηθεί σε κάθε περίπτωση χρήσης. Με άλλα λόγια, το κύριο ερώτημα είναι ποιος αλγόριθμος να χρησιμοποιήσει για να λύσει ένα συγκεκριμένο πρόβλημα όταν υπάρχουν πολλαπλές λύσεις στο πρόβλημα.

Ανάλυση αλγορίθμων αναφέρεται στην ανάλυση της πολυπλοκότητας διαφορετικών αλγορίθμων και στην εύρεση του πιο αποτελεσματικού αλγορίθμου για την επίλυση του προβλήματος. Σημείωση Big-O είναι ένα στατιστικό μέτρο που χρησιμοποιείται για να περιγράψει την πολυπλοκότητα του αλγορίθμου.

Σε αυτόν τον οδηγό, θα κάνουμε πρώτα μια σύντομη ανασκόπηση της ανάλυσης αλγορίθμων και στη συνέχεια θα ρίξουμε μια πιο βαθιά ματιά στη σημειογραφία Big-O. Θα δούμε πώς μπορεί να χρησιμοποιηθεί η σημείωση Big-O για την εύρεση της πολυπλοκότητας του αλγορίθμου με τη βοήθεια διαφορετικών συναρτήσεων Python.

Γιατί είναι σημαντική η ανάλυση αλγορίθμων;

Για να κατανοήσουμε γιατί η ανάλυση αλγορίθμων είναι σημαντική, θα λάβουμε τη βοήθεια ενός απλού παραδείγματος. Ας υποθέσουμε ότι ένας διευθυντής δίνει μια εργασία σε δύο από τους υπαλλήλους του να σχεδιάσουν έναν αλγόριθμο στην Python που υπολογίζει το παραγοντικό ενός αριθμού που έχει εισαχθεί από τον χρήστη. Ο αλγόριθμος που αναπτύχθηκε από τον πρώτο υπάλληλο μοιάζει με αυτό:

def fact(n):
    product = 1
    for i in range(n):
        product = product * (i+1)
    return product

print(fact(5))

Παρατηρήστε ότι ο αλγόριθμος παίρνει απλώς έναν ακέραιο ως όρισμα. μεσα στην fact() συνάρτηση μιας μεταβλητής με όνομα product αρχικοποιείται σε 1. Ένας βρόχος εκτελείται από 1 προς την n και κατά τη διάρκεια κάθε επανάληψης, η τιμή στο product πολλαπλασιάζεται με τον αριθμό που επαναλαμβάνεται από τον βρόχο και το αποτέλεσμα αποθηκεύεται στο product μεταβλητή ξανά. Μετά την εκτέλεση του βρόχου, το product η μεταβλητή θα περιέχει το παραγοντικό.

Ομοίως, ο δεύτερος υπάλληλος ανέπτυξε επίσης έναν αλγόριθμο που υπολογίζει το παραγοντικό ενός αριθμού. Ο δεύτερος υπάλληλος χρησιμοποίησε μια αναδρομική συνάρτηση για να υπολογίσει το παραγοντικό του αριθμού n:

def fact2(n):
    if n == 0:
        return 1
    else:
        return n * fact2(n-1)

print(fact2(5))

Ο διαχειριστής πρέπει να αποφασίσει ποιον αλγόριθμο θα χρησιμοποιήσει. Για να γίνει αυτό, αποφάσισαν να επιλέξουν ποιος αλγόριθμος τρέχει πιο γρήγορα. Ένας τρόπος για να το κάνετε αυτό είναι να βρείτε τον χρόνο που απαιτείται για την εκτέλεση του κώδικα στην ίδια είσοδο.

Στο σημειωματάριο Jupyter, μπορείτε να χρησιμοποιήσετε το %timeit κυριολεκτική ακολουθούμενη από την κλήση συνάρτησης για να βρεθεί ο χρόνος που χρειάζεται η συνάρτηση για να εκτελεστεί:

%timeit fact(50)

Αυτό θα μας δώσει:

9 µs ± 405 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Η έξοδος λέει ότι ο αλγόριθμος παίρνει 9 μικροδευτερόλεπτα (συν/πλην 45 νανοδευτερόλεπτα) ανά βρόχο.

Ομοίως, μπορούμε να υπολογίσουμε πόσο χρόνο χρειάζεται για να εκτελεστεί η δεύτερη προσέγγιση:

%timeit fact2(50)

Αυτό θα έχει ως αποτέλεσμα:

15.7 µs ± 427 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Ο δεύτερος αλγόριθμος που περιλαμβάνει την αναδρομή παίρνει 15 μικροδευτερόλεπτα (συν/πλην 427 νανοδευτερόλεπτα).

Ο χρόνος εκτέλεσης δείχνει ότι ο πρώτος αλγόριθμος είναι ταχύτερος σε σύγκριση με τον δεύτερο αλγόριθμο που περιλαμβάνει αναδρομή. Όταν πρόκειται για μεγάλες εισροές, η διαφορά απόδοσης μπορεί να γίνει πιο σημαντική.

Ωστόσο, ο χρόνος εκτέλεσης δεν είναι μια καλή μέτρηση για τη μέτρηση της πολυπλοκότητας ενός αλγορίθμου, καθώς εξαρτάται από το υλικό. Απαιτείται μια πιο αντικειμενική μέτρηση ανάλυσης πολυπλοκότητας για έναν αλγόριθμο. Εδώ είναι που το Σημείωση Big O έρχεται να παίξει.

Ανάλυση Αλγορίθμων με Σημείωση Big-O

Ο συμβολισμός Big-O υποδηλώνει τη σχέση μεταξύ της εισόδου στον αλγόριθμο και των βημάτων που απαιτούνται για την εκτέλεση του αλγόριθμου. Συμβολίζεται με ένα μεγάλο «Ο» ακολουθούμενο από μια παρένθεση ανοίγματος και κλεισίματος. Μέσα στην παρένθεση, η σχέση μεταξύ της εισόδου και των βημάτων που κάνει ο αλγόριθμος παρουσιάζεται χρησιμοποιώντας το «n».

Η βασική λύση είναι - ο Big-O δεν ενδιαφέρεται για α Ειδικότερα περίπτωση κατά την οποία εκτελείτε έναν αλγόριθμο, όπως π.χ fact(50), αλλά μάλλον πόσο καλά το κάνει κλίμακα δεδομένης αυξανόμενης εισροής. Αυτή είναι μια πολύ καλύτερη μέτρηση για την αξιολόγηση από τον συγκεκριμένο χρόνο για μια συγκεκριμένη περίπτωση!

Για παράδειγμα, εάν υπάρχει α γραμμική σχέση μεταξύ της εισόδου και του βήματος που κάνει ο αλγόριθμος για την ολοκλήρωση της εκτέλεσής του, η σημείωση Big-O που χρησιμοποιείται θα είναι O (n). Ομοίως, η σημείωση Big-O για τετραγωνικές συναρτήσεις is O(n²).

Για να χτίσετε τη διαίσθηση:

• O (n): στο n=1, γίνεται 1 βήμα. Στο n=10, γίνονται 10 βήματα.
• O(n²): στο n=1, γίνεται 1 βήμα. Στο n=10, γίνονται 100 βήματα.

At n=1, αυτοί οι δύο θα έκαναν το ίδιο! Αυτός είναι ένας άλλος λόγος για τον οποίο η παρατήρηση της σχέσης μεταξύ της εισόδου και του αριθμού των βημάτων για την επεξεργασία αυτής της εισόδου είναι καλύτερη από την απλή αξιολόγηση συναρτήσεων με κάποια συγκεκριμένη είσοδο.

Οι παρακάτω είναι μερικές από τις πιο κοινές λειτουργίες Big-O:

Όνομα	Μεγάλη Ο
συνεχής	Ο (γ)
Γραμμικός	O (n)
Τετραγωνικός	O(n²)
κυβικά	O(n³)
Εκθετικός	O(2ⁿ)
Λογαριθμική	O (ημερολόγιο (n))
Γραμμικό αρχείο καταγραφής	O(nlog(n))

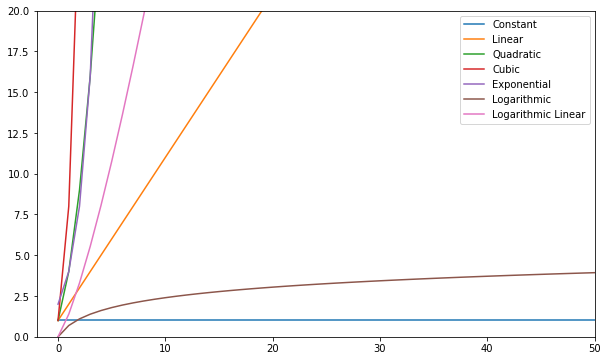
Μπορείτε να απεικονίσετε αυτές τις λειτουργίες και να τις συγκρίνετε:

Σε γενικές γραμμές – οτιδήποτε χειρότερο από το γραμμικό θεωρείται κακή πολυπλοκότητα (δηλαδή αναποτελεσματικό) και θα πρέπει να αποφεύγεται αν είναι δυνατόν. Η γραμμική πολυπλοκότητα είναι εντάξει και συνήθως είναι αναγκαίο κακό. Η λογαριθμική είναι καλή. Το Constant είναι καταπληκτικό!

Για να έχουμε μια ιδέα για το πώς υπολογίζεται ένα Big-O, ας ρίξουμε μια ματιά σε μερικά παραδείγματα σταθερής, γραμμικής και τετραγωνικής πολυπλοκότητας.

Σταθερή πολυπλοκότητα - O(C)

Η πολυπλοκότητα ενός αλγορίθμου λέγεται ότι είναι σταθερή εάν τα βήματα που απαιτούνται για την ολοκλήρωση της εκτέλεσης ενός αλγορίθμου παραμένουν σταθερά, ανεξάρτητα από τον αριθμό των εισόδων. Η σταθερή πολυπλοκότητα συμβολίζεται με Ο (γ) όπου c μπορεί να είναι οποιοσδήποτε σταθερός αριθμός.

Ας γράψουμε έναν απλό αλγόριθμο στην Python που βρίσκει το τετράγωνο του πρώτου στοιχείου στη λίστα και μετά το εκτυπώνει στην οθόνη:

def constant_algo(items):
    result = items[0] * items[0]
    print(result)

constant_algo([4, 5, 6, 8])

Στο παραπάνω σενάριο, ανεξάρτητα από το μέγεθος εισόδου, ή τον αριθμό των στοιχείων στη λίστα εισαγωγής items, ο αλγόριθμος εκτελεί μόνο 2 βήματα:

1. Εύρεση του τετραγώνου του πρώτου στοιχείου
2. Εκτύπωση του αποτελέσματος στην οθόνη.

Ως εκ τούτου, η πολυπλοκότητα παραμένει σταθερή.

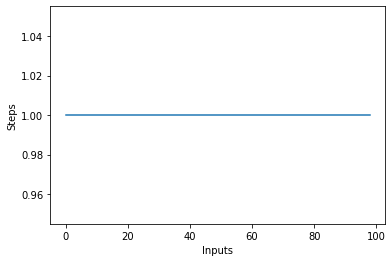
Εάν σχεδιάσετε μια γραμμική γραφική παράσταση με το ποικίλο μέγεθος του items εισαγωγή στον άξονα Χ και τον αριθμό των βημάτων στον άξονα Υ, θα έχετε μια ευθεία γραμμή. Ας δημιουργήσουμε ένα σύντομο σενάριο για να μας βοηθήσει να το οπτικοποιήσουμε αυτό. Ανεξάρτητα από τον αριθμό των εισόδων, ο αριθμός των βημάτων που εκτελούνται παραμένει ο ίδιος:

steps = []
def constant(n):
    return 1
    
for i in range(1, 100):
    steps.append(constant(i))
plt.plot(steps)

Γραμμική πολυπλοκότητα - O (n)

Η πολυπλοκότητα ενός αλγορίθμου λέγεται ότι είναι γραμμική εάν τα βήματα που απαιτούνται για την ολοκλήρωση της εκτέλεσης ενός αλγορίθμου αυξάνονται ή μειώνονται γραμμικά με τον αριθμό των εισόδων. Η γραμμική πολυπλοκότητα συμβολίζεται με O (n).

Σε αυτό το παράδειγμα, ας γράψουμε ένα απλό πρόγραμμα που εμφανίζει όλα τα στοιχεία της λίστας στην κονσόλα:

def linear_algo(items):
    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Η πολυπλοκότητα του linear_algo() Η συνάρτηση είναι γραμμική στο παραπάνω παράδειγμα αφού ο αριθμός των επαναλήψεων του βρόχου for θα είναι ίσο με το μέγεθος της εισόδου items παράταξη. Για παράδειγμα, εάν υπάρχουν 4 στοιχεία στο items λίστα, ο βρόχος for θα εκτελεστεί 4 φορές.

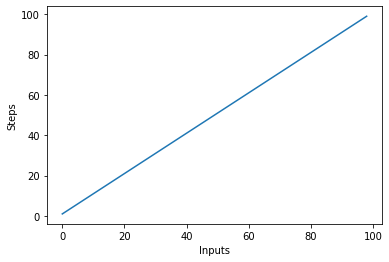
Ας δημιουργήσουμε γρήγορα ένα διάγραμμα για τον αλγόριθμο γραμμικής πολυπλοκότητας με τον αριθμό των εισόδων στον άξονα x και τον αριθμό των βημάτων στον άξονα y:

steps = []
def linear(n):
    return n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

Αυτό θα έχει ως αποτέλεσμα:

Ένα σημαντικό πράγμα που πρέπει να σημειωθεί είναι ότι με μεγάλες εισόδους, οι σταθερές τείνουν να χάνουν την αξία τους. Αυτός είναι ο λόγος για τον οποίο συνήθως αφαιρούμε σταθερές από τη σημείωση Big-O και μια έκφραση όπως O(2n) συνήθως συντομεύεται σε O(n). Τόσο το O(2n) όσο και το O(n) είναι γραμμικά – σημασία έχει η γραμμική σχέση, όχι η συγκεκριμένη τιμή. Για παράδειγμα, ας τροποποιήσουμε το linear_algo():

def linear_algo(items):
    for item in items:
        print(item)

    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Υπάρχουν δύο βρόχοι for που επαναλαμβάνονται πάνω από την είσοδο items λίστα. Επομένως η πολυπλοκότητα του αλγορίθμου γίνεται O (2n), ωστόσο στην περίπτωση άπειρων στοιχείων στη λίστα εισόδου, το διπλάσιο του άπειρου εξακολουθεί να είναι ίσο με το άπειρο. Μπορούμε να αγνοήσουμε τη σταθερά 2 (καθώς είναι τελικά ασήμαντο) και η πολυπλοκότητα του αλγορίθμου παραμένει O (n).

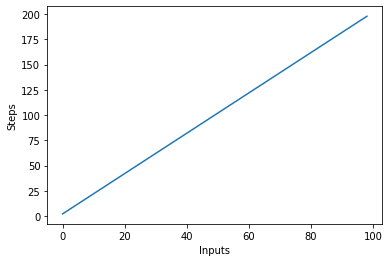
Ας οπτικοποιήσουμε αυτόν τον νέο αλγόριθμο σχεδιάζοντας τις εισόδους στον άξονα Χ και τον αριθμό των βημάτων στον άξονα Υ:

steps = []
def linear(n):
    return 2*n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

Στο παραπάνω σενάριο, μπορείτε να το δείτε ξεκάθαρα y=2n, ωστόσο, η έξοδος είναι γραμμική και μοιάζει με αυτό:

Τετραγωνική πολυπλοκότητα - O(n²)

Η πολυπλοκότητα ενός αλγορίθμου λέγεται ότι είναι τετραγωνική όταν τα βήματα που απαιτούνται για την εκτέλεση ενός αλγορίθμου είναι μια τετραγωνική συνάρτηση του αριθμού των στοιχείων στην είσοδο. Η τετραγωνική πολυπλοκότητα συμβολίζεται ως O(n²):

def quadratic_algo(items):
    for item in items:
        for item2 in items:
            print(item, ' ' ,item2)

quadratic_algo([4, 5, 6, 8])

Έχουμε έναν εξωτερικό βρόχο που επαναλαμβάνει όλα τα στοιχεία στη λίστα εισόδου και στη συνέχεια έναν ένθετο εσωτερικό βρόχο, ο οποίος επαναλαμβάνεται και πάλι σε όλα τα στοιχεία στη λίστα εισόδου. Ο συνολικός αριθμός των βημάτων που εκτελέστηκαν είναι n*n, όπου n είναι ο αριθμός των στοιχείων στον πίνακα εισόδου.

Το παρακάτω γράφημα απεικονίζει τον αριθμό των εισόδων σε σχέση με τα βήματα για έναν αλγόριθμο με τετραγωνική πολυπλοκότητα:

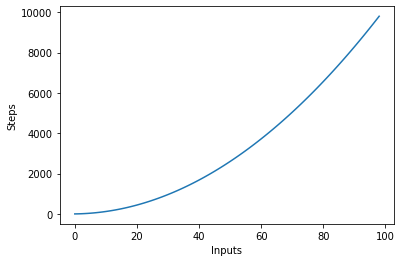
Λογαριθμική πολυπλοκότητα – O (logn)

Ορισμένοι αλγόριθμοι επιτυγχάνουν λογαριθμική πολυπλοκότητα, όπως π.χ Δυαδική αναζήτηση. Η δυαδική αναζήτηση αναζητά ένα στοιχείο σε έναν πίνακα, ελέγχοντας το μέσο ενός πίνακα, και κλάδεμα του μισού στο οποίο δεν βρίσκεται το στοιχείο. Το κάνει ξανά για το υπόλοιπο μισό και συνεχίζει τα ίδια βήματα μέχρι να βρεθεί το στοιχείο. Σε κάθε βήμα, αυτό μισά τον αριθμό των στοιχείων στον πίνακα.

Αυτό απαιτεί να ταξινομηθεί ο πίνακας και να κάνουμε μια υπόθεση σχετικά με τα δεδομένα (όπως ότι έχει ταξινομηθεί).

Όταν μπορείτε να κάνετε υποθέσεις σχετικά με τα εισερχόμενα δεδομένα, μπορείτε να κάνετε βήματα που μειώνουν την πολυπλοκότητα ενός αλγορίθμου. Η λογαριθμική πολυπλοκότητα είναι επιθυμητή, καθώς επιτυγχάνει καλή απόδοση ακόμη και με είσοδο υψηλής κλίμακας.

Εύρεση της πολυπλοκότητας των σύνθετων συναρτήσεων;

Σε προηγούμενα παραδείγματα, είχαμε αρκετά απλές συναρτήσεις στην είσοδο. Ωστόσο, πώς υπολογίζουμε το Big-O των συναρτήσεων που καλούν (πολλαπλές) άλλες συναρτήσεις στην είσοδο;

Ας ρίξουμε μια ματιά:

def complex_algo(items):

    for i in range(5):
        print("Python is awesome")

    for item in items:
        print(item)

    for item in items:
        print(item)

    print("Big O")
    print("Big O")
    print("Big O")

complex_algo([4, 5, 6, 8])

Στο παραπάνω σενάριο εκτελούνται πολλές εργασίες, πρώτα, μια συμβολοσειρά εκτυπώνεται 5 φορές στην κονσόλα χρησιμοποιώντας το print δήλωση. Στη συνέχεια, εκτυπώνουμε τη λίστα εισόδου δύο φορές στην οθόνη και, τέλος, μια άλλη συμβολοσειρά εκτυπώνεται τρεις φορές στην κονσόλα. Για να βρούμε την πολυπλοκότητα ενός τέτοιου αλγορίθμου, πρέπει να αναλύσουμε τον κώδικα του αλγορίθμου σε μέρη και να προσπαθήσουμε να βρούμε την πολυπλοκότητα των μεμονωμένων κομματιών. Σημειώστε την πολυπλοκότητα κάθε κομματιού.

Στην πρώτη ενότητα έχουμε:

for i in range(5):
	print("Python is awesome")

Η πολυπλοκότητα αυτού του μέρους είναι Ο (5) αφού σε αυτό το κομμάτι κώδικα εκτελούνται πέντε σταθερά βήματα ανεξάρτητα από την είσοδο.

Στη συνέχεια, έχουμε:

for item in items:
	print(item)

Γνωρίζουμε ότι η πολυπλοκότητα του παραπάνω κομματιού κώδικα είναι O (n). Ομοίως, η πολυπλοκότητα του παρακάτω κομματιού κώδικα είναι επίσης O (n):

for item in items:
	print(item)

Τέλος, στο παρακάτω κομμάτι κώδικα, μια συμβολοσειρά εκτυπώνεται τρεις φορές, επομένως η πολυπλοκότητα είναι Ο (3):

print("Big O")
print("Big O")
print("Big O")

Για να βρούμε τη συνολική πολυπλοκότητα, πρέπει απλώς να προσθέσουμε αυτές τις επιμέρους πολυπλοκότητες:

O(5) + O(n) + O(n) + O(3)

Απλοποιώντας τα παραπάνω παίρνουμε:

O(8) + O(2n) = O(8+2n)

Είπαμε νωρίτερα ότι όταν η είσοδος (που έχει μήκος n σε αυτή την περίπτωση) γίνει εξαιρετικά μεγάλη, οι σταθερές γίνονται ασήμαντες, δηλαδή το διπλάσιο ή το μισό του άπειρου παραμένει άπειρο. Επομένως, μπορούμε να αγνοήσουμε τις σταθερές. Η τελική πολυπλοκότητα του αλγορίθμου θα είναι O (n)!

Χειρότερη vs Καλύτερη Πολυπλοκότητα υπόθεσης

Συνήθως, όταν κάποιος σας ρωτά για την πολυπλοκότητα ενός αλγορίθμου – ενδιαφέρεται για την πολυπλοκότητα στη χειρότερη περίπτωση (Big-O). Μερικές φορές, μπορεί να ενδιαφέρονται και για την πολυπλοκότητα στην καλύτερη περίπτωση (Big-Omega).

Για να κατανοήσουμε τη σχέση μεταξύ αυτών, ας ρίξουμε μια ματιά σε ένα άλλο κομμάτι κώδικα:

def search_algo(num, items):
    for item in items:
        if item == num:
            return True
        else:
            pass
nums = [2, 4, 6, 8, 10]

print(search_algo(2, nums))

Στο παραπάνω σενάριο, έχουμε μια συνάρτηση που παίρνει έναν αριθμό και μια λίστα αριθμών ως είσοδο. Επιστρέφει true αν ο αριθμός που πέρασε βρεθεί στη λίστα των αριθμών, διαφορετικά, επιστρέφει None. Αν ψάξετε για 2 στη λίστα, θα βρεθεί στην πρώτη σύγκριση. Αυτή είναι η καλύτερη περίπτωση πολυπλοκότητας του αλγορίθμου, καθώς το αντικείμενο που αναζητήθηκε βρίσκεται στο πρώτο ευρετήριο που αναζητήθηκε. Η καλύτερη πολυπλοκότητα των περιπτώσεων, στην προκειμένη περίπτωση, είναι Ο (1). Από την άλλη πλευρά, εάν αναζητήσετε 10, θα βρεθεί στο τελευταίο ευρετήριο που αναζητήσατε. Ως εκ τούτου, ο αλγόριθμος θα πρέπει να πραγματοποιήσει αναζήτηση σε όλα τα στοιχεία της λίστας η πολυπλοκότητα της χειρότερης περίπτωσης γίνεται O (n).

Εκτός από την πολυπλοκότητα της καλύτερης και της χειρότερης περίπτωσης, μπορείτε επίσης να υπολογίσετε η μέση πολυπλοκότητα (Big-Theta) ενός αλγορίθμου, ο οποίος σας λέει "δεδομένης μιας τυχαίας εισαγωγής, ποια είναι η αναμενόμενη χρονική πολυπλοκότητα του αλγορίθμου";

Διαστημική πολυπλοκότητα

Εκτός από τη χρονική πολυπλοκότητα, όπου μετράτε τον αριθμό των βημάτων που απαιτούνται για την ολοκλήρωση της εκτέλεσης ενός αλγορίθμου, μπορείτε επίσης να βρείτε πολυπλοκότητα του χώρου που αναφέρεται στην ποσότητα του χώρου που πρέπει να διαθέσετε στη μνήμη κατά την εκτέλεση ενός προγράμματος.

Ρίξτε μια ματιά στο παρακάτω παράδειγμα:

def return_squares(n):
    square_list = []
    for num in n:
        square_list.append(num * num)

    return square_list

nums = [2, 4, 6, 8, 10]
print(return_squares(nums))

Η return_squares() Η συνάρτηση δέχεται μια λίστα ακεραίων και επιστρέφει μια λίστα με τα αντίστοιχα τετράγωνα. Ο αλγόριθμος πρέπει να εκχωρήσει μνήμη για τον ίδιο αριθμό στοιχείων όπως στη λίστα εισόδου. Επομένως, η χωρική πολυπλοκότητα του αλγορίθμου γίνεται O (n).

Συμπέρασμα

Ο συμβολισμός Big-O είναι η τυπική μέτρηση που χρησιμοποιείται για τη μέτρηση της πολυπλοκότητας ενός αλγορίθμου. Σε αυτόν τον οδηγό, μελετήσαμε τι είναι η σημείωση Big-O και πώς μπορεί να χρησιμοποιηθεί για τη μέτρηση της πολυπλοκότητας μιας ποικιλίας αλγορίθμων. Μελετήσαμε επίσης διαφορετικούς τύπους συναρτήσεων Big-O με τη βοήθεια διαφορετικών παραδειγμάτων Python. Τέλος, εξετάσαμε εν συντομία τη χειρότερη και την καλύτερη περίπτωση πολυπλοκότητας μαζί με την πολυπλοκότητα του χώρου.