Οι μαθηματικοί ρίχνουν ζάρια και παίρνουν βράχο-χαρτί-ψαλίδι

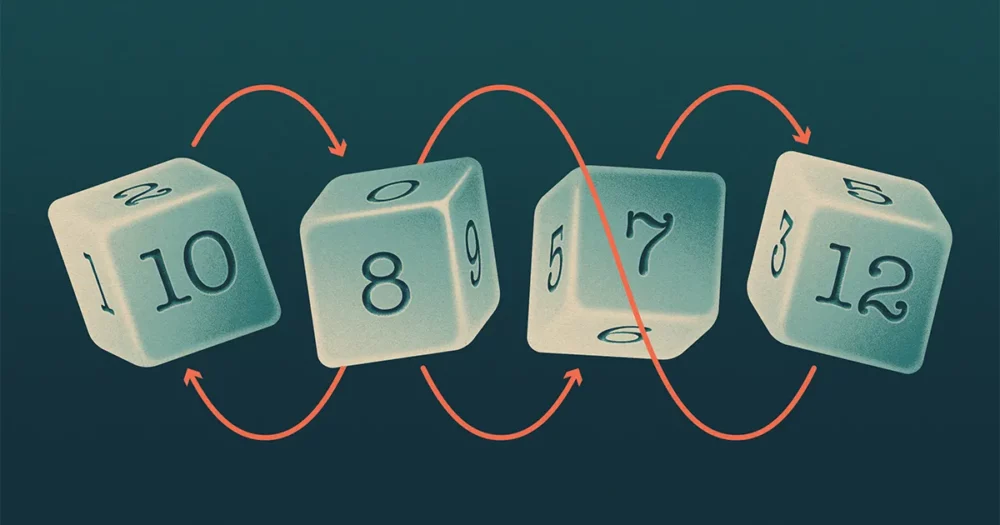
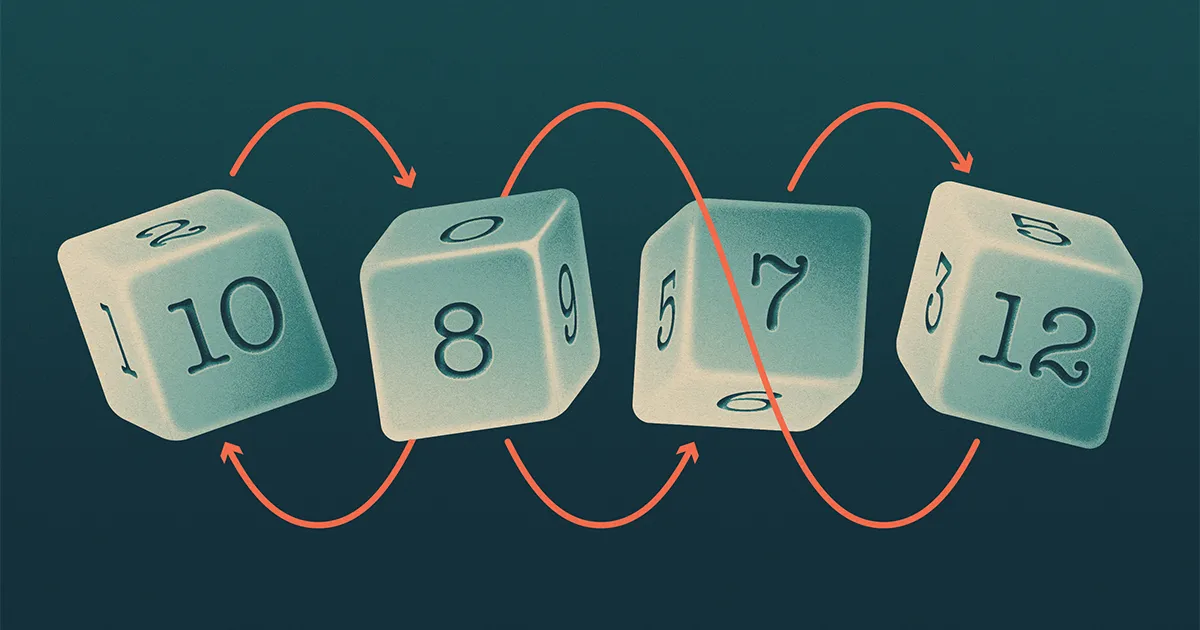
Καθώς ο Bill Gates λέει την ιστορία, ο Warren Buffett τον προκάλεσε κάποτε σε ένα παιχνίδι με ζάρια. Ο καθένας διάλεγε ένα από τα τέσσερα ζάρια που ανήκαν στον Μπάφετ και μετά θα έριχνε, με τον μεγαλύτερο αριθμό να κερδίζει. Αυτά δεν ήταν τυπικά ζάρια - είχαν διαφορετική ποικιλία αριθμών από το συνηθισμένο 1 έως 6. Ο Μπάφετ προσφέρθηκε να αφήσει τον Γκέιτς να επιλέξει πρώτος, ώστε να μπορεί να επιλέξει τον πιο δυνατό ζάρι. Αλλά αφού ο Γκέιτς εξέτασε τα ζάρια, επέστρεψε μια αντιπρόταση: ο Μπάφετ να διαλέξει πρώτος.

Ο Γκέιτς είχε αναγνωρίσει ότι τα ζάρια του Μπάφετ παρουσίαζαν μια περίεργη ιδιότητα: κανένας από αυτούς δεν ήταν ο πιο δυνατός. Αν ο Γκέιτς είχε επιλέξει πρώτος, τότε όποιο ζάρι κι αν διάλεγε, ο Μπάφετ θα μπορούσε να βρει άλλο ζάρι που θα μπορούσε να το ξεπεράσει (δηλαδή με περισσότερες από 50% πιθανότητες να κερδίσει).

Τα τέσσερα ζάρια του Μπάφετ (καλέστε τα A, B, C και D) σχημάτισαν ένα μοτίβο που θύμιζε βραχό-χαρτο-ψαλίδι, στο οποίο A κτυπά B, B κτυπά C, C κτυπά D και D κτυπά A. Οι μαθηματικοί λένε ότι ένα τέτοιο σύνολο ζαριών είναι «αμετάβατο».

«Δεν είναι καθόλου διαισθητικό ότι [αμετάβατα ζάρια] θα έπρεπε καν να υπάρχουν», είπε Μπράιαν Κόνρεϊ, διευθυντής του Αμερικανικού Ινστιτούτου Μαθηματικών (AIM) στο Σαν Χοσέ, ο οποίος έγραψε μια σημαντική εργασία για το θέμα το 2013.

Οι μαθηματικοί κατέληξαν στο πρώτα παραδείγματα αμετάβατων ζαριών πριν από περισσότερα από 50 χρόνια, και τελικά αποδείχθηκε ότι καθώς εξετάζετε τα ζάρια με ολοένα και περισσότερες πλευρές, είναι δυνατό να δημιουργήσετε αμετάβατους κύκλους οποιουδήποτε μήκους. Αυτό που οι μαθηματικοί δεν γνώριζαν μέχρι πρόσφατα ήταν πόσο συνηθισμένα είναι τα αμετάβατα ζάρια. Πρέπει να επινοήσετε τέτοια παραδείγματα προσεκτικά ή μπορείτε να διαλέξετε ζάρια τυχαία και να έχετε μια καλή ευκαιρία να βρείτε ένα αμετάβατο σύνολο;

Κοιτάζοντας τρία ζάρια, αν το ξέρετε αυτό A κτυπά B και B κτυπά C, αυτό φαίνεται σαν απόδειξη A είναι το πιο δυνατό? καταστάσεις όπου C κτυπά A θα πρέπει να είναι σπάνιο. Και πράγματι, εάν οι αριθμοί στα ζάρια επιτρέπεται να αθροιστούν σε διαφορετικά σύνολα, τότε οι μαθηματικοί πιστεύουν ότι αυτή η διαίσθηση ισχύει.

Αλλά α χαρτί που δημοσιεύτηκε στο διαδίκτυο Τα τέλη του περασμένου έτους δείχνει ότι σε ένα άλλο φυσικό περιβάλλον, αυτή η διαίσθηση αποτυγχάνει θεαματικά. Ας υποθέσουμε ότι απαιτείτε τα ζάρια σας να χρησιμοποιούν μόνο τους αριθμούς που εμφανίζονται σε μια κανονική μήτρα και έχουν το ίδιο σύνολο με μια κανονική μήτρα. Τότε, το χαρτί έδειξε, αν A κτυπά B και B κτυπά C, A και C έχουν ουσιαστικά ίσες πιθανότητες να επικρατήσουν μεταξύ τους.

"Γνωρίζοντας ότι A κτυπά B και B κτυπά C απλά δεν σας δίνει πληροφορίες για το αν A κτυπά C," είπε Τιμότι Γκίβερς του Πανεπιστημίου του Κέιμπριτζ, κάτοχος του μεταλλίου Fields και ένας από τους συντελεστές του νέου αποτελέσματος, το οποίο αποδείχθηκε μέσω μιας ανοιχτής διαδικτυακής συνεργασίας γνωστής ως έργο Polymath.

Εν τω μεταξύ, ένα άλλο πρόσφατο έγγραφο αναλύει σετ από τέσσερα ή περισσότερα ζάρια. Αυτό το εύρημα είναι αναμφισβήτητα ακόμη πιο παράδοξο: Αν, για παράδειγμα, διαλέξετε τέσσερα ζάρια τυχαία και διαπιστώσετε ότι A κτυπά B, B κτυπά C και C κτυπά D, τότε είναι ελαφρώς περισσότερο πιθανό για D να νικήσει A από το αντίστροφο.

Ούτε δυνατός ούτε αδύναμος

Το πρόσφατο εξάνθημα των αποτελεσμάτων ξεκίνησε πριν από περίπου μια δεκαετία, αφού ο Conrey παρακολούθησε μια συγκέντρωση για δασκάλους μαθηματικών με μια συνεδρία που κάλυψε αμετάβατα ζάρια. «Δεν είχα ιδέα ότι θα μπορούσαν να υπάρχουν τέτοια πράγματα», είπε. «Με γοήτευσαν κάπως».

Αποφάσισε (αργότερα ενώθηκε και ο συνάδελφός του Κεντ Μόρισον στο AIM) για να εξερευνήσει το θέμα με τρεις μαθητές γυμνασίου που καθοδηγούσε — τον James Gabbard, την Katie Grant και τον Andrew Liu. Πόσο συχνά, αναρωτήθηκε η ομάδα, τα τυχαία επιλεγμένα ζάρια θα σχηματίσουν έναν αμετάβατο κύκλο;

Τα μη μεταβατικά σετ ζαριών πιστεύεται ότι είναι σπάνια εάν οι αριθμοί των όψεων των ζαριών αθροίζονται σε διαφορετικά σύνολα, καθώς το ζάρι με το υψηλότερο σύνολο είναι πιθανό να νικήσει τους άλλους. Έτσι, η ομάδα αποφάσισε να επικεντρωθεί σε ζάρια που έχουν δύο ιδιότητες: Πρώτον, τα ζάρια χρησιμοποιούν τους ίδιους αριθμούς όπως σε ένα τυπικό ζάρι — 1 έως n, στην περίπτωση ενός n-πλευρικό ζάρι. Και δεύτερον, οι αριθμοί προσώπων αθροίζονται στο ίδιο σύνολο όπως σε μια τυπική μήτρα. Αλλά σε αντίθεση με τα τυπικά ζάρια, κάθε ζάρι μπορεί να επαναλαμβάνει μερικούς από τους αριθμούς και να αφήνει έξω άλλους.

Στην περίπτωση των ζαριών έξι όψεων, υπάρχουν μόνο 32 διαφορετικά ζάρια που έχουν αυτές τις δύο ιδιότητες. Έτσι, με τη βοήθεια ενός υπολογιστή, η ομάδα μπορούσε να εντοπίσει όλες τις τριάδες στις οποίες A κτυπά B και B κτυπά C. Οι ερευνητές διαπίστωσαν, προς έκπληξή τους, ότι A κτυπά C σε 1,756 τριπλάσια και C κτυπά A σε 1,731 τριάδες — σχεδόν πανομοιότυποι αριθμοί. Με βάση αυτόν τον υπολογισμό και τις προσομοιώσεις ζαριών με περισσότερες από έξι πλευρές, υπέθεσε η ομάδα ότι καθώς ο αριθμός των πλευρών στα ζάρια πλησιάζει στο άπειρο, η πιθανότητα A κτυπά C πλησιάζει το 50%.

Η εικασία, με το μείγμα προσβασιμότητας και αποχρώσεων, έπληξε τον Conrey ως καλή τροφή για ένα έργο Polymath, στο οποίο πολλοί μαθηματικοί συγκεντρώνονται στο διαδίκτυο για να μοιραστούν ιδέες. Στα μέσα του 2017, πρότεινε την ιδέα στον Gowers, τον εμπνευστή της προσέγγισης Polymath. «Μου άρεσε πολύ η ερώτηση, λόγω της αξίας της έκπληξης», είπε ο Gowers. Έγραψε α ανάρτηση σχετικά με την εικασία που προσέλκυσε μια αναταραχή σχολίων, και κατά τη διάρκεια έξι επιπλέον αναρτήσεων, οι σχολιαστές κατάφεραν να το αποδείξουν.

Στην εργασία τους, Δημοσιεύτηκε ηλεκτρονικά στα τέλη Νοεμβρίου 2022, ένα βασικό μέρος της απόδειξης περιλαμβάνει το να δείξουμε ότι, ως επί το πλείστον, δεν έχει νόημα να μιλάμε για το εάν ένα μόνο ζάρι είναι ισχυρό ή αδύναμο. Τα ζάρια του Buffett, κανένα από τα οποία δεν είναι το πιο δυνατό του πακέτου, δεν είναι και τόσο ασυνήθιστα: Εάν επιλέξετε ένα ζάρι τυχαία, έδειξε το έργο Polymath, είναι πιθανό να κερδίσει περίπου τα μισά από τα άλλα ζάρια και να χάσει από το άλλο μισό. «Σχεδόν κάθε ζάρι είναι αρκετά μέτριο», είπε ο Gowers.

Το έργο διέφερε από το αρχικό μοντέλο της ομάδας AIM από μία άποψη: Για να απλοποιηθούν ορισμένες τεχνικές λεπτομέρειες, το έργο δήλωσε ότι η σειρά των αριθμών σε ένα ζάρι έχει σημασία — έτσι, για παράδειγμα, το 122556 και το 152562 θα θεωρούνταν δύο διαφορετικά ζάρια. Αλλά το αποτέλεσμα του Polymath, σε συνδυασμό με τα πειραματικά στοιχεία της ομάδας AIM, δημιουργεί μια ισχυρή υπόθεση ότι η εικασία ισχύει και στο αρχικό μοντέλο, είπε ο Gowers.

«Ήμουν απόλυτα ευχαριστημένος που βρήκαν αυτή την απόδειξη», είπε ο Conrey.

Όταν επρόκειτο για συλλογές τεσσάρων ή περισσότερων ζαριών, η ομάδα AIM είχε προβλέψει παρόμοια συμπεριφορά με αυτή των τριών ζαριών: Για παράδειγμα, αν A κτυπά B, B κτυπά C και C κτυπά D τότε θα πρέπει να υπάρχει περίπου 50-50 πιθανότητα αυτό D κτυπά A, πλησιάζοντας ακριβώς το 50-50 καθώς ο αριθμός των πλευρών στα ζάρια πλησιάζει στο άπειρο.

Για να δοκιμάσουν τις εικασίες, οι ερευνητές προσομοίωσαν τουρνουά head-to-head για σετ τεσσάρων ζαριών με 50, 100, 150 και 200 ​​πλευρές. Οι προσομοιώσεις δεν υπάκουσαν στις προβλέψεις τους τόσο πολύ όσο στην περίπτωση των τριών ζαριών, αλλά ήταν ακόμα αρκετά κοντά για να ενισχύσουν την πίστη τους στην εικασία. Αλλά αν και οι ερευνητές δεν το συνειδητοποίησαν, αυτές οι μικρές αποκλίσεις έφεραν ένα διαφορετικό μήνυμα: Για σετ τεσσάρων ή περισσότερων ζαριών, η εικασία τους είναι ψευδής.

«Θέλαμε πραγματικά [η εικασία] να είναι αληθινή, γιατί θα ήταν ωραίο», είπε ο Conrey.

Στην περίπτωση τεσσάρων ζαριών, Elisabetta Cornacchia του Ελβετικού Ομοσπονδιακού Ινστιτούτου Τεχνολογίας της Λωζάνης και Jan Hązła του Αφρικανικού Ινστιτούτου Μαθηματικών Επιστημών στο Κιγκάλι της Ρουάντα, έδειξε στο α χαρτί δημοσιεύτηκε στο διαδίκτυο στα τέλη του 2020 ότι εάν A κτυπά B, B κτυπά C και C κτυπά D, Τότε D έχει λίγο περισσότερες από 50% πιθανότητες να νικήσει A — μάλλον κάπου γύρω στο 52%, είπε ο Hązła. (Όπως και με το χαρτί Polymath, οι Cornacchia και Hązła χρησιμοποίησαν ένα ελαφρώς διαφορετικό μοντέλο από το χαρτί AIM.)

Το εύρημα των Cornacchia και Hązła προκύπτει από το γεγονός ότι, παρόλο που, κατά κανόνα, ένα μεμονωμένο ζάρι δεν θα είναι ούτε δυνατό ούτε αδύναμο, ένα ζευγάρι ζάρια μπορεί μερικές φορές να έχει κοινούς τομείς δύναμης. Εάν διαλέξετε δύο ζάρια τυχαία, έδειξαν οι Cornacchia και Hązła, υπάρχει μια αξιοπρεπής πιθανότητα τα ζάρια να συσχετιστούν: Θα τείνουν να νικήσουν ή να χάσουν στα ίδια ζάρια. «Αν σας ζητήσω να δημιουργήσετε δύο ζάρια που να είναι κοντά το ένα στο άλλο, αποδεικνύεται ότι αυτό είναι δυνατό», είπε ο Hązła. Αυτές οι μικρές τσέπες συσχέτισης ωθούν τα αποτελέσματα του τουρνουά μακριά από τη συμμετρία μόλις υπάρχουν τουλάχιστον τέσσερα ζάρια στην εικόνα.

Τα πρόσφατα έγγραφα δεν είναι το τέλος της ιστορίας. Η εργασία των Cornacchia και Hązła αρχίζει να αποκαλύπτει ακριβώς πώς οι συσχετισμοί μεταξύ των ζαριών αποδυναμώνουν τη συμμετρία των τουρνουά. Εν τω μεταξύ, ωστόσο, γνωρίζουμε τώρα ότι υπάρχουν πολλά σετ αμετάβατων ζαριών εκεί έξω - ίσως ακόμη και ένα που είναι αρκετά λεπτό για να ξεγελάσει τον Μπιλ Γκέιτς να επιλέξει πρώτος.