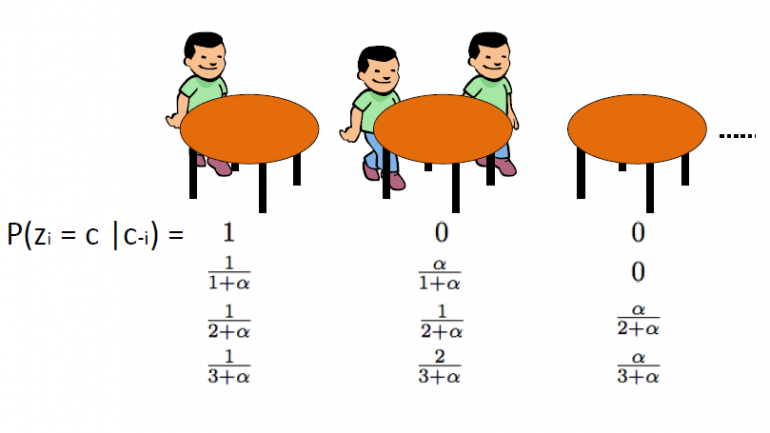Η διαδικασία Dirichlet η κινεζική διαδικασία εστιατορίων και άλλες παραστάσεις

• 20 Μαΐου 2014
• Βασίλης Βρυνιώτης
• . Χωρίς σχόλια

Αυτό το άρθρο είναι το τρίτο μέρος της σειράς για Ομαδοποίηση με Μοντέλα Μιγμάτων Διεργασιών Dirichlet. Την προηγούμενη φορά ορίσαμε το μοντέλο πεπερασμένου μείγματος με βάση την κατανομή Dirichlet και θέσαμε ερωτήσεις για το πώς μπορούμε να κάνουμε αυτό το συγκεκριμένο μοντέλο άπειρο. Συζητήσαμε εν συντομία την ιδέα να πάρουμε το όριο του μοντέλου όταν ο αριθμός k των συστάδων τείνει στο άπειρο, αλλά όπως τονίσαμε η ύπαρξη ενός τέτοιου αντικειμένου δεν είναι ασήμαντη (με άλλα λόγια, πώς στην πραγματικότητα «παίρνουμε το όριο ενός μοντέλου ”;). Για υπενθύμιση, ο λόγος για τον οποίο θέλουμε να πάρουμε το k άπειρο είναι επειδή με αυτόν τον τρόπο θα έχουμε ένα μη παραμετρικό μοντέλο που δεν απαιτεί να προκαθορίσουμε τον συνολικό αριθμό των συστάδων εντός των δεδομένων.

Ενημέρωση: Το Datumbox Machine Learning Framework είναι τώρα ανοιχτού κώδικα και δωρεάν κατεβάσετε. Ρίξτε μια ματιά στο πακέτο com.datumbox.framework.machinelearning.clustering για να δείτε την υλοποίηση Dirichlet Process Mixture Models στην Java.

Παρόλο που ο στόχος μας είναι να δημιουργήσουμε ένα μοντέλο που να είναι ικανό να εκτελεί ομαδοποίηση σε σύνολα δεδομένων, πριν από αυτό πρέπει να συζητήσουμε για τις διεργασίες Dirichlet. Θα παρέχουμε τόσο τους αυστηρούς μαθηματικούς ορισμούς όσο και τις πιο εύχρηστες εξηγήσεις του DP και θα συζητήσουμε τρόπους κατασκευής της διαδικασίας. Αυτές οι κατασκευές/παραστάσεις μπορούν να θεωρηθούν ως ένας τρόπος εύρεσης περιπτώσεων της διαδικασίας Dirichlet στην «πραγματική ζωή».

Παρά το γεγονός ότι προσπάθησα να προσαρμόσω την ερευνητική μου έκθεση με τέτοιο τρόπο ώστε αυτές οι αναρτήσεις ιστολογίου να είναι ευκολότερες στην παρακολούθηση, εξακολουθεί να είναι σημαντικό να ορίσουμε τα απαραίτητα μαθηματικά εργαλεία και κατανομές πριν προχωρήσουμε στη χρήση των μοντέλων. Τα μοντέλα της διεργασίας Dirichlet αποτελούν θέμα ενεργούς έρευνας, αλλά απαιτούν καλή κατανόηση της Στατιστικής και των Στοχαστικών Διαδικασιών πριν από τη χρήση τους. Ένα άλλο πρόβλημα είναι ότι, όπως θα δούμε σε αυτό το άρθρο, οι διεργασίες Dirichlet μπορούν να αναπαρασταθούν/κατασκευαστούν με πολλούς τρόπους. Ως αποτέλεσμα, αρκετές ακαδημαϊκές εργασίες χρησιμοποιούν εντελώς διαφορετικές σημειώσεις/συμβάσεις και εξετάζουν το πρόβλημα από διαφορετικές οπτικές γωνίες. Σε αυτήν την ανάρτηση προσπαθώ να τα εξηγήσω όσο πιο απλά γίνεται και να χρησιμοποιήσω την ίδια σημείωση. Ας ελπίσουμε ότι τα πράγματα θα γίνουν πιο ξεκάθαρα με τα δύο προσεχή άρθρα που επικεντρώνονται στον ορισμό των μοντέλων μιγμάτων διεργασιών Dirichlet και στον τρόπο χρήσης τους για την πραγματοποίηση ανάλυσης συστάδων.

1. Ορισμός της διαδικασίας Dirichlet

Μια διεργασία Dirichlet σε έναν χώρο Θ είναι μια στοχαστική διαδικασία. Είναι μια κατανομή πιθανότητας σε «κατανομές πιθανοτήτων πάνω από το χώρο Θ» και α αντλούμε από αυτό είναι μια διακριτή κατανομή. Πιο επίσημα μια διανομή Dirichlet είναι μια κατανομή σε μέτρα πιθανότητας. ΕΝΑ μέτρο πιθανότητας είναι συνάρτηση υποσυνόλων του χώρου Θ έως [0,1]. Το G είναι ένα κατανεμημένο μέτρο τυχαίας πιθανότητας DP, που συμβολίζεται ως , εάν πρόκειται για οποιοδήποτε διαμέρισμα (Α₁,…ΕΝΑ_n) του χώρου Θ έχουμε ότι .

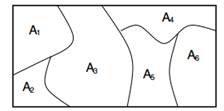
Σχήμα 1: Τα περιθώρια σε πεπερασμένα χωρίσματα κατανέμονται Dirichlet.

Το DP έχει δύο παραμέτρους: Η πρώτη είναι η βασική κατανομή G₀ που χρησιμεύει σαν μέσο . Η δεύτερη είναι η παράμετρος ισχύος α που είναι αυστηρά θετική και λειτουργεί σαν αντίστροφη διακύμανση . Καθορίζει την έκταση της επανάληψης των τιμών της κατανομής εξόδου. Όσο μεγαλύτερη είναι η τιμή του α, τόσο μικρότερη είναι η επανάληψη. Όσο μικρότερη είναι η τιμή, τόσο μεγαλύτερη είναι η επανάληψη των τιμών κατανομής εξόδου. Τέλος ο χώρος Θ είναι ο χώρος παραμέτρων στον οποίο ορίζουμε το DP. Επιπλέον, ο χώρος Θ είναι επίσης ο ορισμός του G₀ που είναι ίδιο με αυτό του Γ.

Ένα πιο απλό και περισσότερο διαισθητικό τρόπο για να εξηγήσουμε μια διαδικασία Dirichlet είναι η εξής. Ας υποθέσουμε ότι έχουμε ένα χώρο Θ που μπορεί να χωριστεί με οποιονδήποτε πεπερασμένο τρόπο (Α₁,…,ΕΝΑ_n) και μια κατανομή πιθανοτήτων G που τους εκχωρεί πιθανότητες. Το G είναι μια συγκεκριμένη κατανομή πιθανότητας πάνω από το Θ, αλλά υπάρχουν πολλές άλλες. Η διαδικασία Dirichlet στο Θ μοντελοποιεί ακριβώς αυτό. είναι μια κατανομή σε όλες τις πιθανές κατανομές στο χώρο Θ. Η διαδικασία Dirichlet παραμετροποιείται με το G₀ συνάρτηση βάσης και την παράμετρο συγκέντρωσης α. Μπορούμε να πούμε ότι το G κατανέμεται σύμφωνα με το DP με τις παραμέτρους α και G₀ αν η κοινή κατανομή των πιθανοτήτων που αποδίδει ο G στις διαιρέσεις του Θ ακολουθεί την Κατανομή Dirichlet. Εναλλακτικά μπορούμε να πούμε ότι οι πιθανότητες που εκχωρεί το G σε οποιαδήποτε πεπερασμένη κατάτμηση του Θ ακολουθούν την Κατανομή Dirichlet.

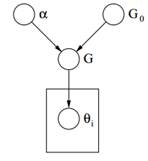
Εικόνα 2: Γραφικό Μοντέλο Διεργασίας Dirichlet

Τέλος παραπάνω μπορούμε να δούμε το γραφικό μοντέλο ενός DP. Θα πρέπει να σημειώσουμε ότι το α είναι μια βαθμωτή υπερπαράμετρος, G₀ είναι η βασική κατανομή του DP, G μια τυχαία κατανομή στο χώρο παραμέτρων Θ που δειγματίστηκε από το DP που εκχωρεί πιθανότητες στις παραμέτρους και θ_i είναι ένα διάνυσμα παραμέτρου που προέρχεται από την κατανομή G και είναι στοιχείο του χώρου Θ.

2. Οπίσθια διεργασίες Dirichlet

Οι διεργασίες του μεταγενέστερου Dirichlet συζητήθηκαν από Φέργκιουσον. Ξεκινάμε σχεδιάζοντας ένα τυχαίο μέτρο πιθανότητας G από μια διαδικασία Dirichlet, . Δεδομένου ότι το G είναι μια κατανομή πιθανότητας στο Θ, μπορούμε επίσης να κάνουμε δείγμα από αυτήν την κατανομή και να αντλήσουμε ανεξάρτητα πανομοιότυπα κατανεμημένα δείγματα θ₁,…, θ_n ~ G. Δεδομένου ότι οι αντλήσεις από μια διαδικασία Dirichlet είναι διακριτές κατανομές, μπορούμε να αναπαραστήσουμε όπου είναι μια σύντομη σημειογραφία για που είναι μια συνάρτηση δέλτα που παίρνει 1 εάν και 0 αλλού. Ένα ενδιαφέρον αποτέλεσμα αυτού είναι ότι εφόσον το G ορίζεται με αυτόν τον τρόπο, υπάρχει θετική πιθανότητα διαφορετικά δείγματα να έχουν την ίδια τιμή . Όπως θα δούμε στη συνέχεια, αυτό δημιουργεί ένα εφέ ομαδοποίησης που μπορεί να χρησιμοποιηθεί για την εκτέλεση Ανάλυσης συμπλέγματος σε σύνολα δεδομένων.

Χρησιμοποιώντας τους παραπάνω ορισμούς και παρατηρήσεις, θέλουμε να υπολογίσουμε το οπίσθιο μέρος της διαδικασίας Dirichlet με βάση τα δείγματα θ. Παρόλα αυτά αφού το ξέρουμε και χρησιμοποιώντας τους κανόνες Bayes και τη σύζευξη μεταξύ Dirichlet και Πολυωνυμικού έχουμε αυτό και .

Εξίσωση 1: Οπίσθια διεργασία Dirichlet

Αυτή η ιδιότητα είναι πολύ σημαντική και χρησιμοποιείται από τις διάφορες αναπαραστάσεις DP.

3. Αναπαραστάσεις της διαδικασίας Dirichlet

Στα προηγούμενα τμήματα ορίσαμε τη Διαδικασία Dirichlet και παρουσιάσαμε το θεωρητικό της μοντέλο. Ένα σημαντικό ερώτημα που πρέπει να απαντήσουμε είναι πώς γνωρίζουμε ότι υπάρχει ένα τέτοιο αντικείμενο και πώς μπορούμε κατασκευάζουν και αναπαριστούν μια διαδικασία Dirichlet.

Οι πρώτες ενδείξεις ύπαρξης δόθηκαν από Φέργκιουσον ο οποίος χρησιμοποίησε το Θεώρημα Συνέπειας Kolmogorov, έδωσε τον ορισμό της Διεργασίας Dirichlet και περιέγραψε την Οπίσθια Διαδικασία Dirichlet. Συνεχίζοντας την έρευνά του, Blackwell και MacQueen χρησιμοποίησε το Θεώρημα του de Finetti για να αποδείξει την ύπαρξη ενός τέτοιου τυχαίου μέτρου πιθανότητας και εισήγαγε το σχήμα δοχείων Blackwell-MacQueen που ικανοποιεί τις ιδιότητες της διαδικασίας Dirichlet. Το 1994 Σεθουραμάν παρείχε έναν πρόσθετο απλό και άμεσο τρόπο κατασκευής ενός DP με την εισαγωγή της κατασκευής Stick-breaking. Τέλος, μια άλλη εκπροσώπηση παρασχέθηκε από Aldous ο οποίος εισήγαγε τη διαδικασία του κινέζικου εστιατορίου ως έναν αποτελεσματικό τρόπο κατασκευής μιας διαδικασίας Dirichlet.

Οι διάφορες αναπαραστάσεις της διαδικασίας Dirichlet είναι μαθηματικά ισοδύναμες αλλά η διατύπωσή τους διαφέρει επειδή εξετάζουν το πρόβλημα από διαφορετικές οπτικές γωνίες. Παρακάτω παρουσιάζουμε τις πιο κοινές αναπαραστάσεις που υπάρχουν στη βιβλιογραφία και επικεντρωνόμαστε στη διαδικασία κινέζικου εστιατορίου που παρέχει έναν απλό και υπολογιστικά αποδοτικό τρόπο κατασκευής αλγορίθμων συμπερασμάτων για τη διαδικασία Dirichlet.

3.1 Το σχήμα δοχείων Blackwell-MacQueen

Το σχήμα δοχείων Blackwell-MacQueen μπορεί να χρησιμοποιηθεί για να αναπαραστήσει μια διαδικασία Dirichlet και εισήχθη από Blackwell και MacQueen. Βασίζεται στο σχήμα Pólya urn που μπορεί να θεωρηθεί ως το αντίθετο μοντέλο δειγματοληψίας χωρίς αντικατάσταση. Στο σχήμα Pólya urn υποθέτουμε ότι έχουμε ένα αδιαφανές δοχείο που περιέχει χρωματιστές μπάλες και σχεδιάζουμε μπάλες τυχαία. Όταν σχεδιάζουμε μια μπάλα, παρατηρούμε το χρώμα της, την ξαναβάζουμε στη λάρνακα και προσθέτουμε μια επιπλέον μπάλα του ίδιου χρώματος. Ένα παρόμοιο σχήμα χρησιμοποιείται από τους Blackwell και MacQueen για την κατασκευή μιας διαδικασίας Dirichlet.

Αυτό το σχήμα παράγει μια ακολουθία θ₁,θ₂,… με υπό όρους πιθανότητες . Σε αυτό το σχήμα υποθέτουμε ότι ο Γ₀ είναι μια κατανομή στα χρώματα και κάθε θ_n αντιπροσωπεύει το χρώμα της μπάλας που τοποθετείται στο δοχείο. ο αλγόριθμος είναι όπως ακολουθεί:

· Ξεκινάμε με ένα άδειο δοχείο.

· Με πιθανότητα ανάλογη του α σχεδιάζουμε και προσθέτουμε μια μπάλα αυτού του χρώματος στη λάρνακα.

· Με πιθανότητα ανάλογη του n-1 βγάζουμε μια τυχαία μπάλα από τη λάρνακα, παρατηρούμε το χρώμα της, την τοποθετούμε πίσω στη λάρνακα και προσθέτουμε μια επιπλέον μπάλα του ίδιου χρώματος στη λάρνακα.

Προηγουμένως ξεκινήσαμε με μια διαδικασία Dirichlet και αντλήσαμε το σχήμα Blackwell-MacQueen. Τώρα ας ξεκινήσουμε αντίστροφα από το σχήμα Blackwell-MacQueen και ας εξάγουμε το DP. Εφόσον το θ_i έχουν ληφθεί με τρόπο iid από το G, η κοινή τους κατανομή θα είναι αμετάβλητη σε οποιεσδήποτε πεπερασμένες μεταθέσεις και επομένως είναι ανταλλάξιμα. Συνεπώς, χρησιμοποιώντας το θεώρημα του de Finetti, έχουμε ότι πρέπει να υπάρχει μια κατανομή στα μέτρα για να γίνουν iid και αυτή η κατανομή είναι η Διαδικασία Dirichlet. Ως αποτέλεσμα, αποδεικνύουμε ότι το σχήμα δοχείων Blackwell-MacQueen είναι μια αναπαράσταση του DP και μας δίνει έναν συγκεκριμένο τρόπο να το κατασκευάσουμε. Όπως θα δούμε αργότερα, αυτό το σχήμα είναι μαθηματικά ισοδύναμο με τη διαδικασία κινέζικου εστιατορίου.

3.2 Η κατασκευή που σπάει το ραβδί

Η κατασκευή που σπάει το ραβδί είναι ένας εναλλακτικός τρόπος για να αναπαραστήσουμε μια διαδικασία Dirichlet που εισήχθη από Σεθουραμάν. Είναι ένας εποικοδομητικός τρόπος διαμόρφωσης του διανομή και χρησιμοποιεί το ακολουθώντας την αναλογία: Υποθέτουμε ότι έχουμε ένα ραβδί μήκους 1, το σπάμε στη θέση β₁ και αναθέτουμε π₁ ίσο με το μήκος του μέρους του ραβδιού που σπάσαμε. Επαναλαμβάνουμε την ίδια διαδικασία για να πάρουμε το π₂, π₃,… και τα λοιπά; λόγω του τρόπου με τον οποίο ορίζεται αυτό το σχήμα μπορούμε να συνεχίσουμε να το κάνουμε άπειρες φορές.

Με βάση τα παραπάνω το π_k μπορεί να μοντελοποιηθεί ως , Όπου η ενώ όπως και στα προηγούμενα σχήματα τα θ δειγματίζονται απευθείας από την κατανομή Βάσης . Συνεπώς η κατανομή G μπορεί να γραφτεί ως άθροισμα συναρτήσεων δέλτα σταθμισμένη με π_k πιθανότητες που είναι ίσες με . Έτσι, η κατασκευή που σπάει το ραβδί μας δίνει έναν απλό και διαισθητικό τρόπο να κατασκευάσουμε μια διαδικασία Dirichlet.

3.3 Η διαδικασία του κινέζικου εστιατορίου

Η διαδικασία κινέζικου εστιατορίου, η οποία εισήχθη από Aldous, είναι ένας άλλος αποτελεσματικός τρόπος αναπαράστασης μιας διαδικασίας Dirichlet και μπορεί να συνδεθεί απευθείας με το σχήμα δοχείων Blackwell-MacQueen. Αυτό το σχήμα χρησιμοποιεί το ακολουθώντας την αναλογία: Υποθέτουμε ότι υπάρχει ένα κινέζικο εστιατόριο με άπειρα τραπέζια. Καθώς οι πελάτες εισέρχονται στο εστιατόριο κάθονται τυχαία σε οποιοδήποτε από τα κατειλημμένα τραπέζια ή επιλέγουν να καθίσουν στο πρώτο διαθέσιμο άδειο τραπέζι.

Το CRP ορίζει μια κατανομή στο χώρο των διαμερισμάτων των θετικών ακεραίων. Ξεκινάμε σχεδιάζοντας θ₁,…θ_n από το σχήμα δοχείων Blackwell-MacQueen. Όπως συζητήσαμε στα προηγούμενα τμήματα, αναμένουμε να δούμε ένα φαινόμενο ομαδοποίησης και έτσι ο συνολικός αριθμός των μοναδικών θ τιμών k θα είναι σημαντικά μικρότερος από n. Έτσι αυτό ορίζει μια κατάτμηση του συνόλου {1,2,…,n} σε k συμπλέγματα. Κατά συνέπεια, η σχεδίαση από το σχήμα urn Blackwell-MacQueen προκαλεί μια τυχαία κατάτμηση του συνόλου {1,2,…,n}. Η διαδικασία του κινέζικου εστιατορίου είναι αυτή που προκαλείται διανομή σε χωρίσματα. Ο αλγόριθμος είναι ο εξής:

· Ξεκινάμε με ένα άδειο εστιατόριο.

· η 1^st ο πελάτης κάθεται πάντα στο 1^st τραπέζι

· Το ν+1^th Ο πελάτης έχει 2 επιλογές:

o Καθίστε στο 1ο αδιάθετο τραπέζι με πιθανότητα

o Καθίστε σε οποιοδήποτε από τα kth κατειλημμένα τραπέζια με πιθανότητα
όπου είναι ο αριθμός των ατόμων που κάθονται σε αυτό το τραπέζι

Όπου α είναι η τιμή διασποράς του DP και n ο συνολικός αριθμός πελατών στο εστιατόριο σε μια δεδομένη στιγμή. Η λανθάνουσα μεταβλητή z_i αποθηκεύει τον αριθμό του πίνακα του i^th πελάτη και παίρνει τιμές από 1 έως k_n όπου κ_n είναι ο συνολικός αριθμός κατειλημμένων τραπεζιών όταν n πελάτες βρίσκονται στο εστιατόριο. Να σημειώσουμε ότι το κ_n θα είναι πάντα μικρότερο ή ίσο με n και κατά μέσο όρο είναι περίπου . Τέλος να σημειώσουμε ότι η πιθανότητα τακτοποίησης τραπεζιού είναι αμετάβλητο στις μεταθέσεις. Έτσι το z_i είναι ανταλλάξιμα που σημαίνει ότι οι πίνακες με το ίδιο μέγεθος πελατών έχουν την ίδια πιθανότητα.

Η διαδικασία κινέζικου εστιατορίου είναι στενά συνδεδεμένη με το σχέδιο Pólya urn και τη διαδικασία Dirichlet. Το CRP είναι ένας τρόπος για να ορίσετε α διανομή σε χωρίσματα (αναθέσεις πίνακα) n σημείων και μπορούν να χρησιμοποιηθούν ως προηγούμενα στον χώρο της λανθάνουσας μεταβλητής z_i Ποιό καθορίζει τις αναθέσεις συστάδων. Το CRP είναι ισοδύναμο με το σχήμα urn του Pólya με μόνη διαφορά ότι δεν εκχωρεί παραμέτρους σε κάθε πίνακα/σύμπλεγμα. Να πάω από το CRP στο σχέδιο άρτου Pólya σχεδιάζουμε για όλους τους πίνακες k=1,2… και μετά για κάθε x_i που ομαδοποιείται στον πίνακα z_i εκχωρώ α . Με άλλα λόγια αντιστοιχίστε στο νέο x_i την παράμετρο θ του πίνακα. Τελικά από τότε δεν μπορούμε να αναθέσουμε το θ σε άπειρους πίνακες από την αρχή, μπορούμε απλώς να αντιστοιχίσουμε ένα νέο θ κάθε φορά που κάποιος κάθεται σε ένα νέο τραπέζι. Λόγω όλων των παραπάνω, το CRP μπορεί να μας βοηθήσει να δημιουργήσουμε υπολογιστικά αποδοτικούς αλγόριθμους για την εκτέλεση Ανάλυσης Cluster σε σύνολα δεδομένων.

Σε αυτήν την ανάρτηση, συζητήσαμε τη Διαδικασία Dirichlet και διάφορους τρόπους κατασκευής της. Θα χρησιμοποιήσουμε τις παραπάνω ιδέες στο επόμενο άρθρο. Θα εισαγάγουμε το Μοντέλο Μείγματος Διεργασίας Dirichlet και θα χρησιμοποιήσουμε την Αναπαράσταση Κινέζικου Εστιατορίου για να κατασκευάσουμε τη Διαδικασία Dirichlet και να προδιαμορφώσουμε την Ανάλυση Συστάδων. Εάν χάσατε μερικά σημεία, μην ανησυχείτε, καθώς τα πράγματα θα αρχίσουν να γίνονται πιο ξεκάθαρα με τα επόμενα δύο άρθρα.

Ελπίζω να σας φάνηκε ενδιαφέρουσα αυτή η ανάρτηση. Εάν το κάνατε, αφιερώστε λίγο χρόνο για να το μοιραστείτε στο Facebook και στο Twitter. 🙂