Χρήση τεχνητής νοημοσύνης για την επίλυση του παιχνιδιού 2048 (κώδικας JAVA)

• Απρίλιος 7, 2014
• Βασίλης Βρυνιώτης
• . 6 Σχόλια

Μέχρι τώρα οι περισσότεροι από εσάς έχετε ακούσει/παίξει το 2048 παιχνίδι από τον Gabriele Cirulli. Είναι ένα απλό αλλά εξαιρετικά εθιστικό επιτραπέζιο παιχνίδι που απαιτεί να συνδυάσετε τους αριθμούς των κελιών για να φτάσετε στον αριθμό 2048. Όπως ήταν αναμενόμενο, η δυσκολία του παιχνιδιού αυξάνεται καθώς περισσότερα κελιά γεμίζουν με υψηλές τιμές. Προσωπικά, παρόλο που αφιέρωσα αρκετό χρόνο παίζοντας το παιχνίδι, δεν μπόρεσα ποτέ να φτάσω το 2048. Το φυσικό πράγμα που πρέπει να κάνουμε είναι να προσπαθήσουμε να αναπτύξουμε έναν λύτη τεχνητής νοημοσύνης στην JAVA για να κερδίσουμε το παιχνίδι του 2048. 🙂

Σε αυτό το άρθρο θα συζητήσω εν συντομία την προσέγγισή μου για την κατασκευή του Επίλυσης Τεχνητής Νοημοσύνης του Παιχνιδιού 2048, θα περιγράψω τα ευρετικά που χρησιμοποίησα και θα παράσχω τον πλήρη κώδικα που είναι γραμμένος σε JAVA. Ο κώδικας είναι ανοιχτού κώδικα με άδεια GPL v3 και μπορείτε να τον κατεβάσετε από Github.

Ανάπτυξη του παιχνιδιού 2048 στην JAVA

Το αρχικό παιχνίδι είναι γραμμένο σε JavaScript, οπότε έπρεπε να το ξαναγράψω σε JAVA από την αρχή. Η κύρια ιδέα του παιχνιδιού είναι ότι έχετε ένα πλέγμα 4×4 με ακέραιες τιμές, οι οποίες είναι όλες δυνάμεις του 2. Τα κελιά με μηδενική αξία θεωρούνται άδεια. Σε κάθε σημείο του παιχνιδιού μπορείτε να μετακινήσετε τις τιμές προς 4 κατευθύνσεις Πάνω, Κάτω, Δεξιά ή Αριστερά. Όταν εκτελείτε μια κίνηση, όλες οι τιμές του πλέγματος κινούνται προς αυτήν την κατεύθυνση και σταματούν είτε όταν φτάσουν στα όρια του πλέγματος είτε όταν φτάσουν σε άλλο κελί με μη μηδενική τιμή. Εάν αυτό το προηγούμενο κελί έχει την ίδια τιμή, τα δύο κελιά συγχωνεύονται σε ένα κελί με διπλή τιμή. Στο τέλος κάθε κίνησης προστίθεται μια τυχαία τιμή στον πίνακα σε ένα από τα κενά κελιά και η τιμή της είναι είτε 2 με πιθανότητα 0.9 είτε 4 με 0.1 πιθανότητα. Το παιχνίδι τελειώνει όταν ο παίκτης καταφέρει να δημιουργήσει ένα κελί με τιμή 2048 (νίκη) ή όταν δεν υπάρχουν άλλες κινήσεις να κάνει (ήττα).

Στην αρχική υλοποίηση του παιχνιδιού, ο αλγόριθμος μετακίνησης-συγχώνευσης είναι λίγο περίπλοκος γιατί λαμβάνει υπόψη όλες τις κατευθύνσεις. Μια ωραία απλοποίηση του αλγορίθμου μπορεί να γίνει εάν καθορίσουμε την κατεύθυνση προς την οποία μπορούμε να συνδυάσουμε τα κομμάτια και περιστρέψουμε τον πίνακα ανάλογα για να εκτελέσουμε την κίνηση. Maurits van der Schee έχει γράψει πρόσφατα ένα άρθρο σχετικά με αυτό το οποίο πιστεύω ότι αξίζει να το ελέγξετε.

Όλες οι τάξεις τεκμηριώνονται με σχόλια Javadoc. Παρακάτω παρέχουμε μια περιγραφή υψηλού επιπέδου της αρχιτεκτονικής της υλοποίησης:

1. Τάξη Διοικητικού Συμβουλίου

Η τάξη του πίνακα περιέχει τον κύριο κωδικό του παιχνιδιού, ο οποίος είναι υπεύθυνος για τη μετακίνηση των κομματιών, τον υπολογισμό της βαθμολογίας, την επικύρωση εάν το παιχνίδι τερματίζεται κ.λπ.

2. ActionStatus και Direction Arum

Το ActionStatus και το Direction είναι 2 βασικοί αριθμοί που αποθηκεύουν το αποτέλεσμα μιας κίνησης και την κατεύθυνσή της ανάλογα.

3. ConsoleGame Class

Το ConsoleGame είναι η κύρια κατηγορία που μας επιτρέπει να παίξουμε το παιχνίδι και να δοκιμάσουμε την ακρίβεια του AI Solver.

4. AIsolver Class

Το AIsolver είναι η κύρια κατηγορία της ενότητας Τεχνητής Νοημοσύνης που είναι υπεύθυνη για την αξιολόγηση της επόμενης καλύτερης κίνησης δεδομένου ενός συγκεκριμένου πίνακα.

Τεχνικές Τεχνητής Νοημοσύνης: Κλάδεμα Minimax vs Alpha-beta

Έχουν δημοσιευτεί αρκετές προσεγγίσεις για την αυτόματη επίλυση αυτού του παιχνιδιού. Το πιο αξιοσημείωτο είναι αυτό που αναπτύχθηκε από Ματ Όβερλαν. Για να λύσω το πρόβλημα δοκίμασα δύο διαφορετικές προσεγγίσεις, χρησιμοποιώντας τον αλγόριθμο Minimax και χρησιμοποιώντας το κλάδεμα Alpha-beta.

Αλγόριθμος Minimax

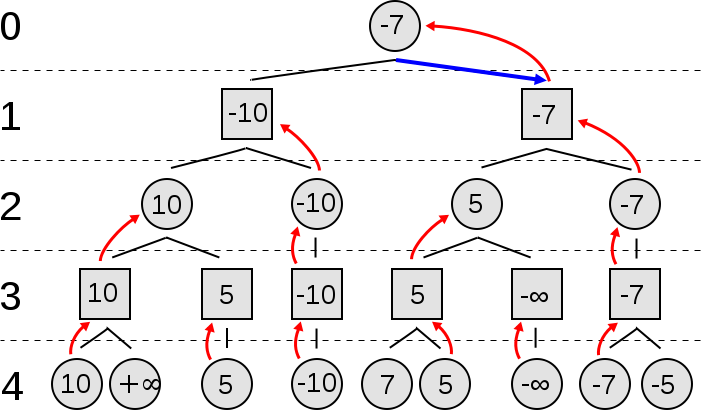
Η Minimax είναι ένας αναδρομικός αλγόριθμος που μπορεί να χρησιμοποιηθεί για την επίλυση παιχνιδιών μηδενικού αθροίσματος δύο παικτών. Σε κάθε κατάσταση του παιχνιδιού συσχετίζουμε μια τιμή. Ο αλγόριθμος Minimax πραγματοποιεί αναζήτηση στο χώρο των πιθανών καταστάσεων παιχνιδιού δημιουργώντας ένα δέντρο το οποίο επεκτείνεται μέχρι να φτάσει σε ένα συγκεκριμένο προκαθορισμένο βάθος. Μόλις επιτευχθούν αυτές οι καταστάσεις φύλλων, οι τιμές τους χρησιμοποιούνται για την εκτίμηση αυτών των ενδιάμεσων κόμβων.

Η ενδιαφέρουσα ιδέα αυτού του αλγορίθμου είναι ότι κάθε επίπεδο αντιπροσωπεύει τη σειρά ενός από τους δύο παίκτες. Για να κερδίσει κάθε παίκτης πρέπει να επιλέξει την κίνηση που ελαχιστοποιεί τη μέγιστη απόδοση του αντιπάλου. Ακολουθεί μια ωραία παρουσίαση βίντεο του αλγόριθμου minimax:

[Ενσωματωμένο περιεχόμενο]

Παρακάτω μπορείτε να δείτε τον ψευδοκώδικα του αλγόριθμου Minimax:

λειτουργία minimax (κόμβος, βάθος, μεγιστοποίηση του προγράμματος αναπαραγωγής)
    if βάθος = 0 or ο κόμβος είναι ένας τερματικός κόμβος
        απόδοση την ευρετική τιμή του κόμβου
    if maximizingPlayer bestValue := -∞
        για κάθε θυγατρικό του κόμβου val := minimax(παιδικό, βάθος - 1, FALSE)) bestValue := max(bestValue, val);
        απόδοση η καλύτερη αξία
    αλλιώς
        bestValue := +∞
        για κάθε θυγατρικό του κόμβου val := ελάχιστη τιμή (παιδί, βάθος - 1, TRUE)) bestValue := min(bestValue, val);
        απόδοση η καλύτερη αξία
(* Αρχική κλήση για μεγιστοποίηση του παίκτη *)
ελάχιστη (προέλευση, βάθος, TRUE)

Αλφα-βήτα κλάδεμα

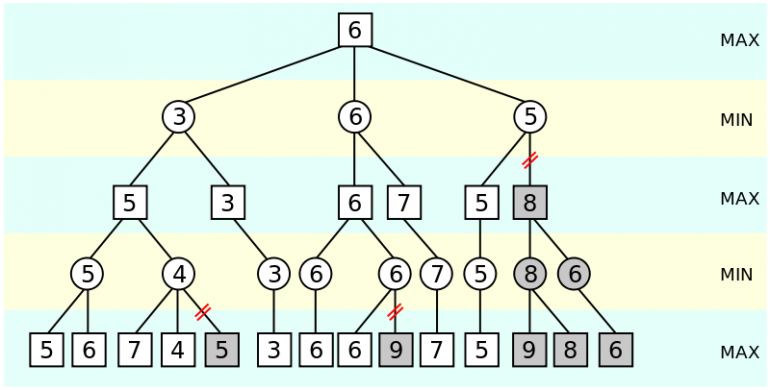
Η Αλγόριθμος κλαδέματος άλφα-βήτα είναι μια επέκταση του minimax, η οποία μειώνει σημαντικά (δαμάσκηνο) τον αριθμό των κόμβων που πρέπει να αξιολογήσουμε/επεκτείνουμε. Για να επιτευχθεί αυτό, ο αλγόριθμος υπολογίζει δύο τιμές το άλφα και το βήτα. Εάν σε έναν δεδομένο κόμβο το βήτα είναι μικρότερο από το άλφα, τότε τα υπόλοιπα υποδέντρα μπορούν να κλαδευτούν. Ακολουθεί μια ωραία παρουσίαση βίντεο του αλφαβήτα αλγορίθμου:

[Ενσωματωμένο περιεχόμενο]

Παρακάτω μπορείτε να δείτε τον ψευδοκώδικα του αλγόριθμου κλαδέματος Alpha-beta:

λειτουργία αλφαβήτα (κόμβος, βάθος, α, β, μεγιστοποίηση αναπαραγωγής)
    if βάθος = 0 or ο κόμβος είναι ένας τερματικός κόμβος
        απόδοση την ευρετική τιμή του κόμβου
    if maximizingPlayer
        για κάθε παιδί του κόμβου α := max(α, αλφαβήτα(παιδί, βάθος - 1, α, β, FALSE))
            if β ≤ α
                σπάσει (* β αποκοπή *)
        απόδοση α
    αλλιώς
        για κάθε παιδί του κόμβου β := min(β, αλφαβήτα(παιδί, βάθος - 1, α, β, TRUE))
            if β ≤ α
                σπάσει (* α αποκοπή *)
        απόδοση β
(* Αρχική κλήση *)
αλφάβητα(προέλευση, βάθος, -∞, +∞, TRUE)

Πώς χρησιμοποιείται η τεχνητή νοημοσύνη για την επίλυση του παιχνιδιού 2048;

Για να χρησιμοποιήσουμε τους παραπάνω αλγόριθμους πρέπει πρώτα να αναγνωρίσουμε τους δύο παίκτες. Ο πρώτος παίκτης είναι το άτομο που παίζει το παιχνίδι. Ο δεύτερος παίκτης είναι ο υπολογιστής που εισάγει τυχαία τιμές στα κελιά του πίνακα. Προφανώς ο πρώτος παίκτης προσπαθεί να μεγιστοποιήσει το σκορ του/της και να πετύχει τη συγχώνευση 2048. Από την άλλη πλευρά, ο υπολογιστής στο αρχικό παιχνίδι δεν είναι ειδικά προγραμματισμένος για να μπλοκάρει τον χρήστη επιλέγοντας τη χειρότερη δυνατή κίνηση για αυτόν, αλλά εισάγει τυχαία τιμές στα κενά κελιά.

Γιατί λοιπόν χρησιμοποιούμε τεχνικές τεχνητής νοημοσύνης που λύνουν παιχνίδια μηδενικού αθροίσματος και που υποθέτουν συγκεκριμένα ότι και οι δύο παίκτες επιλέγουν την καλύτερη δυνατή κίνηση για αυτούς; Η απάντηση είναι απλή. παρά το γεγονός ότι είναι μόνο ο πρώτος παίκτης που προσπαθεί να μεγιστοποιήσει το σκορ του/της, οι επιλογές του υπολογιστή μπορούν να εμποδίσουν την πρόοδο και να εμποδίσουν τον χρήστη να ολοκληρώσει το παιχνίδι. Με τη μοντελοποίηση της συμπεριφοράς του υπολογιστή ως ορθολογικού μη τυχαίου παίκτη, διασφαλίζουμε ότι η επιλογή μας θα είναι σταθερή ανεξάρτητα από αυτό που παίζει ο υπολογιστής.

Το δεύτερο σημαντικό μέρος είναι να εκχωρήσετε τιμές στις καταστάσεις του παιχνιδιού. Αυτό το πρόβλημα είναι σχετικά απλό γιατί το ίδιο το παιχνίδι μας δίνει βαθμολογία. Δυστυχώς το να προσπαθείς να μεγιστοποιήσεις το σκορ από μόνη της δεν είναι καλή προσέγγιση. Ένας λόγος για αυτό είναι ότι η θέση των τιμών και ο αριθμός των κενών κελιών είναι πολύ σημαντικά για να κερδίσετε το παιχνίδι. Για παράδειγμα, εάν διασκορπίσουμε τις μεγάλες τιμές σε απομακρυσμένα κελιά, θα ήταν πραγματικά δύσκολο για εμάς να τις συνδυάσουμε. Επιπλέον, εάν δεν έχουμε κενά διαθέσιμα, κινδυνεύουμε να χάσουμε το παιχνίδι ανά πάσα στιγμή.

Για όλους τους παραπάνω λόγους, αρκετά ευρετικά έχουν προταθεί όπως το Monoticity, η ομαλότητα και τα Free Tiles του ταμπλό. Η κύρια ιδέα δεν είναι να χρησιμοποιήσετε μόνο το σκορ για την αξιολόγηση κάθε κατάστασης παιχνιδιού, αλλά να δημιουργήσετε μια ευρετική σύνθετη βαθμολογία που περιλαμβάνει τις προαναφερθείσες βαθμολογίες.

Τέλος, θα πρέπει να σημειώσουμε ότι παρόλο που έχω αναπτύξει μια υλοποίηση του αλγορίθμου Minimax, ο μεγάλος αριθμός πιθανών καταστάσεων καθιστά τον αλγόριθμο πολύ αργό και επομένως το κλάδεμα είναι απαραίτητο. Ως αποτέλεσμα στην υλοποίηση JAVA χρησιμοποιώ την επέκταση του αλγορίθμου κλαδέματος Alpha-beta. Επιπλέον, σε αντίθεση με άλλες υλοποιήσεις, δεν κλαδεύω επιθετικά τις επιλογές του υπολογιστή χρησιμοποιώντας αυθαίρετους κανόνες, αλλά αντίθετα τις λαμβάνω όλες υπόψη για να βρω την καλύτερη δυνατή κίνηση του παίκτη.

Ανάπτυξη μιας ευρετικής συνάρτησης βαθμολογίας

Για να κερδίσω το παιχνίδι, δοκίμασα πολλές διαφορετικές ευρετικές λειτουργίες. Αυτό που βρήκα πιο χρήσιμο είναι το εξής:

private static int heuristicScore(int actualScore, int numberOfEmptyCells, int clusteringScore) {
     int score = (int) (actualScore+Math.log(actualScore)*numberOfEmptyCells -clusteringScore);
     return Math.max(score, Math.min(actualScore, 1));
}

Η παραπάνω συνάρτηση συνδυάζει την πραγματική βαθμολογία του πίνακα, τον αριθμό των κενών κελιών/πλακιδίων και μια μέτρηση που ονομάζεται βαθμολογία ομαδοποίησης, την οποία θα συζητήσουμε αργότερα. Ας δούμε κάθε στοιχείο με περισσότερες λεπτομέρειες:

1. Πραγματική βαθμολογία: Για ευνόητους λόγους, όταν υπολογίζουμε την αξία ενός πίνακα πρέπει να λαμβάνουμε υπόψη και τη βαθμολογία του. Οι πίνακες με υψηλότερες βαθμολογίες προτιμώνται γενικά σε σύγκριση με πίνακες με χαμηλότερες βαθμολογίες.
2. Αριθμός κενών κελιών: Όπως αναφέραμε προηγουμένως, το να διατηρούμε λίγα κενά κελιά είναι σημαντικό για να διασφαλίσουμε ότι δεν θα χάσουμε το παιχνίδι στις επόμενες κινήσεις. Οι καταστάσεις πίνακα με περισσότερα κενά κελιά προτιμώνται γενικά σε σύγκριση με άλλες με λιγότερα. Εγείρεται ένα ερώτημα σχετικά με το πώς θα εκτιμούσαμε αυτά τα άδεια κελιά; Στη λύση μου τα ζυγίζω με τον λογάριθμο της πραγματικής βαθμολογίας. Αυτό έχει το εξής αποτέλεσμα: Όσο χαμηλότερη είναι η βαθμολογία, τόσο λιγότερο σημαντικό είναι να υπάρχουν πολλά άδεια κελιά (Αυτό συμβαίνει επειδή στην αρχή του παιχνιδιού ο συνδυασμός των κελιών είναι αρκετά εύκολος). Όσο υψηλότερο είναι το σκορ, τόσο πιο σημαντικό είναι να διασφαλίσουμε ότι θα έχουμε άδεια κελιά στο παιχνίδι μας (Αυτό συμβαίνει γιατί στο τέλος του παιχνιδιού είναι πιο πιθανό να χάσουμε λόγω έλλειψης κενών κελιών.
3. Βαθμολογία ομαδοποίησης: Χρησιμοποιούμε τη βαθμολογία ομαδοποίησης που μετρά πόσο διάσπαρτες είναι οι τιμές του πίνακα μας. Όταν τα κελιά με παρόμοιες τιμές είναι κοντά, είναι πιο εύκολο να συνδυαστούν, πράγμα που σημαίνει ότι είναι πιο δύσκολο να χάσεις το παιχνίδι. Σε αυτή την περίπτωση η βαθμολογία ομαδοποίησης έχει χαμηλή τιμή. Εάν οι τιμές του πίνακα είναι διάσπαρτες, τότε αυτή η βαθμολογία παίρνει πολύ μεγάλη τιμή. Αυτή η βαθμολογία αφαιρείται από τις δύο προηγούμενες βαθμολογίες και λειτουργεί σαν πέναλτι που διασφαλίζει ότι θα προτιμηθούν οι πίνακες σε ομάδες.

Στην τελευταία γραμμή της συνάρτησης διασφαλίζουμε ότι η βαθμολογία είναι μη αρνητική. Η βαθμολογία πρέπει να είναι αυστηρά θετική εάν η βαθμολογία του πίνακα είναι θετική και μηδενική μόνο όταν η βαθμολογία της βαθμολογίας είναι μηδέν. Οι συναρτήσεις max και min είναι κατασκευασμένες έτσι ώστε να έχουμε αυτό το εφέ.

Τέλος, θα πρέπει να σημειώσουμε ότι όταν ο παίκτης φτάσει σε κατάσταση τερματικού παιχνιδιού και δεν επιτρέπονται άλλες κινήσεις, δεν χρησιμοποιούμε την παραπάνω βαθμολογία για να εκτιμήσουμε την αξία της κατάστασης. Εάν το παιχνίδι κερδηθεί, εκχωρούμε την υψηλότερη δυνατή ακέραια τιμή, ενώ αν το παιχνίδι χαθεί εκχωρούμε τη χαμηλότερη μη αρνητική τιμή (0 ή 1 με παρόμοια λογική όπως στην προηγούμενη παράγραφο).

Περισσότερα για τη βαθμολογία ομαδοποίησης

Όπως είπαμε νωρίτερα, η βαθμολογία ομαδοποίησης μετρά πόσο διάσπαρτες είναι οι τιμές του ταμπλό και λειτουργεί σαν πέναλτι. Κατασκεύασα αυτό το σκορ με τέτοιο τρόπο ώστε να ενσωματώνει συμβουλές/κανόνες από χρήστες που «κατακτούσαν» το παιχνίδι. Ο πρώτος προτεινόμενος κανόνας είναι ότι προσπαθείτε να κρατήσετε κοντά τα κελιά με παρόμοιες τιμές για να τα συνδυάσετε ευκολότερα. Ο δεύτερος κανόνας είναι ότι τα κελιά υψηλής αξίας πρέπει να βρίσκονται το ένα κοντά στο άλλο και να μην εμφανίζονται στη μέση του πίνακα, αλλά στις πλευρές ή στις γωνίες.

Ας δούμε πώς υπολογίζεται η βαθμολογία ομαδοποίησης. Για κάθε κελί του πίνακα υπολογίζουμε το άθροισμα των απόλυτων διαφορών από τους γείτονές του (εξαιρουμένων των κενών κελιών) και παίρνουμε τη μέση διαφορά. Ο λόγος για τον οποίο παίρνουμε τους μέσους όρους είναι για να αποφύγουμε να μετρήσουμε περισσότερες από μία φορές την επίδραση δύο γειτονικών κελιών. Η συνολική βαθμολογία ομαδοποίησης είναι το άθροισμα όλων αυτών των μέσων όρων.

Η βαθμολογία ομαδοποίησης έχει τα ακόλουθα χαρακτηριστικά:

1. Παίρνει υψηλή τιμή όταν οι τιμές του πίνακα είναι διάσπαρτες και χαμηλή τιμή όταν κελιά με παρόμοιες τιμές είναι κοντά το ένα στο άλλο.
2. Δεν υπερβαραίνει την επίδραση δύο γειτονικών κυττάρων.
3. Τα κελιά στα περιθώρια ή τις γωνίες έχουν λιγότερους γείτονες και επομένως χαμηλότερες βαθμολογίες. Ως αποτέλεσμα όταν οι υψηλές τιμές τοποθετούνται κοντά στα περιθώρια ή τις γωνίες έχουν μικρότερο σκορ και έτσι η ποινή είναι μικρότερη.

Η ακρίβεια του αλγορίθμου

Όπως ήταν αναμενόμενο, η ακρίβεια (γνωστός και ως το ποσοστό των παιχνιδιών που κερδίζονται) του αλγορίθμου εξαρτάται σε μεγάλο βαθμό από το βάθος αναζήτησης που χρησιμοποιούμε. Όσο μεγαλύτερο είναι το βάθος της αναζήτησης, τόσο μεγαλύτερη είναι η ακρίβεια και τόσο περισσότερος χρόνος απαιτείται για να εκτελεστεί. Στις δοκιμές μου, μια αναζήτηση με βάθος 3 διαρκεί λιγότερο από 0.05 δευτερόλεπτα, αλλά δίνει 20% πιθανότητα νίκης, ένα βάθος 5 διαρκεί περίπου 1 δευτερόλεπτο, αλλά δίνει 40% πιθανότητα νίκης και, τέλος, ένα βάθος 7 διαρκεί 27-28 δευτερόλεπτα και δίνει περίπου 70-80% πιθανότητες νίκης.

Μελλοντικές επεκτάσεις

Για όσους από εσάς ενδιαφέρεστε να βελτιώσετε τον κώδικα, υπάρχουν μερικά πράγματα που μπορείτε να εξετάσετε:

1. Βελτιώστε την ταχύτητα: Η βελτίωση της ταχύτητας του αλγορίθμου θα σας επιτρέψει να χρησιμοποιήσετε μεγαλύτερο βάθος και έτσι να έχετε καλύτερη ακρίβεια.
2. Δημιουργία γραφικών: Υπάρχει ένας καλός λόγος για τον οποίο η εφαρμογή του Gabriele Cirulli έγινε τόσο διάσημη. Έχει ωραία εμφάνιση! Δεν μπήκα στον κόπο να αναπτύξω ένα γραφικό περιβάλλον, αλλά μάλλον εκτυπώνω τα αποτελέσματα στην κονσόλα, κάτι που κάνει το παιχνίδι πιο δύσκολο στην παρακολούθηση και την αναπαραγωγή. Η δημιουργία ενός ωραίου GUI είναι απαραίτητη.
3. Συντονισμός Ευρετικών: Όπως ανέφερα προηγουμένως, αρκετοί χρήστες έχουν προτείνει διαφορετικά ευρετικά. Μπορεί κανείς να πειραματιστεί με τον τρόπο που υπολογίζονται οι βαθμολογίες, τα βάρη και τα χαρακτηριστικά του πίνακα που λαμβάνονται υπόψη. Η προσέγγισή μου για τη μέτρηση της βαθμολογίας του συμπλέγματος υποτίθεται ότι συνδυάζει άλλες προτάσεις όπως Μονοτονία και Ομαλή, αλλά υπάρχει ακόμα περιθώριο βελτίωσης.
4. Ρύθμιση του βάθους: Κάποιος μπορεί επίσης να προσπαθήσει να συντονίσει/προσαρμόσει το βάθος της αναζήτησης ανάλογα με την κατάσταση του παιχνιδιού. Επίσης μπορείτε να χρησιμοποιήσετε το Επαναληπτική αναζήτηση βάθους εμβάθυνσης αλγόριθμος που είναι γνωστό ότι βελτιώνει τον αλγόριθμο κλαδέματος άλφα-βήτα.

Μην ξεχάσετε να κατεβάσετε τον κώδικα JAVA από Github και πειραματιστείτε. Ελπίζω να σας άρεσε αυτή η ανάρτηση! Εάν το κάνατε, αφιερώστε λίγο χρόνο για να μοιραστείτε το άρθρο στο Facebook και στο Twitter. 🙂