Sorprendente prueba informática sorprende a los matemáticos

El domingo 5 de febrero, Olof Sisask y Thomas Bloom recibieron un correo electrónico que contenía un sorprendente avance sobre el mayor problema sin resolver en su campo. Zander Kelley, un estudiante graduado de la Universidad de Illinois, Urbana-Champaign, había enviado a Sisask y Bloom un papel que había escrito con Raghu Meka de la Universidad de California, Los Ángeles. Tanto Kelley como Meka eran informáticos, un mundo intelectual aparte de la combinatoria aditiva que estudian Sisask y Bloom.

“Mi mente estaba simplemente volada. Como, espera, ¿realmente han hecho esto? dijo Sisask, profesor de la Universidad de Estocolmo. Kelley y Meka, expertos en el campo de la combinatoria, dijeron que habían encontrado un límite nuevo, y mucho más bajo, en el tamaño de un conjunto de números enteros en el que tres de ellos no están espaciados uniformemente (descartando combinaciones como 3, 8 y 13). o 101, 201 y 301).

El reclamo de Kelley y Meka rompió el récord anterior, alcanzado en 2020 por Sisask y Bloom, quien es investigador en la Universidad de Oxford. “El trabajo de Bloom y Sisask, un trabajo muy sólido, realmente dio la impresión de ser súper difícil de mejorar”, dijo Ben Green, un colega de Bloom en Oxford. “Parecía muy atascado en donde estaba”.

Aunque tanto Bloom como Sisask tenían otros asuntos urgentes que atender en el momento en que recibieron el correo electrónico (Bloom acababa de adoptar un cachorro, mientras que Sisask estaba a punto de mudarse), rápidamente se pusieron a trabajar para verificar el nuevo documento.

En cuestión de días, Bloom y Sisask estaban convencidos de que la nueva prueba era correcta. Sisask lo llamó “el mayor resultado en el área en 20 años”. Deseosos de que otros apreciaran las ideas de Kelley y Meka, redactaron para informar explicando la prueba en términos más familiares para los matemáticos.

Meka dijo que la respuesta de la comunidad “ha sido más positiva de lo que pensaba. Es increíble ver todos los comentarios”.

Progreso prolongado

Las secuencias de números espaciados uniformemente que Kelley y Meka intentaron evitar se denominan progresiones aritméticas. Pueden continuar para siempre o contener solo unos pocos términos. Kelley y Meka se centraron en progresiones compuestas de solo tres números, siguiendo una línea de investigación que a menudo se remonta a un papel 1936 de Paul Erdős y Paul Turán.

Erdős y Turán querían saber cuántos números más pequeños que un techo N se puede poner en un conjunto sin crear progresiones aritméticas de tres términos. N podría ser 1,000, 1 millón o algún número inimaginablemente grande. Ellos conjeturaron que como N creció, un conjunto sin progresiones de tres términos tendría que volverse increíblemente escaso. Crear un conjunto de este tipo sería como coleccionar zapatos insistiendo en que no hay dos pares del mismo color. Tal vez podría continuar para siempre, pero a medida que su colección creciera, se encontraría agregando más a un ritmo cada vez más lento.

“Hay cierta estructura que aparecerá en el set, sin importar cómo lo elijas”, explicó Meka. "¿Qué tan grande es el conjunto que realmente necesita para garantizar que tiene esta estructura allí?"

En 1946, Félix Behrend encontró una manera de construir conjuntos de números entre 1 y N sin producir progresiones de tres términos. Su método dio como resultado conjuntos que se hicieron más grandes a medida que N Lo hizo, pero dolorosamente lento. Cuando N es 100,000, el conjunto de Behrend contiene solo 171 elementos. Cuando N es 1 millón, su conjunto tiene 586 números, menos del 0.06% de los números entre 1 y 1 millón.

Los conjuntos de Behrend dieron a los matemáticos un piso con el que trabajar: el conjunto más grande sin una progresión de tres términos tendría que ser al menos tan grande como el de Behrend. En 1953, Klaus Roth proporcionado un techo, encontrando un umbral más allá del cual un conjunto debe contener inevitablemente una progresión de tres términos.

Roth había probado la conjetura de Erdős y Turán mostrando que como N crece, un conjunto sin progresiones de tres términos comprenderá una fracción cada vez más pequeña de los números entre 1 y N. Pero el techo de Roth estaba muy lejos del piso de Behrend. Behrend había demostrado que el 0.06% de los elementos entre 1 y 1 millón podrían caber dentro de un conjunto sin progresión. Aunque la fórmula de Roth es difícil de calcular con precisión, no está ni cerca de ser tan baja: una estimación aproximada indica que limita el porcentaje en alrededor del 40 %.

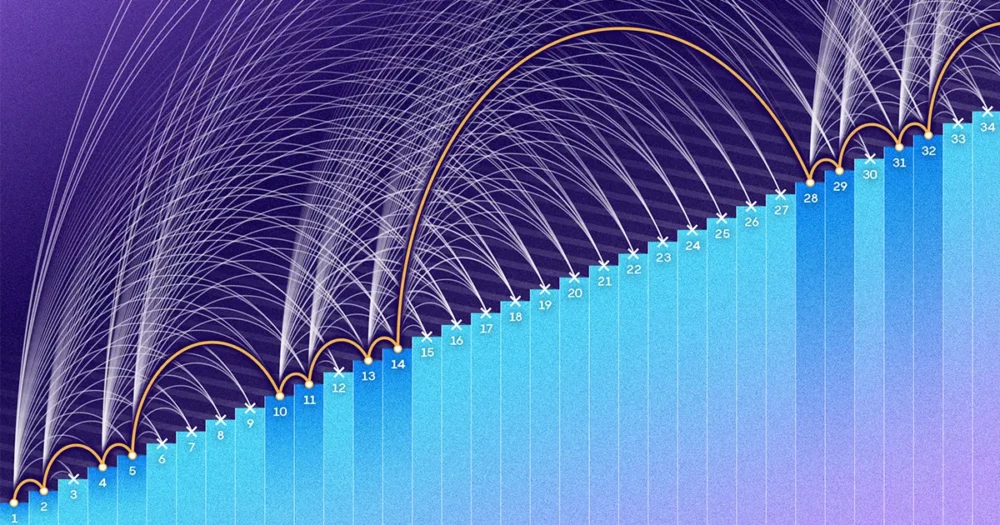
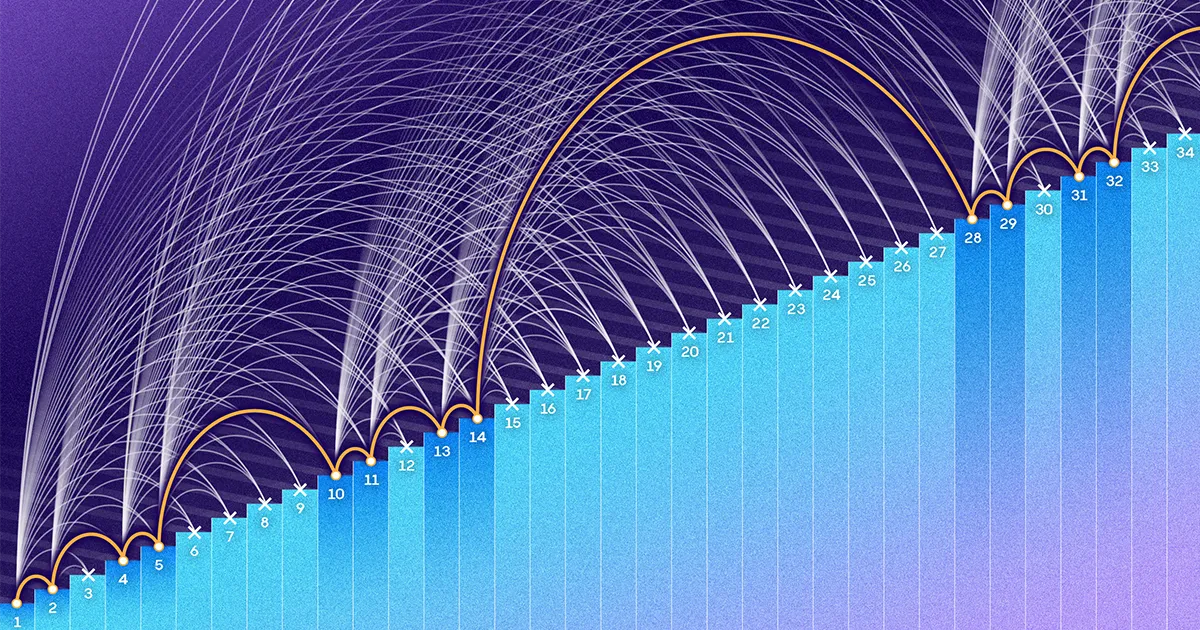
Pero más destacado que esa brecha en particular fue el comportamiento general de las dos fórmulas. Grafica la fracción de elementos entre 1 y N que representa cada fórmula, y verá que el número de Behrend se reduce rápidamente a cero como N crece La fracción de Roth, por otro lado, se desliza hacia cero, pero lenta y suavemente. Las dos curvas tienen formas muy diferentes, y la verdadera proporción de elementos que se encuentran en un conjunto sin progresiones aritméticas podría, hasta donde sabían los matemáticos, estar en cualquier lugar entre ellas.

A partir de la década de 1980, "hubo una larga secuencia de, en retrospectiva, mejoras bastante incrementales por parte de un gran número de matemáticos realmente famosos", dijo Green. De vez en cuando, alguien bajaba uno o dos cabellos el límite superior de Roth y, finalmente, se reducía considerablemente. El límite inferior de Behrend, por el contrario, no se movió durante décadas. Los matemáticos comenzaron a pensar que Behrend podría no haber estado lejos de la verdadera respuesta, dijo Bloom.

Hasta que llegó el artículo de Kelley y Meka a principios de 2023, el tamaño máximo de un conjunto sin progresión estaba definido desde abajo por la fórmula de Behrend, y desde arriba por la de Bloom y Sisask. El artículo de Bloom y Sisask de julio de 2020 había cruzado el umbral "logarítmico" crítico al mostrar que un conjunto sin progresión debe tener sustancialmente menos de N/(registro N) elementos. Pero su resultado aún estaba muy por encima del de Behrend. El nuevo límite superior de Kelley y Meka está drásticamente más cerca del piso establecido por Behrend.

“Meka y Kelley han superado todo este progreso gradual”, dijo Terence Tao, un destacado matemático de la UCLA.

Su fórmula es casi la misma que la de Behrend, con solo unos pocos parámetros modificados. Como N se aproxima al infinito, un gráfico de la fórmula de Kelley y Meka finalmente se asentará en una curva que se parece a la curva de Behrend. “Cualquier límite de esa forma parecía un sueño imposible antes”, dijo Bloom.

“Realmente estaba bastante asombrado de que hubieran hecho tal mejora”, dijo Green.

Una táctica diferente

 Aunque Kelley y Meka nunca antes se habían aventurado por completo en la investigación matemática pura, las progresiones aritméticas les eran familiares cuando comenzaron. En general, los científicos informáticos “buscan ávidamente técnicas que funcionen para resolver nuestros problemas”, dijo Kelley. Las herramientas utilizadas históricamente para estudiar el tamaño de un conjunto libre de progresión se han vuelto ampliamente utilizadas en el subcampo de informática de la teoría de la complejidad. El problema de reducir el tamaño de un conjunto de este tipo es bien conocido por los teóricos de la complejidad como un ejemplo por excelencia de la aplicación de técnicas que prueban la estructura interna de los conjuntos.

A fines de 2021, Kelley y Meka estaban analizando las posibilidades de que un equipo de jugadores en cierto juego cooperativo pudiera ganar, un tipo estándar de problema informático. Se les ocurrió que las técnicas de investigación sobre el tamaño de las series sin progresión podrían ser útiles. Pero les resultó más fácil estudiar directamente esas técnicas que aplicarlas al juego cooperativo. “Mi mejor idea sobre cómo avanzar en este problema [fue] mejorar la herramienta en sí, no usarla de una manera más inteligente”, dijo Kelley.

“En algún momento, simplemente decidimos trabajar en esta pregunta directamente”, recordó Meka. Seis meses después, los dos investigadores habían descubierto su estrategia y solo necesitaban resolver cómo aplicar su método al problema en cuestión.

Para ver cómo llegaron a su nuevo límite superior, tome cualquier conjunto de números entre 1 y N. Llámalo A. La densidad de A es el porcentaje de los números entre 1 y N que incluye. Como hay muchas progresiones aritméticas posibles entre 1 y N, si no elige los elementos de A con cuidado, cualquier A con alta densidad probablemente contendrá muchas progresiones aritméticas.

En su demostración, Kelley y Meka imaginaron que A tenían pocas progresiones aritméticas o ninguna, e intentaron rastrear las consecuencias. Si A era lo suficientemente denso, mostraron que la ausencia de progresiones requería un nivel de estructura dentro A eso inevitablemente resultaría en una contradicción, lo que significa que A debe, después de todo, contener al menos una progresión.

Para entender esa estructura, consideraron el conjunto A + A, que consta de todos los números formados al sumar dos elementos de A. Se dieron cuenta de que si A contiene comparativamente pocas progresiones aritméticas, esto implica una redundancia entre los elementos de A + A: Diferentes pares de números de A a menudo suman el mismo número.

La densidad se puede definir no solo en comparación con todos los números enteros entre 1 y N pero en comparación con algún subconjunto, digamos solo los números pares en ese intervalo, o solo los múltiplos de 3. Kelley y Meka usaron las redundancias en A + A para encontrar un subconjunto de los enteros donde los elementos de A eran particularmente comunes.

Si A contenía desproporcionadamente muchos múltiplos de 3, por ejemplo, Kelley y Meka se enfocarían en la parte que incluía múltiplos de 3. Repitieron esta estrategia una y otra vez. Cada vez encontraron subconjuntos cada vez más pequeños de los números enteros, sobre los cuales ALa densidad de 's seguiría creciendo y creciendo. Por ejemplo, A podría contener el 10% de los números enteros entre 1 y N, 15% de los múltiplos de 3 en ese intervalo, y 25% de los múltiplos pares de 3.

Algo interesante sucede cuando A es largo. Si se repite el procedimiento, la densidad de A sobre algún subconjunto excede el 100%. Eso, por supuesto, es imposible. A podría contener, digamos, todos los múltiplos de 24, pero no puede contener más que todos ellos. Esta paradoja sólo surge si A es lo suficientemente grande para empezar, pero cuando lo hace, significa la suposición de que A no contiene progresiones aritméticas debe haber estado mal.

Es un "argumento de ganar-ganar", cuando A es grande, dijo Meka. Cualquiera A incluye muchas progresiones aritméticas, o hay mucha redundancia en A + A — en cuyo caso podrían usar el procedimiento de búsqueda de subconjuntos (llamado "estrategia de incremento de densidad") para mostrar que una progresión debe aparecer en A. Si bien la estrategia de incremento de densidad es un modelo bien usado en el campo, Kelley y Meka lograron que funcionara para empresas más pequeñas. A's que nunca antes. Con eso, descubrieron un nuevo techo para el tamaño de un set sin progresión.

Kelley y Meka crearon una combinación única de ideas a partir del modelo de incremento de densidad. En lugar de crear un marco completamente nuevo, repensaron la forma en que encontraron su subconjunto denso. Para ello, utilizaron una técnica que llamaron “tamizado”, que consiste en desplazar su conjunto en una cantidad constante, cruzarlo consigo mismo y repetir el proceso muchas, muchas veces. Lo que queda, después de muchas rondas de intersección, es un conjunto altamente estructurado con propiedades predecibles. Aunque el tamizado se ha utilizado en otros artículos, nunca se había probado en el problema de progresión de tres términos.

Mirando hacia atrás

Kelley y Meka redujeron el límite de tamaño de un conjunto sin progresión en una cantidad sorprendente al inyectar herramientas olvidadas como tamizar en métodos tradicionales. “Kelley y Meka nos han demostrado que, de alguna manera, estas técnicas, que estaban expuestas, eran mucho más poderosas de lo que sospechábamos”, dijo Bloom. A la luz de la eficacia recién descubierta de estas herramientas, agregó, “tenemos que regresar y revisar todo”.

La estrategia de incremento de densidad apareció por primera vez en el artículo de Roth hace 70 años y desde entonces se ha utilizado en la mayoría de los artículos sobre progresiones aritméticas. Green se sorprendió de que el marco pudiera usarse para probar un límite tan bajo como el de Kelley y Meka. “Pensé que se necesitaría algo completamente, radicalmente diferente”, dijo.

Kelley está emocionado de continuar su incursión en las matemáticas. “No me faltan esperanzas y sueños sobre muchos problemas diferentes que consideraría al menos espiritualmente relacionados con esto”, dijo.

Que Kelley y Meka lograran detectar la fuerza de ideas que antes se pasaban por alto muestra la naturaleza a menudo irregular del progreso matemático, una cualidad que para Tao es más una bendición que una maldición. “No siempre es el caso de que las matemáticas se vuelvan cada vez más y más difíciles”, dijo. "Gracias a Dios."