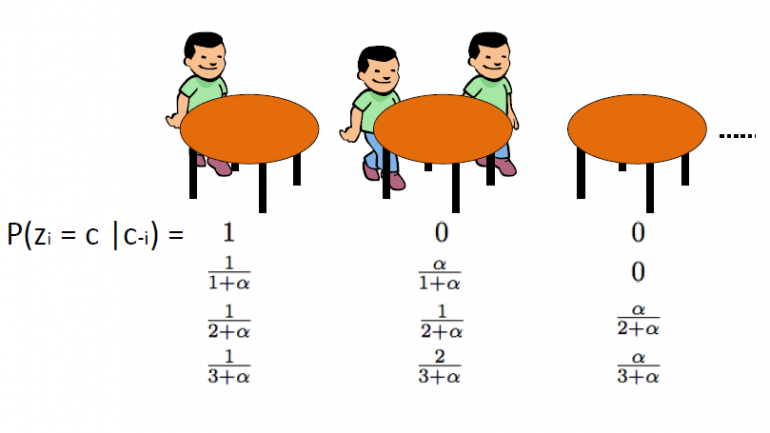El proceso de Dirichlet El proceso del restaurante chino y otras representaciones

• 20 de mayo de 2014
• Vasilis Vryniotis
• . Sin comentarios

Este artículo es la tercera parte de la serie sobre Agrupación con modelos de mezcla de procesos de Dirichlet. La vez anterior definimos el modelo de mezcla finita basado en la distribución de Dirichlet y planteamos preguntas sobre cómo podemos hacer que este modelo en particular sea infinito. Discutimos brevemente la idea de tomar el límite del modelo cuando el número k de grupos tiende a infinito, pero como enfatizamos, la existencia de tal objeto no es trivial (en otras palabras, ¿cómo podemos realmente “tomar el límite de un modelo ”?). Como recordatorio, la razón por la que queremos tomar make k infinite es porque de esta manera tendremos un modelo no paramétrico que no nos obliga a predefinir el número total de clusters dentro de los datos.

Actualización: el marco de aprendizaje automático de Datumbox ahora es de código abierto y gratuito para descargar. Consulte el paquete com.datumbox.framework.machinelearning.clustering para ver la implementación de los modelos de mezcla de procesos de Dirichlet en Java.

Aunque nuestro objetivo es construir un modelo que sea capaz de realizar agrupaciones en conjuntos de datos, antes de eso debemos discutir sobre los procesos de Dirichlet. Proporcionaremos tanto las definiciones matemáticas estrictas como las explicaciones más intuitivas de DP y discutiremos formas de construir el proceso. Esas construcciones / representaciones pueden verse como una forma de encontrar ocurrencias del Proceso de Dirichlet en la “vida real”.

A pesar de que intenté adaptar mi informe de investigación de tal manera que estas publicaciones de blog sean más fáciles de seguir, sigue siendo importante definir las herramientas matemáticas y las distribuciones necesarias antes de comenzar a usar los modelos. Los modelos de procesos de Dirichlet son un tema de investigación activa, pero requieren tener una buena comprensión de la estadística y los procesos estocásticos antes de usarlos. Otro problema es que, como veremos en este artículo, los procesos de Dirichlet se pueden representar / construir de numerosas formas. Como resultado, varios artículos académicos utilizan notación / convenciones completamente diferentes y examinan el problema desde diferentes puntos de vista. En esta publicación trato de explicarlos de la manera más simple posible y usar la misma notación. Con suerte, las cosas se aclararán con los dos próximos artículos que se centran en la definición de los modelos de mezcla de procesos de Dirichlet y en cómo utilizarlos para realizar análisis de conglomerados.

1. Definición del proceso de Dirichlet

Un proceso de Dirichlet sobre un espacio Θ es un proceso estocástico. Es una distribución de probabilidad sobre "distribuciones de probabilidad sobre Θ espacio" y una extraer de él es una distribución discreta. Más formalmente, una distribución de Dirichlet es una distribución sobre medidas de probabilidad. UN medida de probabilidad es una función de subconjuntos del espacio Θ a [0,1]. G es una medida de probabilidad aleatoria distribuida por DP, denotada como , si para cualquier partición (A₁,…UN_n) de espacio Θ tenemos eso .

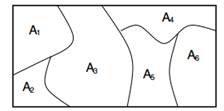
Figura 1: Los marginales en particiones finitas se distribuyen en Dirichlet.

El DP tiene dos parámetros: el primero es la distribución base G₀ que sirve como un medio . El segundo es el parámetro de fuerza α que es estrictamente positivo y sirve como varianza inversa . Determina el grado de repetición de los valores de la distribución de salida. Cuanto mayor sea el valor de a, menor será la repetición; cuanto menor sea el valor, mayor será la repetición de los valores de distribución de la producción. Finalmente, el espacio Θ es el espacio de parámetros en el que definimos el DP. Además, el espacio Θ es también el espacio de definición de G₀ que es el mismo que el de G.

Un mas simple y mas forma intuitiva para explicar un proceso de Dirichlet es lo siguiente. Supongamos que tenemos un espacio Θ que se puede dividir de cualquier manera finita (A₁,…,UN_n) y una distribución de probabilidad G que les asigna probabilidades. La G es una distribución de probabilidad específica sobre Θ, pero hay muchas otras. El Proceso de Dirichlet en Θ modela exactamente esto; es una distribución sobre todas las posibles distribuciones de probabilidad en el espacio Θ. El proceso de Dirichlet se parametriza con el G₀ función de base y el parámetro de concentración α. Podemos decir que G se distribuye según DP con parámetros α y G₀ si la distribución conjunta de las probabilidades que G asigna a las particiones de Θ sigue la Distribución de Dirichlet. Alternativamente, podemos decir que las probabilidades que G asigna a cualquier partición finita de Θ sigue la Distribución de Dirichlet.

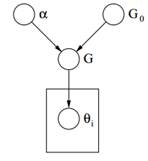
Figura 2: Modelo gráfico del proceso de Dirichlet

Finalmente arriba podemos ver el modelo gráfico de un DP. Debemos tener en cuenta que α es un hiperparámetro escalar, G₀ es la distribución base de DP, G una distribución aleatoria sobre Θ espacio de parámetros muestreado del DP que asigna probabilidades a los parámetros y θ_i es un vector de parámetro que se extrae de la distribución G y es un elemento del espacio Θ.

2. Procesos de Dirichlet posteriores

Los procesos de Dirichlet posteriores fueron discutidos por Ferguson. Comenzamos dibujando una medida de probabilidad aleatoria G de un proceso de Dirichlet, . Dado que G es una distribución de probabilidad sobre Θ, también podemos tomar muestras de esta distribución y extraer muestras independientes distribuidas de manera idéntica θ₁,…, Θ_n ~ G. Dado que las extracciones de un proceso de Dirichlet son distribuciones discretas, podemos representar donde es una notación corta para que es una función delta que toma 1 si y 0 en otros lugares. Un efecto interesante de esto es que dado que G se define de esta manera, existe una probabilidad positiva de que diferentes muestras tengan el mismo valor. . Como veremos más adelante, esto crea un efecto de agrupamiento que se puede utilizar para realizar análisis de conglomerados en conjuntos de datos.

Mediante el uso de las definiciones y observaciones anteriores, queremos estimar el posterior del Proceso de Dirichlet dadas las muestras θ. Sin embargo, ya que sabemos que y al usar las Reglas de Bayes y el Conjugado entre Dirichlet y Multinomial tenemos que y .

Ecuación 1: Proceso de Dirichlet posterior

Esta propiedad es muy importante y la utilizan las diversas representaciones de DP.

3. Representaciones del proceso de Dirichlet

En los segmentos anteriores definimos el Proceso de Dirichlet y presentamos su modelo teórico. Una pregunta importante que debemos responder es cómo sabemos que tal objeto existe y cómo podemos construir y representar un proceso de Dirichlet.

Los primeros indicios de existencia fueron proporcionados por Ferguson que utilizó el teorema de coherencia de Kolmogorov, dio la definición de un proceso de Dirichlet y describió el proceso de Dirichlet posterior. Continuando con su investigación, Blackwell y MacQueen usó el teorema de de Finetti para probar la existencia de tal medida de probabilidad aleatoria e introdujo el esquema de urn Blackwell-MacQueen que satisface las propiedades del proceso de Dirichlet. En 1994 Sethuraman proporcionó una forma adicional simple y directa de construir un DP al introducir la construcción Stick -break. Finalmente otra representación fue proporcionada por Aldous quien introdujo el Proceso de Restaurante Chino como una forma efectiva de construir un Proceso de Dirichlet.

Las diversas Representaciones del Proceso de Dirichlet son matemáticamente equivalentes pero su formulación difiere porque examinan el problema desde diferentes puntos de vista. A continuación, presentamos las representaciones más comunes encontradas en la literatura y nos enfocamos en el proceso de restaurante chino, que proporciona una forma simple y computacionalmente eficiente para construir algoritmos de inferencia para el proceso de Dirichlet.

3.1 El esquema de urnas de Blackwell-MacQueen

El esquema de urnas Blackwell-MacQueen se puede utilizar para representar un proceso de Dirichlet y fue introducido por Blackwell y MacQueen. Se basa en el esquema de urnas de Pólya, que puede verse como el modelo opuesto de muestreo sin reemplazo. En el esquema de la urna de Pólya asumimos que tenemos una urna no transparente que contiene bolas de colores y las extraemos al azar. Cuando sacamos una bola, observamos su color, la volvemos a meter en la urna y le añadimos una bola adicional del mismo color. Blackwell y MacQueen utilizan un esquema similar para construir un proceso de Dirichlet.

Este esquema produce una secuencia de θ₁, θ₂,… con probabilidades condicionales . En este esquema asumimos que G₀ es una distribución sobre colores y cada θ_n representa el color de la bola que se coloca en la urna. los algoritmo es el siguiente:

· Empezamos con una urna vacía.

· Con probabilidad proporcional a α nosotros dibujamos y añadimos una bola de este color en la urna.

· Con probabilidad proporcional a n-1 sacamos una bola aleatoria de la urna, observamos su color, la volvemos a colocar en la urna y añadimos una bola adicional del mismo color en la urna.

Anteriormente, comenzamos con un proceso de Dirichlet y derivamos el esquema Blackwell-MacQueen. Ahora comencemos a la inversa del esquema Blackwell-MacQueen y derivemos el DP. Desde θ_i fueron extraídas de una manera iid de G, su distribución conjunta será invariante a cualquier permutaciones finitas y por lo tanto son intercambiables. En consecuencia, al usar el teorema de De Finetti, tenemos que debe existir una distribución sobre las medidas para hacerlas iid y esta distribución es el Proceso de Dirichlet. Como resultado, probamos que el esquema de urna de Blackwell-MacQueen es una representación de DP y nos da una forma concreta de construirlo. Como veremos más adelante, este esquema es matemáticamente equivalente al Proceso de Restaurante Chino.

3.2 La construcción que rompe el palo

La construcción Stick -break es una forma alternativa de representar un proceso de Dirichlet que fue introducido por Sethuraman. Es una forma constructiva de formar el distribución y utiliza la siguiente analogía: Suponemos que tenemos un palo de longitud 1, lo rompemos en la posición β₁ y asignamos π₁ igual a la longitud de la parte del palo que rompimos. Repetimos el mismo proceso para obtener π₂, Pi₃,… Etc; debido a la forma en que se define este esquema podemos seguir haciéndolo infinitas veces.

Basado en lo anterior el π_k se puede modelar como , durante la cual la mientras que como en los esquemas anteriores los the son muestreados directamente por la distribución Base . En consecuencia, la distribución G se puede escribir como una suma de funciones delta ponderadas con π_k probabilidades que es igual a . Por lo tanto, la construcción Stick -break nos brinda una forma simple e intuitiva de construir un Proceso de Dirichlet.

3.3 El proceso del restaurante chino

El proceso de restaurante chino, que fue introducido por Aldous, es otra forma eficaz de representar un proceso de Dirichlet y se puede vincular directamente al esquema de urnas Blackwell-MacQueen. Este esquema utiliza el siguiente analogía: Suponemos que hay un restaurante chino con infinitas mesas. Cuando los clientes entran al restaurante, se sientan al azar en cualquiera de las mesas ocupadas o eligen sentarse en la primera mesa vacía disponible.

El CRP define una distribución en el espacio de particiones de los enteros positivos. Empezamos dibujando θ₁,… Θ_n del esquema de urnas de Blackwell-MacQueen. Como discutimos en los segmentos anteriores, esperamos ver un efecto de agrupamiento y, por lo tanto, el número total de valores únicos de θ k será significativamente menor que n. Por tanto, esto define una partición del conjunto {1,2,…, n} en k grupos. En consecuencia, dibujar a partir del esquema de urnas de Blackwell-MacQueen induce una partición aleatoria del conjunto {1,2,…, n}. El proceso del restaurante chino es inducido distribución sobre particiones. El algoritmo es como sigue:

· Empezamos con un restaurante vacío.

· 1^st el cliente se sienta siempre en 1^st mesa

· El n + 1^th el cliente tiene 2 opciones:

o Siéntese en la 1ra mesa desocupada con probabilidad

o Siéntese en cualquiera de las k-ésimas mesas ocupadas con probabilidad
donde es la cantidad de personas sentadas en esa mesa

Donde α es el valor de dispersión de DP yn es el número total de clientes en el restaurante en un momento dado. La variable latente z_i almacena el número de tabla de la i^th cliente y toma valores de 1 a k_n donde k_n es el número total de mesas ocupadas cuando hay n clientes en el restaurante. Debemos tener en cuenta que la k_n siempre será menor o igual an y en promedio se trata de . Finalmente, debemos tener en cuenta que la probabilidad de disposición de la mesa es invariante a las permutaciones. Así, la z_i es intercambiable, lo que implica que las mesas con el mismo tamaño de clientes tienen la misma probabilidad.

El Proceso de Restaurante Chino está fuertemente conectado al esquema de urnas de Pólya y al Proceso de Dirichlet. El CRP es una forma de especificar un distribución sobre particiones (asignaciones de tabla) de n puntos y se puede utilizar como a priori en el espacio de la variable latente z_i que determina las asignaciones del clúster. El CRP es equivalente al esquema de urnas de Pólya con la única diferencia de que no asigna parámetros a cada tabla / grupo. Ir de CRP al esquema de urnas de Pólya nosotros dibujamos para todas las tablas k = 1,2 ... y luego para cada x_i que se agrupa en la tabla z_i asignar un . En otras palabras, asigne a la nueva x_i el parámetro θ de la tabla. Finalmente desde no podemos asignar el θ a tablas infinitas desde el principio, podemos simplemente asignar un nuevo θ cada vez que alguien se sienta en una nueva mesa. Debido a todo lo anterior, el CRP puede ayudarnos a construir algoritmos computacionalmente eficientes para realizar análisis de conglomerados en conjuntos de datos.

En esta publicación, discutimos el Proceso de Dirichlet y varias formas de construirlo. Usaremos las ideas anteriores en el próximo artículo. Presentaremos el modelo de mezcla del proceso de Dirichlet y utilizaremos la representación de restaurante chino para construir el proceso de Dirichlet y preformar el análisis de conglomerados. Si se perdió algunos puntos, no se preocupe, las cosas comenzarán a aclararse con los dos artículos siguientes.

Espero que hayas encontrado interesante esta publicación. Si lo hizo, tómese un momento para compartirlo en Facebook y Twitter. 🙂