1ICFO-Institut de Ciencies Fotoniques, Instituto de Ciencia y Tecnología de Barcelona, 08860 Castelldefels, España
2CFIS-Centre de Formació Interdisciplinària Superior, UPC-Universitat Politècnica de Catalunya, 08028 Barcelona, España
3Universidad Grenoble Alpes, CNRS, Grenoble INP, Institut Néel, 38000 Grenoble, Francia
4ICREA-Institucio Catalana de Recerca i Estudis Avançats, Lluis Companys 23, 08010 Barcelona, España
¿Encuentra este documento interesante o quiere discutirlo? Scite o deje un comentario en SciRate.
Resumen
Las bases mutuamente imparciales corresponden a pares de medidas muy útiles en la teoría cuántica de la información. En la dimensión compuesta más pequeña, seis, se sabe que existen entre tres y siete bases mutuamente imparciales, con una conjetura de décadas de antigüedad, conocida como conjetura de Zauner, que establece que existen como máximo tres. Aquí abordamos la conjetura de Zauner numéricamente a través de la construcción de desigualdades de Bell para cada par de enteros $n,d ge 2$ que pueden violarse al máximo en la dimensión $d$ si y solo si existen $n$ MUB en esa dimensión. Por tanto, convertimos la conjetura de Zauner en un problema de optimización, que abordamos mediante tres métodos numéricos: optimización de balancín, programación semidefinida no lineal y técnicas de Monte Carlo. Los tres métodos identifican correctamente los casos conocidos en dimensiones bajas y todos sugieren que no existen cuatro bases mutuamente imparciales en la dimensión seis, y todas encuentran las mismas bases que optimizan numéricamente la desigualdad de Bell correspondiente. Además, estos optimizadores numéricos parecen coincidir con las "cuatro bases más distantes" en la dimensión seis, que se encuentran mediante la optimización numérica de una medida de distancia en [P. Raynal, X. Lü, B.-G. Englert, {Phys. Rev. A}, { 83} 062303 (2011)]. Finalmente, los resultados de Monte Carlo sugieren que existen como máximo tres MUB en la dimensión diez.
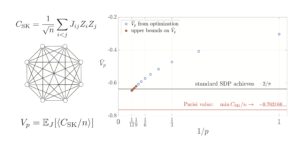
Imagen destacada: La diferencia relativa entre el valor de nuestras desigualdades de Bell suponiendo que existen n MUB en la dimensión d y el valor encontrado por nuestros métodos numéricos. Los valores cero significan que los métodos encontraron n MUB en la dimensión d, mientras que los valores distintos de cero significan que los métodos no encontraron n MUB en la dimensión d. Todos los casos conocidos (dimensiones dos a cinco y dimensión seis con dos y tres MUB) están correctamente identificados por los números. En la dimensión seis, ninguno de los métodos encuentra cuatro MUB y todos los métodos convergen en el mismo conjunto de cuatro bases.
Resumen popular
A pesar de su amplio uso, aún quedan preguntas abiertas con respecto a la estructura de los MUB. Lo más destacado es que se desconoce el número máximo de mediciones que son imparciales por pares ("el número de MUB") si la dimensión del sistema cuántico es un número compuesto. En particular, en la dimensión seis solo sabemos que el número de MUB está entre tres y siete. Una conjetura abierta desde hace mucho tiempo es la de Zauner, que afirma que no existen más de tres MUB en la dimensión seis. Esta conjetura de décadas está respaldada por alguna evidencia numérica, pero no existe prueba hasta el día de hoy.
En este trabajo abordamos la conjetura de Zauner a través de la no localidad de Bell. La no localidad de Bell se refiere a dos experimentadores que no pueden comunicarse, pero pueden compartir algunas correlaciones en forma de aleatoriedad clásica o un estado cuántico compartido. Se ha demostrado que compartir recursos cuánticos puede conducir a datos experimentales que no pueden ser explicados por la física clásica (más precisamente, por los llamados modelos de variables ocultas locales). Esto se conoce como teorema de Bell y ha sido verificado experimentalmente en la última década. Presenciar la no clásicaidad de los datos experimentales se realiza más comúnmente a través de las llamadas desigualdades de Bell, que son funciones de las probabilidades de resultado de la medición que ocurren en el experimento. Los datos clásicos deben satisfacer las desigualdades de Bell, mientras que los datos cuánticos pueden violarlas.
Recientemente, se han encontrado desigualdades de Bell que se violan al máximo si una de las partes emplea un par de medidas MUB de una dimensión dada. En este trabajo, extendemos estas desigualdades a otras nuevas, violadas al máximo por un número seleccionado de medidas MUB en una dimensión dada. Además, si la dimensión en el experimento es fija, la violación máxima se obtiene si y solo si las medidas empleadas corresponden al número seleccionado de MUB en la dimensión dada. Por lo tanto, decidir si existe un número seleccionado de MUB en una dimensión dada es equivalente a encontrar la violación máxima de la desigualdad de Bell correspondiente en esta dimensión fija.
Si bien encontrar esta violación máxima es en general un problema difícil, empleamos tres métodos numéricos diferentes como un intento de encontrar la violación máxima de nuestras desigualdades de Bell en una dimensión fija. Dos de estos métodos son variantes de las técnicas de programación semidefinida, mientras que el tercero está inspirado en la física estadística y se denomina recocido simulado. Si bien todos estos métodos son heurísticos, es decir, no hay garantía de que encuentren el verdadero óptimo del problema, uno puede medir su rendimiento aplicándolos a problemas de optimización cuyo óptimo se conoce. En particular, encontramos que los tres métodos pueden identificar correctamente las mediciones de MUB en los casos en que se sabe que existen. Además, en los casos en los que se sabe que no existen, los tres métodos convergen en el mismo conjunto de medidas hasta la precisión numérica. Luego aplicamos nuestros métodos al primer caso desconocido, es decir, cuatro MUB en la dimensión seis. Ninguno de los métodos puede identificar cuatro MUB en la dimensión seis, pero nuevamente todos convergen en el mismo conjunto de cuatro mediciones con precisión numérica. Además, la técnica de recocido simulado no encuentra cuatro MUB en la siguiente dimensión compuesta, la dimensión diez. Por lo tanto, aunque no se pueden hacer afirmaciones rigurosas debido a la naturaleza heurística de nuestras técnicas, nuestros resultados respaldan la conjetura de Zauner desde la nueva perspectiva de la no localidad de Bell.
► datos BibTeX
► referencias
[ 1 ] DNI Ivanovic. Descripción geométrica de la determinación del estado cuántico. Journal of Physics A: Mathematical and General, 14(12):3241–3245, 1981. doi:10.1088/0305-4470/14/12/019.
https://doi.org/10.1088/0305-4470/14/12/019
[ 2 ] G. Brassard CH Bennett. Criptografía cuántica: distribución de claves públicas y lanzamiento de monedas. Actas de la Conferencia internacional IEEE sobre computadoras, sistemas y procesamiento de señales (IEEE, 1984), 175:8, 1984. doi:10.1016/j.tcs.2011.08.039.
https: / / doi.org/ 10.1016 / j.tcs.2011.08.039
[ 3 ] Artur K. Ekert. Criptografía cuántica basada en el teorema de Bell. física Rev. Lett., 67:661–663, 1991. doi:10.1103/PhysRevLett.67.661.
https: / / doi.org/ 10.1103 / PhysRevLett.67.661
[ 4 ] Dagmar Bruss. Espionaje óptimo en criptografía cuántica con seis estados. física Rev. Lett., 81:3018–3021, 1998. doi:10.1103/PhysRevLett.81.3018.
https: / / doi.org/ 10.1103 / PhysRevLett.81.3018
[ 5 ] Armin Tavakoli, Alley Hameedi, Breno Marques y Mohamed Bourennane. Códigos cuánticos de acceso aleatorio utilizando sistemas de un solo nivel $d$. física Rev. Lett., 114:170502, 2015. doi:10.1103/PhysRevLett.114.170502.
https: / / doi.org/ 10.1103 / PhysRevLett.114.170502
[ 6 ] Máté Farkas y Jędrzej Kaniewski. Bases de autoevaluación mutuamente imparciales en el escenario de preparación y medición. física Rev. A, 99:032316, 2019. doi:10.1103/PhysRevA.99.032316.
https: / / doi.org/ 10.1103 / PhysRevA.99.032316
[ 7 ] H. Bechmann-Pasquinucci y N. Gisin. Desigualdad de Bell para quunits con medidas binarias. Información cuántica. Comput., 3(2):157–164, 2003. doi:10.26421/QIC3.2-6.
https: / / doi.org/ 10.26421 / QIC3.2-6
[ 8 ] Jędrzej Kaniewski, Ivan Šupić, Jordi Tura, Flavio Baccari, Alexia Salavrakos y Remigiusz Augusiak. No localidad máxima a partir de entrelazamiento máximo y bases mutuamente imparciales, y autoevaluación de sistemas cuánticos de dos qutrit. Cuántica, 3:198, 2019. doi:10.22331/q-2019-10-24-198.
https://doi.org/10.22331/q-2019-10-24-198
[ 9 ] Armin Tavakoli, Máté Farkas, Denis Rosset, Jean-Daniel Bancal y Jędrzej Kaniewski. Bases mutuamente imparciales y medidas simétricas completas informativamente en los experimentos de Bell. Avances científicos, 7(7):eabc3847, 2021. doi:10.1126/sciadv.abc3847.
https:///doi.org/10.1126/sciadv.abc3847
[ 10 ] Thomas Durt, Berthold-Georg Englert, Ingemar Bengtsson y Karol Życzkowski. Sobre bases mutuamente imparciales. Revista internacional de información cuántica, 08(04):535–640, 2010. doi:10.1142/S0219749910006502.
https: / / doi.org/ 10.1142 / S0219749910006502
[ 11 ] William K Wootters y Brian D Fields. Determinación del estado óptimo mediante mediciones mutuamente imparciales. Annals of Physics, 191(2):363–381, 1989. doi:10.1016/0003-4916(89)90322-9.
https://doi.org/10.1016/0003-4916(89)90322-9
[ 12 ] Paweł Wocjan y Thomas Beth. Nueva construcción de bases mutuamente imparciales en dimensiones cuadradas. Información cuántica. Comput., 5(2):93–101, 2005. doi:10.26421/QIC5.2-1.
https: / / doi.org/ 10.26421 / QIC5.2-1
[ 13 ] Mihály Weiner. Una brecha para el número máximo de bases mutuamente imparciales. proc. Amer. Matemáticas. Soc., 141:1963–1969, 2013. doi:10.1090/S0002-9939-2013-11487-5.
https://doi.org/10.1090/S0002-9939-2013-11487-5
[ 14 ] Gerhard Zauner. Quantendesigns: Grundzüge einer nichtkommutativen Designtheorie. Tesis doctoral, 1999.
[ 15 ] P. Oscar Boykin, Meera Sitharam, Pham Huu Tiep y Pawel Wocjan. Bases mutuamente imparciales y descomposiciones ortogonales de álgebras de Lie. Información cuántica. Comput., 7(4):371–382, 2007. doi:10.26421/QIC7.4-6.
https: / / doi.org/ 10.26421 / QIC7.4-6
[ 16 ] Stephen Brierley y Stefan Weigert. Construyendo bases mutuamente imparciales en la dimensión seis. física Rev.A, 79:052316, 2009. doi:10.1103/PhysRevA.79.052316.
https: / / doi.org/ 10.1103 / PhysRevA.79.052316
[ 17 ] Philippe Jaming, Máté Matolcsi, Péter Móra, Ferenc Szöllősi y Mihály Weiner. Un problema de Pauli generalizado y una familia infinita de MUB-tripletes en dimensión 6. Journal of Physics A: Mathematical and Theoretical, 42(24):245305, mayo de 2009. doi:10.1088/1751-8113/42/24/ 245305.
https://doi.org/10.1088/1751-8113/42/24/245305
[ 18 ] Gary McConnell, Harry Spencer y Afaq Tahir. Evidencia a favor y en contra de la conjetura MUB de Zauner en $mathbb{C}^6$. 2021. doi:10.48550/arXiv.2103.08703.
https:///doi.org/10.48550/arXiv.2103.08703
[ 19 ] Sander Gribling y Sven Polak. Bases mutuamente insesgadas: optimización polinomial y simetría. 2021. doi:10.48550/arXiv.2111.05698.
https:///doi.org/10.48550/arXiv.2111.05698
[ 20 ] Ingemar Bengtsson, Wojciech Bruzda, Åsa Ericsson, Jan-Åke Larsson, Wojciech Tadej y Karol Życzkowski. Bases mutuamente insesgadas y matrices de Hadamard de orden seis. Revista de Física Matemática, 48(5):052106, 2007. doi:10.1063/1.2716990.
https: / / doi.org/ 10.1063 / 1.2716990
[ 21 ] Philippe Raynal, Xin Lü y Berthold-Georg Englert. Bases mutuamente imparciales en seis dimensiones: Las cuatro bases más distantes. física Rev.A, 83:062303, 2011. doi:10.1103/PhysRevA.83.062303.
https: / / doi.org/ 10.1103 / PhysRevA.83.062303
[ 22 ] Edgar A. Aguilar, Jakub J. Borkała, Piotr Mironowicz y Marcin Pawłowski. Conexiones entre bases mutuamente imparciales y códigos cuánticos de acceso aleatorio. física Rev. Lett., 121:050501, 2018. doi:10.1103/PhysRevLett.121.050501.
https: / / doi.org/ 10.1103 / PhysRevLett.121.050501
[ 23 ] Nicolas Brunner, Daniel Cavalcanti, Stefano Pironio, Valerio Scarani y Stephanie Wehner. Bell no localidad. Rev. Mod. Phys., 86: 419–478, 2014. doi: 10.1103 / RevModPhys.86.419.
https: / / doi.org/ 10.1103 / RevModPhys.86.419
[ 24 ] MOSEK ApS. API de MOSEK Fusion para C++ 9.2.49, 2021. URL: https://docs.mosek.com/9.2/cxxfusion/index.html.
https:///docs.mosek.com/9.2/cxxfusion/index.html
[ 25 ] Hiroshi Yamashita, Hiroshi Yabe y Kouhei Harada. Un método de punto interior primal-dual para programación semidefinida no lineal. Programación matemática, 135(1):89–121, 2012. doi:10.1007/s10107-011-0449-z.
https: / / doi.org/ 10.1007 / s10107-011-0449-z
[ 26 ] Stephen Boyd y Lieven Vandenberghe. Optimizacion convexa. Cambridge University Press, 2004. doi: 10.1017 / CBO9780511804441.
https: / / doi.org/ 10.1017 / CBO9780511804441
[ 27 ] S. Kirkpatrick, CD Gelatt y MP Vecchi. Optimización por recocido simulado. Science, 220(4598):671–680, 1983. doi:10.1126/science.220.4598.671.
https: / / doi.org/ 10.1126 / science.220.4598.671
[ 28 ] Nicholas Metropolis, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller y Edward Teller. Ecuación de cálculos de estado por máquinas de computación rápida. The Journal of Chemical Physics, 21(6):1087–1092, 1953. doi:10.1063/1.1699114.
https: / / doi.org/ 10.1063 / 1.1699114
[ 29 ] Miguel Navascués, Stefano Pironio, and Antonio Acín. Acotar el conjunto de correlaciones cuánticas. física Rev. Lett., 98:010401, 2007. doi:10.1103/PhysRevLett.98.010401.
https: / / doi.org/ 10.1103 / PhysRevLett.98.010401
Citado por
Este documento se publica en Quantum bajo el Creative Commons Reconocimiento 4.0 Internacional (CC BY 4.0) licencia. Los derechos de autor permanecen con los titulares de derechos de autor originales, como los autores o sus instituciones.