Big O notation ja algoritmi analüüs Pythoni näidetega

Sissejuhatus

Tavaliselt on probleemi lahendamiseks arvutiprogrammi abil mitu võimalust. Näiteks massiivi üksuste sortimiseks on mitu võimalust – saate kasutada liita sort, mulli sorteerimine, sisestamise sort, ja nii edasi. Kõigil neil algoritmidel on oma plussid ja miinused ning arendaja ülesanne on neid kaaluda, et oleks võimalik valida igal kasutusjuhul kasutatav parim algoritm. Teisisõnu, põhiküsimus on selles, millist algoritmi kasutada konkreetse probleemi lahendamiseks, kui probleemile on mitu lahendust.

Algoritmi analüüs viitab erinevate algoritmide keerukuse analüüsile ja kõige tõhusama algoritmi leidmisele käsil oleva probleemi lahendamiseks. Big-O märge on statistiline mõõt, mida kasutatakse algoritmi keerukuse kirjeldamiseks.

Selles juhendis teeme kõigepealt lühikese ülevaate algoritmi analüüsist ja seejärel vaatame põhjalikumalt Big-O tähistust. Vaatame, kuidas Big-O tähistust saab kasutada erinevate Pythoni funktsioonide abil algoritmi keerukuse leidmiseks.

Miks on algoritmi analüüs oluline?

Et mõista, miks algoritmanalüüs on oluline, võtame appi lihtsa näite. Oletame, et juht annab kahele oma töötajale ülesande koostada Pythonis algoritm, mis arvutab kasutaja sisestatud arvu faktoriaali. Esimese töötaja välja töötatud algoritm näeb välja selline:

def fact(n):
    product = 1
    for i in range(n):
        product = product * (i+1)
    return product

print(fact(5))

Pange tähele, et algoritm võtab argumendina lihtsalt täisarvu. Sees fact() funktsioon muutuja nimega product on initsialiseeritud 1. Tsükkel käivitatakse alates 1 et n ja iga iteratsiooni ajal väärtust product korrutatakse tsükliga itereeritava arvuga ja tulemus salvestatakse product jälle muutuv. Pärast tsükli käivitamist product muutuja sisaldab faktoriaali.

Samamoodi töötas ka teine ​​töötaja välja algoritmi, mis arvutab arvu faktoriaali. Teine töötaja kasutas arvu faktoriaali arvutamiseks rekursiivset funktsiooni n:

def fact2(n):
    if n == 0:
        return 1
    else:
        return n * fact2(n-1)

print(fact2(5))

Juht peab otsustama, millist algoritmi kasutada. Selleks on nad otsustanud valida, milline algoritm töötab kiiremini. Üks võimalus seda teha on leida samal sisendil koodi täitmiseks kuluv aeg.

Jupyteri märkmikus saate kasutada %timeit sõnasõna, millele järgneb funktsioonikutse, et leida funktsiooni täitmiseks kulunud aeg:

%timeit fact(50)

See annab meile:

9 µs ± 405 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Väljund ütleb, et algoritm võtab 9 mikrosekundit (pluss/miinus 45 nanosekundit) tsükli kohta.

Samamoodi saame arvutada, kui palju aega kulub teise lähenemisviisi täitmiseks:

%timeit fact2(50)

Selle tulemuseks on:

15.7 µs ± 427 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Teine algoritm, mis hõlmab rekursiooni, võtab 15 mikrosekundit (pluss/miinus 427 nanosekundit).

Täitmisaeg näitab, et esimene algoritm on kiirem võrreldes teise rekursiooni sisaldava algoritmiga. Suurte sisenditega tegelemisel võib jõudluse erinevus muutuda olulisemaks.

Täitmisaeg ei ole aga hea mõõdik algoritmi keerukuse mõõtmiseks, kuna see sõltub riistvarast. Algoritmi jaoks on vaja objektiivsemat keerukuse analüüsi mõõdikut. See on koht, kus Suur O-tähis tuleb mängida.

Algoritmi analüüs Big-O märkega

Big-O tähistus tähistab seost algoritmi sisendi ja algoritmi täitmiseks vajalike sammude vahel. Seda tähistatakse suure O-tähega, millele järgneb ava- ja sulgesulg. Sulgudes esitatakse sisendi ja algoritmi sammude vaheline seos, kasutades "n".

Peamine on see, et Big-O ei ole huvitatud a eriline näide, kus käivitate algoritmi, näiteks fact(50), vaid pigem seda, kui hästi see õnnestub skaala antud kasvavat sisendit. See on palju parem mõõdik hindamiseks kui konkreetse juhtumi konkreetne aeg!

Näiteks kui on olemas a lineaarne suhe sisendi ja algoritmi poolt selle täitmise lõpuleviimiseks tehtud sammu vahel kasutatakse Big-O tähistust O (n). Samamoodi on Big-O tähistus jaoks ruutfunktsioonid is O(n²).

Intuitsiooni loomiseks:

• O (n): kell n=1, 1 samm on tehtud. Kell n=10, tehakse 10 sammu.
• O(n²): kell n=1, 1 samm on tehtud. Kell n=10, tehakse 100 sammu.

At n=1, toimiksid need kaks sama! See on veel üks põhjus, miks sisendi ja selle sisendi töötlemise sammude arvu vahelise seose jälgimine on parem kui lihtsalt funktsioonide hindamine mõne konkreetse sisendiga.

Järgmised on mõned kõige levinumad Big-O funktsioonid.

Nimi	Suur O
Pidev	O (c)
Linear	O (n)
Nelinurkne	O(n²)
Kuubikujuline	O(n³)
Eksponent-	O(2)
Logaritmiline	O (log (n))
Logi lineaarne	O(nlog(n))

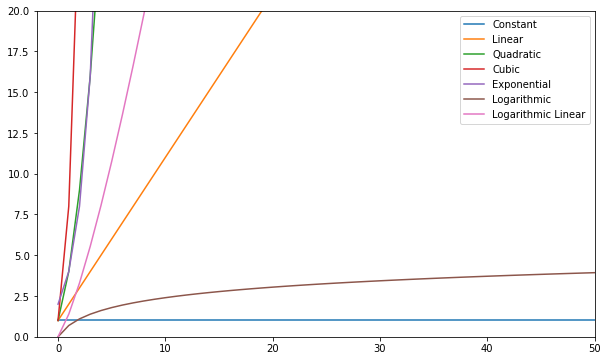
Saate neid funktsioone visualiseerida ja võrrelda:

Üldiselt võib öelda, et kõike, mis on lineaarne, loetakse halvaks keerukuseks (st ebaefektiivseks) ja seda tuleks võimalusel vältida. Lineaarne keerukus on okei ja tavaliselt vajalik pahe. Logaritmiline on hea. Constant on hämmastav!

Et saada aimu, kuidas Big-O arvutatakse, vaatame mõnda konstantse, lineaarse ja ruutkeskmise keerukuse näidet.

Pidev keerukus - O(C)

Algoritmi keerukust peetakse konstantseks, kui algoritmi täitmiseks vajalikud sammud jäävad konstantseks, sõltumata sisendite arvust. Pidevat keerukust tähistab O (c) kus c võib olla mis tahes konstantne arv.

Kirjutame Pythonis lihtsa algoritmi, mis leiab loendist esimese elemendi ruudu ja prindib selle siis ekraanile:

def constant_algo(items):
    result = items[0] * items[0]
    print(result)

constant_algo([4, 5, 6, 8])

Ülaltoodud skriptis sõltumata sisendi suurusestvõi sisestusloendis olevate üksuste arv items, täidab algoritm ainult 2 sammu:

1. Esimese elemendi ruudu leidmine
2. Tulemuse printimine ekraanile.

Seetõttu jääb keerukus konstantseks.

Kui joonistate joondiagrammi erineva suurusega items sisestades X-teljel ja sammude arvu Y-teljel, saad sirge. Loome lühikese skripti, mis aitab meil seda visualiseerida. Olenemata sisendite arvust jääb teostatud sammude arv samaks:

steps = []
def constant(n):
    return 1
    
for i in range(1, 100):
    steps.append(constant(i))
plt.plot(steps)

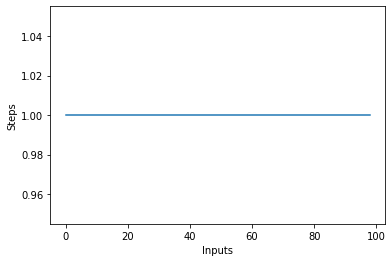
Lineaarne keerukus - O (n)

Algoritmi keerukust peetakse lineaarseks, kui algoritmi täitmiseks vajalikud sammud suurenevad või vähenevad lineaarselt sisendite arvuga. Lineaarne keerukus on tähistatud O (n).

Selles näites kirjutame lihtsa programmi, mis kuvab kõik loendis olevad üksused konsooli:

def linear_algo(items):
    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Selle keerukus linear_algo() funktsioon on ülaltoodud näites lineaarne, kuna for-tsükli iteratsioonide arv on võrdne sisendi suurusega items massiivi. Näiteks kui selles on 4 üksust items loendis käivitatakse for-loop 4 korda.

Koostame kiiresti lineaarse keerukuse algoritmi graafiku sisendite arvuga x-teljel ja sammude arvuga y-teljel:

steps = []
def linear(n):
    return n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

Selle tulemuseks on:

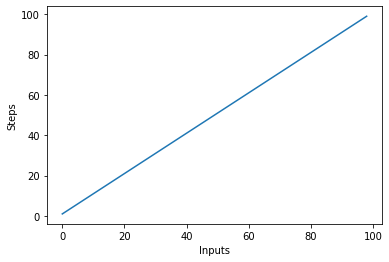
Oluline on märkida, et suurte sisendite korral kipuvad konstandid väärtust kaotama. Seetõttu eemaldame tavaliselt konstandid Big-O tähistusest ja avaldist nagu O(2n) lühendatakse tavaliselt O(n)-ks. Nii O(2n) kui ka O(n) on lineaarsed – oluline on lineaarne seos, mitte konkreetne väärtus. Näiteks muutkem linear_algo():

def linear_algo(items):
    for item in items:
        print(item)

    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Seal on kaks for-tsüklit, mis korduvad üle sisendi items nimekirja. Seetõttu muutub algoritmi keerukus O (2n), aga sisendloendis olevate lõpmatute üksuste puhul võrdub lõpmatuse kaks korda ikkagi lõpmatusega. Me võime konstanti ignoreerida 2 (kuna see on lõppkokkuvõttes tähtsusetu) ja algoritmi keerukus jääb alles O (n).

Visualiseerime seda uut algoritmi, joonistades sisendid X-teljele ja sammude arvu Y-teljel:

steps = []
def linear(n):
    return 2*n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

Ülaltoodud skriptist näete seda selgelt y=2nväljund on aga lineaarne ja näeb välja selline:

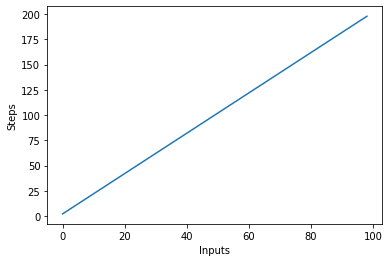
Ruutiline keerukus - O(n²)

Algoritmi keerukust peetakse ruutkeskseks, kui algoritmi täitmiseks vajalikud sammud on sisendis olevate üksuste arvu ruutfunktsioon. Ruut keerukus on tähistatud kui O(n²):

def quadratic_algo(items):
    for item in items:
        for item2 in items:
            print(item, ' ' ,item2)

quadratic_algo([4, 5, 6, 8])

Meil on välimine silmus, mis kordab kõiki sisestusloendis olevaid üksusi, ja seejärel pesastatud sisesilmus, mis taas kordab kõiki sisestusloendi üksusi. Tehtud sammude koguarv on n*n, kus n on üksuste arv sisendmassiivis.

Järgmine graafik kujutab ruutkeskmise keerukusega algoritmi sisendite arvu ja etappe:

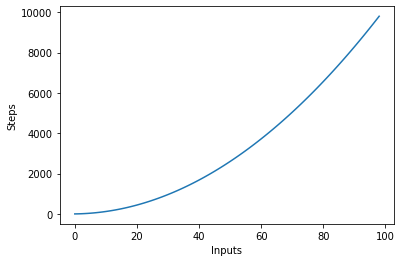
Logaritmiline keerukus - O (logn)

Mõned algoritmid saavutavad logaritmilise keerukuse, näiteks Binaarotsing. Binaarne otsing otsib massiivist elementi, märgistades kesk- massiivi ja selle poole kärpimine, milles elementi ei ole. See teeb seda ülejäänud poole jaoks uuesti ja jätkab samu samme, kuni element on leitud. Igal sammul see pooled elementide arv massiivis.

Selleks on vaja massiivi sortida ja teha andmete kohta oletus (näiteks, et need on sorteeritud).

Kui saate sissetulevate andmete kohta oletusi teha, saate astuda samme, mis vähendavad algoritmi keerukust. Soovitav on logaritmiline keerukus, kuna see saavutab hea jõudluse isegi suure skaleeritud sisendiga.

Keeruliste funktsioonide keerukuse leidmine?

Eelmistes näidetes olid meil sisendil üsna lihtsad funktsioonid. Kuidas aga arvutada funktsioonide Big-O, mis kutsuvad (mitu) sisendis muid funktsioone?

Vaatame:

def complex_algo(items):

    for i in range(5):
        print("Python is awesome")

    for item in items:
        print(item)

    for item in items:
        print(item)

    print("Big O")
    print("Big O")
    print("Big O")

complex_algo([4, 5, 6, 8])

Ülaltoodud skriptis tehakse mitmeid ülesandeid, esiteks prinditakse konsoolile string 5 korda, kasutades print avaldus. Järgmisena trükime sisestusloendi kaks korda ekraanile ja lõpuks trükitakse konsoolile kolm korda veel üks string. Sellise algoritmi keerukuse leidmiseks peame algoritmi koodi osadeks jaotama ja proovima leida üksikute tükkide keerukust. Märkige iga tüki keerukus.

Esimeses jaotises on meil:

for i in range(5):
	print("Python is awesome")

Selle osa keerukus on O (5) kuna selles kooditükis tehakse viis konstantset sammu olenemata sisendist.

Järgmisena on meil:

for item in items:
	print(item)

Teame, et ülaltoodud koodiosa keerukus on O (n). Samamoodi on ka järgmise koodilõigu keerukus O (n):

for item in items:
	print(item)

Lõpuks trükitakse järgmises kooditükis string kolm korda, seega on keerukus O (3):

print("Big O")
print("Big O")
print("Big O")

Üldise keerukuse leidmiseks peame lihtsalt lisama need individuaalsed keerukused:

O(5) + O(n) + O(n) + O(3)

Ülaltoodut lihtsustades saame:

O(8) + O(2n) = O(8+2n)

Varem ütlesime, et kui sisend (millel on antud juhul pikkus n) muutub ülisuureks, muutuvad konstandid tähtsusetuks, st kaks korda või pool lõpmatusest jääb ikkagi lõpmatuseks. Seetõttu võime konstante ignoreerida. Algoritmi lõplik keerukus on O (n)!

Halvima vs parima juhtumi keerukus

Tavaliselt, kui keegi küsib teilt algoritmi keerukuse kohta, on ta huvitatud halvima juhtumi keerukusest (Big-O). Mõnikord võivad nad olla huvitatud ka parimal juhul keerukusest (Big-Omega).

Nende vahelise seose mõistmiseks vaatame veel üht koodilõiku:

def search_algo(num, items):
    for item in items:
        if item == num:
            return True
        else:
            pass
nums = [2, 4, 6, 8, 10]

print(search_algo(2, nums))

Ülaltoodud skriptis on meil funktsioon, mis võtab sisendiks numbri ja numbrite loendi. Tagastab tõene, kui edastatud number leitakse numbrite loendist, vastasel juhul tagastab see None. Kui otsite loendist 2, leitakse see esimeses võrdluses. See on algoritmi parimal juhul keerukus, kuna otsitav üksus leitakse esimesest otsitud registrist. Parima juhtumi keerukus, antud juhul on O (1). Teisest küljest, kui otsite 10, leitakse see viimati otsitud registrist. Algoritm peab seega otsima läbi kõik loendis olevad üksused halvimal juhul keerukus muutub O (n).

Lisaks parima ja halvima juhtumi keerukusele saate ka arvutada keskmine keerukus (Big-Theta) algoritmi, mis ütleb teile "juhusliku sisendi korral milline on algoritmi eeldatav ajaline keerukus"?

Ruumi keerukus

Lisaks ajalisele keerukusele, kus loendate algoritmi täitmiseks vajalike sammude arvu, leiate ka ruumi keerukus mis viitab ruumi mahule, mida peate programmi täitmise ajal mälus eraldama.

Vaadake järgmist näidet:

def return_squares(n):
    square_list = []
    for num in n:
        square_list.append(num * num)

    return square_list

nums = [2, 4, 6, 8, 10]
print(return_squares(nums))

. return_squares() funktsioon aktsepteerib täisarvude loendit ja tagastab loendi vastavate ruutudega. Algoritm peab eraldama mälu sama arvu üksuste jaoks kui sisendloendis. Seetõttu muutub algoritmi ruumiline keerukus O (n).

Järeldus

Big-O tähistus on standardne mõõdik, mida kasutatakse algoritmi keerukuse mõõtmiseks. Selles juhendis uurisime, mis on Big-O tähistus ja kuidas seda saab kasutada mitmesuguste algoritmide keerukuse mõõtmiseks. Samuti uurisime erinevate Pythoni näidete abil erinevat tüüpi Big-O funktsioone. Lõpuks vaatasime lühidalt halvima ja parima juhtumi keerukust koos ruumi keerukusega.