Uus läbimurre toob maatrikskorrutamise ideaalile lähemale | Quanta ajakiri

Arvutiteadlased on nõudlik kamp. Nende jaoks ei piisa probleemile õige vastuse saamisest – peaaegu alati on eesmärk saada vastus võimalikult tõhusalt.

Võtke maatriksite või arvumassiivide korrutamine. 1812. aastal tuli prantsuse matemaatik Jacques Philippe Marie Binet välja põhireeglitega, mida me õpilastele siiani õpetame. See töötab suurepäraselt, kuid teised matemaatikud on leidnud viise protsessi lihtsustamiseks ja kiirendamiseks. Nüüd ülesanne protsessi kiirendamine maatriksi korrutamise punkt asub matemaatika ja arvutiteaduse ristumiskohas, kus teadlased jätkavad protsessi täiustamist tänapäevani – kuigi viimastel aastakümnetel on kasu olnud üsna tagasihoidlik. Alates 1987. aastast on maatriksikorrutamise arvulised täiustused olnud "väikesed ja … äärmiselt raskesti saavutatavad", ütles ta. François Le Gall, Nagoya ülikooli arvutiteadlane.

Nüüd on kolm teadlast – Ran Duan ja Renfei Zhou Tsinghua ülikoolist ning Hongxun Wu California ülikoolist Berkeleyst – astunud suure sammu edasi selle igavese probleemi lahendamisel. Nende uued tulemused, mida esitleti eelmise aasta novembris arvutiteaduse aluste konverentsil, tulenevad ootamatust uuest tehnikast, ütles Le Gall. Kuigi parendus ise oli suhteliselt väike, nimetas Le Gall seda "kontseptsiooniliselt suuremaks kui teised eelmised".

Tehnika paljastab varem tundmatu ja seega kasutamata potentsiaalsete paranduste allika ning see on juba vilja kandnud: Teine paberJaanuaris avaldatud raamat tugineb esimesele, mis näitab, kuidas maatrikskorrutamist saab veelgi suurendada.

"See on suur tehniline läbimurre," ütles William Kuszmaul, Harvardi ülikooli teoreetiline arvutiteadlane. "See on maatriksi korrutamise suurim paranemine, mida oleme näinud rohkem kui kümne aasta jooksul."

Sisenege Maatriksisse

See võib tunduda ebaselge probleemina, kuid maatrikskorrutamine on põhiline arvutusoperatsioon. See on sisse lülitatud suur osa algoritmidest, mida inimesed kasutavad iga päev mitmesuguste ülesannete jaoks, alates teravama arvutigraafika kuvamisest kuni võrguteooria logistiliste probleemide lahendamiseni. Ja nagu ka teistes arvutusvaldkondades, on kiirus esmatähtis. Isegi väikesed täiustused võivad lõpuks kaasa tuua märkimisväärse aja, arvutusvõimsuse ja raha kokkuhoiu. Kuid praegu huvitab teoreetikuid peamiselt see, kui kiiresti see protsess võib olla.

Traditsiooniline kahe korrutamise viis n-kõrval-n maatriksid – korrutades esimese maatriksi iga rea ​​numbrid teise maatriksi veergude arvudega – nõuavad n³ eraldi korrutised. 2 korda 2 maatriksite puhul tähendab see 2³ või 8 korrutamist.

1969. aastal paljastas matemaatik Volker Strassen keerukama protseduuri, mis võimaldab korrutada 2 korda 2 maatriksit vaid seitsme korrutusastmega ja 18 liitmisega. Kaks aastat hiljem näitas arvutiteadlane Shmuel Winograd, et seitse on tõepoolest 2x2 maatriksite absoluutne miinimum.

Strassen kasutas seda sama ideed, et näidata, et kõik on suurem n-kõrval-n maatrikseid saab korrutada ka vähemaga kui n³ sammud. Selle strateegia põhielement hõlmab protseduuri, mida nimetatakse dekompositsiooniks – suure maatriksi jagamine järjest väiksemateks alammaatriksiteks, mis võivad olla nii väikesed kui 2x2 või isegi 1x1 (need on vaid üksikud arvud).

Hiiglasliku massiivi pisikesteks tükkideks jagamise põhjendus on nende sõnul üsna lihtne Virginia Vassilevska Williams, Massachusettsi Tehnoloogiainstituudi arvutiteadlane ja ühe uue artikli kaasautor. "Inimesel on raske vaadata suurt maatriksit (näiteks suurusjärgus 100 korda 100) ja mõelda parimale võimalikule algoritmile," ütles Vassilevska Williams. Isegi kolm korda kolm maatriksit pole veel täielikult lahendatud. "Siiski saab kasutada kiiret algoritmi, mis on juba välja töötatud väikeste maatriksite jaoks, et saada kiire algoritm ka suuremate maatriksite jaoks."

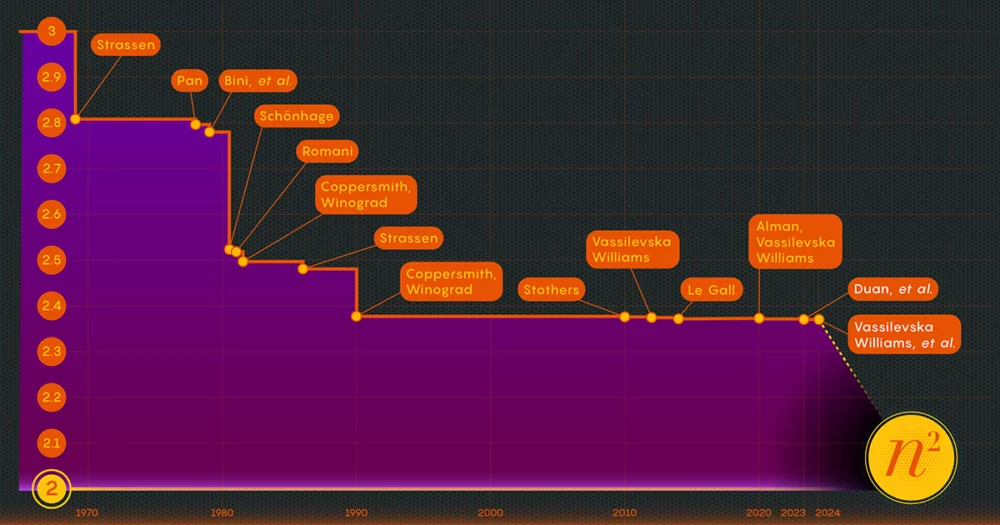
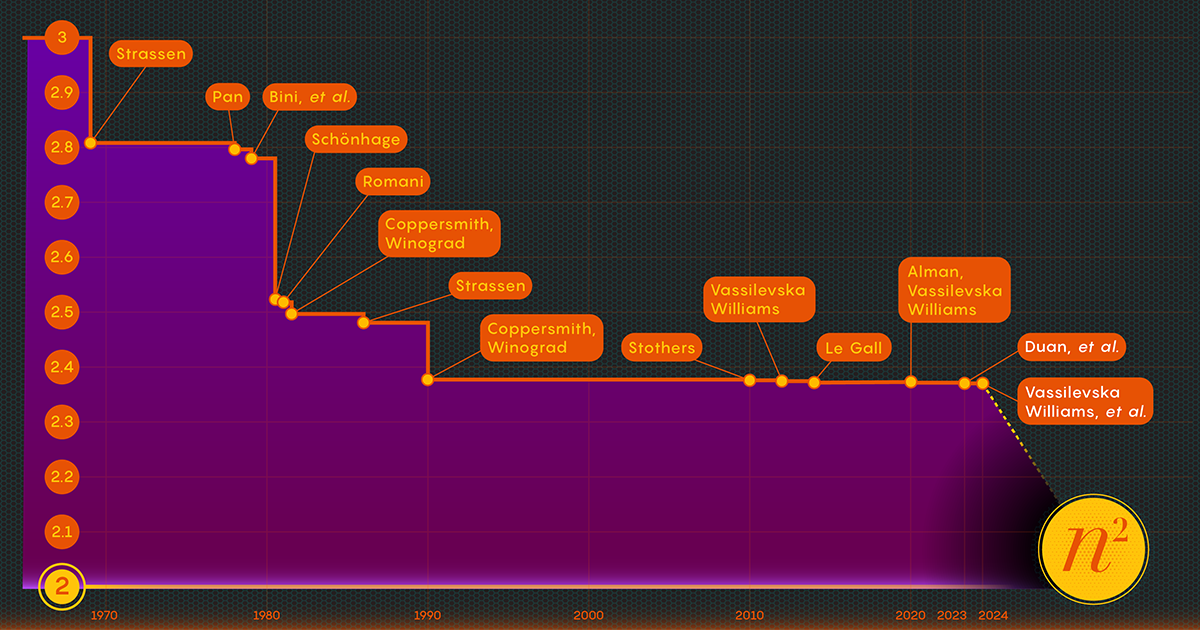
Teadlased on kindlaks teinud, et kiiruse võti on korrutamisetappide arvu vähendamine, vähendades seda eksponenti n³ (standardmeetodi puhul) nii palju kui võimalik. Madalaim võimalik väärtus, n², on põhimõtteliselt nii pikk, kui kulub vastuse kirjutamiseks. Arvutiteadlased viitavad sellele eksponendile kui oomega, ω, koos n^ω olles võimalikult vähe samme, mida on vaja kahe edukaks korrutamiseks n-kõrval-n maatriksid nagu n kasvab väga suureks. "Selle töö mõte," ütles Zhou, kes oli ka 2024. aasta jaanuari dokumendi kaasautor, "vaadata, kui lähedale kahele võite jõuda ja kas seda on võimalik teoorias saavutada."

Laserfookus

1986. aastal tegi Strassen veel ühe suure läbimurde, kui ta sisse mida nimetatakse maatriksi korrutamise lasermeetodiks. Strassen kasutas seda oomega ülemise väärtuse 2.48 määramiseks. Kuigi see meetod on vaid üks samm suurtes maatriksikorrutistes, on see üks olulisemaid, kuna teadlased on seda jätkuvalt täiustanud.

Aasta hiljem tutvustasid Winograd ja Don Coppersmith uut algoritmi, mis täiendas kaunilt lasermeetodit. Seda tööriistade kombinatsiooni on kasutatud peaaegu kõigis järgnevates maatriksikorrutamise kiirendamise jõupingutustes.

Siin on lihtsustatud viis, kuidas need erinevad elemendid omavahel kokku sobivad. Alustame kahe suure maatriksiga A ja B, mida soovite omavahel korrutada. Esiteks jagate need paljudeks väiksemateks alammaatriksiteks või plokkideks, nagu neid mõnikord nimetatakse. Järgmisena saate kasutada Coppersmithi ja Winogradi algoritmi, mis toimib omamoodi juhendina plokkide käsitsemiseks ja lõpuks kokkupanemiseks. "See ütleb mulle, mida korrutada ja mida lisada ning millised kirjed kuhu lähevad" korrutismaatriksis C, ütles Vassilevska Williams. "See on lihtsalt retsept A-st ja B-st C moodustamiseks."

Siiski on konks: mõnikord jõuate plokkideni, millel on ühiseid kirjeid. Nende tootesse jätmine sarnaneks nende kirjete kahekordse loendamisega, nii et mingil hetkel peate vabanema nendest dubleeritud terminitest, mida nimetatakse kattumisteks. Teadlased teevad seda, "tappades" plokid, milles nad asuvad – määrates nende komponendid võrdseks nulliga, et need arvutusest eemaldada.

Siin tulebki lõpuks mängu Strasseni lasermeetod. "Laserimeetod töötab tavaliselt väga hästi ja üldiselt leiab hea viisi plokkide alamhulga hävitamiseks, et kattumine eemaldada, " ütles Le Gall. Pärast seda, kui laser on kõik kattumised kõrvaldanud või "ära põlenud", saate koostada lõpptoote maatriksi C.

Nende erinevate tehnikate kokkupanemise tulemuseks on algoritm kahe maatriksi korrutamiseks üldiselt tahtlikult väikese korrutuste arvuga - vähemalt teoreetiliselt. Lasermeetod ei ole mõeldud praktiliseks; see on lihtsalt viis mõelda ideaalsele viisile maatriksite korrutamiseks. "Me ei kasuta seda meetodit kunagi [arvutis]," ütles Zhou. "Analüüsime seda."

Ja see analüüs viis omega suurima paranemiseni enam kui kümne aasta jooksul.

On leitud kaotus

Duani, Zhou ja Wu eelmise suve paber näitas, et Strasseni protsessi saab siiski märkimisväärselt kiirendada. See kõik oli kontseptsiooni tõttu, mida nad nimetasid varjatud kaotuseks, mis on sügavale varasematesse analüüsidesse maetud – "liiga paljude plokkide tahtmatu tapmise tagajärg," ütles Zhou.

Lasermeetod toimib, märgistades kattuvad plokid prügina, mis on määratud kõrvaldamiseks; teised plokid loetakse vääriliseks ja need salvestatakse. Valikuprotsess on siiski mõnevõrra juhuslik. Prügiks hinnatud plokk võib tegelikult osutuda kasulikuks. See ei olnud täielik üllatus, kuid uurides paljusid neist juhuslikest valikutest, leidis Duani meeskond, et lasermeetod alahindas süstemaatiliselt plokke: rohkem plokke tuleks salvestada ja vähem välja visata. Ja nagu tavaliselt, tähendab vähem jäätmeid suuremat tõhusust.

"Võimalus hoida rohkem plokke ilma kattumiseta viib ... kiirema maatriksi korrutusalgoritmini, " ütles Le Gall.

Pärast selle kaotuse olemasolu tõestamist muutis Duani meeskond plokkide märgistamise lasermeetodil, vähendades oluliselt jäätmeid. Selle tulemusel seadsid nad oomega uueks ülempiiriks umbes 2.371866 - see on paranemine võrreldes eelmise ülempiiriga 2.3728596, seatud 2020. aastal Josh Alman ja Vassilevska Williams. See võib tunduda tagasihoidliku muudatusena, alandades piiri vaid umbes 0.001 võrra. Kuid see on ainus suurim paranemine, mida teadlased on näinud alates 2010. aastast. Võrdluseks, Vassilevska Williamsi ja Almani 2020. aasta tulemus paranes eelkäijaga võrreldes vaid 0.00001 võrra.

Kuid teadlaste jaoks pole kõige põnevam ainult uus rekord ise – mis ei kestnud kaua. See on ka tõsiasi, et paber paljastas uue arengutee, mis seni oli jäänud täiesti märkamatuks. Le Gall ütles, et peaaegu neli aastakümmet on kõik tuginenud samale lasermeetodile. "Siis nad leidsid, et noh, me saame paremini teha."

2024. aasta jaanuari artikkel täpsustas seda uut lähenemisviisi, võimaldades Vassilevska Williamsil, Zhoul ja nende kaasautoritel varjatud kaotust veelgi vähendada. See tõi kaasa oomega ülempiiri täiendava paranemise, vähendades seda 2.371552-ni. Autorid üldistasid seda sama tehnikat ka ristkülikukujuliste (n-kõrval-m) maatriksid — protseduur, millel on rakendusi graafiteoorias, masinõppes ja muudes valdkondades.

Mõned edasised edusammud selles suunas on täiesti kindlad, kuid sellel on piirid. 2015. aastal Le Gall ja kaks kaastöötajat tõestatud et praegune lähenemine – lasermeetod koos Coppersmithi-Winogradi retseptiga – ei saa anda oomega väärtust alla 2.3078. Le Gall ütles, et edasiste täiustuste tegemiseks peate parandama Coppersmithi ja Winogradi algset [lähenemist], mis pole pärast 1987. aastat tegelikult muutunud.. " Kuid seni pole keegi paremat viisi välja mõelnud. Seda ei pruugi isegi olla.

"Oomega parandamine on tegelikult osa selle probleemi mõistmisest, " ütles Zhou. „Kui suudame probleemist hästi aru saada, saame sellele paremaid algoritme välja töötada. [Ja] inimesed on selle igivana probleemi mõistmisega alles väga varajases staadiumis.