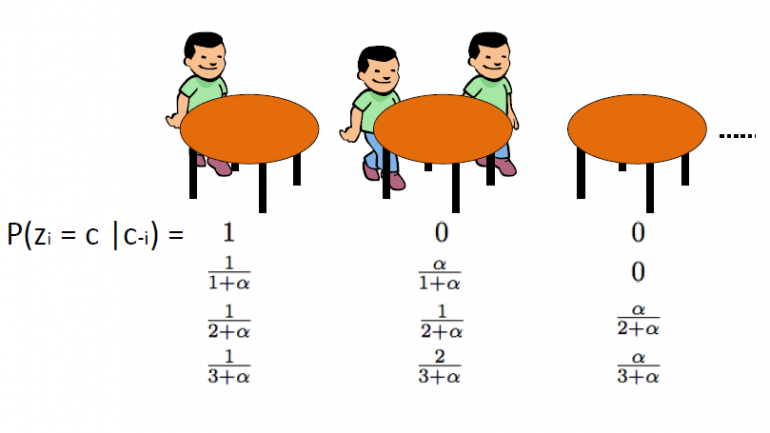Dirichlet töötleb Hiina restorani protsessi ja muid esitusi

• Võib 20 2014
• Vasilis Vryniotis
• . Kommentaarid puuduvad

See artikkel on Dirichleti protsessisegude mudelitega rühmitamist käsitleva sarja kolmas osa. Eelmisel korral määratlesime Dirichleti jaotusel põhineva lõpliku segu mudeli ja esitasime küsimused, kuidas saaksime selle konkreetse mudeli lõpmatuks muuta. Arutasime lühidalt ideed võtta mudeli piir, kui klastrite arv k kipub lõpmatuseni, kuid nagu rõhutasime, ei ole sellise objekti olemasolu triviaalne (teisisõnu, kuidas me tegelikult “võtame mudeli piiri ”?). Tuletame meelde, et põhjus, miks me tahame teha k lõpmatuks, on see, et sel viisil saame mitteparameetrilise mudeli, mis ei nõua andmetes olevate klastrite koguarvu eelmääratlemist.

Värskendus: Datumboxi masinõppe raamistik on nüüd avatud lähtekoodiga ja tasuta lae alla. Tutvuge paketiga com.datumbox.framework.machinelearning.clustering, et näha Dirichleti protsessisegude mudelite rakendamist Javas.

Kuigi meie eesmärk on luua mudel, mis on võimeline andmehulkadel klasterdama, peame enne seda arutama Dirichleti protsesside üle. Pakume nii DP rangeid matemaatilisi määratlusi kui ka intuitiivsemaid selgitusi ning arutame protsessi konstrueerimise viise. Neid konstruktsioone/esitusi võib vaadelda kui võimalust leida Dirichlet' protsessi esinemisi "päris elus".

Hoolimata asjaolust, et püüdsin oma uurimisaruannet kohandada nii, et neid ajaveebi postitusi oleks lihtsam jälgida, on siiski oluline defineerida vajalikud matemaatilised tööriistad ja distributsioonid, enne kui mudelite kasutama hakkame. Dirichlet' protsessi mudelid on aktiivse uurimistöö teema, kuid enne nende kasutamist on vaja statistikat ja stohhastilisi protsesse hästi mõista. Teine probleem on see, et nagu me selles artiklis näeme, saab Dirichleti protsesse esitada/konstrueerida mitmel viisil. Selle tulemusena kasutavad mitmed akadeemilised tööd täiesti erinevat tähistust/konventsioone ja uurivad probleemi erinevatest vaatenurkadest. Selles postituses püüan neid võimalikult lihtsalt selgitada ja kasutada sama tähistust. Loodetavasti saavad asjad selgemaks kahe eelseisva artikliga, mis keskenduvad Dirichleti protsessisegude mudelite määratlusele ja sellele, kuidas neid klastrianalüüsi tegemiseks tegelikult kasutada.

1. Dirichlet' protsessi definitsioon

Dirichleti protsess Θ ruumi kohal on stohhastiline protsess. See on tõenäosusjaotus "tõenäosusjaotuste üle Θ ruumi" ja a sellest joonistamine on diskreetne jaotus. Formaalsemalt on Dirichleti jaotus tõenäosusmõõtude jaotus. A tõenäosusmõõt on ruumi alamhulkade funktsioon Θ kuni [0,1]. G on DP jaotatud juhusliku tõenäosuse mõõt, mida tähistatakse kui , kui mõne partitsiooni jaoks (A₁,…A_n) ruumist Θ meil on see .

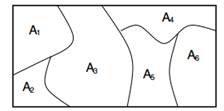
Joonis 1: Piiratud partitsioonide marginaalid on jaotatud Dirichleti järgi.

DP-l on kaks parameetrit: esimene on baasjaotus G₀ mis toimib kui keskmine . Teine on tugevusparameeter α, mis on rangelt positiivne ja toimib nagu pöördvariatsioon . See määrab väljundjaotuse väärtuste kordumise ulatuse. Mida suurem on a väärtus, seda väiksem on kordus; mida väiksem väärtus, seda suurem on väljundjaotuse väärtuste kordus. Lõpuks on ruum Θ parameetriruum, millel me määratleme DP. Lisaks on ruum Θ ka G määratlusruum₀ mis on sama, mis G.

Lihtsam ja rohkem intuitiivne viis Dirichleti protsessi selgitamiseks on järgmine. Oletame, et meil on ruum Θ, mida saab jaotada mis tahes lõplikult (A₁,…,A_n) ja tõenäosusjaotus G, mis määrab neile tõenäosused. G on konkreetne tõenäosusjaotus Θ vahel, kuid on ka palju teisi. Dirichleti protsess Θ-l modelleerib täpselt seda; see on jaotus kõigi võimalike tõenäosusjaotuste üle ruumis Θ. Dirichleti protsess on parameetritega G₀ baasfunktsioon ja α kontsentratsiooni parameeter. Võime öelda, et G jaotub vastavalt DP-le parameetritega α ja G₀ kui G poolt Θ partitsioonidele omistatud tõenäosuste ühisjaotus järgib Dirichleti jaotust. Teise võimalusena võime öelda, et tõenäosused, mille G määrab Θ mis tahes lõplikule partitsioonile, järgivad Dirichleti jaotust.

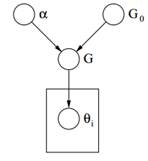
Joonis 2: Dirichlet' protsessi graafiline mudel

Lõpuks näeme ülalpool DP graafiline mudel. Peaksime märkima, et α on skalaarne hüperparameeter, G₀ on DP baasjaotus, G juhuslik jaotus Θ parameetriruumis, mis on võetud DP-st, mis määrab parameetritele tõenäosused ja θ_i on parameetrivektor, mis on tõmmatud G jaotusest ja on Θ ruumi element.

2. Tagumised Dirichlet protsessid

Tagumise Dirichlet protsesside üle arutasid Ferguson. Alustuseks joonistame Dirichleti protsessist juhusliku tõenäosuse mõõdiku G, . Kuna G on tõenäosusjaotus üle Θ, saame ka sellest jaotusest valimi võtta ja koostada sõltumatud identse jaotusega valimid θ₁,…, θ_n ~ G. Kuna Dirichleti protsessi joonised on diskreetsed jaotused, saame esitada kus on lühike märge jaoks mis on deltafunktsioon, mis võtab 1 kui ja 0 mujal. Selle huvitav efekt on see, et kuna G on nii defineeritud, on positiivne tõenäosus, et erinevatel valimitel on sama väärtus . Nagu hiljem näeme, loob see klastriefekti, mida saab kasutada andmekogumite klastrianalüüsi tegemiseks.

Kasutades ülaltoodud definitsioone ja tähelepanekuid, tahame hinnata Dirichlet' protsessi tagantjärele näidistega θ. Sellest hoolimata, kuna me seda teame ja kasutades Bayesi reegleid ja konjugaati Dirichleti ja Multinomiaali vahel, saame selle ja .

1. võrrand: tagumine Dirichlet' protsess

See omadus on väga oluline ja seda kasutavad erinevad DP esindused.

3. Dirichlet Protsessi esitused

Eelmistes segmentides defineerisime Dirichlet' protsessi ja esitasime selle teoreetilise mudeli. Üks oluline küsimus, millele peame vastama, on see, kuidas me teame, et selline objekt on olemas ja kuidas me saame konstrueerida ja esindada Dirichlet' protsess.

Esimesed märgid olemasolust andsid Ferguson kes kasutas Kolmogorovi konsistentsi teoreemi, andis Dirichlet' protsessi definitsiooni ja kirjeldas tagumist Dirichlet' protsessi. Oma uurimistööd jätkates, Blackwell ja MacQueen kasutas de Finetti teoreemi, et tõestada sellise juhusliku tõenäosuse mõõtme olemasolu ja tutvustas Blackwell-MacQueeni urni skeemi, mis rahuldab Dirichlet' protsessi omadusi. 1994. aastal Sethuraman pakkus täiendava lihtsa ja otsese viisi DP konstrueerimiseks, võttes kasutusele pulgamurdva konstruktsiooni. Lõpuks esitati veel üks esindus Aldous kes tutvustas Hiina restoraniprotsessi kui tõhusat viisi Dirichleti protsessi konstrueerimiseks.

Dirichlet' protsessi erinevad esitused on matemaatiliselt samaväärsed, kuid nende sõnastus on erinev, kuna nad uurivad probleemi erinevatest vaatenurkadest. Allpool tutvustame kirjanduses leiduvaid levinumaid esitusi ja keskendume Hiina restoraniprotsessile, mis pakub lihtsat ja arvutuslikult tõhusat viisi Dirichleti protsessi järeldusalgoritmide koostamiseks.

3.1 Blackwell-MacQueeni urniskeem

Blackwell-MacQueeni urni skeemi saab kasutada Dirichleti protsessi esindamiseks ja selle tutvustas Blackwell ja MacQueen. See põhineb Pólya urniskeemil, mida võib vaadelda kui vastupidist proovide võtmise mudelit ilma asendamiseta. Pólya urniskeemis eeldame, et meil on läbipaistmatu urn, mis sisaldab värvilisi palle, ja me joonistame pallid juhuslikult. Palli joonistades jälgime selle värvi, paneme selle tagasi urni ja lisame sama värvi palli juurde. Sarnast skeemi kasutavad Blackwell ja MacQueen Dirichleti protsessi konstrueerimiseks.

See skeem loob θ jada₁,θ₂,… koos tingimuslikud tõenäosused . Selles skeemis eeldame, et G₀ on jaotus värvide ja iga θ vahel_n tähistab urni asetatud palli värvi. The algoritm on järgmine:

· Alustame tühja urniga.

· Tõenäosusega võrdeline α joonistame ja lisame urni seda värvi palli.

· Tõenäosusega, mis on võrdeline n-1-ga, tõmbame urnist juhusliku palli, jälgime selle värvi, asetame selle tagasi urni ja lisame urni sama värvi palli.

Varem alustasime Dirichleti protsessiga ja tuletasime Blackwell-MacQueeni skeemi. Nüüd alustame vastupidiselt Blackwell-MacQueeni skeemist ja tuletame DP. Alates θ_i on tõmmatud G-st iid viisil, on nende ühine jaotus mis tahes lõplike permutatsioonide suhtes muutumatu ja seega on need vahetatavad. Järelikult, kasutades de Finetti teoreemi, saame, et nende identseks muutmiseks peab eksisteerima jaotus mõõtude vahel ja see jaotus on Dirichlet' protsess. Selle tulemusena tõestame, et Blackwell-MacQueeni urniskeem kujutab endast DP-d ja see annab meile konkreetse viisi selle konstrueerimiseks. Nagu hiljem näeme, on see skeem matemaatiliselt samaväärne Hiina restoraniprotsessiga.

3.2 Pulka murdev konstruktsioon

Pulga murdev konstruktsioon on alternatiivne viis Dirichlet protsessi esindamiseks, mille tutvustas Sethuraman. See on konstruktiivne viis selle moodustamiseks levitamine ja kasutab järgides analoogiat: Eeldame, et meil on pulk pikkusega 1, murrame selle positsioonis β₁ ja omistame π₁ võrdne murdunud pulgaosa pikkusega. Kordame sama protsessi, et saada π₂, π₃,… jne; selle skeemi defineerimise viisi tõttu saame seda jätkata lõpmatuseni.

Ülaltoodu põhjal on π_k saab modelleerida kui , Kus samas kui nagu eelmistes skeemides, valitakse θ otse baasjaotuse järgi . Järelikult saab G jaotuse kirjutada π-ga kaalutud deltafunktsioonide summana_k tõenäosus, mis on võrdne . Seega annab pulgamurdev konstruktsioon meile lihtsa ja intuitiivse viisi Dirichleti protsessi konstrueerimiseks.

3.3 Hiina restorani protsess

Hiina restoraniprotsess, mille tutvustas Aldous, on veel üks tõhus viis Dirichleti protsessi esindamiseks ja seda saab otse siduda Blackwell-MacQueeni urniskeemiga. See skeem kasutab järgides analoogiat: Eeldame, et seal on Hiina restoran, kus on lõpmatult palju laudu. Kui kliendid restorani sisenevad, istuvad nad juhuslikult mõne hõivatud laua juurde või otsustavad nad istuda esimese vaba laua juurde.

CRP määrab positiivsete täisarvude jaotuse partitsioonide ruumis. Alustame θ joonistamisega₁,…θ_n Blackwell-MacQueeni urniskeemist. Nagu eelmistes segmentides arutasime, ootame klastriefekti ja seega on ainulaadsete θ väärtuste koguarv k oluliselt väiksem kui n. Seega määrab see hulga {1,2,…,n} partitsiooni k klastris. Järelikult indutseerib Blackwell-MacQueeni urniskeemist joonistamine komplekti {1,2,…,n} juhusliku partitsiooni. Hiina restoraniprotsess on sellest tingitud jaotus vaheseinte vahel. Algoritm on järgmine:

· Alustame tühja restoraniga.

· 1^st klient istub alati 1^st tabel

· N+1^th kliendil on 2 võimalust:

o Istuge tõenäoliselt esimesele vabale lauale

o Istuge suure tõenäosusega mis tahes k-ndale hõivatud lauale
kus on sellel laual istujate arv

Kus α on DP hajuvusväärtus ja n on restoranis teatud ajahetkel viibivate klientide koguarv. Varjatud muutuja z_i salvestab i tabelinumbri^th klient ja võtab väärtused 1-st k-ni_n kus k_n on hõivatud laudade koguarv, kui restoranis on n klienti. Peame märkima, et k_n on alati väiksem või võrdne n-ga ja keskmiselt on see umbes . Lõpuks peaksime märkima, et tabeli paigutuse tõenäosus on permutatsioonide suhtes muutumatu. Seega z_i on vahetatav, mis tähendab, et sama suure klientide arvuga tabelitel on sama tõenäosus.

Hiina restoraniprotsess on tugevalt seotud Pólya urniskeemiga ja Dirichleti protsessiga. CRP on viis määrata a jaotus vaheseinte vahel (tabeliülesanded) n punktist ja seda saab kasutada latentse muutuja z ruumi priorina_i mis määrab klastri ülesanded. CRP on samaväärne Pólya urniskeemiga, ainult selle erinevusega, et see ei määra igale tabelile/klastrile parameetreid. Minema CRP-st Pólya urniskeemile joonistame kõigi tabelite jaoks k=1,2… ja seejärel iga x jaoks_i mis on rühmitatud tabelisse z_i määrama a . Teisisõnu määrake uuele x-ile_i tabeli parameeter θ. Lõpuks sellest ajast me ei saa määrata θ lõpmatutele tabelitele algusest peale, saame lihtsalt määrata uue θ iga kord, kui keegi uuele lauale istub. Kõigest eelnevast tulenevalt võib CRP aidata meil koostada arvutuslikult tõhusaid algoritme andmekogumite klastrianalüüsi tegemiseks.

Selles postituses arutasime Dirichleti protsessi ja selle loomise mitmeid viise. Kasutame ülaltoodud ideid järgmises artiklis. Tutvustame Dirichleti protsessi segumudelit ja kasutame Hiina restoranide esindust Dirichleti protsessi koostamiseks ja tooriku klastri analüüsiks. Kui jätsite mõne punkti vahele, ärge muretsege, sest kahe järgmise artikliga hakkavad asjad selgemaks muutuma.

Loodan, et see postitus oli teile huvitav. Kui jagasite seda Facebookis ja Twitteris, leidke hetk. 🙂