Big O-merkintä ja algoritmianalyysi Python-esimerkeillä

esittely

On yleensä useita tapoja ratkaista ongelma käyttämällä tietokoneohjelmaa. On esimerkiksi useita tapoja lajitella kohteita taulukossa – voit käyttää Yhdistä lajittelu, kupla, lisäyslaji, ja niin edelleen. Kaikilla näillä algoritmeilla on omat hyvät ja huonot puolensa, ja kehittäjän tehtävänä on punnita niitä voidakseen valita parhaan algoritmin käytettäväksi kaikissa käyttötapauksissa. Toisin sanoen pääkysymys on, mitä algoritmia käytetään tietyn ongelman ratkaisemiseen, kun ongelmaan on useita ratkaisuja.

Algoritmianalyysi viittaa eri algoritmien monimutkaisuuden analysointiin ja tehokkaimman algoritmin löytämiseen käsillä olevan ongelman ratkaisemiseksi. Big-O-merkintä on tilastollinen mitta, jota käytetään kuvaamaan algoritmin monimutkaisuutta.

Tässä oppaassa teemme ensin lyhyen katsauksen algoritmianalyysiin ja sitten tarkastelemme syvällisemmin Big-O-merkintää. Katsotaan, kuinka Big-O-merkinnän avulla voidaan löytää algoritmin monimutkaisuus eri Python-funktioiden avulla.

Miksi algoritmianalyysi on tärkeä?

Ymmärtääksemme, miksi algoritmianalyysi on tärkeää, otamme avuksi yksinkertaisen esimerkin. Oletetaan, että esimies antaa kahdelle työntekijälleen tehtävän suunnitella Pythonissa algoritmi, joka laskee käyttäjän syöttämän luvun kertoimen. Ensimmäisen työntekijän kehittämä algoritmi näyttää tältä:

def fact(n):
    product = 1
    for i in range(n):
        product = product * (i+1)
    return product

print(fact(5))

Huomaa, että algoritmi yksinkertaisesti ottaa kokonaisluvun argumenttina. Sisällä fact() funktio nimeltä muuttuja product on alustettu 1. Silmukka suoritetaan alkaen 1 että n ja jokaisen iteraation aikana arvon product kerrotaan silmukan iteroimalla luvulla ja tulos tallennetaan product taas muuttuja. Kun silmukka on suoritettu, product muuttuja sisältää faktoriaalin.

Vastaavasti toinen työntekijä kehitti algoritmin, joka laskee luvun kertoimen. Toinen työntekijä käytti rekursiivista funktiota luvun kertoimen laskemiseen n:

def fact2(n):
    if n == 0:
        return 1
    else:
        return n * fact2(n-1)

print(fact2(5))

Esimiehen on päätettävä, mitä algoritmia käyttää. Tätä varten he ovat päättäneet valita, mikä algoritmi toimii nopeammin. Yksi tapa tehdä niin on löytää aika, joka tarvitaan koodin suorittamiseen samassa syötteessä.

Jupyter-muistikirjassa voit käyttää %timeit kirjaimellinen, jota seuraa funktiokutsu, jotta saadaan selville funktion suorittamiseen kulunut aika:

%timeit fact(50)

Tämä antaa meille:

9 µs ± 405 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Lähtö sanoo, että algoritmi kestää 9 mikrosekuntia (plus/miinus 45 nanosekuntia) per silmukka.

Samalla tavalla voimme laskea, kuinka paljon aikaa toisen lähestymistavan suorittaminen vie:

%timeit fact2(50)

Tämä johtaa:

15.7 µs ± 427 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Toinen algoritmi, joka sisältää rekursion kestää 15 mikrosekuntia (plus/miinus 427 nanosekuntia).

Suoritusaika osoittaa, että ensimmäinen algoritmi on nopeampi verrattuna toiseen algoritmiin, johon liittyy rekursio. Suuria panoksia käytettäessä suorituskykyeroista voi tulla merkittävämpi.

Suoritusaika ei kuitenkaan ole hyvä mittari algoritmin monimutkaisuuden mittaamiseen, koska se riippuu laitteistosta. Algoritmille tarvitaan objektiivisempi kompleksisuusanalyysimetriikka. Tässä on Iso O-merkintä tulee pelaamaan.

Algoritmianalyysi Big-O-merkinnällä

Big-O-merkintä tarkoittaa suhdetta algoritmin syötteen ja algoritmin suorittamiseen tarvittavien vaiheiden välillä. Sitä merkitään isolla O-kirjaimella, jota seuraa avaava ja sulkeva sulkumerkki. Sulkujen sisällä syötteen ja algoritmin suorittamien vaiheiden välinen suhde esitetään käyttämällä "n":tä.

Tärkeintä on – Big-O ei ole kiinnostunut a erityinen esimerkki, jossa suoritat algoritmia, kuten fact(50), vaan pikemminkin kuinka hyvin se toimii asteikko annettu kasvava panos. Tämä on paljon parempi mittari arvioinnissa kuin konkreettinen aika konkreettiselle tapaukselle!

Esimerkiksi jos on a lineaarinen suhde syötteen ja algoritmin suorittaman suoritusvaiheen välillä käytetty Big-O-merkintä on O (n). Vastaavasti Big-O-merkintä for neliöfunktiot is O(n²).

Intuition rakentaminen:

• O (n): klo n=1, 1 askel on otettu. klo n=10, otetaan 10 askelta.
• O(n²): klo n=1, 1 askel on otettu. klo n=10, otetaan 100 askelta.

At n=1, nämä kaksi toimisivat samalla tavalla! Tämä on toinen syy siihen, miksi syötteen ja syötteen käsittelyvaiheiden välisen suhteen tarkkaileminen on parempi kuin pelkkä funktioiden arviointi konkreettisella syötteellä.

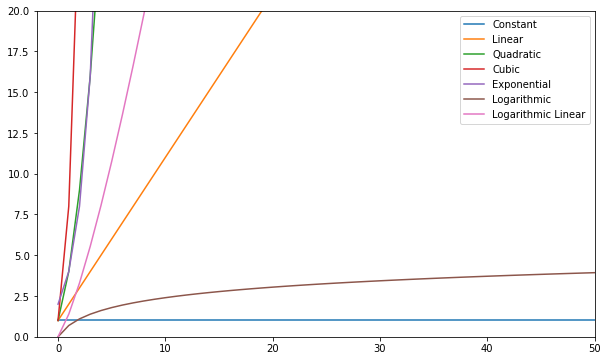
Seuraavassa on joitain yleisimmistä Big-O-toiminnoista:

Nimi	Iso O
Vakio	O (c)
Lineaarinen	O (n)
neliöllinen	O(n²)
kuutio-	O(n³)
Räjähdysmäinen	O(2)
Logaritminen	O (log (n))
Log Lineaarinen	O(nlog(n))

Voit visualisoida nämä toiminnot ja verrata niitä:

Yleisesti ottaen kaikkea lineaarista pahempaa pidetään huonona kompleksina (eli tehottomana) ja sitä tulisi välttää, jos mahdollista. Lineaarinen monimutkaisuus on ok ja yleensä välttämätön paha. Logaritminen on hyvä. Constant on hämmästyttävää!

Saadaksesi käsityksen siitä, kuinka Big-O lasketaan, katsotaanpa joitain esimerkkejä vakiosta, lineaarisesta ja neliöllisestä monimutkaisuudesta.

Jatkuva monimutkaisuus - O(C)

Algoritmin monimutkaisuuden sanotaan olevan vakio, jos algoritmin suorittamiseen vaadittavat vaiheet pysyvät vakioina syötteiden lukumäärästä riippumatta. Jatkuva monimutkaisuus on merkitty O (c) jossa c voi olla mikä tahansa vakioluku.

Kirjoita Pythonissa yksinkertainen algoritmi, joka löytää luettelon ensimmäisen kohteen neliön ja tulostaa sen sitten näytölle:

def constant_algo(items):
    result = items[0] * items[0]
    print(result)

constant_algo([4, 5, 6, 8])

Yllä olevassa käsikirjoituksessa syötteen koosta riippumatta, tai syöttöluettelon kohteiden määrä items, algoritmi suorittaa vain 2 vaihetta:

1. Ensimmäisen elementin neliön löytäminen
2. Tulosta tulos näytölle.

Siksi monimutkaisuus pysyy vakiona.

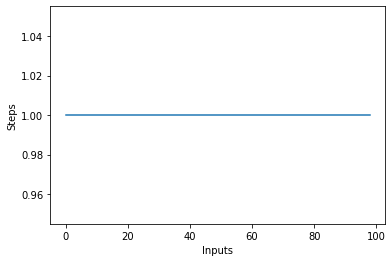
Jos piirrät viivakuvaajan, jonka koko vaihtelee items syöttämällä X-akselilla ja askelmäärän Y-akselilla, saat suoran viivan. Luodaan lyhyt käsikirjoitus, joka auttaa meitä visualisoimaan tämän. Riippumatta syötteiden määrästä, suoritettujen vaiheiden määrä pysyy samana:

steps = []
def constant(n):
    return 1
    
for i in range(1, 100):
    steps.append(constant(i))
plt.plot(steps)

Lineaarinen monimutkaisuus - O (n)

Algoritmin monimutkaisuuden sanotaan olevan lineaarinen, jos algoritmin suorittamiseen tarvittavat vaiheet kasvavat tai vähenevät lineaarisesti syötteiden lukumäärän mukaan. Lineaarinen monimutkaisuus on merkitty O (n).

Tässä esimerkissä kirjoitetaan yksinkertainen ohjelma, joka näyttää kaikki luettelon kohteet konsoliin:

def linear_algo(items):
    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Monimutkaisuus linear_algo() funktio on lineaarinen yllä olevassa esimerkissä, koska for-silmukan iteraatioiden määrä on yhtä suuri kuin tulon koko items ryhmä. Esimerkiksi, jos siinä on 4 kohdetta items luettelossa, for-silmukka suoritetaan 4 kertaa.

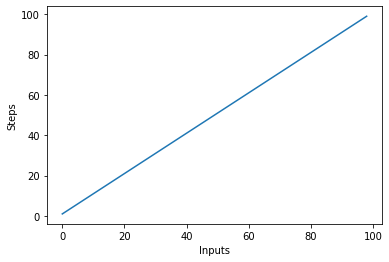
Luodaan nopeasti käyrä lineaarisen kompleksisuuden algoritmille syötteiden lukumäärällä x-akselilla ja askelmäärällä y-akselilla:

steps = []
def linear(n):
    return n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

Tämä johtaa:

Tärkeä asia on huomata, että suurilla syötteillä vakioilla on taipumus menettää arvoaan. Tästä syystä tyypillisesti poistamme vakiot Big-O-merkinnöistä, ja lauseke, kuten O(2n), lyhennetään yleensä O(n):ksi. Sekä O(2n) että O(n) ovat lineaarisia – lineaarinen suhde ratkaisee, ei konkreettinen arvo. Muokataan esimerkiksi linear_algo():

def linear_algo(items):
    for item in items:
        print(item)

    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

On kaksi for-silmukkaa, jotka toistuvat tulon yli items lista. Siksi algoritmin monimutkaisuus muuttuu O (2n), kuitenkin syöttöluettelon äärettömien kohteiden tapauksessa äärettömän kahdesti on silti yhtä suuri kuin ääretön. Voimme jättää huomioimatta vakion 2 (koska se on lopulta merkityksetön) ja algoritmin monimutkaisuus säilyy O (n).

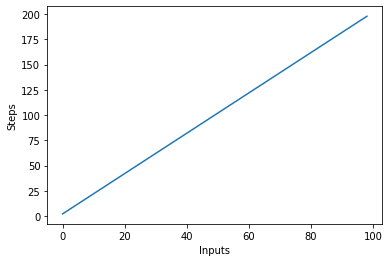
Visualisoidaan tämä uusi algoritmi piirtämällä syötteet X-akselille ja vaiheiden lukumäärä Y-akselille:

steps = []
def linear(n):
    return 2*n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

Yllä olevasta käsikirjoituksesta näet sen selvästi y = 2ntulos on kuitenkin lineaarinen ja näyttää tältä:

Neliöllinen monimutkaisuus - O(n²)

Algoritmin monimutkaisuuden sanotaan olevan neliöllinen, kun algoritmin suorittamiseen tarvittavat vaiheet ovat syötteessä olevien kohteiden lukumäärän neliöfunktio. Neliön monimutkaisuus on merkitty nimellä O(n²):

def quadratic_algo(items):
    for item in items:
        for item2 in items:
            print(item, ' ' ,item2)

quadratic_algo([4, 5, 6, 8])

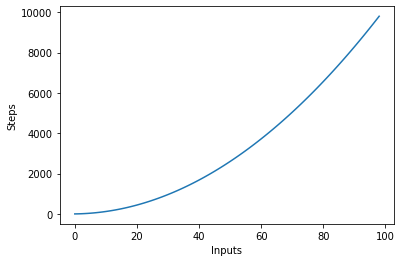
Meillä on ulompi silmukka, joka toistuu kaikkien syöttöluettelon kohteiden läpi, ja sitten sisäkkäinen sisäsilmukka, joka iteroituu jälleen kaikkien syöteluettelon kohteiden läpi. Suoritettujen vaiheiden kokonaismäärä on n*n, missä n on syöttötaulukon kohteiden lukumäärä.

Seuraavassa kaaviossa esitetään syötteiden määrä vaiheiden funktiona neliöllisen monimutkaisuuden omaavalle algoritmille:

Logaritminen monimutkaisuus - O (kirjaudu)

Jotkut algoritmit saavuttavat logaritmisen monimutkaisuuden, kuten Binaarihaku. Binaarihaku etsii elementtiä taulukosta valitsemalla keskimmäinen taulukosta ja karsimalla sen puolikkaan, jossa elementtiä ei ole. Se tekee tämän uudelleen jäljellä olevan puolikkaan ajan ja jatkaa samoja vaiheita, kunnes elementti löytyy. Jokaisessa vaiheessa se puolikkaat taulukon elementtien lukumäärä.

Tämä edellyttää, että matriisi on lajiteltu, ja meidän on tehtävä oletus tiedoista (kuten se, että se on lajiteltu).

Kun voit tehdä oletuksia saapuvista tiedoista, voit ryhtyä toimiin, jotka vähentävät algoritmin monimutkaisuutta. Logaritminen monimutkaisuus on toivottavaa, koska sillä saavutetaan hyvä suorituskyky jopa erittäin skaalatulla syötteellä.

Monimutkaisten funktioiden monimutkaisuuden löytäminen?

Aiemmissa esimerkeissä syötteessämme oli melko yksinkertaisia ​​toimintoja. Mutta kuinka laskemme funktioiden Big-O, jotka kutsuvat (useita) muita toimintoja syötteestä?

Katsotaanpa:

def complex_algo(items):

    for i in range(5):
        print("Python is awesome")

    for item in items:
        print(item)

    for item in items:
        print(item)

    print("Big O")
    print("Big O")
    print("Big O")

complex_algo([4, 5, 6, 8])

Yllä olevassa skriptissä suoritetaan useita tehtäviä, ensin merkkijono tulostetaan 5 kertaa konsolissa käyttämällä print lausunto. Seuraavaksi tulostamme syöttöluettelon kahdesti näytölle ja lopuksi toinen merkkijono tulostetaan kolme kertaa konsolissa. Sellaisen algoritmin monimutkaisuuden selvittämiseksi meidän on jaettava algoritmikoodi osiin ja yritettävä löytää yksittäisten osien monimutkaisuus. Merkitse muistiin jokaisen kappaleen monimutkaisuus.

Ensimmäisessä osiossa meillä on:

for i in range(5):
	print("Python is awesome")

Tämän osan monimutkaisuus on O (5) koska tässä koodissa suoritetaan viisi vakiovaihetta syötteestä riippumatta.

Seuraavaksi meillä on:

for item in items:
	print(item)

Tiedämme yllä olevan koodin monimutkaisuuden O (n). Samoin seuraavan koodin monimutkaisuus on myös O (n):

for item in items:
	print(item)

Lopuksi seuraavassa koodinpätkässä merkkijono tulostetaan kolme kertaa, joten monimutkaisuus on O (3):

print("Big O")
print("Big O")
print("Big O")

Yleisen monimutkaisuuden löytämiseksi meidän on yksinkertaisesti lisättävä nämä yksittäiset monimutkaisuudet:

O(5) + O(n) + O(n) + O(3)

Yllä olevaa yksinkertaistamalla saamme:

O(8) + O(2n) = O(8+2n)

Sanoimme aiemmin, että kun syötteestä (jonka tässä tapauksessa pituus on n) tulee äärimmäisen suuri, muuttuvat vakiot merkityksettömiksi eli kaksi kertaa tai puolet äärettömyydestä jää silti äärettömäksi. Siksi voimme jättää huomioimatta vakiot. Algoritmin lopullinen monimutkaisuus on O (n)!

Huonoin vs paras tapauksen monimutkaisuus

Yleensä, kun joku kysyy sinulta algoritmin monimutkaisuutta – hän on kiinnostunut pahimman mahdollisen monimutkaisuudesta (Big-O). Joskus he saattavat olla kiinnostuneita myös parhaan tapauksen monimutkaisuudesta (Big-Omega).

Ymmärtääksemme näiden välisen suhteen, katsotaanpa toista koodinpätkää:

def search_algo(num, items):
    for item in items:
        if item == num:
            return True
        else:
            pass
nums = [2, 4, 6, 8, 10]

print(search_algo(2, nums))

Yllä olevassa skriptissä meillä on toiminto, joka syöttää numeron ja numeroluettelon. Se palauttaa tosi, jos välitetty numero löytyy numeroluettelosta, muussa tapauksessa se palauttaa None. Jos haet luettelosta 2, se löytyy ensimmäisestä vertailusta. Tämä on algoritmin parhaassa tapauksessa monimutkaisuus siinä mielessä, että etsitty kohde löytyy ensimmäisestä hatusta hakemistosta. Paras tapauksen monimutkaisuus, tässä tapauksessa on O (1). Toisaalta, jos haet 10, se löytyy viimeksi haetuista hakemistoista. Algoritmin on siis etsittävä kaikki luettelon kohteet pahimman tapauksen monimutkaisuus tulee O (n).

Parhaan ja pahimman tapauksen monimutkaisuuden lisäksi voit myös laskea keskimääräinen monimutkaisuus (Big-Theta) algoritmista, joka kertoo "mikä on algoritmin odotettu aikamonimutkaisuus satunnaisella syötteellä"?

Avaruuden monimutkaisuus

Ajan monimutkaisuuden lisäksi, jossa lasket algoritmin suorittamiseen tarvittavien vaiheiden määrän, löydät myös tilan monimutkaisuus joka viittaa tilan määrään, joka sinun on varattava muistista ohjelman suorittamisen aikana.

Katso seuraava esimerkki:

def return_squares(n):
    square_list = []
    for num in n:
        square_list.append(num * num)

    return square_list

nums = [2, 4, 6, 8, 10]
print(return_squares(nums))

- return_squares() funktio hyväksyy kokonaislukuluettelon ja palauttaa luettelon vastaavilla neliöillä. Algoritmin on varattava muistia samalle määrälle kohteita kuin syöttöluettelossa. Siksi algoritmin tilamonimutkaisuus muuttuu O (n).

Yhteenveto

Big-O-merkintä on vakiomittari, jota käytetään algoritmin monimutkaisuuden mittaamiseen. Tässä oppaassa tutkimme, mitä Big-O-merkintä on ja miten sitä voidaan käyttää useiden algoritmien monimutkaisuuden mittaamiseen. Tutkimme myös erilaisia ​​Big-O-funktioita erilaisten Python-esimerkkien avulla. Lopuksi tarkastelimme lyhyesti pahimman ja parhaan tapauksen monimutkaisuutta sekä tilan monimutkaisuutta.