Kvanttidynamiikan mittarikuva

Kvanttidynamiikan mittarikuva

Aikaleima: 21. maaliskuuta 2024 6

Kevin Slagle

Sähkö- ja tietokonetekniikan laitos, Rice University, Houston, Texas 77005 USA
Fysiikan laitos, California Institute of Technology, Pasadena, California 91125, USA
Institute for Quantum Information and Matter ja Walter Burke Institute for Theoretical Physics, California Institute of Technology, Pasadena, California 91125, USA

Onko tämä artikkeli mielenkiintoinen vai haluatko keskustella? Scite tai jätä kommentti SciRate.

Abstrakti

Vaikka paikalliset hamiltonilaiset osoittavat paikallista aikadynamiikkaa, tämä paikka ei ole selkeä Schrödinger-kuvassa siinä mielessä, että aaltofunktion amplitudit eivät tottele paikallista liikeyhtälöä. Osoitamme, että geometrinen paikallisuus voidaan saavuttaa eksplisiittisesti liikeyhtälöissä "mittaamalla" kvanttimekaniikan globaali unitaarinen invarianssi paikalliseksi mittariinvarianssiksi. Toisin sanoen odotusarvot $langle psi|A|psi range$ ovat invariantteja globaalissa unitaarisessa muunnoksessa, joka vaikuttaa aaltofunktioon $|psirangle - U |psirangle$ ja operaattorit $A - UAU^dagger$, ja osoitamme, että se on mahdollista mittaamaan tämän globaalin invarianssin paikalliseksi invarianssiksi. Tätä varten korvaamme aaltofunktion joukolla paikallisia aaltofunktioita $|psi_Jrangle$, yksi kutakin tilan $J$ paikkaa kohden. Tilapäisten tilkkujen kokoelma valitaan peittämään tilaa; esim. voisimme valita paikat yksittäisiksi kubitiksi tai lähimpien naapuripaikkojen hilassa. Paikalliset aaltofunktiot, jotka liittyvät vierekkäisiin spatiaalisten paikkojen $I$ ja $J$ pareihin, liittyvät toisiinsa dynaamisilla unitaarisilla muunnoksilla $U_{IJ}$. Paikalliset aaltofunktiot ovat paikallisia siinä mielessä, että niiden dynamiikka on paikallista. Toisin sanoen paikallisten aaltofunktioiden $|psi_Jrangle$ ja yhteyksien $U_{IJ}$ liikeyhtälöt ovat eksplisiittisesti paikallisia avaruudessa ja riippuvat vain lähellä olevista Hamiltonin termeistä. (Paikalliset aaltofunktiot ovat monen kappaleen aaltofunktioita ja niillä on sama Hilbert-avaruusulottuvuus kuin tavallisella aaltofunktiolla.) Kutsumme tätä kvanttidynamiikan kuvaa mittarikuvaksi, koska siinä on paikallinen mittarin invarianssi. Yksittäisen spatiaalisen pisteen paikallinen dynamiikka liittyy vuorovaikutuskuvaan, jossa vuorovaikutus Hamiltonin koostuu vain läheisistä Hamiltonin termeistä. Voimme myös yleistää eksplisiittisen lokaisuuden sisällyttämällä paikallisuuden paikallisvarauksiin ja energiatiheyksiin.

Mittarikuva Quantum Dynamics PlatoBlockchain Data Intelligencesta. Pystysuuntainen haku. Ai.

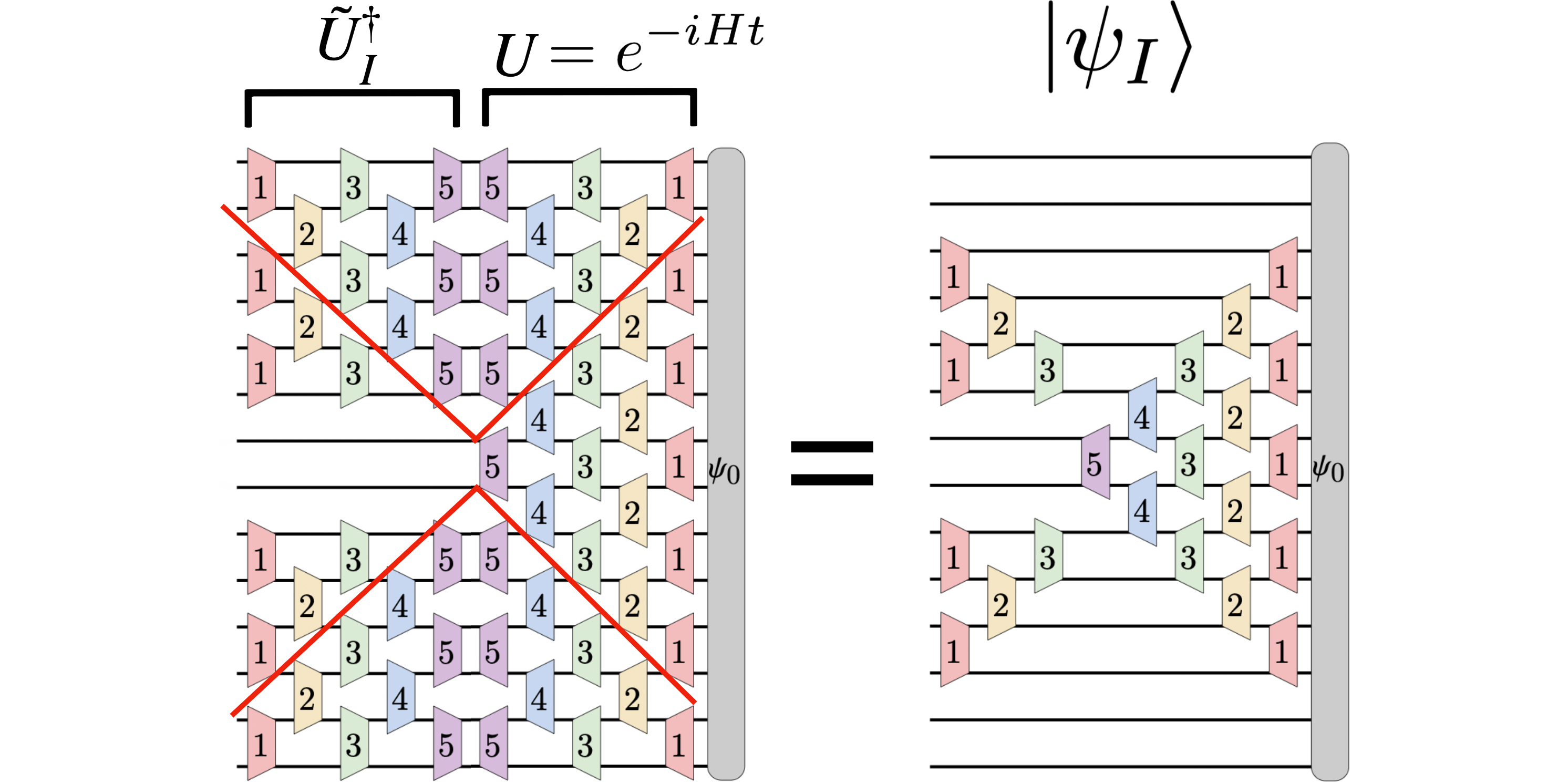
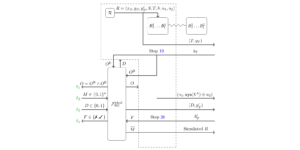
Suositeltu kuva: Schrodingerin kuvassa alkuperäinen aaltofunktio $|psi_0rangle$ kehittyy $U(t) |psi_0rangle$ ajan $t$ jälkeen, missä $U(t) = e^{-iHt}$ on unitaarinen aikaevoluutio operaattori. Sen sijaan mittarikuvassa otetaan huomioon paikalliset aaltofunktiot $|psi_I(t)rangle$, jotka liittyvät avaruudessa olevaan osajoukkoon (tai paikkakuntaan) $I$. Aika kehittynyt paikallinen aaltofunktio $|psi_I(t)rangle = tilde{U}_I^dagger(t) |psi(t)rangle$ saadaan Schrodingerin aaltofunktiosta $|psi(t)rangle = U(t) |psi_0rangle $ unitaarioperaattorilla $tilde{U}_I^dagger(t)$, joka kääntää ajan kehityksen päinvastaiseksi alueen $I$ ulkopuolella. Tämän seurauksena paikallinen aaltofunktion dynamiikka $partial_I |psi_I(t)rangle$ riippuu vain lähellä olevista Hamiltonin termeistä, jotka menevät päällekkäin alueen $I$ kanssa. Kuvassa nämä unitaarioperaattorit ovat kvanttipiirejä ja osoitetaan, että suuri osa ajasta $U(t)$ tapahtuva kehitys kumoutuu $tilde{U}_I^dagger(t)$, jolloin jäljelle jää vain tiimalasin muotoinen ajan evoluutiooperaattori vaikuttavat alkuperäiseen aaltofunktioon (kuvan oikealla puolella). Tämä tiimalasin muotoinen operaattori on analoginen Heisenbergin kuvan valokartion muotoisen operaattorin kasvun kanssa.

Suosittu yhteenveto

Kaksi tunnetuinta kvanttidynamiikan kuvaa ovat Schrodingerin ja Heisenbergin kuvat. Schrodingerin kuvassa aaltofunktio kehittyy ajassa, kun taas Heisenbergin kuvassa aaltofunktio on vakio, mutta operaattorit kehittyvät ajassa. Tässä työssä esittelemme uuden kuvan kvanttidynamiikasta, mittarikuvasta, joka muodostaa syvät yhteydet tiedon paikkakuntaan ja mittariteoriaan.

Mitä tulee paikallisuuteen: Heisenbergin kuvan hyvä etu on, että paikallisuus on eksplisiittinen liikeyhtälöissä. Toisin sanoen paikallisen operaattorin ajan kehitys riippuu vain lähellä olevien paikallisten toimijoiden tilasta. Sitä vastoin lokaliteetti ei ole tällä tavalla eksplisiittinen Schrodingerin kuvassa, jolle on olemassa yksi aaltofunktio, jonka aikadynamiikka riippuu operaattoreista kaikkialla avaruudessa. Uusi mittarikuvamme muokkaa Schrodingerin kuvaa siten, että voimme laskea "paikallisen aaltofunktion", joka kuljettaa samaa tietoa kuin Schrodingerin aaltofunktio, oletetaan, että paikallisten aaltofunktioiden aikadynamiikka mittarikuvassa riippuu vain lähistöllä olevista Hamiltonin termeistä, mikä tekee lokaisuuden eksplisiittiseksi liikeyhtälöt. Tämän eksplisiittisen paikallisuuden saavuttamiseksi mittarikuva lisää mittarikenttiä liikeyhtälöihin.

Mittariteoria luo syvän yhteyden globaalin symmetrian Hamiltonin (tai Lagrangin) ja toisen Hamiltonin välillä, jossa globaali symmetria korvataan paikallisella mittarin symmetrialla dynaamisten mittarikenttien avulla. Mielenkiintoista on, että Schrodingerin yhtälö $ihbar partial_t |psirangle = H |psirangle$ hyväksyy globaalin unitaariinvarianssin, joka saadaan muunnoksella $|psirangle U |psirangle$ ja $H UHU^dagger$. Työmme osoittaa, että tähän Schrodingerin yhtälön globaaliin invarianssiin on mahdollista soveltaa mittariteoriaa myös uuden liikeyhtälön, eli mittarikuvan, saamiseksi dynaamisilla mittarikentillä ja paikallisen ulottuman invarianssilla.

► BibTeX-tiedot

► Viitteet

[1] David Deutsch ja Patrick Hayden. "Informaatiovirta kietoutuneissa kvanttijärjestelmissä". Proceedings of the Royal Society of London Series A 456, 1759 (2000). arXiv:quant-ph/​9906007.
https: / / doi.org/ 10.1098 / rspa.2000.0585
arXiv: kvant-ph / 9906007

[2] Michael A. Levin ja Xiao-Gang Wen. "String-net kondensaatio: fyysinen mekanismi topologisille vaiheille". Phys. Rev. B 71, 045110 (2005). arXiv:cond-mat/​0404617.
https: / / doi.org/ 10.1103 / PhysRevB.71.045110
arXiv: kunto-matto / 0404617

[3] T. Senthil, Ashvin Vishwanath, Leon Balents, Subir Sachdev ja Matthew PA Fisher. "Defined kvanttikriittiset pisteet". Science 303, 1490–1494 (2004). arXiv:cond-mat/​0311326.
https: / / doi.org/ 10.1126 / science.1091806
arXiv: kunto-matto / 0311326

[4] Beni Yoshida. "Eksoottinen topologinen järjestys fraktaalispinnesteissä". Phys. Rev. B 88, 125122 (2013). arXiv:1302.6248.
https: / / doi.org/ 10.1103 / PhysRevB.88.125122
arXiv: 1302.6248

[5] Kevin Hartnett. "Matriisin kertolasku tuumaa lähempänä myyttistä tavoitetta". Quanta Magazine (2021). url: https://​/​www.quantamagazine.org/​mathematicians-inch-closer-to-matrix-multiplication-goal-20210323/​.
https://​/​www.quantamagazine.org/​mathematicians-inch-closer-to-matrix-multiplication-goal-20210323/​

[6] Volker Strassen. "Gaussin eliminaatio ei ole optimaalinen". Numerische Mathematik 13, 354–356 (1969).
https: / / doi.org/ 10.1007 / BF02165411

[7] Kevin Slagle. "Kvanttimittariverkot: uudenlainen tensoriverkko". Quantum 7, 1113 (2023). arXiv:2210.12151.
https:/​/​doi.org/​10.22331/​q-2023-09-14-1113
arXiv: 2210.12151

[8] Román Orús. "Käytännön johdatus tensoriverkkoihin: Matriisituotetilat ja ennustetut kietoutuvat paritilat". Annals of Physics 349, 117–158 (2014). arXiv:1306.2164.
https: / / doi.org/ 10.1016 / j.aop.2014.06.013
arXiv: 1306.2164

[9] Michael P. Zaletel ja Frank Pollmann. "Isometriset tensoriverkoston tilat kahdessa ulottuvuudessa". Phys. Rev. Lett. 124, 037201 (2020). arXiv:1902.05100.
https: / / doi.org/ 10.1103 / PhysRevLett.124.037201
arXiv: 1902.05100

[10] Steven Weinberg. "Kvanttimekaniikan testaus". Annals of Physics 194, 336–386 (1989).
https:/​/​doi.org/​10.1016/​0003-4916(89)90276-5

[11] N. Gisin. "Weinbergin epälineaarinen kvanttimekaniikka ja supraluminaalinen viestintä". Physics Letters A 143, 1–2 (1990).
https:/​/​doi.org/​10.1016/​0375-9601(90)90786-N

[12] Joseph Polchinski. "Weinbergin epälineaarinen kvanttimekaniikka ja Einstein-Podolsky-rosenin paradoksi". Phys. Rev. Lett. 66, 397-400 (1991).
https: / / doi.org/ 10.1103 / PhysRevLett.66.397

[13] Kevin Slagle. "Kvanttimekaniikan testaus meluisilla kvanttitietokoneilla" (2021). arXiv:2108.02201.
arXiv: 2108.02201

[14] Brian Swingle. "Ajan ulkopuolella olevien korrelaattorien fysiikan purkaminen". Nature Physics 14, 988–990 (2018).
https:/​/​doi.org/​10.1038/​s41567-018-0295-5

[15] Ignacio García-Mata, Rodolfo A. Jalabert ja Diego A. Wisniacki. "Ajan ulkopuolella olevat korrelaattorit ja kvanttikaaos" (2022). arXiv:2209.07965.
arXiv: 2209.07965

[16] Rahul Nandkishore ja David A. Huse. "Monen kehon lokalisointi ja termalisointi kvanttitilastomekaniikassa". Annual Review of Condensed Matter Physics 6, 15–38 (2015). arXiv:1404.0686.
https: / / doi.org/ 10.1146 / annurev-conmatphys-031214-014726
arXiv: 1404.0686

[17] Dmitry A. Abanin, Ehud Altman, Immanuel Bloch ja Maksym Serbyn. "Kollokviumi: Monen kehon lokalisointi, lämpökäsittely ja sotkeutuminen". Reviews of Modern Physics 91, 021001 (2019). arXiv:1804.11065.
https: / / doi.org/ 10.1103 / RevModPhys.91.021001
arXiv: 1804.11065

[18] Bruno Nachtergaele ja Robert Sims. "Paljon melua jostain: Miksi Lieb-Robinsonin rajat ovat hyödyllisiä" (2011). arXiv:1102.0835.
arXiv: 1102.0835

[19] Daniel A. Roberts ja Brian Swingle. "Lieb-robinson-sidottu ja perhonenefekti kvanttikenttäteorioissa". Phys. Rev. Lett. 117, 091602 (2016). arXiv:1603.09298.
https: / / doi.org/ 10.1103 / PhysRevLett.117.091602
arXiv: 1603.09298

[20] Zhiyuan Wang ja Kaden RA Hazzard. "Lieb-robinson-sidoksen kiristäminen paikallisesti vuorovaikutuksessa olevissa järjestelmissä". PRX Quantum 1, 010303 (2020). arXiv:1908.03997.
https: / / doi.org/ 10.1103 / PRXQuantum.1.010303
arXiv: 1908.03997

Viitattu

[1] Sayak Guha Roy ja Kevin Slagle, "Interpolointi kvanttidynamiikan mittarin ja Schrödingerin kuvien välillä", SciPost Physics Core 6 4, 081 (2023).

[2] Kevin Slagle, "Quantum Gauge Networks: A New Kind of Tensor Network", Kvantti 7, 1113 (2023).

Yllä olevat sitaatit ovat peräisin SAO: n ja NASA: n mainokset (viimeksi päivitetty onnistuneesti 2024-03-22 22:55:39). Lista voi olla puutteellinen, koska kaikki julkaisijat eivät tarjoa sopivia ja täydellisiä viittaustietoja.

On Crossrefin siteerattu palvelu tietoja teosten viittaamisesta ei löytynyt (viimeinen yritys 2024-03-22 22:55:38).

Tämä kirja on julkaistu Quantum - lehdessä Creative Commons Nimeäminen 4.0 Kansainvälinen (CC BY 4.0) lisenssin. Tekijänoikeudet säilyvät alkuperäisillä tekijänoikeuksien haltijoilla, kuten tekijöillä tai heidän instituutioillaan.

Aikaleima:

Lisää aiheesta Quantum Journal