Notation Big O et analyse d'algorithmes avec des exemples Python

Introduction

Il existe généralement plusieurs façons de résoudre le problème à l'aide d'un programme informatique. Par exemple, il existe plusieurs façons de trier les éléments dans un tableau - vous pouvez utiliser tri par fusion, tri à bulles, tri par insertion, et ainsi de suite. Tous ces algorithmes ont leurs propres avantages et inconvénients et le travail du développeur consiste à les peser pour pouvoir choisir le meilleur algorithme à utiliser dans n'importe quel cas d'utilisation. En d'autres termes, la question principale est de savoir quel algorithme utiliser pour résoudre un problème spécifique lorsqu'il existe plusieurs solutions au problème.

Analyse d'algorithme fait référence à l'analyse de la complexité de différents algorithmes et à la recherche de l'algorithme le plus efficace pour résoudre le problème posé. Notation Big-O est une mesure statistique utilisée pour décrire la complexité de l'algorithme.

Dans ce guide, nous allons d'abord passer brièvement en revue l'analyse des algorithmes, puis examiner de plus près la notation Big-O. Nous verrons comment la notation Big-O peut être utilisée pour trouver la complexité de l'algorithme à l'aide de différentes fonctions Python.

Pourquoi l'analyse d'algorithmes est-elle importante ?

Pour comprendre pourquoi l'analyse d'algorithmes est importante, nous prendrons l'aide d'un exemple simple. Supposons qu'un responsable confie à deux de ses employés la tâche de concevoir un algorithme en Python qui calcule la factorielle d'un nombre saisi par l'utilisateur. L'algorithme développé par le premier employé ressemble à ceci :

def fact(n):
    product = 1
    for i in range(n):
        product = product * (i+1)
    return product

print(fact(5))

Notez que l'algorithme prend simplement un entier comme argument. À l'intérieur de fact() fonction une variable nommée product est initialisé à 1. Une boucle s'exécute à partir de 1 à n et à chaque itération, la valeur dans le product est multiplié par le nombre itéré par la boucle et le résultat est stocké dans le product variable à nouveau. Après l'exécution de la boucle, le product variable contiendra la factorielle.

De même, le deuxième employé a également développé un algorithme qui calcule la factorielle d'un nombre. Le deuxième employé a utilisé une fonction récursive pour calculer la factorielle du nombre n:

def fact2(n):
    if n == 0:
        return 1
    else:
        return n * fact2(n-1)

print(fact2(5))

Le gestionnaire doit décider quel algorithme utiliser. Pour ce faire, ils ont décidé de choisir l'algorithme qui s'exécute le plus rapidement. Une façon de le faire est de trouver le temps nécessaire pour exécuter le code sur la même entrée.

Dans le notebook Jupyter, vous pouvez utiliser le %timeit littéral suivi de l'appel de la fonction pour trouver le temps d'exécution de la fonction :

%timeit fact(50)

Cela nous donnera :

9 µs ± 405 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

La sortie indique que l'algorithme prend microsecondes 9 (plus/moins 45 nanosecondes) par boucle.

De même, nous pouvons calculer combien de temps la deuxième approche prend pour s'exécuter :

%timeit fact2(50)

Cela se traduira par:

15.7 µs ± 427 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Le deuxième algorithme impliquant la récursivité prend microsecondes 15 (plus/moins 427 nanosecondes).

Le temps d'exécution montre que le premier algorithme est plus rapide par rapport au second algorithme impliquant la récursivité. Lorsqu'il s'agit d'entrées volumineuses, la différence de performances peut devenir plus importante.

Cependant, le temps d'exécution n'est pas une bonne mesure pour mesurer la complexité d'un algorithme car il dépend du matériel. Une métrique d'analyse de complexité plus objective pour un algorithme est nécessaire. C'est là que le Notation grand O vient de jouer.

Analyse d'algorithmes avec la notation Big-O

La notation Big-O signifie la relation entre l'entrée de l'algorithme et les étapes nécessaires pour exécuter l'algorithme. Il est indiqué par un grand "O" suivi d'une parenthèse ouvrante et fermante. À l'intérieur de la parenthèse, la relation entre l'entrée et les étapes franchies par l'algorithme est présentée à l'aide de "n".

La clé à retenir est que Big-O n'est pas intéressé par un particulier instance dans laquelle vous exécutez un algorithme, tel que fact(50), mais plutôt, dans quelle mesure escaliers compte tenu de l'apport croissant. C'est une bien meilleure métrique pour évaluer que le temps concret pour une instance concrète !

Par exemple, s'il y a un relation linéaire entre l'entrée et le pas pris par l'algorithme pour terminer son exécution, la notation Big-O utilisée sera O (n). De même, la notation Big-O pour fonctions quadratiques is O(n²).

Pour développer l'intuition :

• O (n): à n=1, 1 pas est franchi. À n=10, 10 étapes sont franchies.
• O(n²): à n=1, 1 pas est franchi. À n=10, 100 étapes sont franchies.

At n=1, ces deux-là effectueraient la même chose ! C'est une autre raison pour laquelle il vaut mieux observer la relation entre l'entrée et le nombre d'étapes pour traiter cette entrée que de simplement évaluer des fonctions avec une entrée concrète.

Voici quelques-unes des fonctions Big-O les plus courantes :

Nom	Grand O
Constante	O (c)
luminaires Néon Del	O (n)
Quadratique	O(n²)
Cubic	O(n³)
Exponentiel	O(2ⁿ)
Logarithmique	O (log (n))
Log Linéaire	O(nlog(n))

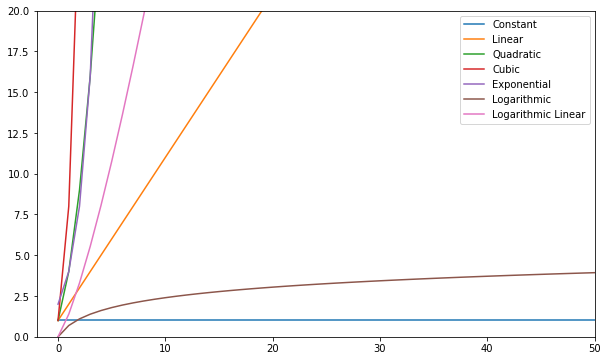
Vous pouvez visualiser ces fonctions et les comparer :

D'une manière générale, tout ce qui est pire que linéaire est considéré comme une mauvaise complexité (c'est-à-dire inefficace) et doit être évité si possible. La complexité linéaire est acceptable et généralement un mal nécessaire. Logarithmique c'est bien. Constant est incroyable !

Pour avoir une idée de la façon dont un Big-O est calculé, examinons quelques exemples de complexité constante, linéaire et quadratique.

Complexité constante – O(C)

La complexité d'un algorithme est dite constante si les étapes nécessaires pour terminer l'exécution d'un algorithme restent constantes, quel que soit le nombre d'entrées. La complexité constante est notée par O (c) De c peut être n'importe quel nombre constant.

Écrivons un algorithme simple en Python qui trouve le carré du premier élément de la liste, puis l'affiche à l'écran :

def constant_algo(items):
    result = items[0] * items[0]
    print(result)

constant_algo([4, 5, 6, 8])

Dans le script ci-dessus, quelle que soit la taille de l'entrée, ou le nombre d'éléments dans la liste d'entrée items, l'algorithme n'effectue que 2 étapes :

1. Trouver le carré du premier élément
2. Impression du résultat à l'écran.

La complexité reste donc constante.

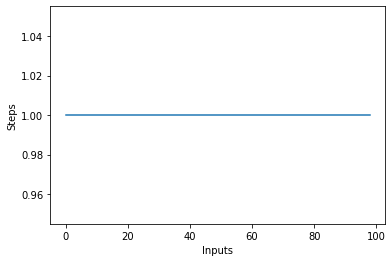
Si vous tracez un tracé linéaire avec la taille variable de la items entrée sur l'axe X et le nombre de pas sur l'axe Y, vous obtiendrez une ligne droite. Créons un court script pour nous aider à visualiser cela. Quel que soit le nombre d'entrées, le nombre d'étapes exécutées reste le même :

steps = []
def constant(n):
    return 1
    
for i in range(1, 100):
    steps.append(constant(i))
plt.plot(steps)

Complexité linéaire – O (n)

La complexité d'un algorithme est dite linéaire si les étapes nécessaires pour terminer l'exécution d'un algorithme augmentent ou diminuent linéairement avec le nombre d'entrées. La complexité linéaire est notée par O (n).

Dans cet exemple, écrivons un programme simple qui affiche tous les éléments de la liste sur la console :

def linear_algo(items):
    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

La complexité de la linear_algo() fonction est linéaire dans l'exemple ci-dessus puisque le nombre d'itérations de la boucle for sera égal à la taille de l'entrée items tableau. Par exemple, s'il y a 4 éléments dans le items list, la boucle for sera exécutée 4 fois.

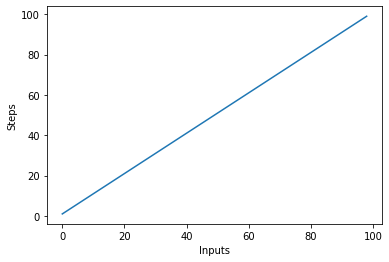
Créons rapidement un graphique pour l'algorithme de complexité linéaire avec le nombre d'entrées sur l'axe des x et le nombre d'étapes sur l'axe des y :

steps = []
def linear(n):
    return n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

Cela se traduira par:

Une chose importante à noter est qu'avec de grandes entrées, les constantes ont tendance à perdre de la valeur. C'est pourquoi nous supprimons généralement les constantes de la notation Big-O, et une expression telle que O(2n) est généralement raccourcie en O(n). O(2n) et O(n) sont tous deux linéaires – la relation linéaire est ce qui compte, pas la valeur concrète. Par exemple, modifions le linear_algo():

def linear_algo(items):
    for item in items:
        print(item)

    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Il y a deux boucles for qui itèrent sur l'entrée items liste. Par conséquent, la complexité de l'algorithme devient O (2n), cependant, dans le cas d'éléments infinis dans la liste d'entrée, le double de l'infini est toujours égal à l'infini. On peut ignorer la constante 2 (puisqu'il est finalement insignifiant) et la complexité de l'algorithme reste O (n).

Visualisons ce nouvel algorithme en traçant les entrées sur l'axe X et le nombre d'étapes sur l'axe Y :

steps = []
def linear(n):
    return 2*n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

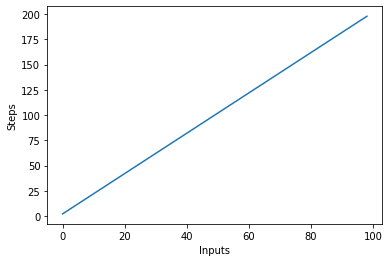
Dans le script ci-dessus, vous pouvez clairement voir que y=2n, cependant, la sortie est linéaire et ressemble à ceci :

Complexité quadratique – O(n²)

La complexité d'un algorithme est dite quadratique lorsque les étapes nécessaires à l'exécution d'un algorithme sont une fonction quadratique du nombre d'éléments en entrée. La complexité quadratique est notée O(n²):

def quadratic_algo(items):
    for item in items:
        for item2 in items:
            print(item, ' ' ,item2)

quadratic_algo([4, 5, 6, 8])

Nous avons une boucle externe qui parcourt tous les éléments de la liste d'entrée, puis une boucle interne imbriquée, qui parcourt à nouveau tous les éléments de la liste d'entrée. Le nombre total d'étapes effectuées est n*n, où n est le nombre d'éléments dans le tableau d'entrée.

Le graphique suivant trace le nombre d'entrées par rapport aux étapes d'un algorithme avec une complexité quadratique :

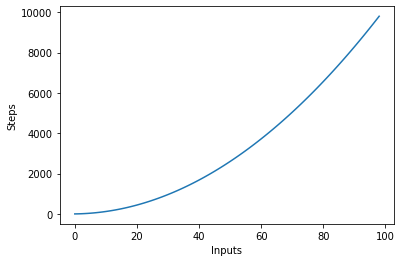
Complexité logarithmique – O (connexion)

Certains algorithmes atteignent une complexité logarithmique, comme Recherche binaire. La recherche binaire recherche un élément dans un tableau, en vérifiant la milieu d'un tableau, et élaguer la moitié dans laquelle l'élément n'est pas. Il recommence pour la moitié restante et continue les mêmes étapes jusqu'à ce que l'élément soit trouvé. A chaque étape, il moitiés le nombre d'éléments dans le tableau.

Cela nécessite que le tableau soit trié et que nous fassions une hypothèse sur les données (par exemple, qu'elles soient triées).

Lorsque vous pouvez faire des hypothèses sur les données entrantes, vous pouvez prendre des mesures qui réduisent la complexité d'un algorithme. La complexité logarithmique est souhaitable, car elle permet d'obtenir de bonnes performances même avec une entrée à grande échelle.

Trouver la complexité des fonctions complexes ?

Dans les exemples précédents, nous avions des fonctions assez simples en entrée. Cependant, comment calculons-nous le Big-O des fonctions qui appellent (plusieurs) autres fonctions sur l'entrée ?

Nous allons jeter un coup d'oeil:

def complex_algo(items):

    for i in range(5):
        print("Python is awesome")

    for item in items:
        print(item)

    for item in items:
        print(item)

    print("Big O")
    print("Big O")
    print("Big O")

complex_algo([4, 5, 6, 8])

Dans le script ci-dessus, plusieurs tâches sont en cours d'exécution, d'abord, une chaîne est imprimée 5 fois sur la console à l'aide de la print déclaration. Ensuite, nous imprimons la liste d'entrée deux fois sur l'écran, et enfin, une autre chaîne est imprimée trois fois sur la console. Pour trouver la complexité d'un tel algorithme, nous devons décomposer le code de l'algorithme en parties et essayer de trouver la complexité des pièces individuelles. Notez la complexité de chaque pièce.

Dans la première section, nous avons :

for i in range(5):
	print("Python is awesome")

La complexité de cette partie est O (5) puisque cinq étapes constantes sont exécutées dans ce morceau de code indépendamment de l'entrée.

Ensuite, nous avons :

for item in items:
	print(item)

Nous savons que la complexité du morceau de code ci-dessus est O (n). De même, la complexité du morceau de code suivant est également O (n):

for item in items:
	print(item)

Enfin, dans le morceau de code suivant, une chaîne est imprimée trois fois, d'où la complexité est O (3):

print("Big O")
print("Big O")
print("Big O")

Pour trouver la complexité globale, nous devons simplement ajouter ces complexités individuelles :

O(5) + O(n) + O(n) + O(3)

En simplifiant ce qui précède, nous obtenons :

O(8) + O(2n) = O(8+2n)

Nous avons dit précédemment que lorsque l'entrée (qui a une longueur n dans ce cas) devient extrêmement grande, les constantes deviennent insignifiantes, c'est-à-dire que deux fois ou la moitié de l'infini reste toujours l'infini. Par conséquent, nous pouvons ignorer les constantes. La complexité finale de l'algorithme sera O (n)!

Complexité des pires et des meilleurs cas

Habituellement, lorsque quelqu'un vous interroge sur la complexité d'un algorithme, il s'intéresse à la complexité du pire cas (Big-O). Parfois, ils peuvent également être intéressés par la complexité du meilleur cas (Big-Omega).

Pour comprendre la relation entre ceux-ci, examinons un autre morceau de code :

def search_algo(num, items):
    for item in items:
        if item == num:
            return True
        else:
            pass
nums = [2, 4, 6, 8, 10]

print(search_algo(2, nums))

Dans le script ci-dessus, nous avons une fonction qui prend un nombre et une liste de nombres en entrée. Elle renvoie vrai si le nombre passé est trouvé dans la liste des nombres, sinon elle renvoie None. Si vous recherchez 2 dans la liste, il sera trouvé dans la première comparaison. Il s'agit du meilleur cas de complexité de l'algorithme dans la mesure où l'élément recherché est trouvé dans le premier index recherché. La meilleure complexité de cas, dans ce cas, est O (1). En revanche, si vous recherchez 10, il sera trouvé au dernier index recherché. L'algorithme devra rechercher dans tous les éléments de la liste, d'où la complexité du pire des cas devient O (n).

En plus de la complexité du meilleur et du pire cas, vous pouvez également calculer la complexité moyenne (Big-Theta) d'un algorithme, qui vous dit "étant donné une entrée aléatoire, quelle est la complexité temporelle attendue de l'algorithme" ?

Complexité spatiale

En plus de la complexité temporelle, où vous comptez le nombre d'étapes nécessaires pour terminer l'exécution d'un algorithme, vous pouvez également trouver le complexité spatiale qui fait référence à la quantité d'espace que vous devez allouer en mémoire lors de l'exécution d'un programme.

Jetez un œil à l'exemple suivant :

def return_squares(n):
    square_list = []
    for num in n:
        square_list.append(num * num)

    return square_list

nums = [2, 4, 6, 8, 10]
print(return_squares(nums))

La return_squares() La fonction accepte une liste d'entiers et renvoie une liste avec les carrés correspondants. L'algorithme doit allouer de la mémoire pour le même nombre d'éléments que dans la liste d'entrée. Par conséquent, la complexité spatiale de l'algorithme devient O (n).

Conclusion

La notation Big-O est la métrique standard utilisée pour mesurer la complexité d'un algorithme. Dans ce guide, nous avons étudié ce qu'est la notation Big-O et comment elle peut être utilisée pour mesurer la complexité d'une variété d'algorithmes. Nous avons également étudié différents types de fonctions Big-O à l'aide de différents exemples Python. Enfin, nous avons brièvement passé en revue la complexité du pire et du meilleur cas ainsi que la complexité spatiale.