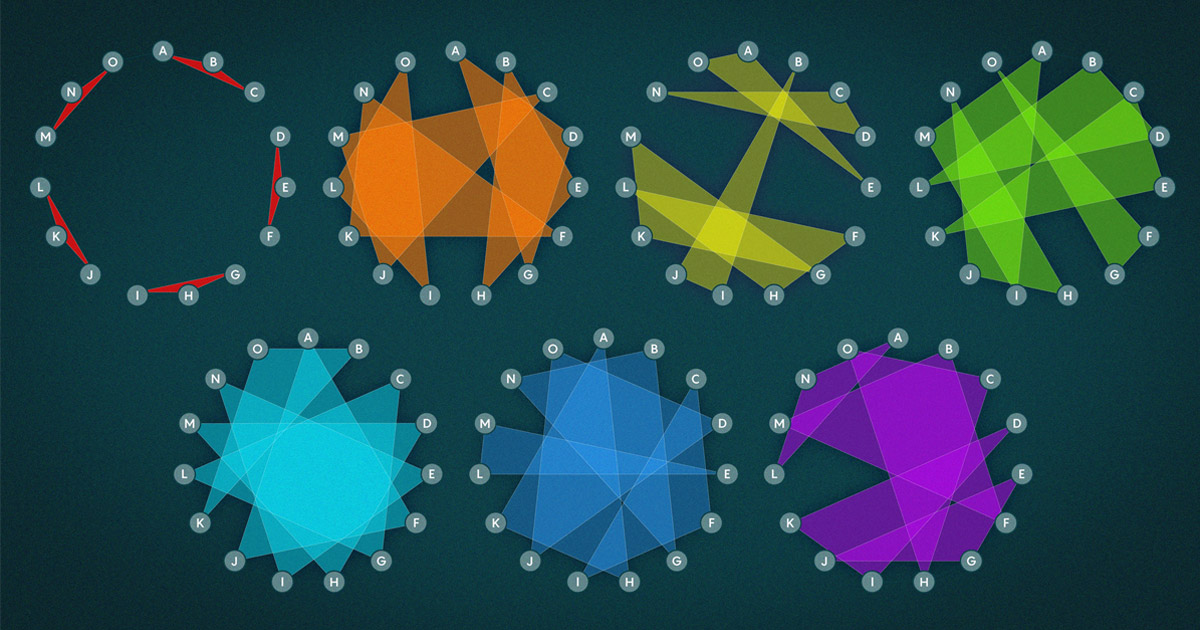
En 1850, Thomas Penyngton Kirkman, mathématicien, alors qu'il n'assumait pas sa principale responsabilité de vicaire dans l'Église d'Angleterre, décrivait son « problème d'écolière » : « Quinze jeunes filles d'une école sortent trois de front pendant sept jours de suite : il faut s'arranger pour chaque jour, afin que personne ne marche deux fois de front.
Pour un mathématicien moderne, ce type de problème est mieux imaginé comme un hypergraphe – un ensemble de nœuds rassemblés en groupes de trois ou plus. Les 15 écolières sont des nœuds, et chaque groupe de « trois de front » peut être considéré comme un triangle, avec trois lignes, ou bords, reliant trois nœuds.
Le problème de Kirkman demande essentiellement s'il existe un arrangement de ces triangles qui relie toutes les écolières les unes aux autres, mais avec la restriction supplémentaire qu'aucun triangle ne partage un bord. Le partage des avantages impliquerait que deux écolières doivent marcher ensemble plus d'une fois. Cette restriction signifie que chaque fille se promène avec deux nouveaux amis chaque jour pendant une semaine, de sorte que chaque couple possible se réunisse exactement une fois.
Ce problème et d’autres similaires ont séduit les mathématiciens pendant près de deux siècles depuis que Kirkman a posé sa question. En 1973, le légendaire mathématicien Paul Erdős en a posé une similaire. Il a demandé s'il était possible de construire un hypergraphe avec deux propriétés apparemment incompatibles. Premièrement, chaque paire de nœuds doit être reliée par exactement un triangle, comme pour les écolières. Cette propriété rend le graphique dense en triangles. La deuxième exigence impose un étalement très précis des triangles. (Plus précisément, cela nécessite que pour tout petit groupe de triangles, il y ait au moins trois nœuds de plus que de triangles.) "Vous avez ce comportement légèrement contradictoire où vous avez un objet global dense qui n'a pas de parties denses", a déclaré David Conlon, mathématicien au California Institute of Technology.
Ce mois de janvier, en une preuve complexe de 50 pages, quatre mathématiciens ont prouvé qu'il est toujours possible de construire un tel hypergraphe à condition de disposer de suffisamment de nœuds. « La quantité de détails techniques qu'ils ont dû accomplir, juste pour obtenir ça, c'était incroyable », a déclaré Allan Lo, mathématicien à l'Université de Birmingham. Conlon est d'accord : "C'est un travail vraiment impressionnant."
L'équipe de recherche a construit un système qui répondait aux exigences diaboliques d'Erdős en commençant par un processus aléatoire de choix des triangles et en le concevant avec un soin extrême pour répondre à leurs besoins. "Le nombre de modifications difficiles qui entrent dans la preuve est en fait assez stupéfiant", a déclaré Conlon.
Leur stratégie consistait à construire soigneusement l’hypergraphe à partir de triangles individuels. Par exemple, imaginez nos 15 écolières. Tracez une ligne entre chaque paire.
Le but ici est de tracer des triangles au-dessus de ces lignes de telle sorte que les triangles satisfassent à deux exigences : Premièrement, deux triangles ne partagent pas une arête. (Les systèmes qui remplissent cette exigence sont appelés systèmes triples de Steiner.) Et deuxièmement, assurez-vous que chaque petit sous-ensemble de triangles utilise un nombre suffisamment grand de nœuds.
La manière dont les chercheurs ont procédé est peut-être mieux comprise par une analogie.
Supposons qu'au lieu de créer des triangles avec des bords, vous construisez des maisons avec des briques Lego. Les premiers bâtiments que vous construisez sont extravagants, avec des renforts structurels et une ornementation élaborée. Une fois que vous avez terminé, mettez-les de côté. Ils serviront d'« absorbeur », une sorte de stock structuré.
Commencez maintenant à construire des bâtiments avec vos briques restantes, sans trop de planification. Lorsque votre réserve de Legos diminue, vous risquez de vous retrouver avec des briques égarées ou des maisons dont la structure est insalubre. Mais comme les bâtiments absorbants sont tellement surfaits et renforcés, vous pouvez arracher quelques briques ici et là et les utiliser sans risquer la catastrophe.
Dans le cas du triple système Steiner, vous essayez de créer des triangles. Votre absorbeur, dans ce cas, est un ensemble de bords soigneusement choisis. Si vous ne parvenez pas à trier le reste du système en triangles, vous pouvez utiliser certains des bords qui mènent à l'absorbeur. Ensuite, lorsque vous avez terminé, vous décomposez l'absorbeur lui-même en triangles.
L'absorption ne fonctionne pas toujours. Mais les mathématiciens ont bricolé le processus, trouvant de nouvelles façons de contourner les obstacles. Par exemple, une variante puissante appelée absorption itérative divise les arêtes en une séquence d’ensembles imbriqués, de sorte que chacun agisse comme un absorbeur pour le plus grand suivant.
« Au cours de la dernière décennie, des améliorations considérables ont été enregistrées », a déclaré Conlon. "C'est en quelque sorte une forme d'art, mais ils l'ont vraiment porté au niveau du grand art à ce stade."
Le problème d'Erdős était délicat même avec une absorption itérative. "Il est devenu assez rapidement clair pourquoi ce problème n'avait pas été résolu", a déclaré Mehtaab Sawhney, l'un des quatre chercheurs qui l'ont résolu, avec Ashvin Sah, qui, avec Sawhney, est étudiant diplômé au Massachusetts Institute of Technology ; Michael Simkin, chercheur postdoctoral au Centre des sciences et applications mathématiques de l'Université Harvard ; et Matthieu Kwan, mathématicien à l'Institut des sciences et technologies d'Autriche. "Il y avait des tâches techniques assez intéressantes, mais assez difficiles."
Par exemple, dans d'autres applications d'absorption itérative, une fois que vous avez fini de couvrir un ensemble — soit avec des triangles, pour les systèmes triples de Steiner, soit avec d'autres structures pour d'autres problèmes — vous pouvez le considérer comme réglé et l'oublier. Les conditions d'Erdős ont cependant empêché les quatre mathématiciens de le faire. Un groupe problématique de triangles pourrait facilement impliquer des nœuds provenant de plusieurs ensembles d’absorbeurs.
"Un triangle que vous avez choisi il y a 500 étapes, vous devez d'une manière ou d'une autre vous rappeler comment y penser", a déclaré Sawhney.
Ce que les quatre ont finalement compris, c'est que s'ils choisissaient leurs triangles avec soin, ils pourraient éviter d'avoir à garder une trace de chaque petite chose. "Ce qu'il est préférable de faire, c'est de penser à n'importe quel petit ensemble de 100 triangles et de garantir que cet ensemble de triangles est choisi avec la bonne probabilité", a déclaré Sawhney.
Les auteurs du nouvel article sont optimistes quant à la possibilité d’étendre leur technique au-delà de ce seul problème. Ils ont déjà appliqué leur stratégie à un problème concernant Carrés latins, qui sont comme une simplification d'un puzzle sudoku.
Au-delà de cela, plusieurs questions pourraient éventuellement céder le pas aux méthodes d’absorption, a déclaré Kwan. "Il y a tellement de problèmes en combinatoire, en particulier en théorie de la conception, où les processus aléatoires sont un outil très puissant." L’un de ces problèmes, la conjecture de Ryser-Brualdi-Stein, concerne également les carrés latins et attend une solution depuis les années 1960.
Même si l'absorption nécessite peut-être davantage de développement avant de pouvoir résoudre ce problème, elle a parcouru un long chemin depuis sa création il y a 30 ans, a déclaré Maya Stein, directeur adjoint du Centre de modélisation mathématique de l'Université du Chili. "C'est quelque chose de vraiment formidable à voir, comment ces méthodes évoluent."