Précision améliorée pour les simulations de trotteurs utilisant l'interpolation de Chebyshev

Précision améliorée pour les simulations de trotteurs utilisant l'interpolation de Chebyshev

Horodatage: 26 février 2024 9:34

Gumaro Rendon1, Jacob Watkins2et Nathan Wiebe3,4

1Zapata Computing Inc., Boston, MA 02110, États-Unis
2Installation de faisceaux d'isotopes rares, Michigan State University, East Lansing, MI 48824, États-Unis
3Département d'informatique, Université de Toronto, Toronto, ON M5S 2E4, Canada
4Pacific Northwest National Laboratory, Richland, WA 99352, États-Unis

Vous trouvez cet article intéressant ou souhaitez en discuter? Scite ou laisse un commentaire sur SciRate.

Abstract

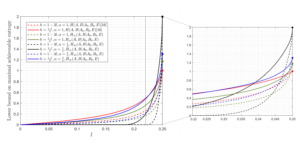
La métrologie quantique permet de mesurer les propriétés d'un système quantique à la limite optimale de Heisenberg. Cependant, lorsque les états quantiques pertinents sont préparés à l’aide d’une simulation hamiltonienne numérique, les erreurs algorithmiques accumulées entraîneront des écarts par rapport à cette limite fondamentale. Dans ce travail, nous montrons comment les erreurs algorithmiques dues à l’évolution temporelle trotterisée peuvent être atténuées grâce à l’utilisation de techniques d’interpolation polynomiale standard. Notre approche consiste à extrapoler jusqu'à une taille de pas Trotter nulle, semblable aux techniques d'extrapolation sans bruit pour atténuer les erreurs matérielles. Nous effectuons une analyse rigoureuse des erreurs de l'approche d'interpolation pour estimer les valeurs propres et les valeurs attendues évoluées dans le temps, et montrons que la limite de Heisenberg est atteinte jusqu'aux facteurs polylogarithmiques de l'erreur. Nos travaux suggèrent que des précisions proches de celles des algorithmes de simulation de pointe peuvent être obtenues en utilisant uniquement Trotter et les ressources classiques pour un certain nombre de tâches algorithmiques pertinentes.

Précision améliorée pour les simulations de trotter à l'aide de l'interpolation Chebyshev PlatoBlockchain Data Intelligence. Recherche verticale. Aï.

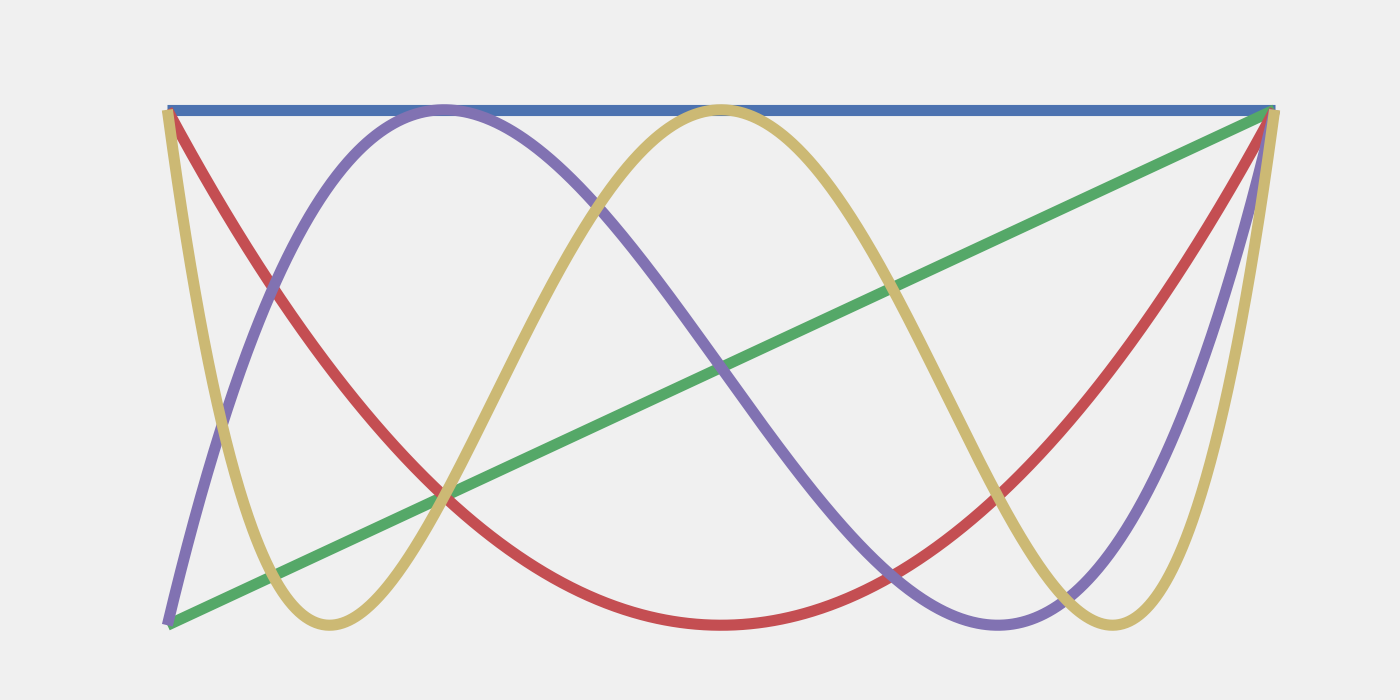
Image en vedette : Les cinq premiers polynômes de Chebyshev. L'interpolation aux zéros de Chebyshev constitue un schéma robuste pour l'atténuation des erreurs de Trotter.

[Contenu intégré]

Résumé populaire

Les ordinateurs quantiques ont le potentiel d’améliorer notre compréhension de la chimie, des matériaux, de la physique nucléaire et d’autres disciplines scientifiques grâce à une simulation quantique améliorée. Il existe plusieurs algorithmes quantiques disponibles pour cette tâche, parmi lesquels les formules de Trotter sont souvent préférées en raison de leur simplicité et de leurs faibles coûts initiaux. Malheureusement, les formules Trotter sont, en théorie, relativement imprécises par rapport à celles de leurs concurrents plus récents et plus sophistiqués. Bien qu’un temps de calcul plus long puisse s’avérer utile, cette stratégie devient rapidement ingérable sur les appareils quantiques bruyants d’aujourd’hui, avec une capacité limitée à effectuer des calculs longs et ininterrompus.

Pour atténuer les erreurs dans les simulations Trotter sans augmenter le temps de traitement quantique, nous utilisons des polynômes pour apprendre la relation entre l'erreur et la taille du pas. En collectant des données pour différents choix de taille de pas, nous pouvons interpoler, c'est-à-dire enfiler, les données avec un polynôme, puis estimer le comportement attendu pour de très petites tailles de pas. Nous prouvons mathématiquement que notre approche produit des améliorations de précision asymptotique par rapport au Trotter standard pour deux tâches fondamentales : l'estimation des valeurs propres et l'estimation des valeurs attendues.

Notre méthode est simple et pratique, ne nécessitant que des techniques standards en calcul quantique et classique. Nous pensons que nos travaux fournissent une base théorique solide pour des recherches plus approfondies sur l'atténuation des erreurs algorithmiques. Des extensions de ces travaux pourraient se produire dans plusieurs directions, depuis l’élimination des hypothèses artificielles dans notre analyse jusqu’à la démonstration de simulations quantiques améliorées.

► Données BibTeX

► Références

S. Lloyd, Simulateurs quantiques universels, Science 273 (1996) 1073.
https: / / doi.org/ 10.1126 / science.273.5278.1073

M. Reiher, N. Wiebe, KM Svore, D. Wecker et M. Troyer, Élucider les mécanismes de réaction sur les ordinateurs quantiques, Actes de l'Académie nationale des sciences 114 (2017) 7555.
https: / / doi.org/ 10.1073 / pnas.161915211

JD Whitfield, J. Biamonte et A. Aspuru-Guzik, Simulation de la structure électronique des Hamiltoniens à l'aide d'ordinateurs quantiques, Molecular Physics 109 (2011) 735.
https: / / doi.org/ 10.1080 / 00268976.2011.552441

J. Lee, DW Berry, C. Gidney, WJ Huggins, JR McClean, N. Wiebe et al., Des calculs quantiques de chimie encore plus efficaces grâce à l'hypercontraction tensorielle, PRX Quantum 2 (2021) 030305.
https: / / doi.org/ 10.1103 / PRXQuantum.2.030305

V. von Burg, GH Low, T. Häner, DS Steiger, M. Reiher, M. Roetteler et al., Catalyse informatique améliorée par l'informatique quantique, Physical Review Research 3 (2021) 033055.
https: / / doi.org/ 10.1103 / PhysRevResearch.3.033055

SP Jordan, KS Lee et J. Preskill, Algorithmes quantiques pour les théories quantiques des champs, Science 336 (2012) 1130.
https: / / doi.org/ 10.1126 / science.1217069

AF Shaw, P. Lougovski, JR Stryker et N. Wiebe, Algorithmes quantiques pour simuler le modèle de Schwinger sur réseau, Quantum 4 (2020) 306.
https:/​/​doi.org/​10.22331/​q-2020-08-10-306

N. Klco, MJ Savage et JR Stryker, Su (2) théorie des champs de jauge non abéliens en une dimension sur les ordinateurs quantiques numériques, Physical Review D 101 (2020) 074512.
https: / / doi.org/ 10.1103 / PhysRevD.101.074512

AM Childs et N. Wiebe, Simulation hamiltonienne utilisant des combinaisons linéaires d'opérations unitaires, Quantum Info. Calculer. 12 (2012) 901-924.
https: / / doi.org/ 10.26421 / QIC12.11-12-1

GH Low, V. Kliuchnikov et N. Wiebe, Simulation hamiltonienne multiproduit bien conditionnée, arXiv : 1907.11679 (2019).
https://​/​doi.org/​10.48550/​arXiv.1907.11679
arXiv: 1907.11679

DW Berry, AM Childs, R. Cleve, R. Kothari et RD Somma, Simulation de la dynamique hamiltonienne avec une série taylor tronquée, Lettres d'examen physique 114 (2015) 090502.
https: / / doi.org/ 10.1103 / PhysRevLett.114.090502

GH Low et N. Wiebe, simulation hamiltonienne dans l'image d'interaction, arXiv : 1805.00675 (2018).
https://​/​doi.org/​10.48550/​arXiv.1805.00675
arXiv: 1805.00675

M. Kieferová, A. Scherer et DW Berry, Simulation de la dynamique des hamiltoniens dépendants du temps avec une série de dysons tronquées, Physical Review A 99 (2019) 042314.
https: / / doi.org/ 10.1103 / PhysRevA.99.042314

GH Low et IL Chuang, Simulation hamiltonienne par qubitisation, Quantum 3 (2019) 163.
https:/​/​doi.org/​10.22331/​q-2019-07-12-163

R. Babbush, C. Gidney, DW Berry, N. Wiebe, J. McClean, A. Paler et al., Codage des spectres électroniques dans des circuits quantiques avec une complexité t linéaire, Physical Review X 8 (2018) 041015.
https: / / doi.org/ 10.1103 / PhysRevX.8.041015

DW Berry, G. Ahokas, R. Cleve et BC Sanders, Algorithmes quantiques efficaces pour simuler des hamiltoniens clairsemés, Communications in Mathematical Physics 270 (2006) 359-371.
https: / / doi.org/ 10.1007 / s00220-006-0150-x

N. Wiebe, DW Berry, P. Høyer et BC Sanders, Simulation de la dynamique quantique sur un ordinateur quantique, Journal of Physics A : Mathematical and Theoretical 44 (2011) 445308.
https:/​/​doi.org/​10.1088/​1751-8113/​44/​44/​445308

AM Childs, Y. Su, MC Tran, N. Wiebe et S. Zhu, Théorie de l'erreur de trotteur avec mise à l'échelle du collecteur, Physical Review X 11 (2021) 011020.
https: / / doi.org/ 10.1103 / PhysRevX.11.011020

J. Haah, MB Hastings, R. Kothari et GH Low, Algorithme quantique pour simuler l'évolution en temps réel des hamiltoniens sur réseau, SIAM Journal on Computing (2021) FOCS18.
https: / / doi.org/ 10.1137 / 18M12315

M. Hagan et N. Wiebe, Simulations quantiques composites, arXiv :2206.06409 (2022).
https:/​/​doi.org/​10.22331/​q-2023-11-14-1181
arXiv: 2206.06409

GH Low, Y. Su, Y. Tong et MC Tran, Sur la complexité de la mise en œuvre des étapes du trotteur, arXiv :2211.09133 (2022).
https: / / doi.org/ 10.1103 / PRXQuantum.4.020323
arXiv: 2211.09133

GH Low et IL Chuang, Simulation hamiltonienne optimale par traitement du signal quantique, Physical Review Letters 118 (2017).
https: / / doi.org/ 10.1103 / physrevlett.118.010501

S. Endo, Q. Zhao, Y. Li, S. Benjamin et X. Yuan, Atténuation des erreurs algorithmiques dans une simulation hamiltonienne, Phys. Rév.A 99 (2019) 012334.
https: / / doi.org/ 10.1103 / PhysRevA.99.012334

AC Vazquez, R. Hiptmair et S. Woerner, Amélioration de l'algorithme des systèmes linéaires quantiques à l'aide de l'extrapolation de Richardson, ACM Transactions on Quantum Computing 3 (2022).
https: / / doi.org/ 10.1145 / 3490631

AC Vazquez, DJ Egger, D. Ochsner et S. Woerner, Formules multiproduits bien conditionnées pour une simulation hamiltonienne respectueuse du matériel, Quantum 7 (2023) 1067.
https:/​/​doi.org/​10.22331/​q-2023-07-25-1067

M. Suzuki, Théorie générale des intégrales de chemin fractal avec applications aux théories à N corps et à la physique statistique, Journal of Mathematical Physics 32 (1991) 400.
https: / / doi.org/ 10.1063 / 1.529425

A. Gilyén, Y. Su, GH Low et N. Wiebe, Transformation des valeurs singulières quantiques et au-delà : améliorations exponentielles pour l'arithmétique matricielle quantique, dans Actes du 51e symposium annuel ACM SIGACT sur la théorie de l'informatique, pp. 193-204, 2019 , EST CE QUE JE.
https: / / doi.org/ 10.1145 / 3313276.3316366

C. Yi et E. Crosson, Analyse spectrale des formules de produits pour la simulation quantique, npj Quantum Information 8 (2022) 37.
https: / / doi.org/ 10.1038 / s41534-022-00548-w

A. Quarteroni, R. Sacco et F. Saleri, Mathématiques numériques, vol. 37, Springer Science & Business Media (2010), 10.1007/​b98885.
https: / / doi.org/ 10.1007 / b98885

F. Piazzon et M. Vianello, Inégalités de stabilité pour les constantes de Lebesgue via des inégalités de type Markov, Notes de recherche sur les Dolomites sur l'approximation 11 (2018).

AP de Camargo, Sur la stabilité numérique de la formule de Newton pour l'interpolation de Lagrange, Journal of Computational and Applied Mathematics 365 (2020) 112369.
https://​/​doi.org/​10.1016/​j.cam.2019.112369

L. Trefethen, Six mythes de l'interpolation polynomiale et de la quadrature, (2011).

W. Gautschi, Dans quelle mesure les systèmes de Vandermonde sont-ils (in)stables ? analyse asymptotique et informatique, dans Notes de cours en mathématiques pures et appliquées, pp. 193-210, Marcel Dekker, Inc, 1990.

NJ Higham, La stabilité numérique de l'interpolation barycentrique de Lagrange, IMA Journal of Numerical Analysis 24 (2004) 547.
https://​/​doi.org/​10.1093/​imanum/​24.4.547

JC Mason et DC Handscomb, Polynômes de Chebyshev, CRC press (2002), 10.1201/​9781420036114.
https: / / doi.org/ 10.1201 / 9781420036114

G. Rendon, T. Izubuchi et Y. Kikuchi, Effets de la fenêtre effilée du cosinus sur l'estimation de la phase quantique, Physical Review D 106 (2022) 034503.
https: / / doi.org/ 10.1103 / PhysRevD.106.034503

LN Trefethen, Théorie de l'approximation et pratique de l'approximation, édition étendue, SIAM (2019), 10.1137/​1.9781611975949.
https: / / doi.org/ 10.1137 / 1.9781611975949

FL Bauer et CT Fike, Normes et théorèmes d'exclusion, Numer. Mathématiques. 2 (1960) 137-141.
https: / / doi.org/ 10.1007 / BF01386217

S. Blanes, F. Casas, J.-A. Oteo et J. Ros, L'expansion magnus et certaines de ses applications, Physics reports 470 (2009) 151.
https: / / doi.org/ 10.1016 / j.physrep.2008.11.001

N. Klco et MJ Savage, Préparation d'états minimalement intriqués de fonctions d'onde localisées sur des ordinateurs quantiques, Physical Review A 102 (2020).
https: / / doi.org/ 10.1103 / physreva.102.012612

JJ García-Ripoll, Algorithmes d'inspiration quantique pour l'analyse multivariée : de l'interpolation aux équations aux dérivées partielles, Quantum 5 (2021) 431.
https:/​/​doi.org/​10.22331/​q-2021-04-15-431

W. Górecki, R. Demkowicz-Dobrzański, HM Wiseman et DW Berry, limite de Heisenberg corrigée en $pi$, lettres d'examen physique 124 (2020) 030501.
https: / / doi.org/ 10.1103 / PhysRevLett.124.030501

D. Grinko, J. Gacon, C. Zoufal et S. Woerner, Estimation itérative de l'amplitude quantique, npj Quantum Information 7 (2021) 52 [1912.05559].
https:/​/​doi.org/​10.1038/​s41534-021-00379-1
arXiv: 1912.05559

N. Wiebe, D. Berry, P. Høyer et BC Sanders, Décompositions d'ordre supérieur des exponentielles d'opérateurs ordonnés, Journal of Physics A : Mathematical and Theoretical 43 (2010) 065203.
https:/​/​doi.org/​10.1088/​1751-8113/​43/​6/​065203

RA Horn et CR Johnson, Analyse matricielle, Cambridge University Press (2012), 10.1017/​CBO9780511810817.
https: / / doi.org/ 10.1017 / CBO9780511810817

M. Chiani, D. Dardari et MK Simon, Nouvelles limites exponentielles et approximations pour le calcul de la probabilité d'erreur dans les canaux à évanouissement, IEEE Transactions on Wireless Communications 2 (2003) 840.
https://​/​doi.org/​10.1109/​TWC.2003.814350

JM Borwein et PB Borwein, Pi et l'AGM : une étude sur la théorie analytique des nombres et la complexité informatique, Wiley-Interscience (1987).

BL Higgins, DW Berry, SD Bartlett, HM Wiseman et GJ Pryde, Estimation de phase limitée par Heisenberg sans enchevêtrement, Nature 450 (2007) 393.
https: / / doi.org/ 10.1038 / nature06257

RB Griffiths et C.-S. Niu, Transformation de Fourier semi-classique pour le calcul quantique, Physical Review Letters 76 (1996) 3228.
https: / / doi.org/ 10.1103 / PhysRevLett.76.3228

AY Kitaev, Mesures quantiques et problème du stabilisateur abélien, quant-ph/​9511026 (1995).
https://​/​doi.org/​10.48550/​arXiv.quant-ph/​9511026
arXiv: quant-ph / 9511026

DS Abrams et S. Lloyd, Algorithme quantique fournissant une augmentation exponentielle de la vitesse pour trouver des valeurs propres et des vecteurs propres, Physical Review Letters 83 (1999) 5162.
https: / / doi.org/ 10.1103 / PhysRevLett.83.5162

J. Watkins, N. Wiebe, A. Roggero et D. Lee, Simulation hamiltonienne dépendante du temps utilisant des constructions d'horloges discrètes, arXiv :2203.11353 (2022).
https://​/​doi.org/​10.48550/​arXiv.2203.11353
arXiv: 2203.11353

TD Ahle, Limites nettes et simples pour les moments bruts des distributions binomiales et de poisson, Statistics & Probability Letters 182 (2022) 109306.
https://​/​doi.org/​10.1016/​j.spl.2021.109306

T. Rivlin, Polynômes de Chebyshev, Dover Books on Mathematics, Dover Publications (2020).

Cité par

[1] Dean Lee, « Techniques quantiques pour les problèmes de valeurs propres », Journal physique européen A 59 11, 275 (2023).

[2] Tatsuhiko N. Ikeda, Hideki Kono et Keisuke Fujii, « Trotter24 : Une trottérisation adaptative de taille garantie avec précision pour les simulations hamiltoniennes », arXiv: 2307.05406, (2023).

[3] Hans Hon Sang Chan, Richard Meister, Matthew L. Goh et Bálint Koczor, "Algorithmic Shadow Spectroscopy", arXiv: 2212.11036, (2022).

[4] Sergiy Zhuk, Niall Robertson et Sergey Bravyi, « Limites d'erreur de Trotter et formules multiproduits dynamiques pour la simulation hamiltonienne », arXiv: 2306.12569, (2023).

[5] Zhicheng Zhang, Qisheng Wang et Mingsheng Ying, "Algorithme quantique parallèle pour la simulation hamiltonienne", Quantique 8, 1228 (2024).

[6] Lea M. Trenkwalder, Eleanor Scerri, Thomas E. O'Brien et Vedran Dunjko, « Compilation de simulation hamiltonienne de formule produit via l'apprentissage par renforcement », arXiv: 2311.04285, (2023).

[7] Gumaro Rendon et Peter D. Johnson, « Estimation énergétique de l'état gaussien à faible profondeur », arXiv: 2309.16790, (2023).

[8] Gregory Boyd, « Low-Overhead Parallélisation de LCU via Commuting Operators », arXiv: 2312.00696, (2023).

Les citations ci-dessus proviennent de SAO / NASA ADS (dernière mise à jour réussie 2024-02-27 02:40:25). La liste peut être incomplète car tous les éditeurs ne fournissent pas de données de citation appropriées et complètes.

On Le service cité par Crossref aucune donnée sur la citation des œuvres n'a été trouvée (dernière tentative 2024-02-27 02:40:24).

Cet article est publié dans Quantum sous le Creative Commons Attribution 4.0 International (CC BY 4.0) Licence. Le droit d'auteur reste la propriété des détenteurs d'origine tels que les auteurs ou leurs institutions.

Horodatage:

Plus de Journal quantique