Les mathématiciens lancent des dés et obtiennent pierre-papier-ciseaux

Comme Bill Gates raconte l'histoire, Warren Buffett l'a un jour défié à un jeu de dés. Chacun sélectionnerait l'un des quatre dés appartenant à Buffett, puis ils lanceraient, le plus grand nombre gagnant. Ce n'étaient pas des dés standard - ils avaient un assortiment de nombres différent de celui habituel de 1 à 6. Buffett a proposé de laisser Gates choisir en premier, afin qu'il puisse choisir le dé le plus fort. Mais après que Gates ait examiné les dés, il a renvoyé une contre-proposition : Buffett devrait choisir en premier.

Gates avait reconnu que les dés de Buffett présentaient une curieuse propriété : aucun d'entre eux n'était le plus fort. Si Gates avait choisi en premier, alors quel que soit le dé qu'il avait choisi, Buffett aurait pu trouver un autre dé qui pourrait le battre (c'est-à-dire un dé avec plus de 50% de chances de gagner).

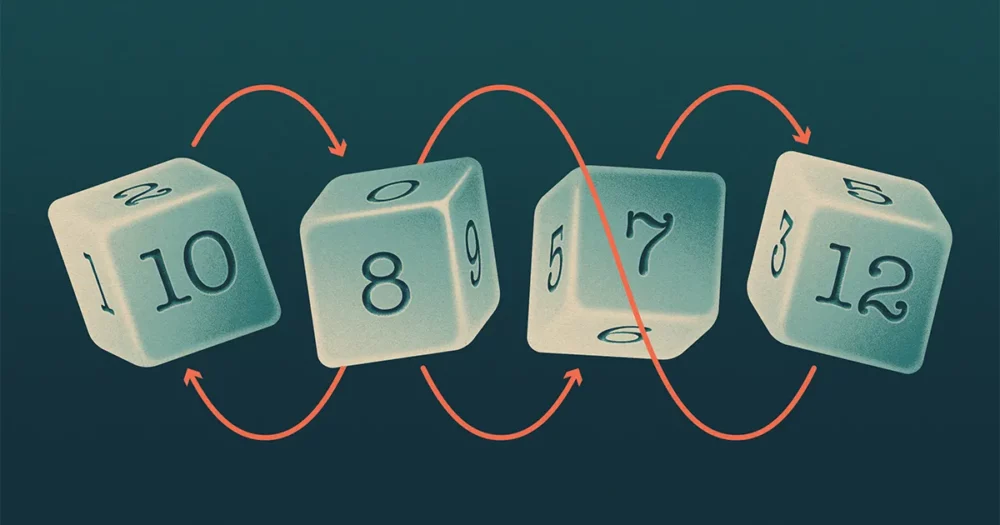
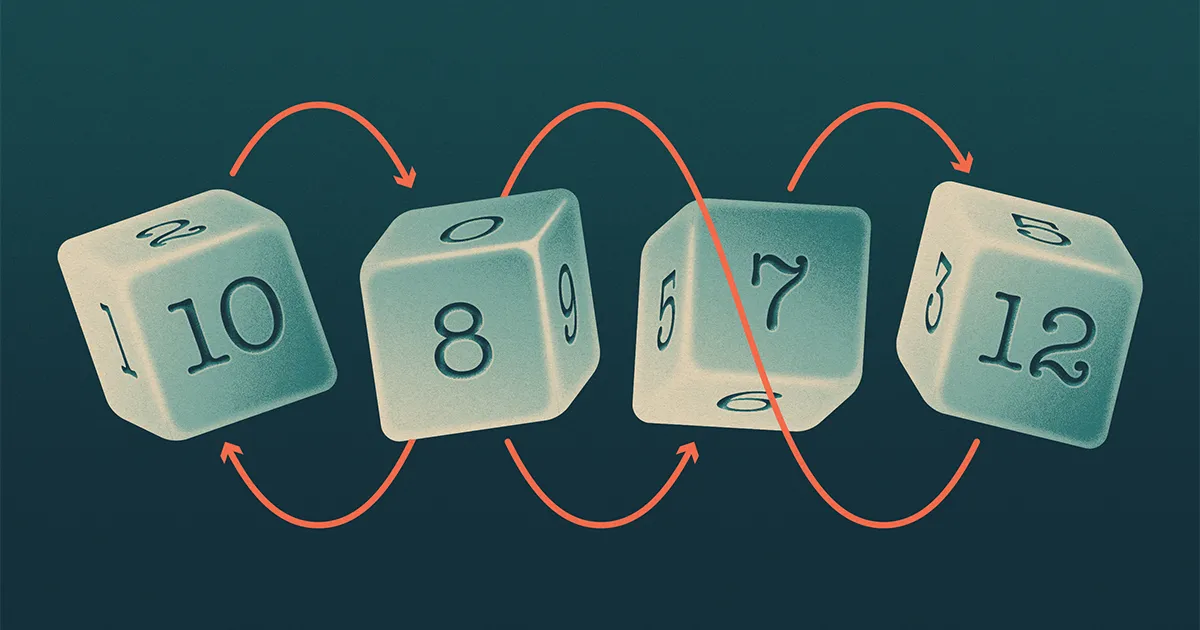
Les quatre dés de Buffett (appelez-les A, B, C ainsi que D) formaient un motif rappelant les ciseaux à pierre et papier, dans lesquels A battements B, B battements C, C battements D ainsi que D battements A. Les mathématiciens disent qu'un tel ensemble de dés est "intransitif".

"Ce n'est pas du tout intuitif que [les dés intransitifs] existent même", a déclaré Brian Conrey, le directeur de l'American Institute of Mathematics (AIM) à San Jose, qui a écrit un article influent sur le sujet en 2013.

Les mathématiciens ont trouvé premiers exemples de dés intransitifs il y a plus de 50 ans, et finalement prouvé que lorsque vous considérez des dés avec de plus en plus de côtés, il est possible de créer des cycles intransitifs de n'importe quelle longueur. Ce que les mathématiciens ne savaient pas jusqu'à récemment, c'est à quel point les dés intransitifs sont courants. Devez-vous concevoir de tels exemples avec soin, ou pouvez-vous choisir des dés au hasard et avoir une bonne chance de trouver un ensemble intransitif ?

En regardant trois dés, si vous savez que A battements B ainsi que B battements C, cela semble être la preuve que A est le plus fort; situations où C battements A devrait être rare. Et en effet, si les nombres sur les dés sont autorisés à s'additionner à des totaux différents, alors les mathématiciens croient que cette intuition est vraie.

Mais un article mis en ligne la fin de l'année dernière montre que dans un autre cadre naturel, cette intuition échoue de manière spectaculaire. Supposons que vous exigez que vos dés n'utilisent que les nombres qui apparaissent sur un dé normal et aient le même total qu'un dé normal. Ensuite, le papier a montré, si A battements B ainsi que B battements C, A ainsi que C ont essentiellement des chances égales de l'emporter l'une contre l'autre.

"Sachant que A battements B ainsi que B battements C ne vous donne simplement aucune information sur la question de savoir si A battements C," m'a dit Timothy Gowers de l'Université de Cambridge, médaillé Fields et l'un des contributeurs au nouveau résultat, qui a été prouvé via une collaboration en ligne ouverte connue sous le nom de projet Polymath.

Pendant ce temps, un autre étude récente analyse des ensembles de quatre dés ou plus. Cette constatation est sans doute encore plus paradoxale : si, par exemple, vous piochez quatre dés au hasard et que vous constatez que A battements B, B battements C ainsi que C battements D, alors c'est légèrement PLUS probablement pour D battre A que l'inverse.

Ni fort ni faible

La récente vague de résultats a commencé il y a environ une décennie, après que Conrey ait assisté à un rassemblement pour les professeurs de mathématiques avec une session qui couvrait les dés intransitifs. "Je n'avais aucune idée que de telles choses pouvaient exister", a-t-il déclaré. "Je suis devenu un peu fasciné par eux."

Il a décidé (rejoint plus tard par son collègue Kent Morrisson à AIM) pour explorer le sujet avec trois lycéens qu'il encadrait - James Gabbard, Katie Grant et Andrew Liu. À quelle fréquence, se demande le groupe, des dés choisis au hasard formeront-ils un cycle intransitif ?

On pense que les ensembles de dés intransitifs sont rares si les nombres de faces des dés s'additionnent à des totaux différents, car le dé avec le total le plus élevé est susceptible de battre les autres. L'équipe a donc décidé de se concentrer sur les dés qui ont deux propriétés : Premièrement, les dés utilisent les mêmes nombres que sur un dé standard - de 1 à n, dans le cas d'un ndé à face. Et deuxièmement, les nombres de visages totalisent le même total que sur un dé standard. Mais contrairement aux dés standard, chaque dé peut répéter certains nombres et en omettre d'autres.

Dans le cas des dés à six faces, il n'y a que 32 dés différents qui ont ces deux propriétés. Ainsi, à l'aide d'un ordinateur, l'équipe a pu identifier tous les triplets dans lesquels A battements B ainsi que B battements C. Les chercheurs ont constaté, à leur grand étonnement, que A battements C en 1,756 XNUMX triples et C battements A en 1,731 XNUMX triplets - des nombres presque identiques. Sur la base de ce calcul et de simulations de dés à plus de six faces, l'équipe a conjecturé que lorsque le nombre de faces du dé tend vers l'infini, la probabilité que A battements C approche les 50 %.

La conjecture, avec son mélange d'accessibilité et de nuance, a semblé à Conrey un bon fourrage pour un projet Polymath, dans lequel de nombreux mathématiciens se réunissent en ligne pour partager des idées. À la mi-2017, il a proposé l'idée à Gowers, à l'origine de l'approche Polymath. "J'ai beaucoup aimé la question, en raison de sa valeur de surprise", a déclaré Gowers. Il a écrit un blog récents à propos de la conjecture qui a suscité une vague de commentaires, et au cours de six messages supplémentaires, les commentateurs ont réussi à le prouver.

Dans leur document, posté en ligne fin novembre 2022, un élément clé de la preuve consiste à montrer que, pour la plupart, cela n'a pas de sens de dire si un seul dé est fort ou faible. Les dés de Buffett, dont aucun n'est le plus fort de la meute, ne sont pas si inhabituels : si vous choisissez un dé au hasard, le projet Polymath a montré qu'il est susceptible de battre environ la moitié des autres dés et de perdre contre l'autre moitié. "Presque chaque dé est assez moyen", a déclaré Gowers.

Le projet a divergé du modèle original de l'équipe AIM sur un point : pour simplifier certains aspects techniques, le projet a déclaré que l'ordre des nombres sur un dé était important ; ainsi, par exemple, 122556 et 152562 seraient considérés comme deux dés différents. Mais le résultat Polymath, combiné aux preuves expérimentales de l'équipe AIM, crée une forte présomption que la conjecture est également vraie dans le modèle original, a déclaré Gowers.

"J'étais absolument ravi qu'ils aient trouvé cette preuve", a déclaré Conrey.

En ce qui concerne les collections de quatre dés ou plus, l'équipe AIM avait prédit un comportement similaire à celui de trois dés : par exemple, si A battements B, B battements C ainsi que C battements D alors il devrait y avoir une probabilité d'environ 50-50 que D battements A, se rapprochant exactement de 50-50 lorsque le nombre de faces du dé tend vers l'infini.

Pour tester la conjecture, les chercheurs ont simulé des tournois en tête-à-tête pour des ensembles de quatre dés à 50, 100, 150 et 200 faces. Les simulations n'obéissaient pas aussi étroitement à leurs prédictions que dans le cas de trois dés, mais étaient encore suffisamment proches pour renforcer leur croyance en la conjecture. Mais bien que les chercheurs ne s'en soient pas rendu compte, ces petits écarts portaient un message différent : pour des ensembles de quatre dés ou plus, leur conjecture est fausse.

"Nous voulions vraiment que [la conjecture] soit vraie, parce que ce serait cool", a déclaré Conrey.

Dans le cas de quatre dés, Cornacchia Elisabetta de l'Ecole polytechnique fédérale de Lausanne et Jan Hazła de l'Institut Africain des Sciences Mathématiques à Kigali, Rwanda, a montré dans un papier mis en ligne fin 2020 que si A battements B, B battements C ainsi que C battements D, puis D a un peu plus de 50 % de chances de battre A – probablement quelque part autour de 52%, a déclaré Hązła. (Comme pour l'article Polymath, Cornacchia et Hązła ont utilisé un modèle légèrement différent de celui de l'article AIM.)

La découverte de Cornacchia et Hązła découle du fait que même si, en règle générale, un seul dé ne sera ni fort ni faible, une paire de dés peut parfois avoir des zones de force communes. Si vous choisissez deux dés au hasard, ont montré Cornacchia et Hązła, il y a une probabilité décente que les dés soient corrélés : ils auront tendance à battre ou à perdre contre les mêmes dés. "Si je vous demande de créer deux dés proches l'un de l'autre, il s'avère que c'est possible", a déclaré Hązła. Ces petites poches de corrélation éloignent les résultats des tournois de la symétrie dès qu'il y a au moins quatre dés dans l'image.

Les articles récents ne sont pas la fin de l'histoire. L'article de Cornacchia et Hązła ne fait que commencer à découvrir précisément comment les corrélations entre les dés déséquilibrent la symétrie des tournois. En attendant, cependant, nous savons maintenant qu'il existe de nombreux ensembles de dés intransitifs - peut-être même un assez subtil pour inciter Bill Gates à choisir en premier.