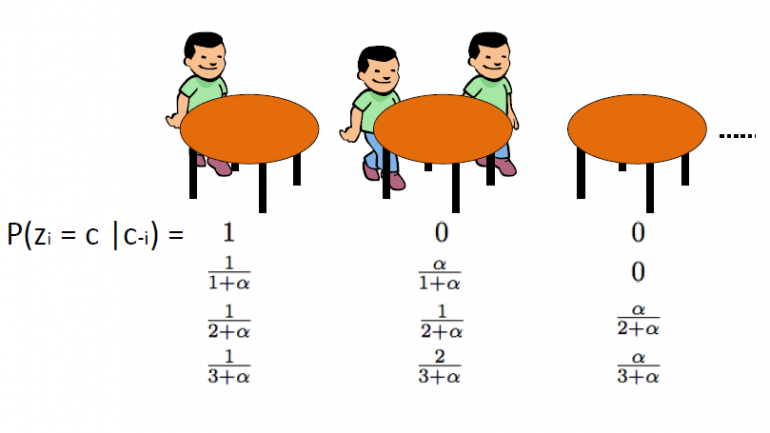Le processus Dirichlet le processus de restauration chinois et autres représentations

• 20 mai 2014
• Vassilis Vryniotis
• . Sans commentaires

Cet article est la troisième partie de la série sur le clustering avec les modèles de mélange de processus Dirichlet. La fois précédente, nous avons défini le modèle de mélange fini basé sur la distribution de Dirichlet et nous avons posé des questions sur la façon dont nous pouvons rendre ce modèle particulier infini. Nous avons brièvement discuté de l'idée de prendre la limite du modèle lorsque le nombre k de clusters tend vers l'infini mais comme nous l'avons souligné, l'existence d'un tel objet n'est pas anodine (en d'autres termes, comment pouvons-nous réellement «prendre la limite d'un modèle »?). Pour rappel, la raison pour laquelle nous voulons prendre make k infini est que nous aurons ainsi un modèle non paramétrique qui ne nous oblige pas à prédéfinir le nombre total de clusters dans les données.

Mise à jour: le Datumbox Machine Learning Framework est désormais open-source et gratuit pour download. Consultez le package com.datumbox.framework.machinelearning.clustering pour voir l'implémentation de Dirichlet Process Mixture Models en Java.

Même si notre objectif est de créer un modèle capable d'effectuer un clustering sur des ensembles de données, avant cela, nous devons discuter des processus Dirichlet. Nous fournirons à la fois les définitions mathématiques strictes et les explications plus intuitives de DP et nous discuterons des moyens de construire le processus. Ces constructions / représentations peuvent être vues comme un moyen de trouver des occurrences du processus de Dirichlet dans la «vraie vie».

Malgré le fait que j'ai essayé d'adapter mon rapport de recherche de manière à ce que ces articles de blog soient plus faciles à suivre, il est toujours important de définir les outils mathématiques et les distributions nécessaires avant de nous lancer dans l'utilisation des modèles. Les modèles de processus de Dirichlet sont un sujet de recherche active, mais ils nécessitent une bonne compréhension des statistiques et des processus stochastiques avant de les utiliser. Un autre problème est que, comme nous le verrons dans cet article, les processus Dirichlet peuvent être représentés / construits de nombreuses façons. En conséquence, plusieurs articles académiques utilisent des notations / conventions complètement différentes et examinent le problème de différents points de vue. Dans cet article, j'essaie de les expliquer aussi simplement que possible et d'utiliser la même notation. Espérons que les choses deviendront plus claires avec les deux articles à venir qui se concentrent sur la définition des modèles de mélange de processus Dirichlet et sur la façon de les utiliser réellement pour effectuer une analyse de cluster.

1. Définition du processus Dirichlet

Un processus de Dirichlet sur un espace Θ est un processus stochastique. C'est une distribution de probabilité sur des «distributions de probabilité sur un espace» et un en tirer est une distribution discrète. Plus formellement, une distribution de Dirichlet est une distribution sur des mesures de probabilité. UNE mesure de probabilité est une fonction de sous-ensembles d'espace Θ à [0,1]. G est une mesure de probabilité aléatoire distribuée DP, notée , si pour une partition (A₁,…UNE_n) de l'espace Θ on a que .

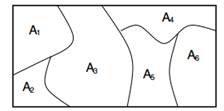
Figure 1: Les marges sur les partitions fi nies sont distribuées en Dirichlet.

Le DP a deux paramètres: Le premier est la distribution de base G₀ qui sert comme un moyen . Le second est le paramètre de force α qui est strictement positif et sert de variance inverse . Il détermine l'étendue de la répétition des valeurs de la distribution de sortie. Plus la valeur de a est élevée, plus la répétition est petite; plus la valeur est petite, plus la répétition des valeurs de la distribution de sortie est élevée. Enfin l'espace Θ est l'espace des paramètres sur lequel on définit le DP. De plus l'espace Θ est aussi l'espace de définition de G₀ qui est le même que celui de G.

Un plus simple et plus manière intuitive pour expliquer un processus Dirichlet est le suivant. Supposons que nous ayons un espace Θ qui peut être partitionné de n'importe quelle manière finie (A₁,…,UNE_n) et une distribution de probabilité G qui leur attribue des probabilités. Le G est une distribution de probabilité spécifique sur Θ mais il y en a beaucoup d'autres. Le processus de Dirichlet sur Θ modélise exactement cela; c'est une distribution sur toutes les distributions de probabilités possibles sur l'espace Θ. Le processus Dirichlet est paramétré avec le G₀ fonction de base et le paramètre de concentration α. On peut dire que G est distribué selon DP avec les paramètres α et G₀ si la distribution conjointe des probabilités que G attribue aux partitions de Θ suit la distribution de Dirichlet. Alternativement, nous pouvons dire que les probabilités que G attribue à toute partition finie de Θ suivent la distribution de Dirichlet.

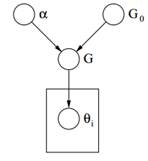
Figure 2: Modèle graphique du processus de Dirichlet

Enfin ci-dessus on peut voir le modèle graphique d'un DP. Notons que α est un hyperparamètre scalaire, G₀ est la distribution de base de DP, G une distribution aléatoire sur Θ l'espace de paramètres échantillonné à partir du DP qui attribue des probabilités aux paramètres et θ_i est un vecteur de paramètres qui est tiré de la distribution G et c'est un élément de l'espace Θ.

2. Processus de Dirichlet postérieur

Les processus de Dirichlet postérieur ont été discutés par Ferguson. Nous commençons par tirer une mesure de probabilité aléatoire G à partir d'un processus de Dirichlet, . Puisque G est une distribution de probabilité sur Θ, nous pouvons également échantillonner à partir de cette distribution et tirer des échantillons indépendants θ à distribution identique₁,…, Θ_n ~ G. Puisque les tirages d'un processus de Dirichlet sont des distributions discrètes, nous pouvons représenter De est une courte notation pour qui est une fonction delta qui prend 1 si et 0 ailleurs. Un effet intéressant de ceci est que puisque G est défini de cette façon, il y a une probabilité positive que différents échantillons aient la même valeur . Comme nous le verrons plus tard, cela crée un effet de clustering qui peut être utilisé pour effectuer une analyse de cluster sur des ensembles de données.

En utilisant les définitions et observations ci-dessus, nous voulons estimer le postérieur du processus de Dirichlet à partir des échantillons θ. Néanmoins puisque nous savons que ainsi que en utilisant les règles de Bayes et la conjugaison entre Dirichlet et Multinomial, nous avons que ainsi que .

Équation 1: Processus de Dirichlet postérieur

Cette propriété est très importante et elle est utilisée par les différentes représentations DP.

3. Représentations du processus de Dirichlet

Dans les segments précédents, nous avons défini le processus de Dirichlet et présenté son modèle théorique. Une question importante à laquelle nous devons répondre est comment savons-nous qu'un tel objet existe et comment nous pouvons construire et représenter un processus Dirichlet.

Les premières indications d'existence ont été fournies par Ferguson qui a utilisé le théorème de cohérence de Kolmogorov, a donné la définition d'un processus de Dirichlet et décrit le processus de Dirichlet postérieur. Poursuivant ses recherches, Blackwell et MacQueen a utilisé le théorème de Finetti pour prouver l'existence d'une telle mesure de probabilité aléatoire et a introduit le schéma d'urne Blackwell-MacQueen qui satisfait les propriétés du processus de Dirichlet. En 1994 Séthuraman fourni un moyen supplémentaire simple et direct de construire un DP en introduisant la construction Stick-break. Enfin, une autre représentation a été fournie par Aldous qui a présenté le Chinese Restaurant Process comme un moyen efficace de construire un Dirichlet Process.

Les différentes représentations du processus de Dirichlet sont mathématiquement équivalentes mais leur formulation diffère car elles examinent le problème sous différents points de vue. Ci-dessous, nous présentons les représentations les plus courantes trouvées dans la littérature et nous nous concentrons sur le processus du restaurant chinois qui fournit un moyen simple et efficace de construire des algorithmes d'inférence pour le processus de Dirichlet.

3.1 Le schéma d'urne Blackwell-MacQueen

Le schéma d'urne Blackwell-MacQueen peut être utilisé pour représenter un processus Dirichlet et il a été introduit par Blackwell et MacQueen. Il est basé sur le schéma de l'urne Pólya qui peut être considéré comme le modèle opposé d'échantillonnage sans remise. Dans le schéma d'urne Pólya, nous supposons que nous avons une urne non transparente contenant des boules colorées et nous tirons des boules au hasard. Quand on dessine une boule, on observe sa couleur, on la remet dans l'urne et on ajoute une boule supplémentaire de la même couleur. Un schéma similaire est utilisé par Blackwell et MacQueen pour construire un processus Dirichlet.

Ce schéma produit une séquence de θ₁, θ₂,… avec probabilités conditionnelles . Dans ce schéma, nous supposons que G₀ est une distribution sur les couleurs et chaque θ_n représente la couleur de la balle qui est placée dans l'urne. le algorithme est comme suit:

· Nous commençons avec une urne vide.

· Avec probabilité proportionnelle à α nous dessinons et nous ajoutons une boule de cette couleur dans l'urne.

· Avec une probabilité proportionnelle à n-1, nous tirons une boule au hasard de l'urne, nous observons sa couleur, nous la remettons dans l'urne et nous ajoutons une boule supplémentaire de la même couleur dans l'urne.

Auparavant, nous avons commencé avec un processus Dirichlet et dérivé le schéma Blackwell-MacQueen. Commençons maintenant à l'envers du schéma Blackwell-MacQueen et dérivons le DP. Puisque θ_i ont été tirées d'une manière iid de G, leur distribution conjointe sera invariante à toute permutation finie et donc elles sont échangeables. Par conséquent, en utilisant le théorème de de Finetti, nous avons qu'il doit exister une distribution sur les mesures pour les rendre iid et cette distribution est le processus de Dirichlet. En conséquence, nous prouvons que le schéma d'urne Blackwell-MacQueen est une représentation de DP et il nous donne un moyen concret de le construire. Comme nous le verrons plus tard, ce schéma est mathématiquement équivalent au Chinese Restaurant Process.

3.2 La construction à rupture de bâton

La construction à rupture de bâton est une manière alternative de représenter un processus Dirichlet qui a été Séthuraman. C'est une manière constructive de former le distribution et utilise le analogie suivante: Nous supposons que nous avons un bâton de longueur 1, nous le cassons en position β₁ et on attribue π₁ égale à la longueur de la partie du bâton que nous avons cassée. Nous répétons le même processus pour obtenir π₂, p₃,… etc; en raison de la façon dont ce schéma est défini, nous pouvons continuer à le faire des fois infinies.

Sur la base de ce qui précède, le π_k peut être modélisé comme , Où le tandis que comme dans les schémas précédents, les θ sont échantillonnés directement par la distribution de base . Par conséquent, la distribution G peut être écrite comme une somme de fonctions delta pondérées avec π_k probabilités égales à . Ainsi, la construction Stick-break nous donne un moyen simple et intuitif de construire un processus de Dirichlet.

3.3 Le processus du restaurant chinois

Le Chinese Restaurant Process, qui a été introduit par Aldous, est un autre moyen efficace de représenter un processus Dirichlet et il peut être directement lié au schéma d'urne Blackwell-MacQueen. Ce schéma utilise le analogie suivante: Nous supposons qu'il existe un restaurant chinois avec une infinité de tables. Lorsque les clients entrent dans le restaurant, ils s'assoient au hasard à l'une des tables occupées ou choisissent de s'asseoir à la première table vide disponible.

Le CRP définit une distribution sur l'espace des partitions des entiers positifs. On commence par dessiner θ₁,… Θ_n du schéma d'urne Blackwell-MacQueen. Comme nous l'avons vu dans les segments précédents, nous nous attendons à voir un effet de regroupement et donc le nombre total de valeurs θ uniques k sera significativement inférieur à n. Ainsi cela définit une partition de l'ensemble {1,2,…, n} en k clusters. Par conséquent, tirer à partir du schéma d'urnes Blackwell-MacQueen induit une partition aléatoire de l'ensemble {1,2,…, n}. Le processus du restaurant chinois est induit distribution sur les partitions. L'algorithme est le suivant:

· Nous commençons avec un restaurant vide.

· La solution 1^st le client s'assoit toujours sur 1^st table

· Le n + 1^th le client a 2 options:

o Asseyez-vous sur la 1ère table inoccupée avec probabilité

o Asseyez-vous sur l'une des kèmes tables occupées avec probabilité
De est le nombre de personnes assises sur cette table

Où α est la valeur de dispersion de DP et n est le nombre total de clients dans le restaurant à un moment donné. La variable latente z_i stocke le numéro de table du i^th client et prend des valeurs de 1 à k_n où k_n est le nombre total de tables occupées lorsque n clients sont dans le restaurant. Il faut noter que le k_n sera toujours inférieur ou égal à n et en moyenne il s'agit de . Notons enfin que la probabilité d'arrangement de la table est invariant aux permutations. Ainsi le z_i est échangeable, ce qui implique que les tables avec la même taille de clients ont la même probabilité.

Le processus du restaurant chinois est étroitement lié au système d'urnes Pólya et au processus Dirichlet. Le CRP est un moyen de spécifier un distribution sur les partitions (affectations de table) de n points et peut être utilisé comme a priori sur l'espace de la variable latente z_i qui détermine les attributions de cluster. Le CRP est équivalent au schéma d'urne de Pólya à la seule différence qu'il n'attribue pas de paramètres à chaque table / cluster. Aller du CRP à l'urne de Pólya nous dessinons pour toutes les tables k = 1,2… puis pour tout x_i qui est regroupé dans le tableau z_i attribuer un . En d'autres termes, attribuez au nouveau x_i le paramètre θ de la table. Enfin depuis nous ne pouvons pas attribuer le θ aux tables infinies depuis le début, nous pouvons simplement assigner un nouveau θ à chaque fois que quelqu'un s'assoit sur une nouvelle table. En raison de tout ce qui précède, le CRP peut nous aider à créer des algorithmes efficaces en termes de calcul pour effectuer une analyse de cluster sur des ensembles de données.

Dans cet article, nous avons discuté du processus Dirichlet et de plusieurs façons de le construire. Nous utiliserons les idées ci-dessus dans le prochain article. Nous présenterons le modèle de mélange de processus Dirichlet et nous utiliserons la représentation du restaurant chinois afin de construire le processus Dirichlet et l'analyse des grappes de préformes. Si vous avez manqué quelques points, ne vous inquiétez pas car les choses commenceront à devenir plus claires avec les deux prochains articles.

J'espère que vous avez trouvé ce post intéressant. Si vous l'avez fait, prenez un moment pour le partager sur Facebook et Twitter. 🙂