Big O jelölések és algoritmusok elemzése Python példákkal

Bevezetés

Általában többféle módon is megoldható a probléma számítógépes program használatával. Például többféleképpen is rendezheti az elemeket egy tömbben – használhatja összevonási rendezés, buborékfajta, beszúrási rendezés, stb. Ezeknek az algoritmusoknak megvannak a maga előnyei és hátrányai, és a fejlesztő feladata, hogy mérlegelje őket, hogy ki tudja választani a legjobb algoritmust, amelyet minden felhasználási esetben használhat. Más szóval, a fő kérdés az, hogy melyik algoritmust kell használni egy adott probléma megoldására, ha több megoldás is létezik a problémára.

Algoritmus elemzés A különböző algoritmusok összetettségének elemzésére és a leghatékonyabb algoritmus megtalálására utal az adott probléma megoldására. Big-O jelölés egy statisztikai mérőszám, amelyet az algoritmus összetettségének leírására használnak.

Ebben az útmutatóban először röviden áttekintjük az algoritmuselemzést, majd mélyebben áttekintjük a Big-O jelölést. Meglátjuk, hogyan használható a Big-O jelölés az algoritmus összetettségének meghatározására különböző Python-függvények segítségével.

Miért fontos az algoritmuselemzés?

Ahhoz, hogy megértsük, miért fontos az algoritmuselemzés, egy egyszerű példát veszünk segítségül. Tegyük fel, hogy egy menedzser feladatot ad két alkalmazottjának, hogy tervezzenek Pythonban egy algoritmust, amely kiszámítja a felhasználó által beírt szám faktoriálisát. Az első alkalmazott által kidolgozott algoritmus így néz ki:

def fact(n):
    product = 1
    for i in range(n):
        product = product * (i+1)
    return product

print(fact(5))

Figyeljük meg, hogy az algoritmus egyszerűen egy egész számot vesz fel argumentumként. Benne fact() nevű változót függvényében product -re van inicializálva 1. A ciklus végrehajtódik innen 1 nak nek n és minden iteráció során az értéket a product megszorozzuk a ciklus által iterált számmal, és az eredményt a rendszer tárolja product ismét változó. A ciklus végrehajtása után a product változó tartalmazza a faktoriálist.

Hasonlóképpen, a második alkalmazott is kifejlesztett egy algoritmust, amely kiszámítja egy szám faktoriálisát. A második alkalmazott rekurzív függvényt használt a szám faktoriálisának kiszámításához n:

def fact2(n):
    if n == 0:
        return 1
    else:
        return n * fact2(n-1)

print(fact2(5))

A menedzsernek kell eldöntenie, hogy melyik algoritmust használja. Ennek érdekében úgy döntöttek, hogy kiválasztják, melyik algoritmus fut gyorsabban. Ennek egyik módja, ha megkeresi a kód végrehajtásához szükséges időt ugyanazon a bemeneten.

A Jupyter notebookban használhatja a %timeit literál, amelyet a függvényhívás követ a függvény végrehajtásához szükséges idő meghatározásához:

%timeit fact(50)

Ez ad nekünk:

9 µs ± 405 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

A kimenet azt mondja, hogy az algoritmus veszi 9 mikroszekundum (plusz/mínusz 45 nanoszekundum) hurkonként.

Hasonlóképpen kiszámíthatjuk, hogy mennyi időbe telik a második megközelítés végrehajtása:

%timeit fact2(50)

Ennek eredménye:

15.7 µs ± 427 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

A második rekurziós algoritmus 15 mikroszekundum (plusz/mínusz 427 nanoszekundum).

A végrehajtási idő azt mutatja, hogy az első algoritmus gyorsabb, mint a rekurziót tartalmazó második algoritmus. Nagy bemenetek esetén a teljesítménykülönbség jelentősebbé válhat.

A végrehajtási idő azonban nem jó mérőszám egy algoritmus összetettségének mérésére, mivel az a hardvertől függ. Egy algoritmushoz objektívebb komplexitáselemzési mérőszámra van szükség. Itt van a Nagy O jelölés jön játszani.

Algoritmus elemzés Big-O jelöléssel

A Big-O jelölés az algoritmus bemenete és az algoritmus végrehajtásához szükséges lépések közötti kapcsolatot jelöli. Ezt egy nagy „O” jelöli, amelyet egy nyitó és záró zárójel követ. A zárójelben a bemenet és az algoritmus által megtett lépések közötti összefüggést az „n” segítségével mutatjuk be.

A legfontosabb dolog az, hogy a Big-O-t nem érdekli a különös példa, amelyben egy algoritmust futtat, mint pl fact(50), hanem azt, hogy milyen jól csinálja skála növekvő bemenettel. Ez sokkal jobb mérőszám az értékeléshez, mint a konkrét idő egy konkrét példányhoz!

Például, ha van a lineáris kapcsolat a bemenet és az algoritmus által a végrehajtás befejezéséhez megtett lépés között a használt Big-O jelölés O (n). Hasonlóképpen a Big-O jelölés is másodfokú függvények is O(n²).

Az intuíció fejlesztése:

• O (n): nál nél n=1, 1 lépés megtörténik. Nál nél n=10, 10 lépés történik.
• O(n²): nál nél n=1, 1 lépés megtörténik. Nál nél n=10, 100 lépés történik.

At n=1, ez a kettő ugyanazt teljesítené! Ez egy másik oka annak, hogy a bemenet és a bemenet feldolgozásához szükséges lépések száma közötti összefüggés megfigyelése jobb, mint a függvények konkrét bemenettel történő kiértékelése.

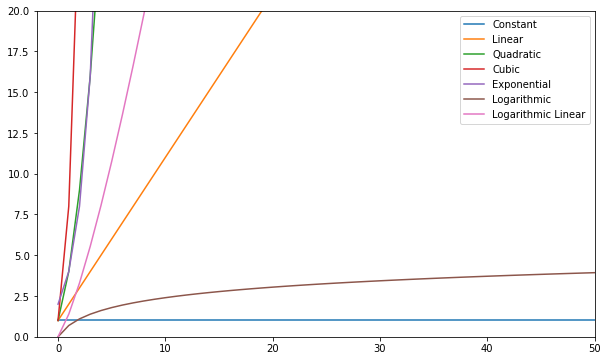
Íme néhány a leggyakoribb Big-O funkciók közül:

Név	Nagy O
Állandó	O(c)
Lineáris	O (n)
Négyzetes	O(n²)
Kocka alakú	O(n³)
Exponenciális	O(2)
Logaritmikus	O(log(n))
Lineáris naplózás	O(nlog(n))

Megjelenítheti ezeket a funkciókat, és összehasonlíthatja őket:

Általánosságban elmondható, hogy minden, ami rosszabb, mint a lineáris, rossz komplexitásnak számít (azaz nem hatékony), és lehetőleg kerülni kell. A lineáris komplexitás rendben van, és általában szükségszerű rossz. A logaritmus jó. A Constant csodálatos!

Ahhoz, hogy képet kapjunk a Big-O kiszámításáról, nézzünk meg néhány példát az állandó, lineáris és kvadratikus bonyolultságra.

Állandó komplexitás - O(C)

Egy algoritmus bonyolultságát állandónak mondjuk, ha az algoritmus végrehajtásához szükséges lépések állandóak maradnak, függetlenül a bemenetek számától. Az állandó bonyolultságot jelöli O(c) ahol c bármilyen állandó szám lehet.

Írjunk Pythonban egy egyszerű algoritmust, amely megkeresi a lista első elemének négyzetét, majd kiírja a képernyőre:

def constant_algo(items):
    result = items[0] * items[0]
    print(result)

constant_algo([4, 5, 6, 8])

A fenti szkriptben a bemeneti mérettől függetlenül, vagy a beviteli lista elemeinek száma items, az algoritmus csak 2 lépést hajt végre:

1. Az első elem négyzetének megkeresése
2. Az eredmény kinyomtatása a képernyőre.

Ezért a komplexitás állandó marad.

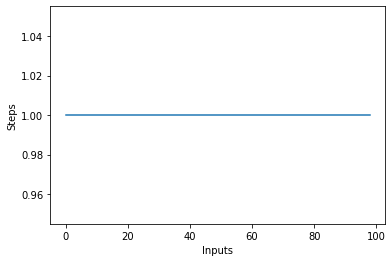
Ha vonalrajzot rajzol a változó méretű items beírva az X tengelyen és a lépések számát az Y tengelyen, akkor egy egyenest kapunk. Készítsünk egy rövid szkriptet, amely segít ennek megjelenítésében. A bemenetek számától függetlenül a végrehajtott lépések száma változatlan marad:

steps = []
def constant(n):
    return 1
    
for i in range(1, 100):
    steps.append(constant(i))
plt.plot(steps)

Lineáris komplexitás - O (n)

Egy algoritmus bonyolultságát lineárisnak nevezzük, ha az algoritmus végrehajtásához szükséges lépések lineárisan nőnek vagy csökkennek a bemenetek számával. A lineáris komplexitást jelöli O (n).

Ebben a példában írjunk egy egyszerű programot, amely a lista összes elemét megjeleníti a konzolon:

def linear_algo(items):
    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

A linear_algo() függvény a fenti példában lineáris, mivel a for-hurok iterációinak száma ez lesz megegyezik a bemenet méretével items sor. Például, ha 4 elem van a items listában a for-ciklus 4-szer kerül végrehajtásra.

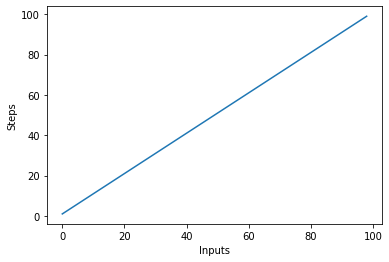
Készítsünk gyorsan egy diagramot a lineáris komplexitási algoritmushoz a bemenetek számával az x tengelyen és a lépések számával az y tengelyen:

steps = []
def linear(n):
    return n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

Ennek eredménye:

Fontos megjegyezni, hogy nagy bemenetek esetén az állandók általában veszítenek értékükből. Ez az oka annak, hogy általában eltávolítjuk a konstansokat a Big-O jelölésből, és az olyan kifejezéseket, mint az O(2n) általában O(n)-re rövidítjük. Az O(2n) és az O(n) is lineáris – a lineáris kapcsolat a lényeg, nem a konkrét érték. Például módosítsuk a linear_algo():

def linear_algo(items):
    for item in items:
        print(item)

    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Két for-hurok van, amelyek ismétlődnek a bemeneten items lista. Így az algoritmus összetettsége válik O(2n), azonban a bemeneti lista végtelen elemei esetén a végtelen kétszerese továbbra is egyenlő a végtelennel. Figyelmen kívül hagyhatjuk az állandót 2 (mivel végső soron jelentéktelen), és az algoritmus összetettsége megmarad O (n).

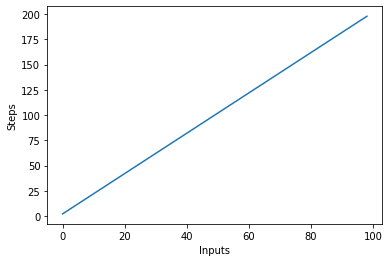
Vizualizáljuk ezt az új algoritmust úgy, hogy ábrázoljuk a bemeneteket az X tengelyen és a lépések számát az Y tengelyen:

steps = []
def linear(n):
    return 2*n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

A fenti forgatókönyvben ez jól látható y=2nazonban a kimenet lineáris, és így néz ki:

Kvadratikus komplexitás - O(n²)

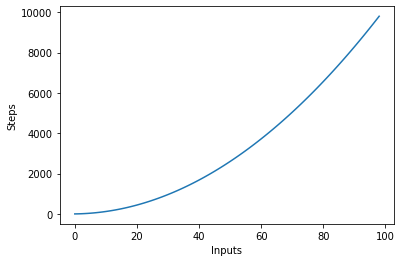
Egy algoritmus összetettségét négyzetesnek nevezzük, ha az algoritmus végrehajtásához szükséges lépések a bemeneti elemek számának másodfokú függvényei. A kvadratikus komplexitást jelöljük O(n²):

def quadratic_algo(items):
    for item in items:
        for item2 in items:
            print(item, ' ' ,item2)

quadratic_algo([4, 5, 6, 8])

Van egy külső ciklusunk, amely a beviteli lista összes elemén keresztül iterál, majd egy beágyazott belső hurok, amely ismét a beviteli lista összes elemén iterál. Az elvégzett lépések teljes száma n*n, ahol n a bemeneti tömb elemeinek száma.

A következő grafikon a bemenetek számát ábrázolja a lépések függvényében egy kvadratikus bonyolultságú algoritmus esetén:

Logaritmikus komplexitás – O (logn)

Egyes algoritmusok logaritmikus komplexitást érnek el, mint pl Bináris keresés. A bináris keresés egy elemet keres egy tömbben, bejelölve a középső egy tömbből, és levágja azt a felét, amelyben az elem nincs. Ezt megismétli a fennmaradó felére, és ugyanazokat a lépéseket folytatja, amíg meg nem találja az elemet. Minden lépésben azt félidőt a tömb elemeinek száma.

Ehhez a tömböt rendezni kell, és feltételeznünk kell az adatokról (például, hogy rendezve vannak).

Ha feltételezéseket tehet a bejövő adatokkal kapcsolatban, akkor olyan lépéseket tehet, amelyek csökkentik az algoritmusok bonyolultságát. A logaritmikus komplexitás kívánatos, mivel még nagy skálázású bemenettel is jó teljesítményt ér el.

Megtalálni az összetett függvények összetettségét?

A korábbi példákban meglehetősen egyszerű függvények voltak a bemeneten. De hogyan számítjuk ki a függvények Big-O-ját, amelyek (több) más függvényt hívnak meg a bemeneten?

Vessen egy pillantást:

def complex_algo(items):

    for i in range(5):
        print("Python is awesome")

    for item in items:
        print(item)

    for item in items:
        print(item)

    print("Big O")
    print("Big O")
    print("Big O")

complex_algo([4, 5, 6, 8])

A fenti szkriptben számos feladatot hajtanak végre, először egy karakterláncot ötször nyomtatnak ki a konzolon a print nyilatkozat. Ezután kétszer nyomtatjuk ki a képernyőre a beviteli listát, végül háromszor egy másik karakterláncot nyomtatunk ki a konzolon. Egy ilyen algoritmus bonyolultságának megállapításához az algoritmus kódját részekre kell bontani, és meg kell próbálnunk megtalálni az egyes darabok összetettségét. Jelölje meg az egyes darabok összetettségét.

Az első részben a következőket találjuk:

for i in range(5):
	print("Python is awesome")

Ennek a résznek a bonyolultsága az O (5) mivel ebben a kódrészletben a bemenettől függetlenül öt állandó lépést hajtanak végre.

Következő:

for item in items:
	print(item)

Tudjuk, hogy a fenti kódrészlet bonyolult O (n). Hasonlóképpen a következő kódrészlet összetettsége is O (n):

for item in items:
	print(item)

Végül a következő kódrészletben egy karakterlánc háromszor kerül kinyomtatásra, ezért a bonyolultság az O (3):

print("Big O")
print("Big O")
print("Big O")

Az általános összetettség megállapításához egyszerűen hozzá kell adnunk a következő egyedi összetettségeket:

O(5) + O(n) + O(n) + O(3)

A fentieket leegyszerűsítve a következőket kapjuk:

O(8) + O(2n) = O(8+2n)

Korábban azt mondtuk, hogy amikor a bemenet (amelynek hosszúsága ebben az esetben n) rendkívül nagy lesz, akkor az állandók jelentéktelenek, azaz a végtelen kétszer vagy fele továbbra is végtelen marad. Ezért figyelmen kívül hagyhatjuk az állandókat. Az algoritmus végső összetettsége az lesz O (n)!

A legrosszabb vs legjobb eset összetettsége

Általában, ha valaki egy algoritmus bonyolultságáról kérdez, a legrosszabb eset bonyolultsága (Big-O) érdekli. Néha a legjobb eset összetettsége is érdekelheti őket (Big-Omega).

A kettő közötti kapcsolat megértéséhez vessünk egy pillantást egy másik kódrészletre:

def search_algo(num, items):
    for item in items:
        if item == num:
            return True
        else:
            pass
nums = [2, 4, 6, 8, 10]

print(search_algo(2, nums))

A fenti szkriptben van egy függvényünk, amely bemenetként egy számot és egy számlistát vesz fel. Igazat ad vissza, ha az átadott szám megtalálható a számlistában, ellenkező esetben visszaadja None. Ha 2-re keres a listában, akkor az első összehasonlításban megtalálja. Ez az algoritmus legjobb összetettsége, mivel a keresett elem az első keresett indexben található. A legjobb eset összetettsége, ebben az esetben az O (1). Másrészt, ha 10-et keresel, akkor az utoljára keresett indexnél lesz megtalálva. Az algoritmusnak tehát át kell keresnie a lista összes elemét a legrosszabb eset bonyolultsága válik O (n).

A legjobb és legrosszabb eset bonyolultsága mellett kalkulálhat is az átlagos komplexitás (Big-Theta) egy algoritmus, amely megmondja, hogy "egy véletlen bemenet mellett mekkora az algoritmus várható időbonyolultsága"?

Tér komplexitás

Az időbonyolítás mellett, ahol megszámolja az algoritmus végrehajtásához szükséges lépések számát, megtalálhatja a tér összetettsége amely a program végrehajtása során a memóriában lefoglalandó terület nagyságára vonatkozik.

Vessen egy pillantást a következő példára:

def return_squares(n):
    square_list = []
    for num in n:
        square_list.append(num * num)

    return square_list

nums = [2, 4, 6, 8, 10]
print(return_squares(nums))

A return_squares() függvény elfogadja az egész számok listáját, és egy listát ad vissza a megfelelő négyzetekkel. Az algoritmusnak ugyanannyi elem számára kell memóriát lefoglalnia, mint a bemeneti listában. Ezért az algoritmus térbonyolultsága válik O (n).

Következtetés

A Big-O jelölés az algoritmus összetettségének mérésére használt szabványos mérőszám. Ebben az útmutatóban azt tanulmányoztuk, hogy mi az a Big-O jelölés, és hogyan használható különféle algoritmusok összetettségének mérésére. Különböző típusú Big-O függvényeket is tanulmányoztunk különböző Python-példák segítségével. Végül röviden áttekintettük a legrosszabb és legjobb eset bonyolultságát, valamint a tér összetettségét.