Végleges útmutató a K-Means klaszterezéshez a Scikit-Learn segítségével

Bevezetés

K-Means klaszterezés az egyik legszélesebb körben használt felügyelt gépi tanulási algoritmus, amely az adatpéldányok közötti hasonlóság alapján adatklasztereket képez.

Ebben az útmutatóban először egy egyszerű példát veszünk szemügyre, hogy megértsük, hogyan működik a K-Means algoritmus, mielőtt a Scikit-Learn segítségével implementáljuk. Ezután megvitatjuk, hogyan határozhatjuk meg a klaszterek számát (Ks) a K-Means-ben, és kitérünk a távolságmérőkre, a szórásra és a K-Means előnyeire és hátrányaira is.

Motiváció

Képzelje el a következő helyzetet. Egy nap, amikor a környéken járkált, észrevette, hogy 10 kisbolt van, és elkezdett azon tűnődni, hogy melyik üzletek hasonlítanak egymáshoz – közelebb egymáshoz. Miközben a kérdés megválaszolásának módjait kereste, egy érdekes megközelítésre bukkant, amely a térképen lévő koordinátáik alapján csoportokra osztja az üzleteket.

Például, ha egy üzlet 5 km-re nyugatra és 3 km-re északra található, akkor hozzá kell rendelnie (5, 3) koordinálja, és ábrázolja grafikonon. Ábrázoljuk ezt az első pontot, hogy elképzeljük, mi történik:

import matplotlib.pyplot as plt

plt.title("Store With Coordinates (5, 3)")
plt.scatter(x=5, y=3)

Ez még csak az első pont, így képet kaphatunk arról, hogyan képviselhetünk egy üzletet. Tegyük fel, hogy már van 10 koordinátánk az összegyűjtött 10 üzlethez. Miután megszerveztük őket a numpy tömbben ábrázolhatjuk a helyüket is:

import numpy as np

points = np.array([[5, 3], [10, 15], [15, 12], [24, 10], [30, 45], [85, 70], [71, 80], [60, 78], [55, 52],[80, 91]])

xs = points[:,0] 
ys = points[:,1]  

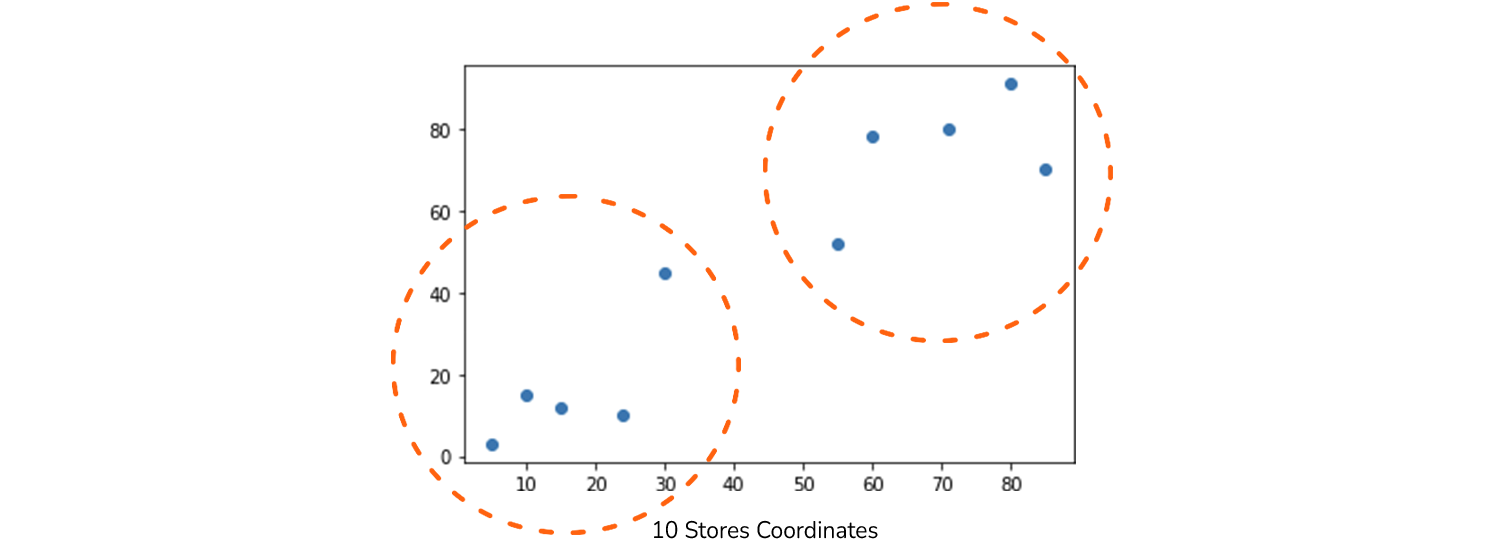
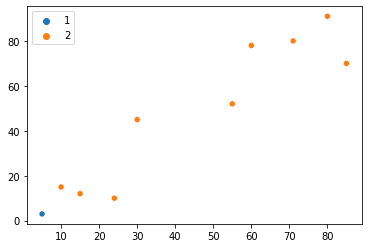
plt.title("10 Stores Coordinates")
plt.scatter(x=xs, y=ys)

A K-Means algoritmus manuális megvalósítása

Most megnézhetjük a 10 üzletet egy grafikonon, és a fő probléma az, hogy megtaláljuk-e azt a módot, hogy a közelség alapján különböző csoportokba sorolhatók-e? Ha gyorsan megnézzük a grafikont, valószínűleg észrevesszük két üzletcsoport – az egyik a bal alsó pontok, a másik pedig a jobb felső pontok. Talán még külön csoportként is megkülönböztethetjük a középen lévő két pontot – így létrehozva három különböző csoport.

Ebben a részben áttekintjük a pontok manuális klaszterezésének folyamatát – adott számú csoportra osztva. Így lényegében gondosan végigmegyünk az összes lépésen K-Means klaszterező algoritmus. Ennek a szakasznak a végére intuitív és gyakorlati ismereteket szerez a K-Means klaszterezés során végrehajtott összes lépésről. Ezt követően átadjuk a Scikit-Learn-nek.

Mi lenne a legjobb módja annak meghatározására, hogy két vagy három pontcsoport van-e? Az egyik egyszerű módszer az lenne, ha egyszerűen kiválaszt egy számú csoportot – például kettőt –, majd megpróbálja a pontok csoportosítását a választás alapján.

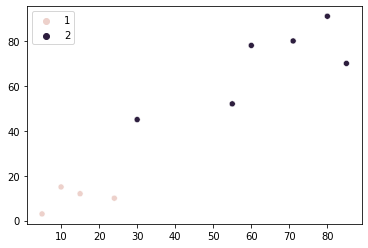
Tegyük fel, hogy úgy döntöttünk, hogy vannak két csoport üzleteinkből (pontok). Most meg kell találnunk a módját annak megértésére, hogy mely pontok melyik csoporthoz tartoznak. Ezt úgy teheti meg, hogy kiválaszt egy pontot a reprezentációhoz 1 csoport és egyet képviselni 2 csoport. Ezeket a pontokat referenciaként fogják használni az egyes csoportok összes többi pontjától való távolság mérésénél.

Ilyen módon mondd el a pontot (5, 3) végül az 1. csoportba tartozik, és pont (79, 60) csoportba 2. Amikor új pontot próbálunk kijelölni (6, 3) csoportokhoz, meg kell mérnünk a távolságát attól a két ponttól. A pont esetében (6, 3) is közelebb hoz (5, 3), ezért az adott pont által képviselt csoportba tartozik - 1 csoport. Így könnyen csoportosíthatjuk az összes pontot megfelelő csoportokba.

Ebben a példában a csoportok számának meghatározása mellett (klaszterek) – szintén kiválasztunk néhány pontot, hogy a referencia távolságot az egyes csoportok új pontjaiért.

Ez az általános elképzelés, hogy megértsük az üzleteink közötti hasonlóságokat. Alkalmazzuk a gyakorlatba – először kiválaszthatjuk a két referenciapontot véletlen. A referenciapont 1 csoport lesz (5, 3) és a referenciapontja 2 csoport lesz (10, 15). Mindkét pontot kiválaszthatjuk numpy tömb által [0] és a [1] indexeket, és tárolja azokat g1 (1. csoport) és g2 (2. csoport) változók:

g1 = points[0]
g2 = points[1]

Ezt követően ki kell számítanunk az összes többi pont és az adott referenciapont közötti távolságot. Ez felvet egy fontos kérdést – hogyan mérjük ezt a távolságot. Lényegében bármilyen távolságmértéket használhatunk, de ebben az útmutatóban használjuk az euklideszi távolságot_.

Hasznos lehet tudni, hogy az euklideszi távolságmérés Pythagoras tételén alapul:

$$
c^2 = a^2 + b^2
$$

A síkban lévő pontokhoz alkalmazkodva - (a1, b1) és a (a2, b2), az előző képlet a következőképpen alakul:

$$
c^2 = (a2-a1)^2 + (b2-b1)^2
$$

A távolság négyzetgyöke lesz c, így a képletet így is felírhatjuk:

$$
euklideszi_{dist} = sqrt[2][(a2 – a1)^2 + (b2 – b1) ^2)]
$$

Eddig a pontokat választottuk ki a csoportok képviseletére, és tudjuk, hogyan számoljuk ki a távolságokat. Most pedig állítsuk össze a távolságokat és a csoportokat úgy, hogy minden egyes összegyűjtött bolti pontot hozzárendelünk egy csoporthoz.

Ennek jobb megjelenítéséhez három listát adunk meg. Aki először tárolja az első csoport pontjait – points_in_g1. A második, aki pontokat tárol a 2. csoportból – points_in_g2és az utolsó – group, Hogy címke a pontokat akár 1 (1. csoportba tartozik) ill 2 (a 2-es csoportba tartozik):

points_in_g1 = []
points_in_g2 = []
group = []

Most ismételhetjük a pontjainkat, és kiszámíthatjuk az euklideszi távolságot közöttük és az egyes csoporthivatkozásaink között. Minden pont az lesz közelebb két csoport egyikéhez – attól függően, hogy melyik csoport van a legközelebb, minden pontot hozzárendelünk a megfelelő listához, miközben hozzáadjuk 1 or 2 hoz group lista:

for p in points:
    x1, y1 = p[0], p[1]
    euclidean_distance_g1 = np.sqrt((g1[0] - x1)**2 + (g1[1] - y1)**2)
    euclidean_distance_g2 = np.sqrt((g2[0] - x1)**2 + (g2[1] - y1)**2)
    if euclidean_distance_g1 < euclidean_distance_g2:
        points_in_g1.append(p)
        group.append('1')
    else:
        points_in_g2.append(p)
        group.append('2')

Nézzük meg ennek az iterációnak az eredményeit, hogy lássuk, mi történt:

print(f'points_in_g1:{points_in_g1}n 
npoints_in_g2:{points_in_g2}n 
ngroup:{group}')

Aminek eredménye:

points_in_g1:[array([5, 3])]
 
points_in_g2:[array([10, 15]), array([15, 12]), 
              array([24, 10]), array([30, 45]), 
              array([85, 70]), array([71, 80]),
              array([60, 78]), array([55, 52]), 
              array([80, 91])]
 
group:[1, 2, 2, 2, 2, 2, 2, 2, 2, 2] 

A klaszterezés eredményét a hozzárendelt csoportok alapján különböző színekkel is ábrázolhatjuk, a Seaborn's segítségével scatterplot() a ... val group mint hue érv:

import seaborn as sns

sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

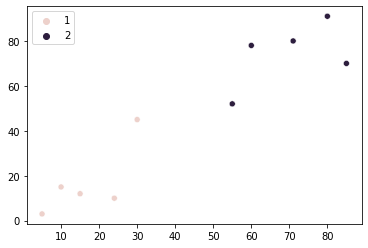
Jól látható, hogy csak az első pontunk van az 1. csoporthoz, az összes többi pont pedig a 2. csoporthoz. Ez az eredmény eltér attól, amit az elején elképzeltünk. Figyelembe véve az eredményeink és a kezdeti várakozásaink közötti különbséget – van-e mód ezen változtatni? Úgy tűnik, van!

Az egyik megközelítés az, hogy megismételjük a folyamatot, és különböző pontokat választunk a csoportok hivatkozási alapjául. Remélhetőleg ez megváltoztatja az eredményeinket, jobban összhangban azzal, amit az elején elképzeltünk. A második alkalommal nem véletlenszerűen választhattuk ki őket, mint korábban, hanem úgy, hogy megkaptuk a jelent az összes már csoportosított pontunk közül. Így ezek az új pontok a megfelelő csoportok közepére kerülhetnek.

Például, ha a második csoportnak csak pontjai voltak (10, 15), (30, 45). Az új központi pont az lenne (10 + 30)/2 és a (15+45)/2 – ami egyenlő azzal (20, 30).

Mivel az eredményeinket listákba helyeztük, először konvertálhatjuk azokat numpy tömböket, válassza ki az x-eket, ys-eket, majd szerezze be a jelent:

g1_center = [np.array(points_in_g1)[:, 0].mean(), np.array(points_in_g1)[:, 1].mean()]
g2_center = [np.array(points_in_g2)[:, 0].mean(), np.array(points_in_g2)[:, 1].mean()]
g1_center, g2_center

Annak érdekében, hogy megismételjük a folyamatot új középpontjainkkal, alakítsuk át a korábbi kódunkat függvényré, futtassuk le, és nézzük meg, történt-e változás a pontok csoportosításában:

def assigns_points_to_two_groups(g1_center, g2_center):
    points_in_g1 = []
    points_in_g2 = []
    group = []

    for p in points:
        x1, y1 = p[0], p[1]
        euclidean_distance_g1 = np.sqrt((g1_center[0] - x1)**2 + (g1_center[1] - y1)**2)
        euclidean_distance_g2 = np.sqrt((g2_center[0] - x1)**2 + (g2_center[1] - y1)**2)
        if euclidean_distance_g1 < euclidean_distance_g2:
            points_in_g1.append(p)
            group.append(1)
        else:
            points_in_g2.append(p)
            group.append(2)
    return points_in_g1, points_in_g2, group

Hívjuk meg a függvényt, és tároljuk az eredményét points_in_g1, points_in_g2és group változók:

points_in_g1, points_in_g2, group = assigns_points_to_two_groups(g1_center, g2_center)
points_in_g1, points_in_g2, group

Illetve ábrázolja a szórást a színes pontokkal a csoportfelosztás megjelenítéséhez:

sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

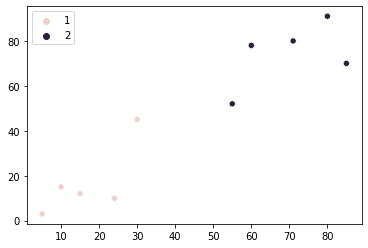
Úgy tűnik, pontjaink csoportosítása az javulni. Ennek ellenére van két pont a grafikon közepén, amelyek bármelyik csoporthoz hozzárendelhetők, ha figyelembe vesszük a két csoporthoz való közelségüket. Az általunk eddig kifejlesztett algoritmus mindkét pontot a második csoporthoz rendeli.

Ez azt jelenti, hogy a folyamatot valószínűleg még egyszer megismételhetjük az X-ek és Y-k átlagával, két új központi pontot létrehozva (centroidok) csoportjainkra, és a távolság alapján újra hozzárendeljük őket.

Hozzunk létre egy függvényt is a centroidok frissítésére. Az egész folyamat most ennek a függvénynek a többszöri meghívására redukálható:

def updates_centroids(points_in_g1, points_in_g2):
    g1_center = np.array(points_in_g1)[:, 0].mean(), np.array(points_in_g1)[:, 1].mean()
    g2_center = np.array(points_in_g2)[:, 0].mean(), np.array(points_in_g2)[:, 1].mean()
    return g1_center, g2_center

g1_center, g2_center = updates_centroids(points_in_g1, points_in_g2)
points_in_g1, points_in_g2, group = assigns_points_to_two_groups(g1_center, g2_center)
sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

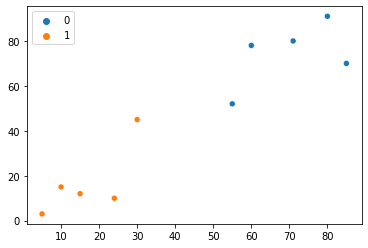
Figyeljük meg, hogy a harmadik iteráció után minden egyes pont más-más klaszterhez tartozik. Úgy tűnik, az eredmények egyre jobbak – tegyük meg még egyszer. Most megy a negyedik iteráció a mi módszerünkből:

g1_center, g2_center = updates_centroids(points_in_g1, points_in_g2)
points_in_g1, points_in_g2, group = assigns_points_to_two_groups(g1_center, g2_center)
sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

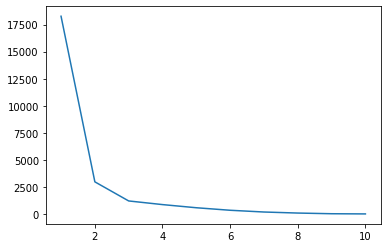
Negyedszer kaptunk ugyanaz az eredmény mint az előző. Így úgy tűnik, a pontjaink már nem fognak csoportot váltani, eredményünk elért valamiféle stabilitást – megváltoztathatatlan állapotba került, ill. konvergens. Ezen kívül pontosan ugyanazt az eredményt kaptuk, mint amit a két csoport esetében elképzeltünk. Azt is láthatjuk, hogy van-e értelme ennek az elért felosztásnak.

Röviden összegezzük az eddigieket. 10 üzletünket földrajzilag két részre osztottuk – az egyik az alsó délnyugati régiókban, a másik pedig az északkeleti részekben. Érdekes lehet a már meglévő adatokon kívül még több adatot gyűjteni – bevétel, napi ügyfélszám és még sok más. Így gazdagabb elemzést végezhetünk, és esetleg érdekesebb eredményeket generálhatunk.

Az ehhez hasonló klaszterezési tanulmányok akkor végezhetők el, ha egy már kialakult márka szeretne egy területet kiválasztani egy új üzlet megnyitásához. Ebben az esetben a hely mellett sokkal több változót is figyelembe veszünk.

Mi köze van ennek a K-Means algoritmushoz?

Miközben ezeket a lépéseket követte, azon töprenghetett, mi közük van ezeknek a K-Means algoritmushoz. Az általunk eddig lefolytatott folyamat a K-Means algoritmus. Röviden: meghatároztuk a csoportok/klaszterek számát, véletlenszerűen választottuk ki a kezdeti pontokat, és frissítettük a centroidokat minden iterációban, amíg a klaszterek nem konvergáltak. A teljes algoritmust alapvetően kézzel végeztük – minden lépést gondosan végrehajtva.

A K a K-Means a klaszterek száma amelyeket be kell állítani az iterációs folyamat megkezdése előtt. A mi esetünkben K = 2. Ezt a jellemzőt néha úgy tekintik negatív Figyelembe véve, hogy vannak más klaszterezési módszerek is, például a hierarchikus fürtözés, amelyekhez nem szükséges előre rögzített számú fürt.

Eszközhasználata miatt a K-közép is válik érzékeny a kiugró értékekre és a szélsőséges értékekre – fokozzák a változékonyságot, és megnehezítik centroidjaink szerepét. Tehát legyen tudatában annak, hogy teljesíteni kell szélsőséges értékek és kiugró elemzés mielőtt klaszterezést végezne a K-Means algoritmus segítségével.

Figyeljük meg azt is, hogy pontjainkat egyenes részekre tagoltuk, a klaszterek létrehozásakor nincsenek görbék. Ez a K-Means algoritmus hátránya is lehet.

A K-Means-nek is sok van előnyei! Jól teljesít rajta nagy adatkészletek ami nehezen kezelhető lehet, ha bizonyos típusú hierarchikus klaszterezési algoritmusokat használ. Az is konvergenciát garantál, és könnyen általánosítani és a alkalmazkodni. Emellett valószínűleg ez a leggyakrabban használt klaszterező algoritmus.

Most, hogy végignéztük a K-Means algoritmus összes lépését, és megértettük annak előnyeit és hátrányait, végre megvalósíthatjuk a K-Meanst a Scikit-Learn könyvtár segítségével.

A K-Means algoritmus implementálása scikit-learn

Az eredmény ellenőrzéséhez hajtsuk végre újra ezt a folyamatot, de most 3 sornyi kóddal sklearn:

from sklearn.cluster import KMeans


kmeans = KMeans(n_clusters=2, random_state=42) 
kmeans.fit(points)
kmeans.labels_

Itt a címkék megegyeznek az előző csoportjainkkal. Gyorsan ábrázoljuk az eredményt:

sns.scatterplot(x = points[:,0], y = points[:,1], hue=kmeans.labels_)

Az eredményül kapott diagram megegyezik az előző szakaszban szereplővel.

A Scikit-Learn segítségével a K-Means inicializálható is a gyorsabb konvergencia érdekében a init='k-means++' érv. Tágabb értelemben K-Means++ továbbra is a k kezdeti klaszterközpontok véletlenszerűen, egyenletes eloszlást követve. Ezután minden egyes következő klaszterközéppontot nem csak távolságmérték kiszámításával választunk ki a fennmaradó adatpontok közül, hanem a valószínűség segítségével. A valószínűség használata felgyorsítja az algoritmust, és nagyon nagy adatkészletek kezelésekor hasznos.

A könyök módszer – A csoportok legjobb számának kiválasztása

Eddig jó! 10 üzletet csoportosítottunk a pontok és a centroidok közötti euklideszi távolság alapján. De mi a helyzet azzal a két ponttal a grafikon közepén, amelyeket egy kicsit nehezebb klaszterezni? Nem lehetne ők is külön csoportot alkotni? Tényleg hibáztunk a választással? K = 2 csoportok? Talán tényleg volt K = 3 csoportok? Akár háromnál több csoportunk is lehet, és nem tudtunk róla.

Az itt feltett kérdés az hogyan határozzuk meg a csoportok számát (K) a K-Meansben. A kérdés megválaszolásához meg kell értenünk, hogy létezik-e „jobb” klaszter egy másik K értékhez.

A naiv módszer ennek kiderítésére a különböző értékekkel rendelkező pontok csoportosítása K, így K=2, K=3, K=4 és így tovább:

for number_of_clusters in range(1, 11): 
    kmeans = KMeans(n_clusters = number_of_clusters, random_state = 42)
    kmeans.fit(points) 

De a különböző pontok csoportosítása Ks kizárólag nem lesz elég hogy megértsük, az ideális értéket választottuk-e K. Szükségünk van egy módra, hogy értékeljük a klaszterezés minőségét mindegyik esetében K választottunk.

Kézi számítása a Klaszteren belüli négyzetösszeg (WCSS)

Itt az ideális hely annak mérésére, hogy a csoportosított pontjaink mennyire vannak közel egymáshoz. Lényegében leírja, hogy mennyi variancia egyetlen klaszteren belül van. Ezt az intézkedést ún A klaszter négyzetösszegén belülvagy WCSS röviden. Minél kisebb a WCSS, annál közelebb vannak a pontjaink, így egy jobban formált klasztert kapunk. A WCSS képlet tetszőleges számú klaszterhez használható:

$$
WCSS = összeg(Pi_1 – Centroid_1)^2 + cdots + összeg(Pi_n – Centroid_n)^2
$$

Most feltételezhetjük, hogy két klaszter mellett döntöttünk, és megpróbáljuk megvalósítani a WCSS-t, hogy jobban megértsük, mi a WCSS és hogyan kell használni. A képlet szerint össze kell foglalnunk az összes klaszterpont és súlypont közötti különbségek négyzetét. Tehát, ha az első pontunk az első csoportból az (5, 3) és az első csoport utolsó centroidja (konvergencia után) az (16.8, 17.0), a WCSS a következő lesz:

$$
WCSS = összeg((5,3) – (16.8, 17.0))^2
$$

$$
WCSS = összeg((5-16.8) + (3-17.0))^2
$$

$$
WCSS = összeg((-11.8) + (-14.0))^2
$$

$$
WCSS = összeg((-25.8))^2
$$

$$
WCSS = 335.24
$$

Ez a példa bemutatja, hogyan számítjuk ki a WCSS-t a fürt egy pontjára. De a klaszter általában egynél több pontot tartalmaz, és mindegyiket figyelembe kell vennünk a WCSS kiszámításakor. Ezt úgy fogjuk megtenni, hogy meghatározunk egy függvényt, amely pontokból és súlypontokból álló klasztert kap, és a négyzetek összegét adja vissza:

def sum_of_squares(cluster, centroid):
    squares = []
    for p in cluster:
        squares.append((p - centroid)**2)
        ss = np.array(squares).sum()
    return ss

Most megkapjuk az egyes klaszterek négyzeteinek összegét:

g1 = sum_of_squares(points_in_g1, g1_center)
g2 = sum_of_squares(points_in_g2, g2_center)

És összegezze az eredményeket, hogy megkapja a végösszeget WCSS:

g1 + g2

Ennek eredményeként:

2964.3999999999996

Tehát a mi esetünkben mikor K egyenlő 2-vel, a teljes WCSS 2964.39. Most válthatunk Ks-t, és mindegyikre kiszámolhatjuk a WCSS-t. Így betekintést nyerhetünk abba, hogy mi K úgy kell döntenünk, hogy klaszterezésünk a legjobban teljesítsen.

Számító WCSS <p></p> scikit-learn

Szerencsére nem kell manuálisan kiszámítanunk a WCSS-t mindegyikhez K. Miután elvégeztük a K-Means klaszterezést az adott számú klaszterre, a WCSS-t a inertia_ tulajdonság. Most visszatérhetünk a K-Means-hez for hurkot, használja a fürtök számának megadásához, és a megfelelő WCSS-értékek felsorolásához:

wcss = [] 
for number_of_clusters in range(1, 11): 
    kmeans = KMeans(n_clusters = number_of_clusters, random_state = 42)
    kmeans.fit(points) 
    wcss.append(kmeans.inertia_)
wcss

Figyelje meg, hogy a lista második értéke pontosan ugyanaz, mint amit korábban kiszámítottunk K = 2:

[18272.9, # For k=1 
 2964.3999999999996, # For k=2
 1198.75, # For k=3
 861.75,
 570.5,
 337.5,
 175.83333333333334,
 79.5,
 17.0,
 0.0]

Az eredmények vizualizálásához vázoljuk fel az eredményeket Ks a WCSS értékekkel együtt:

ks = [1, 2, 3, 4, 5 , 6 , 7 , 8, 9, 10]
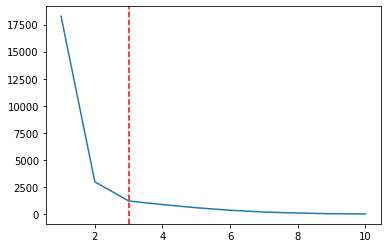
plt.plot(ks, wcss)

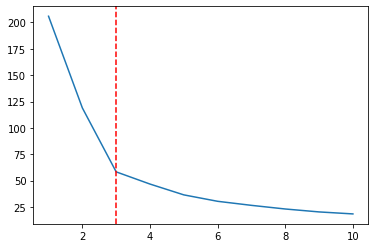
Megszakítás van egy telken, amikor x = 2, egy mélypont a sorban, és egy még alacsonyabb, amikor x = 3. Figyeljük meg, hogy emlékeztet bennünket a egy könyök alakja. A Ks-t a WCSS-sel együtt ábrázolva a Könyök módszer a Ks szám kiválasztásához. És a választott K pontosan a legalacsonyabb könyökpont, szóval az lenne 3 helyett 2, a mi esetünkben:

ks = [1, 2, 3, 4, 5 , 6 , 7 , 8, 9, 10]
plt.plot(ks, wcss);
plt.axvline(3, linestyle='--', color='r')

Újra lefuttathatjuk a K-Means fürt algoritmust, hogy megnézzük, hogyan néznek ki adataink három klaszter:

kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(points)
sns.scatterplot(x = points[:,0], y = points[:,1], hue=kmeans.labels_)

Már két klaszterrel is elégedettek voltunk, de a könyök módszer szerint három klaszter jobban passzolna az adatainkhoz. Ebben az esetben kettő helyett háromféle üzletünk lenne. A könyökös módszer alkalmazása előtt a délnyugati és északkeleti üzletcsoportokra gondoltunk, most már a központban is vannak üzleteink. Talán ez jó hely lehet egy másik üzlet nyitására, mivel kevesebb verseny lenne a közelben.

Alternatív klaszterminőségi intézkedések

Vannak más mérőszámok is, amelyek a klaszter minőségének értékeléséhez használhatók:

• Silhouette Score – nemcsak a klaszteren belüli pontok közötti távolságot elemzi, hanem magukat a klasztereket is
• Klaszterek között Négyzetösszeg (BCSS) – a WCSS-t kiegészítő metrika
• Négyzetösszeg hiba (SSE)
• Maximális sugár – méri a legnagyobb távolságot egy ponttól a súlypontig
• Átlagos sugár – a pont és a súlypont közötti legnagyobb távolság összege osztva a klaszterek számával.

Javasoljuk, hogy mindegyiket kísérletezzen és ismerje meg, mivel a problémától függően néhány alternatíva jobban alkalmazható, mint a legszélesebb körben használt mérőszámok (WCSS és Silhouette pontszám).

Végül, mint sok adattudományi algoritmus esetében, szeretnénk csökkenteni az egyes klasztereken belüli szórást, és maximalizálni a különböző klaszterek közötti eltérést. Tehát több meghatározott és elkülöníthető klaszterünk van.

A K-Means alkalmazása egy másik adatkészletre

Használjuk a tanultakat egy másik adathalmazban. Ezúttal megpróbálunk hasonló borokból álló csoportokat találni.

Az importálással kezdjük pandas hogy elolvassa a wine-clustering CSV (vesszővel elválasztott értékek) fájlba a Dataframe szerkezet:

import pandas as pd

df = pd.read_csv('wine-clustering.csv')

Betöltés után nézzük meg az első öt adatrekordot a head() eljárás:

df.head()

Ennek eredményeként:

	Alcohol 	Malic_Acid 	Ash 	Ash_Alcanity 	Magnesium 	Total_Phenols 	Flavanoids 	Nonflavanoid_Phenols 	Proanthocyanins 	Color_Intensity 	Hue 	OD280 	Proline
0 	14.23 		1.71 		2.43 	15.6 			127 		2.80 			3.06 		0.28 					2.29 				5.64 				1.04 	3.92 	1065
1 	13.20 		1.78 		2.14 	11.2 			100 		2.65 			2.76 		0.26 					1.28 				4.38 				1.05 	3.40 	1050
2 	13.16 		2.36 		2.67 	18.6 			101 		2.80 			3.24 		0.30 					2.81 				5.68 				1.03 	3.17 	1185
3 	14.37 		1.95 		2.50 	16.8 			113 		3.85 			3.49 		0.24 					2.18 				7.80 				0.86 	3.45 	1480
4 	13.24 		2.59 		2.87 	21.0 			118 		2.80 			2.69 		0.39 					1.82 				4.32 				1.04 	2.93 	735

Számos mérést végeztünk a borokban lévő anyagokról. Itt szintén nem kell átalakítanunk a kategorikus oszlopokat, mert mindegyik numerikus. Most pedig vessünk egy pillantást a leíró statisztikákra a describe() eljárás:

df.describe().T 

A leíró táblázat:

 						count 	mean 		std 		min 	25% 	50% 	75% 		max
Alcohol 				178.0 	13.000618 	0.811827 	11.03 	12.3625 13.050 	13.6775 	14.83
Malic_Acid 				178.0 	2.336348 	1.117146 	0.74 	1.6025 	1.865 	3.0825 		5.80
Ash 					178.0 	2.366517 	0.274344 	1.36 	2.2100 	2.360 	2.5575 		3.23
Ash_Alcanity 			178.0 	19.494944 	3.339564 	10.60 	17.2000 19.500 	21.5000 	30.00
Magnesium 				178.0 	99.741573 	14.282484 	70.00 	88.0000 98.000 	107.0000 	162.00
Total_Phenols 			178.0 	2.295112 	0.625851 	0.98 	1.7425 	2.355 	2.8000 		3.88
Flavanoids 				178.0 	2.029270 	0.998859 	0.34 	1.2050 	2.135 	2.8750 		5.08
Nonflavanoid_Phenols 	178.0 	0.361854 	0.124453 	0.13 	0.2700 	0.340 	0.4375 		0.66
Proanthocyanins 		178.0 	1.590899 	0.572359 	0.41 	1.2500 	1.555 	1.9500 		3.58
Color_Intensity 		178.0 	5.058090 	2.318286 	1.28 	3.2200 	4.690 	6.2000 		13.00
Hue 					178.0 	0.957449 	0.228572 	0.48 	0.7825 	0.965 	1.1200 		1.71
OD280 					178.0 	2.611685 	0.709990 	1.27 	1.9375 	2.780 	3.1700 		4.00
Proline 				178.0 	746.893258 	314.907474 	278.00 	500.500 673.500 985.0000 	1680.00

A táblázatot nézve egyértelmű, hogy van néhány változékonyság az adatokban – egyes oszlopokhoz, mint pl Alchool van több, és mások számára, mint pl Malic_Acid, Kevésbé. Most ellenőrizhetjük, hogy vannak-e ilyenek nullvagy NaN értékek az adatkészletünkben:

df.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 178 entries, 0 to 177
Data columns (total 13 columns):
 #   Column                Non-Null Count  Dtype  
---  ------                --------------  -----  
 0   Alcohol               178 non-null    float64
 1   Malic_Acid            178 non-null    float64
 2   Ash                   178 non-null    float64
 3   Ash_Alcanity          178 non-null    float64
 4   Magnesium             178 non-null    int64  
 5   Total_Phenols         178 non-null    float64
 6   Flavanoids            178 non-null    float64
 7   Nonflavanoid_Phenols  178 non-null    float64
 8   Proanthocyanins       178 non-null    float64
 9   Color_Intensity       178 non-null    float64
 10  Hue                   178 non-null    float64
 11  OD280                 178 non-null    float64
 12  Proline               178 non-null    int64  
dtypes: float64(11), int64(2)
memory usage: 18.2 KB

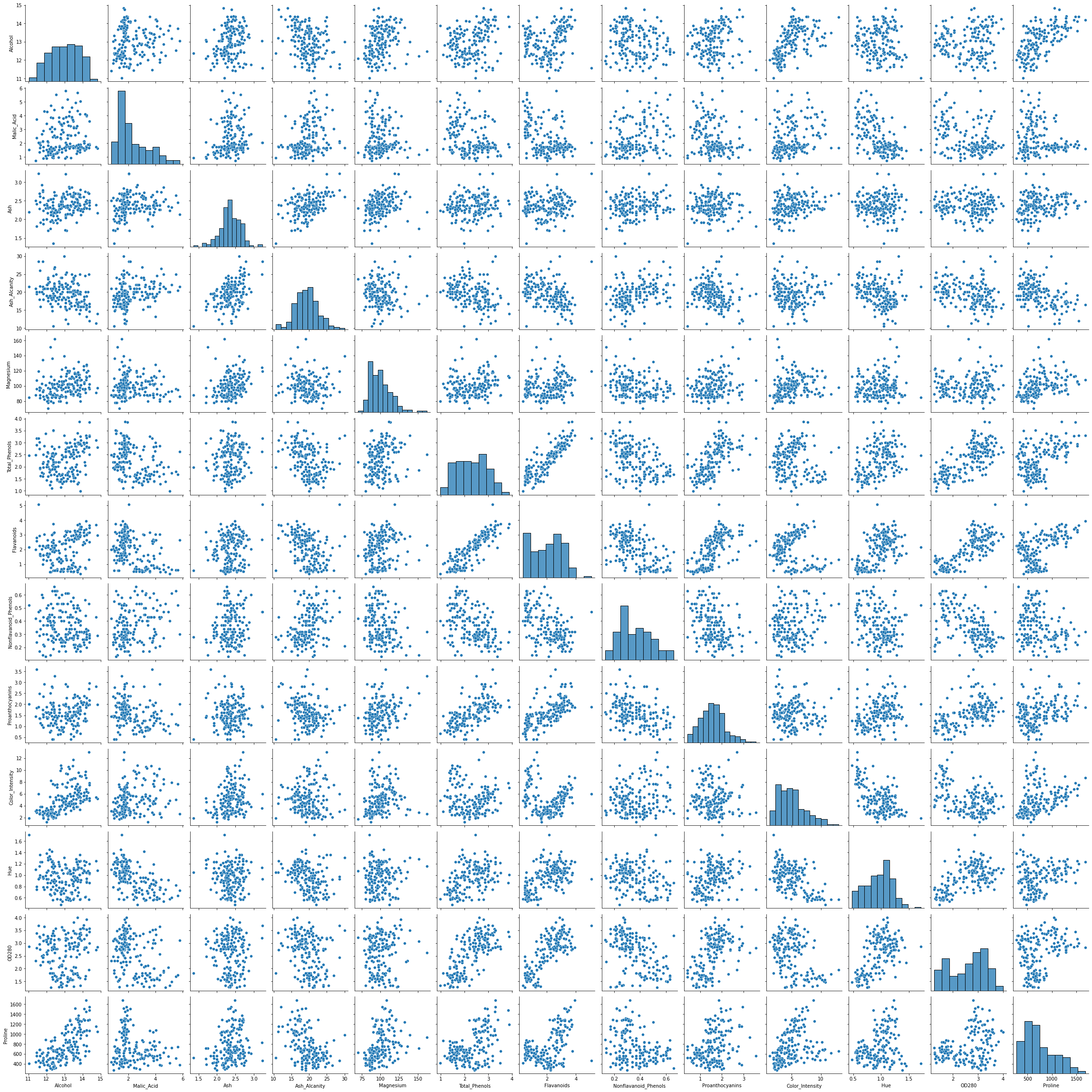
Nincs szükség adatok eldobására vagy bevitelére, mivel az adatkészletben nincsenek üres értékek. Használhatunk Seabornt pairplot() az adatok eloszlásának megtekintéséhez és annak ellenőrzéséhez, hogy az adatkészlet olyan oszloppárokat alkot-e, amelyek érdekesek lehetnek a fürtözéshez:

sns.pairplot(df)

Ha a párrajzot nézzük, két oszlop tűnik ígéretesnek a klaszterezés szempontjából – Alcohol és a OD280 (amely a borok fehérjekoncentrációjának meghatározására szolgáló módszer). Úgy tűnik, hogy 3 különböző klaszter van a telkeken, amelyek kettőt egyesítenek.

Vannak más oszlopok is, amelyek úgy tűnik, hogy összefüggésben vannak. Leginkább Alcohol és a Total_Phenolsés Alcohol és a Flavanoids. Nagyszerű lineáris kapcsolataik vannak, amelyek a párdiagramon megfigyelhetők.

Mivel a hangsúly a K-Means-szel való klaszterezésen van, válasszunk mondjuk egy oszloppárt Alcohol és a OD280, és tesztelje a könyök módszert ehhez az adatkészlethez.

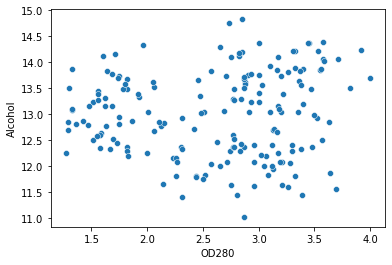
Ábrázoljuk a szórást úgy, hogy a két oszlop legyen a tengelye, hogy közelebbről is megnézhessük azokat a pontokat, amelyeket csoportokra szeretnénk osztani:

sns.scatterplot(data=df, x='OD280', y='Alcohol')

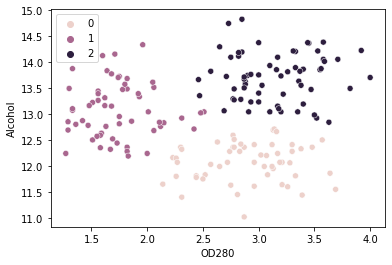
Most már meghatározhatjuk oszlopainkat, és a könyök módszerrel határozhatjuk meg a klaszterek számát. Ezzel is elindítjuk az algoritmust kmeans++ csak azért, hogy gyorsabban konvergáljon:

values = df[['OD280', 'Alcohol']]

wcss_wine = [] 
for i in range(1, 11): 
    kmeans = KMeans(n_clusters = i, init = 'k-means++', random_state = 42)
    kmeans.fit(values) 
    wcss_wine.append(kmeans.inertia_)

Kiszámoltuk a WCSS-t, így ábrázolhatjuk az eredményeket:

clusters_wine = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
plt.plot(clusters_wine, wcss_wine)
plt.axvline(3, linestyle='--', color='r')

A könyök módszer szerint itt 3 klaszternek kell lennie. Az utolsó lépésben gyűjtsük össze pontjainkat 3 klaszterbe, és ábrázoljuk a színekkel azonosított klasztereket:

kmeans_wine = KMeans(n_clusters=3, random_state=42)
kmeans_wine.fit(values)
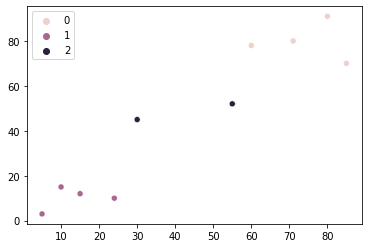
sns.scatterplot(x = values['OD280'], y = values['Alcohol'], hue=kmeans_wine.labels_)

Klasztereket láthatunk 0, 1és 2 a grafikonon. Elemzésünk alapján 0 csoport magasabb fehérjetartalmú és alacsonyabb alkoholtartalmú borokat tartalmaz, 1 csoport magasabb alkoholtartalmú és alacsony fehérjetartalmú borai vannak, ill 2 csoport boraiban magas a fehérje és az alkohol is.

Ez egy nagyon érdekes adatkészlet, és arra biztatlak, hogy menjen tovább az elemzésbe az adatok normalizálás és PCA utáni klaszterezésével – az eredmények értelmezésével és új kapcsolatok keresésével is.

Következtetés

K-Means A klaszterezés egy egyszerű, de nagyon hatékony, felügyelt gépi tanulási algoritmus az adatfürtözéshez. Az adatokat az adatpontok közötti euklideszi távolság alapján csoportosítja. A K-Means fürtözési algoritmus számos felhasználási lehetőséget kínál szöveges dokumentumok, képek, videók és sok más csoportosítására.