Végleges útmutató a logisztikai regresszióhoz Pythonban

Bevezetés

Néha összetévesztik lineáris regresszió kezdők által – a kifejezés megosztása miatt regresszió - logisztikus regresszió messze eltér attól lineáris regresszió. Míg a lineáris regresszió előrejelzi az olyan értékeket, mint a 2, 2.45, 6.77 vagy folytonos értékek, így a regresszió algoritmus, logisztikus regresszió előrejelzi a 0 vagy 1, 1 vagy 2 vagy 3 értékeket, amelyek azok diszkrét értékek, így a besorolás algoritmus. Igen, úgy hívják regresszió hanem a besorolás algoritmus. Bővebben erről egy pillanat alatt.

Ezért, ha adattudományi problémája folytonos értékeket foglal magában, alkalmazhatja a regresszió algoritmus (a lineáris regresszió az egyik ilyen). Ellenkező esetben, ha bemenetek, diszkrét értékek vagy osztályok osztályozásáról van szó, alkalmazhatja a besorolás algoritmus (a logisztikus regresszió az egyik ilyen).

Ebben az útmutatóban logisztikus regressziót hajtunk végre Pythonban a Scikit-Learn könyvtárral. Azt is elmagyarázzuk, hogy miért ez a szó "regresszió" jelen van a névben, és hogyan működik a logisztikus regresszió.

Ehhez először olyan adatokat töltünk be, amelyeket besorolunk, megjelenítünk és előfeldolgozunk. Ezután felállítunk egy logisztikus regressziós modellt, amely megérti ezeket az adatokat. Ezt a modellt ezután kiértékelik, és az új bemenet alapján értékek előrejelzésére használják.

Motiváció

A cég, amelynek dolgozik, partnerséget kötött egy török ​​mezőgazdasági gazdasággal. Ez a partnerség tökmagok értékesítését foglalja magában. A tökmag nagyon fontos az emberi táplálkozás szempontjából. Jó arányban tartalmaznak szénhidrátot, zsírt, fehérjét, kalciumot, káliumot, foszfort, magnéziumot, vasat és cinket.

Az adattudományi csapatban az a feladatod, hogy pusztán adatok felhasználásával különbséget tudj tenni a tökmag fajtái között – ill. osztályozó az adatokat vetőmag típus szerint.

A török ​​gazdaság kétféle tökmaggal dolgozik, az egyik ún Çerçevelik és a másik Ürgüp Sivrisi.

A tökmagok besorolásához csapata a 2021-es papírt követte „A gépi tanulási módszerek alkalmazása a tökmag (Cucurbita pepo L.) osztályozásában. Genetikai erőforrások és termésfejlődés” Koklutól, Sarigiltől és Ozbektől – ebben a cikkben van egy módszertan a magméretek fényképezésére és a képekből való kinyerésére.

A cikkben leírt folyamat befejezése után a következő méréseket vontuk ki:

• Terület – a pixelek száma a tökmag határain belül
• kerülete – a tökmag kerülete pixelben
• Főtengely hossza – a tökmag kerületét is pixelben
• Kis tengelyhossz – a tökmag kis tengelytávolsága
• Különcség – a tökmag különcsége
• Konvex terület – a legkisebb konvex héj képpontjainak száma a tökmag által alkotott területen
• terjedelme – a tökmag területének aránya a határoló doboz képpontjaihoz viszonyítva
• Egyenértékű átmérő – a tökmag területének néggyel való szorzatának négyzetgyöke osztva pi-vel
• tömörség – a tökmag területének aránya az azonos kerületű kör területéhez viszonyítva
• szilárdság – a tökmag domború és domború állapota
• Kerekség – a tökmag oválissága anélkül, hogy figyelembe vennénk a szélek torzulásait
• Aspect Ratio – a tökmag oldalaránya

Ezekkel a mérésekkel kell dolgozni. A mérések mellett ott van még a Osztály címke a kétféle tökmaghoz.

A magok osztályozásának megkezdéséhez importáljuk az adatokat, és kezdjük el megnézni azokat.

Az adatkészlet megértése

Az adatkészlet letöltése után a segítségével betölthetjük egy adatkeret-struktúrába pandas könyvtár. Mivel ez egy excel fájl, a read_excel() eljárás:

import pandas as pd

fpath = 'dataset/pumpkin_seeds_dataset.xlsx' 
df = pd.read_excel(fpath)

Az adatok betöltése után gyorsan megtekinthetjük az első 5 sort a segítségével head() eljárás:

df.head() 

Ennek eredményeként:

	Area 	Perimeter 	Major_Axis_Length 	Minor_Axis_Length 	Convex_Area 	Equiv_Diameter 	Eccentricity 	Solidity 	Extent 	Roundness 	Aspect_Ration 	Compactness 	Class
0 	56276 	888.242 	326.1485 			220.2388 			56831 			267.6805 		0.7376 			0.9902 		0.7453 	0.8963 		1.4809 			0.8207 			Çerçevelik
1 	76631 	1068.146 	417.1932 			234.2289 			77280 			312.3614 		0.8275 			0.9916 		0.7151 	0.8440 		1.7811 			0.7487 			Çerçevelik
2 	71623 	1082.987 	435.8328 			211.0457 			72663 			301.9822 		0.8749 			0.9857 		0.7400 	0.7674 		2.0651 			0.6929 			Çerçevelik
3 	66458 	992.051 	381.5638 			222.5322 			67118 			290.8899 		0.8123 			0.9902 		0.7396 	0.8486 		1.7146 			0.7624 			Çerçevelik
4 	66107 	998.146 	383.8883 			220.4545 			67117 			290.1207 		0.8187 			0.9850 		0.6752 	0.8338 		1.7413 			0.7557 			Çerçevelik

Itt minden mérés megtalálható a megfelelő oszlopokban, a miénkben jellemzők, valamint a Osztály rovat, a mi cél, amely az utolsó az adatkeretben. A segítségével láthatjuk, hogy hány mérésünk van shape tulajdonság:

df.shape 

A kimenet:

(2500, 13)

Az alakzat eredménye azt mutatja, hogy 2500 bejegyzés (vagy sor) van az adatkészletben és 13 oszlopban. Mivel tudjuk, hogy egy céloszlop van, ez azt jelenti, hogy 12 jellemzőoszlopunk van.

Most felfedezhetjük a célváltozót, a tökmagot Class. Mivel ezt a változót megjósoljuk, érdekes látni, hogy az egyes tökmagokból hány mintánk van. Általában minél kisebb a különbség az osztályainkban előforduló példányok száma között, annál kiegyensúlyozottabb a mintánk, és annál jobbak az előrejelzéseink.

Ezt az ellenőrzést úgy végezhetjük el, hogy minden vetőmagmintát megszámlálunk a value_counts() eljárás:

df['Class'].value_counts() 

A fenti kód a következőt jeleníti meg:

Çerçevelik       1300
Ürgüp Sivrisi    1200
Name: Class, dtype: int64

Láthatjuk, hogy 1300 minta van a Çerçevelik vetőmag és 1200 minta a Ürgüp Sivrisi mag. Figyeljük meg, hogy a különbség közöttük 100 minta van, ez egy nagyon kicsi különbség, ami jó nekünk, és azt jelzi, hogy nincs szükség a minták számának újraegyensúlyozására.

Nézzük meg a szolgáltatásaink leíró statisztikáit is a describe() módszerrel, hogy megtudja, mennyire jól oszlanak el az adatok. Az eredményül kapott táblázatot is transzponáljuk -val T a statisztikák összehasonlításának megkönnyítése érdekében:

df.describe().T

A kapott táblázat a következő:

					count 	mean 			std 			min 		25% 			50% 			75% 			max
Area 				2500.0 	80658.220800 	13664.510228 	47939.0000 	70765.000000 	79076.00000 	89757.500000 	136574.0000
Perimeter 			2500.0 	1130.279015 	109.256418 		868.4850 	1048.829750 	1123.67200 		1203.340500 	1559.4500
Major_Axis_Length 	2500.0 	456.601840 		56.235704 		320.8446 	414.957850 		449.49660 		492.737650 		661.9113
Minor_Axis_Length 	2500.0 	225.794921 		23.297245 		152.1718 	211.245925 		224.70310 		240.672875 		305.8180
Convex_Area 		2500.0 	81508.084400 	13764.092788 	48366.0000 	71512.000000 	79872.00000 	90797.750000 	138384.0000
Equiv_Diameter 		2500.0 	319.334230 		26.891920 		247.0584 	300.167975 		317.30535 		338.057375 		417.0029
Eccentricity 		2500.0 	0.860879 		0.045167 		0.4921 		0.831700 		0.86370 		0.897025 		0.9481
Solidity 			2500.0 	0.989492 		0.003494 		0.9186 		0.988300 		0.99030 		0.991500 		0.9944
Extent 				2500.0 	0.693205 		0.060914 		0.4680 		0.658900 		0.71305 		0.740225 		0.8296
Roundness 			2500.0 	0.791533 		0.055924 		0.5546 		0.751900 		0.79775 		0.834325 		0.9396
Aspect_Ration 		2500.0 	2.041702 		0.315997 		1.1487 		1.801050 		1.98420 		2.262075 		3.1444
Compactness 		2500.0 	0.704121 		0.053067 		0.5608 		0.663475 		0.70770 		0.743500 		0.9049

A táblázatot nézve, ha összehasonlítjuk a jelent és a szórás (std) oszlopokban látható, hogy a legtöbb jellemző átlaga messze van a szórástól. Ez azt jelzi, hogy az adatértékek nem az átlagérték köré koncentrálódnak, hanem jobban szétszórva vannak körülötte – más szóval, nagy változékonyság.

Továbbá, ha megnézzük a minimum (min) És maximális (max) oszlopok, egyes funkciók, mint pl Areaés Convex_Area, nagy különbségek vannak a minimális és maximális értékek között. Ez azt jelenti, hogy ezekben az oszlopokban nagyon kis adatok és nagyon nagyok az adatok, ill nagyobb amplitúdójú adatértékek között.

A nagy változékonyság, nagy amplitúdó és a különböző mértékegységekkel rendelkező jellemzők miatt a legtöbb adatunknak előnyös lenne, ha minden jellemzőre ugyanaz a skála lenne, vagy pikkelyes. Az adatskálázás az adatokat az átlag köré összpontosítja, és csökkenti a szórását.

Ez a forgatókönyv valószínűleg azt is jelzi, hogy az adatokban vannak kiugró értékek és szélsőséges értékek. Tehát a legjobb, ha van néhány kiugró kezelés az adatok skálázása mellett.

Vannak gépi tanulási algoritmusok, például fa alapú algoritmusok, mint pl Véletlenszerű erdőbesorolás, amelyeket nem érintenek a nagy adatvarianciák, a kiugró értékek és a szélsőséges értékek. Logisztikus regresszió eltérő, egy olyan függvényen alapul, amely kategorizálja az értékeinket, és ennek a függvénynek a paramétereit befolyásolhatják az általános adattrenden kívül eső, nagy szórással rendelkező értékek.

A logisztikai regresszióról egy kicsit többet fogunk tudni, amikor végre fogjuk hajtani. Egyelőre tovább kutathatjuk adatainkat.

Az adatok megjelenítése

Mostanáig a leíró statisztikákkal némileg absztrakt pillanatképet kaptunk az adatok bizonyos tulajdonságairól. Egy másik fontos lépés, hogy vizualizáljuk, és megerősítsük a nagy variancia, amplitúdó és kiugró értékekre vonatkozó hipotézisünket. Ahhoz, hogy megnézzük, az eddig megfigyeltek megjelennek-e az adatokban, néhány grafikont ábrázolhatunk.

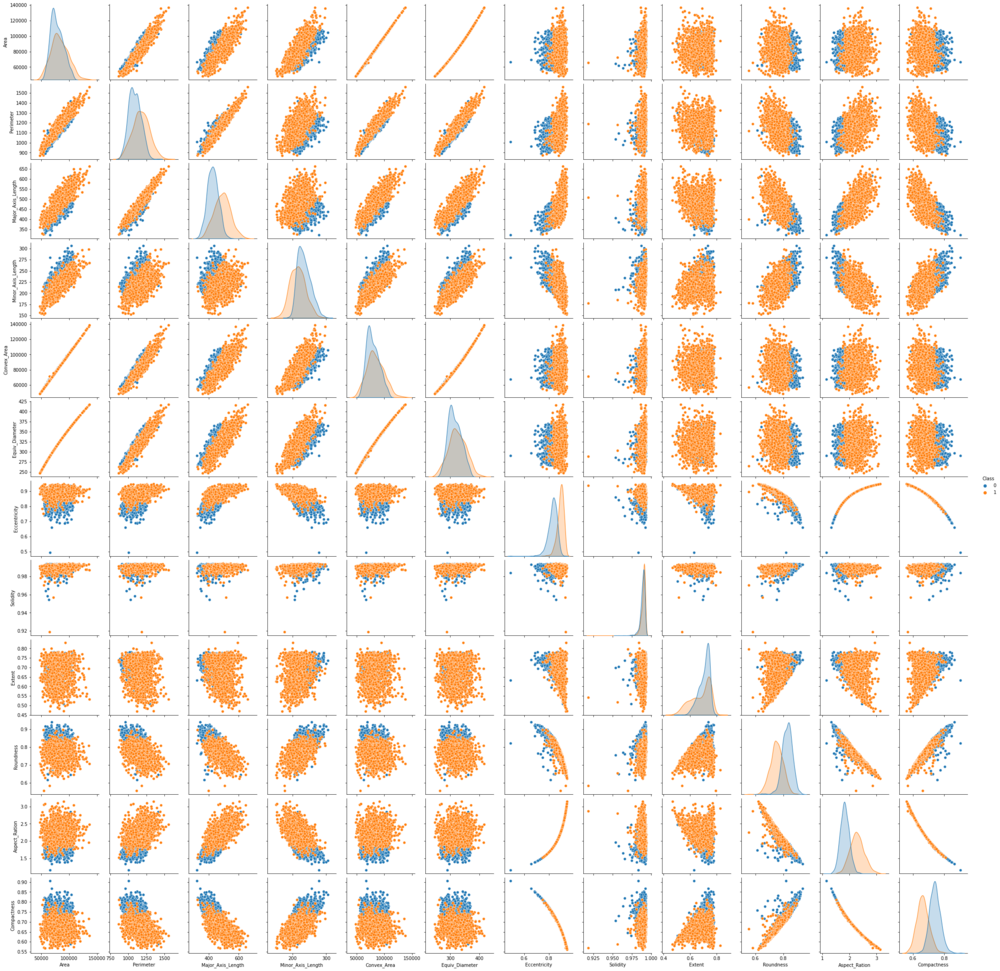
Az is érdekes látni, hogy a jellemzők hogyan kapcsolódnak a két előrejelzett osztályhoz. Ehhez importáljuk a seaborn csomagolja be és használja a pairplot grafikonon az egyes jellemzők eloszlását és az egyes jellemzőnkénti osztályok szétválasztását tekintheti meg:

import seaborn as sns


sns.pairplot(data=df, hue='Class')

A párrajzot nézve láthatjuk, hogy a legtöbb esetben a pontok a Çerçevelik osztály egyértelműen elkülönül a pontjaitól Ürgüp Sivrisi osztály. Vagy az egyik osztály pontjai jobbra vannak, amikor a többiek balra, vagy egyesek fent, míg a többiek lent. Ha valamilyen görbét vagy vonalat használnánk az osztályok elválasztására, akkor ez azt mutatja, hogy könnyebben lehet szétválasztani őket, ha keverve lenne, akkor az osztályozás nehezebb feladat lenne.

A Eccentricity, Compactness és a Aspect_Ration oszlopok között néhány „elszigetelt”, vagy az általános adattrendtől eltérő pont – kiugró – is könnyen észrevehető.

Ha az átlót a diagram bal felső sarkától jobb alsó felé nézzük, figyeljük meg, hogy az adatok eloszlása ​​is színkódolt osztályaink szerint. Az eloszlási alakzatok és a két görbe közötti távolság másik mutatója annak, hogy mennyire elválaszthatók – minél távolabb vannak egymástól, annál jobb. A legtöbb esetben nincsenek egymásra rakva, ami azt jelenti, hogy könnyebben szétválaszthatók, ezzel is hozzájárulva a mi feladatunkhoz.

Sorozatban az összes változó boxplotját is ábrázolhatjuk a sns.boxplot() módszer. Legtöbbször hasznos a boxplotok vízszintes tájolása, így a boxplotok alakjai megegyeznek az eloszlási alakzatokkal, ezt megtehetjük a orient érv:

sns.boxplot(data=df, orient='h') 

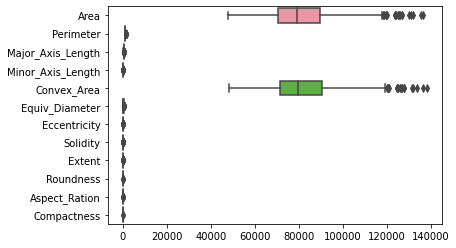
A fenti cselekményben ezt vegyük észre Area és a Convex_Area olyan nagy magnitúdójuk van a többi oszlophoz képest, hogy összenyomják a többi boxplotot. Ahhoz, hogy az összes boxplotot megnézhessük, méretezhetjük a jellemzőket, és újra ábrázolhatjuk őket.

Mielőtt ezt megtennénk, értsük meg, hogy ha vannak olyan jellemzők értékei, amelyek szoros kapcsolatban állnak más értékekkel, például ha vannak olyan értékek, amelyek szintén nagyobbak lesznek, amikor más jellemzők értékei nőnek, pozitív korreláció; vagy ha vannak olyan értékek, amelyek az ellenkezőjét csinálják, akkor kisebbek lesznek, míg más értékek kisebbek lesznek, és a Negatív korreláció.

Ezt azért fontos megnézni, mert az adatok erős kapcsolatai azt jelenthetik, hogy egyes oszlopok más oszlopokból származnak, vagy a mi modellünkhöz hasonló jelentéssel bírnak. Ha ez megtörténik, előfordulhat, hogy a modell eredményeit túlbecsülik, és olyan eredményeket szeretnénk elérni, amelyek közelebb állnak a valósághoz. Ha erős korrelációk vannak, az azt is jelenti, hogy csökkenthetjük a funkciók számát, és kevesebb oszlopot használhatunk, így a modell még jobb. takarékos.

Vessünk egy pillantást a változók közötti összefüggésekre, majd áttérhetünk az adatok előfeldolgozására. Kiszámoljuk az összefüggéseket a corr() módszerrel, és vizualizálja őket Seaborn's segítségével heatmap(). A hőtérkép szabványos mérete általában kicsi, ezért importálni fogjuk matplotlib (általános vizualizációs motor/könyvtár, amelyre a Seaborn épül), és módosítsa a méretet figsize:

import matplotlib.pyplot as plt
plt.figure(figsize=(15, 10))

correlations = df.corr()
sns.heatmap(correlations, annot=True) 

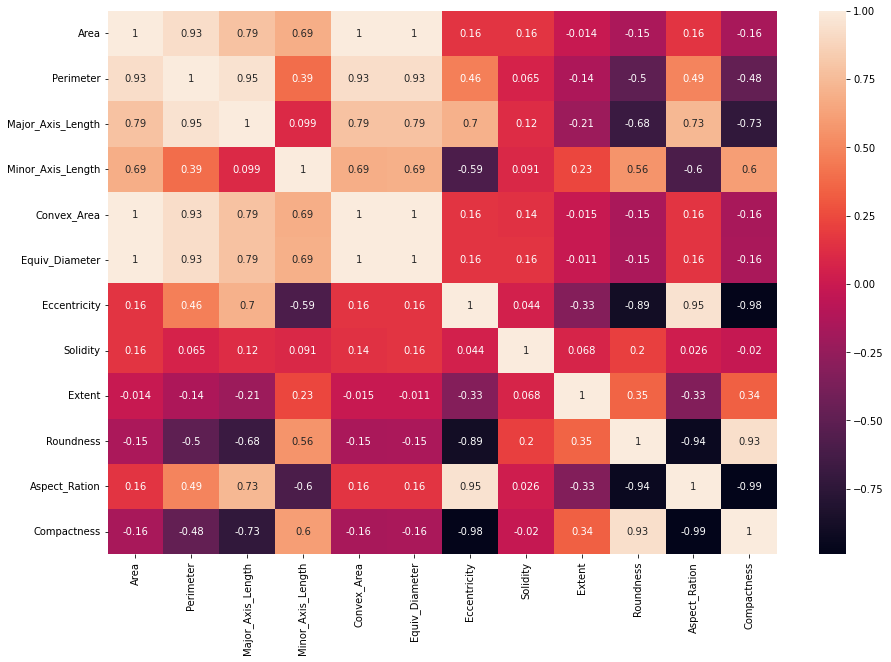
Ebben a hőtérképben az 1-hez vagy -1-hez közelebbi értékek azok az értékek, amelyekre figyelnünk kell. Az első eset magas pozitív korrelációt jelöl, a második pedig magas negatív korrelációt. Mindkét érték, ha nem magasabb, mint 0.8 vagy -0.8, előnyös lesz logisztikus regressziós modellünk számára.

Amikor magas korrelációk vannak, mint például az 0.99 között Aspec_Ration és a Compactness, ez azt jelenti, hogy csak a használatát választhatjuk Aspec_Ration vagy csak Compactness, mindkettő helyett (mivel majdnem egyenlőek lennének prediktorok egymástól). Ugyanez vonatkozik rá Eccentricity és a Compactness val,-vel -0.98 korreláció, for Area és a Perimeter val,-vel 0.94 korreláció és néhány más oszlop.

Az adatok előfeldolgozása

Mivel az adatokat már egy ideje feltártuk, megkezdhetjük az előfeldolgozást. Egyelőre használjuk az összes szolgáltatást az osztály előrejelzéséhez. Miután megkaptuk az első modellt, az alapvonalat, eltávolíthatunk néhány erősen korrelált oszlopot, és összehasonlíthatjuk az alapvonallal.

A jellemző oszlopok a miénk lesznek X adatok és az osztályoszlop, a mi y céladatok:

y = df['Class']
X = df.drop(columns=['Class'], axis=1)

Kategorikus jellemzők numerikus jellemzőkké alakítása

A miénkkel kapcsolatban Class oszlop – értékei nem számok, ez azt jelenti, hogy transzformálni is kell őket. Számos módja van ennek az átalakításnak; itt fogjuk használni a replace() módszert és cserélje ki Çerçevelik nak nek 0 és a Ürgüp Sivrisi nak nek 1.

y = y.replace('Çerçevelik', 0).replace('Ürgüp Sivrisi', 1)

Tartsa szem előtt a térképezést! A modell eredményeinek olvasásakor legalább gondolatban vissza kell konvertálnia ezeket, vagy más felhasználók osztálynevére.

Az adatok felosztása vonat- és tesztkészletekre

Feltárásunk során észrevettük, hogy a funkciók méretezésre szorulnak. Ha most, vagy automatikusan elvégeznénk a skálázást, akkor az értékeket a teljes egészével skáláznánk X és a y. Ebben az esetben bemutatnánk adatszivárgás, mivel a hamarosan megjelenő tesztkészlet értékei befolyásolták volna a skálázást. Az adatszivárgás gyakori oka az ML modellek reprodukálhatatlan eredményeinek és illuzórikusan nagy teljesítményének.

A skálázáson való gondolkodás azt mutatja, hogy először fel kell osztanunk X és a y az adatokat tovább a vonat- és tesztkészletekbe, majd a megfelelő egy skálázót az edzőkészleten, és a át mind a vonat, mind a tesztkészlet (anélkül, hogy a tesztkészlet valaha is hatással lenne az ezt végző skálázóra). Ehhez a Scikit-Learn-t fogjuk használni train_test_split() eljárás:

from sklearn.model_selection import train_test_split
SEED = 42 

X_train, X_test, y_train, y_test = train_test_split(X, y, 
                                                    test_size=.25, 
                                                    random_state=SEED)

Beállítás test_size=.25 biztosítja, hogy az adatok 25%-át tesztelésre, 75%-át pedig képzésre használjuk fel. Ez elhagyható, ha ez az alapértelmezett felosztás, de a Pythonic A kódírás módja azt tanácsolja, hogy „jobb explicitnek lenni, mint implicitnek”.

Miután felosztotta az adatokat vonat- és tesztkészletekre, célszerű megnézni, hány rekord van az egyes halmazokban. Ezt meg lehet tenni a shape tulajdonság:

X_train.shape, X_test.shape, y_train.shape, y_test.shape

Ez a következőket jeleníti meg:

((1875, 12), (625, 12), (1875,), (625,))

Láthatjuk, hogy a felosztás után 1875 edzésre és 625 tesztelésre vonatkozó rekordunk van.

Adatok skálázása

Ha elkészültünk a vonat- és tesztkészleteinkkel, folytathatjuk az adatok skálázását a Scikit-Learn segítségével StandardScaler objektum (vagy más, a könyvtár által biztosított skálázó). A szivárgás elkerülése érdekében a vízkőoldót a X_train az adatokat és a vonatértékeket ezután a vonat és a vizsgálati adatok skálázására vagy átalakítására használják:

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

Mivel általában hívja:

scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)

Az első két sor egyes számmal összecsukható fit_transform() hívást, amely a készüléken lévő skálázóhoz illeszkedik, és egy mozdulattal átalakítja azt. Most már reprodukálhatjuk a boxplot grafikonokat, hogy lássuk a különbséget az adatok skálázása után.

Tekintettel arra, hogy a méretezés eltávolítja az oszlopneveket, az ábrázolás előtt a vonatadatokat ismét egy adatkeretbe rendezhetjük oszlopnevekkel, hogy megkönnyítsük a megjelenítést:

column_names = df.columns[:12] 
X_train = pd.DataFrame(X_train, columns=column_names)

sns.boxplot(data=X_train, orient='h')

Végre láthatjuk az összes boxplotunkat! Figyeljük meg, hogy mindegyiknek vannak kiugró értékei, és olyan jellemzők, amelyek a normáltól távolabbi eloszlást mutatnak (amelyek görbéi balra vagy jobbra ferdülnek), mint pl. Solidity, Extent, Aspect_Rationés Compactedness, ugyanazok, amelyek magasabb korrelációt mutattak.

Kiugró értékek eltávolítása IQR módszerrel

Azt már tudjuk, hogy a logisztikai regressziót kiugró értékek is befolyásolhatják. A kezelésük egyik módja az ún Interquartilis tartomány or I.Q.R.. Az IQR módszer kezdeti lépése a vonatadatok négy részre, úgynevezett kvartilisre osztása. Az első kvartilis, Q1, az adatok 25%-át teszi ki, a második, Q2, 50%-ra, a harmadik, Q375%-ra, és az utolsó, Q4, 100%-ra. A boxplot dobozai az IQR módszerrel vannak meghatározva, és annak vizuális megjelenítése.

Vízszintes boxplot esetén a bal oldali függőleges vonal az adatok 25%-át, a középső függőleges vonal az adatok (vagy medián) 50%-át, a jobb oldali utolsó függőleges vonal az adatok 75%-át jelöli. . Minél egyenletesebb méretű mindkét függőleges vonallal meghatározott négyzet – vagy minél inkább középen van a középső függőleges vonal –, az azt jelenti, hogy adataink közelebb állnak a normál eloszláshoz, vagy kevésbé torzulnak, ami hasznos az elemzésünkben.

Az IQR dobozon kívül vízszintes vonalak is találhatók mindkét oldalán. Ezek a vonalak jelölik az által meghatározott minimális és maximális eloszlási értékeket

$$
Minimum = Q1 – 1.5*IQR
$$

és a

$$
Maximum = Q3 + 1.5*IQR
$$

Az IQR pontosan a Q3 és Q1 (vagy Q3 – Q1) közötti különbség, és ez az adatok legközpontibb pontja. Éppen ezért az IQR megkeresésekor a kiugró értékeket az adatszélsőségekben, illetve a minimum és maximum pontokban szűrjük ki. A dobozos ábrák bepillantást engednek abba, hogy mi lesz az IQR módszer eredménye.

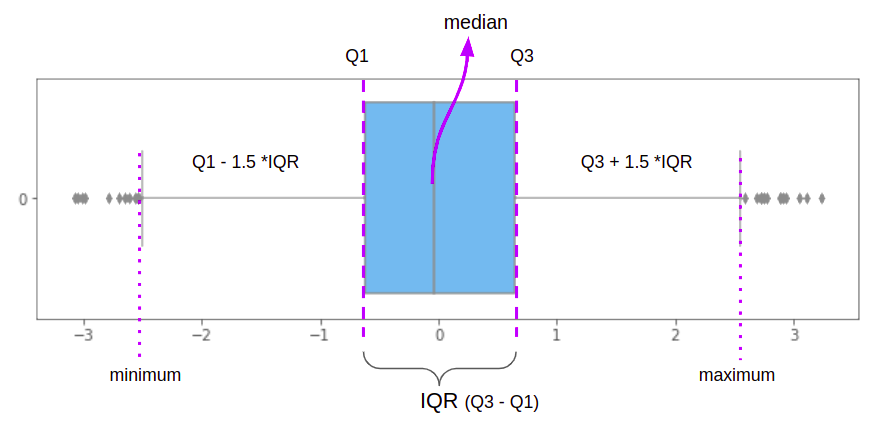
Használhatjuk a Pandákat quantile() módszer a kvantiliseink megtalálására, és iqr tól scipy.stats csomag az egyes oszlopok interkvartilis adattartományának beszerzéséhez:

from scipy.stats import iqr

Q1 = X_train.quantile(q=.25)
Q3 = X_train.quantile(q=.75)

IQR = X_train.apply(iqr)

Most van Q1, Q3 és IQR, kiszűrhetjük a mediánhoz közelebbi értékeket:

minimum = X_train < (Q1-1.5*IQR)
maximum = X_train > (Q3+1.5*IQR)


filter = ~(minimum | maximum).any(axis=1)


X_train = X_train[filter]

A képzési soraink szűrése után láthatjuk, hogy hány darab van még az adatokban shape:

X_train.shape

Ennek eredményeként:

(1714, 12)

Láthatjuk, hogy a sorok száma szűrés után 1875-ről 1714-re változott. Ez azt jelenti, hogy 161 sor tartalmazott kiugró értékeket, vagyis az adatok 8.5%-a.

A kiugró értékek eltávolítása után már majdnem készen állunk az adatok felvételére a modellbe. A modellillesztéshez vonatadatokat fogunk használni. X_train ki van szűrve, de mi van y_train?

y_train.shape

Ez a következő kimenetet adja:

(1875,)

Figyelj erre y_train még mindig 1875 sora van. Egyeztetni kell a számát y_train sorok számához X_train sorokat és nem csak önkényesen. El kell távolítanunk az általunk eltávolított tökmag példányok y-értékeit, amelyek valószínűleg szétszóródtak a y_train készlet. A szűrt X_train stil-nek megvannak az eredeti indexei, és az indexben vannak rések, ahol eltávolítottuk a kiugró értékeket! Ezután használhatjuk az indexet X_train DataFrame a megfelelő értékek kereséséhez y_train:

y_train = y_train.iloc[X_train.index]

Ezt követően megtekinthetjük a y_train alak újra:

y_train.shape

Melyik kimenet:

(1714,)

Most, y_train szintén 1714 sorral rendelkezik, és megegyeznek a X_train sorokat. Végre készen állunk logisztikus regressziós modellünk megalkotására!

A logisztikai regressziós modell megvalósítása

A nehéz rész kész! Az előfeldolgozás általában nehezebb, mint a modellfejlesztés, ha olyan könyvtárak használatáról van szó, mint a Scikit-Learn, amelyek az ML modellek alkalmazását csak néhány sorra egyszerűsítették.

Először is importáljuk a LogisticRegression osztályt és példányosítani, létrehozva a LogisticRegression tárgy:

from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression(random_state=SEED)

Másodszor, a vonatadatokat a logreg modell a fit() módszerrel, és megjósoljuk tesztadatainkat a predict() módszerrel, az eredményeket mint y_pred:

logreg.fit(X_train.values, y_train)
y_pred = logreg.predict(X_test)

Modellünkkel már jóslatokat tettünk! Nézzük az első 3 sort X_train hogy megnézzük, milyen adatokat használtunk fel:

X_train[:3]

A fenti kód kimenete:

       Area          Perimeter     Major_Axis_Length    Minor_Axis_Length    Convex_Area   Equiv_Diameter       Eccentricity  Solidity      Extent        Roundness     Aspect_Ration        Compactness
0      -1.098308     -0.936518     -0.607941            -1.132551            -1.082768     -1.122359            0.458911      -1.078259     0.562847      -0.176041     0.236617             -0.360134
1      -0.501526     -0.468936     -0.387303            -0.376176            -0.507652     -0.475015            0.125764      0.258195      0.211703      0.094213      -0.122270            0.019480
2      0.012372      -0.209168     -0.354107            0.465095              0.003871      0.054384            -0.453911     0.432515      0.794735      0.647084      -0.617427            0.571137

És az első 3 jóslatnál be y_pred az eredmények megtekintéséhez:

y_pred[:3] 

Ennek eredményeként:

array([0, 0, 0])

Erre a három sorra azt jósoltuk, hogy az első osztályú magok, Çerçevelik.

A logisztikus regresszió, a végső osztály előrejelzése helyett, mint pl 0, azt is megjósolhatjuk, hogy a sor mekkora valószínűséggel tartozik a 0 osztály. Valójában ez történik, amikor a logisztikus regresszió osztályozza az adatokat, és a predict() metódus ezután átadja ezt az előrejelzést egy küszöbértéken, hogy visszaadja a „kemény” osztályt. Az osztályhoz való kapcsolódás valószínűségének előrejelzéséhez, predict_proba() használt:

y_pred_proba = logreg.predict_proba(X_test)

Nézzük meg az y valószínűségi előrejelzések első 3 értékét is:

y_pred_proba[:3] 

Melyik kimenet:

        # class 0   class 1   
array([[0.54726628, 0.45273372],
       [0.56324527, 0.43675473],
       [0.86233349, 0.13766651]])

Most három nulla helyett minden osztályhoz egy oszlop tartozik. A bal oldali oszlopban, kezdve a 0.54726628, az osztályra vonatkozó adatok valószínűségei 0; és a jobb oldali oszlopban a következővel kezdve 0.45273372, annak a valószínűsége, hogy az osztályra vonatkozik 1.

További információ található arról, hogyan készült a várható kimenet. Valójában nem volt 0, de 55% az esély az osztályra 0, és 45% esélye van az osztálynak 1. Így látszik az első három X_test osztályra vonatkozó adatpontok 0, csak a harmadik adatpont tekintetében igazán egyértelműek, 86%-os valószínűséggel – és nem annyira az első két adatpont esetében.

Amikor az eredményeket ML módszerekkel közöljük – általában a legjobb, ha egy soft osztályt ad vissza, és a kapcsolódó valószínűséget "bizalom" annak a besorolásnak.

Ennek kiszámításáról bővebben fogunk beszélni, ha mélyebben belemegyünk a modellbe. Ebben az időben továbbléphetünk a következő lépésre.

A modell értékelése osztályozási jelentésekkel

A harmadik lépés annak megtekintése, hogy a modell hogyan teljesít a tesztadatokon. Importálhatjuk a Scikit-Learn-t classification_report() és adja át a miénket y_test és a y_pred mint érvek. Ezt követően kinyomtathatjuk a válaszát.

Az osztályozási jelentés tartalmazza a leggyakrabban használt osztályozási mérőszámokat, mint pl pontosság, visszahívás, f1-pontszámés pontosság.

1. Pontosság: hogy megértsük, milyen helyes előrejelzési értékeket tartott helyesnek osztályozónk. A pontosság elosztja ezeket a valódi pozitív értékeket bármivel, amit pozitívnak jósoltak:

$$
pontosság = töredék{szöveg{igaz pozitív}}{szöveg{igaz pozitív} + szöveg{hamis pozitív}}
$$

2. visszahívás: hogy megértsük, hány valódi pozitívumot azonosított az osztályozónk. A visszahívás kiszámítása úgy történik, hogy a valódi pozitívumot elosztjuk bármivel, amit pozitívnak kellett volna előre jelezni:

$$
visszahívás = töredék{szöveg{igaz pozitív}}{szöveg{igaz pozitív} + szöveg{hamis negatív}}
$$

3. F1 pontszám: a kiegyensúlyozott ill harmonikus átlag pontosság és felidézés. A legalacsonyabb érték 0, a legmagasabb pedig 1. Amikor f1-score egyenlő 1-gyel, ez azt jelenti, hogy minden osztályt helyesen jósoltak meg – ezt a pontszámot nagyon nehéz megszerezni valós adatokkal:

$$
text{f1-score} = 2* frac{text{precision} * text{recall}}{text{precision} + text{recall}}
$$

4. Pontosság: azt írja le, hogy az osztályozónk hány jóslatot kapott. A legalacsonyabb pontossági érték 0, a legmagasabb pedig 1. Ezt az értéket általában megszorozzák 100-zal, hogy megkapják a százalékot:

$$
pontosság = frac{szöveg{helyes előrejelzések száma}}{szöveg{jóslatok teljes száma}}
$$

from sklearn.metrics import classification_report
cr = classification_report(y_test, y_pred)
print(cr)

Ezután megnézhetjük az osztályozási jelentés kimenetét:

				precision    recall  f1-score   support

           0       0.83      0.91      0.87       316
           1       0.90      0.81      0.85       309

    accuracy                           0.86       625
   macro avg       0.86      0.86      0.86       625
weighted avg       0.86      0.86      0.86       625

Ez a mi eredményünk. Vedd észre precision, recall, f1-scoreés accuracy A mutatók mindegyike nagyon magas, 80% feletti, ami ideális – de ezeket az eredményeket valószínűleg a magas korrelációk befolyásolták, és hosszú távon nem maradnak fenn.

A modell pontossága 86%, ami azt jelenti, hogy az esetek 14%-ában téved a besorolásban. Rendelkezünk ezzel az általános információval, de érdekes lenne tudni, hogy a 14%-os hiba előfordul-e az osztályok besorolásával kapcsolatban 0 vagy osztály 1. Annak azonosítására, hogy mely osztályok melyikként vannak tévesen azonosítva, és milyen gyakorisággal – kiszámíthatjuk és ábrázolhatjuk a zavart mátrix modellünk előrejelzéseiből.

A modell értékelése zavarmátrixszal

Számítsuk ki, majd ábrázoljuk a zavaros mátrixot. Ezt követően minden részét megérthetjük. A zavaros mátrix ábrázolásához a Scikit-Learnt használjuk confusion_matrix(), amelyet importálunk a metrics modult.

A zavaros mátrix könnyebben megjeleníthető Seaborn használatával heatmap(). Tehát a generálás után a zavaró mátrixunkat adjuk át érvként a hőtérkép mellett:

from sklearn.metrics import confusion_matrix

cm = confusion_matrix(y_test, y_pred)
sns.heatmap(cm, annot=True, fmt='d')

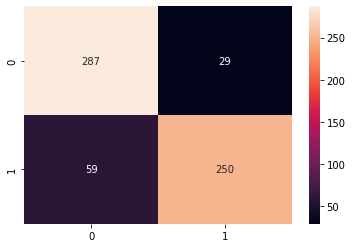
5. Zavart mátrix: a mátrix megmutatja, hogy a modell hány mintát kapott az egyes osztályokhoz. A helyes és helyesen megjósolt értékeket hívjuk igazi pozitívumok, és azokat, amelyeket pozitívnak jósoltak, de nem voltak pozitívak, az úgynevezett hamis pozitív. Ugyanaz a nómenklatúra igaz negatívumok és a hamis negatívok negatív értékekhez használják;

Ha megnézzük a zavaros mátrix diagramot, láthatjuk, hogy van 287 értékek voltak 0 és megjósolta mint 0 - vagy igazi pozitívumok órára 0 (a Çerçevelik magvak). Nekünk is van 250 igazi pozitívumok az osztály számára 1 (Ürgüp Sivrisi magvak). Az igazi pozitívumok mindig a mátrix átlójában találhatók, amely a bal felsőtől a jobb alsó felé halad.

Nekünk szintén van 29 értékek, amelyeknek lennie kellett volna 0, de megjósolta, mint 1 (hamis pozitív) És 59 értékek voltak 1 és megjósolta mint 0 (hamis negatívok). Ezekkel a számokkal megérthetjük, hogy a modell által elkövetett legnagyobb hiba az, hogy hamis negatívokat jósol. Tehát többnyire az Ürgüp Sivrisi magot Çerçevelik magnak minősítheti.

Ez a fajta hiba az osztály 81%-os felidézésével is magyarázható 1. Figyelje meg, hogy a mutatók össze vannak kapcsolva. A visszahívás különbsége pedig abból adódik, hogy az Ürgüp Sivrisi osztályból 100-zal kevesebb minta van. Ez az egyik következménye annak, ha csak néhány mintával kevesebb van, mint a másik osztályban. Az emlékezet további javítása érdekében kísérletezhet az osztálysúlyokkal, vagy használhat több Ürgüp Sivrisi mintát.

Eddig a legtöbb adattudományi hagyományos lépést végrehajtottuk, és fekete dobozként a logisztikus regressziós modellt használtuk.

Most itt az ideje, hogy kinyissa a fekete dobozt, és belenézzen, hogy mélyebben megértse a logisztikus regresszió működését.

Mélyebbre ható a logisztikai regresszió működése

A regresszió A szó nem véletlenül van ott, hogy megértsük, mit csinál a logisztikus regresszió, emlékezhetünk arra, mit tesz a testvére, a lineáris regresszió az adatokkal. A lineáris regressziós képlet a következő volt:

$$
y = b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + ldots + b_n * x_n
$$

Amelyben b₀ volt a regressziós metszéspont, b¹ az együttható és x¹ az adat.

Ez az egyenlet egy egyenest eredményezett, amelyet az új értékek előrejelzésére használtak. A bevezetőt felidézve a különbség most az, hogy nem új értékeket, hanem osztályt jósolunk. Tehát ezt az egyenest meg kell változtatni. A logisztikus regresszióval bevezetünk egy nemlinearitást, és az előrejelzést most egy görbe segítségével készítjük el vonal helyett:

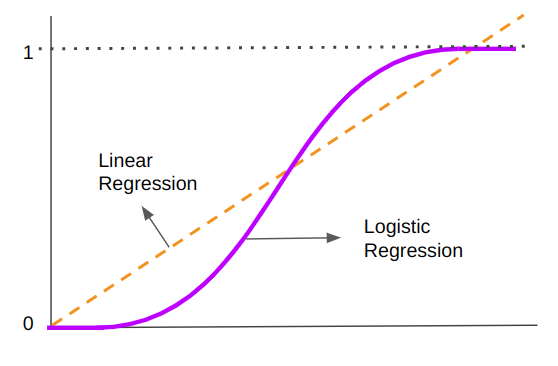
Figyeljük meg, hogy míg a lineáris regressziós egyenes folytatódik, és folytonos végtelen értékekből áll, addig a logisztikus regressziós görbe középre osztható, és szélsőértékei 0 és 1 értékben vannak. Ez az "S" alak az oka annak, hogy osztályozza az adatokat – a közelebb eső vagy a legmagasabb végpontra eső pontok az 1. osztályba tartoznak, míg az alsó kvadránsban vagy a 0-hoz közelebb eső pontok a 0 osztályba tartoznak. az „S” a 0 és 1 közötti középső, 0.5 – ez a logisztikus regressziós pontok küszöbe.

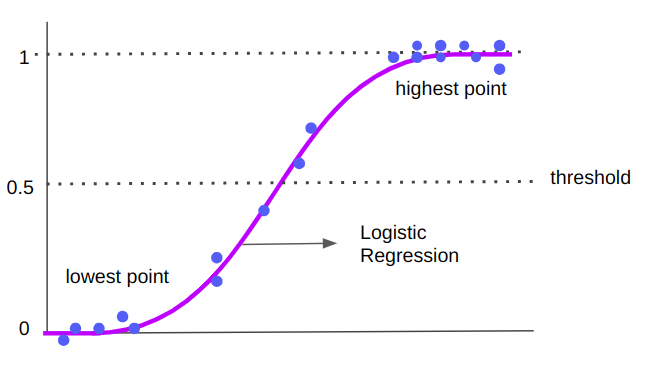
Már értjük a logisztikai és a lineáris regresszió vizuális különbségét, de mi a helyzet a képlettel? A logisztikus regresszió képlete a következő:

$$
y = b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + ldots + b_n * x_n
$$

Így is írható:

$$
y_{prob} = tört{1}{1 + e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + lpont + b_n * x_n)}}
$$

Vagy akár így is írható:

$$
y_{prob} = tört{e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + ldots + b_n * x_n)}}{1 + e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + ldots + b_n * x_n)}}
$$

A fenti egyenletben az értéke helyett a bemenet valószínűsége szerepel. Ennek számlálója 1, így 0 és 1 közötti értéket adhat, és 1 plusz egy értéket a nevezőjében, így értéke 1 és valami – ez azt jelenti, hogy a teljes tört eredmény nem lehet nagyobb 1-nél .

És mi az az érték, ami a nevezőben van? Ez e, a természetes logaritmus alapja (körülbelül 2.718282), a lineáris regresszió erejéig emelve:

$$
e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + ldots + b_n * x_n)}
$$

Az írás másik módja a következő lenne:

$$
ln bal (frac{p}{1-p} right) = {(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + ldots + b_n * x_n)}
$$

Az utolsó egyenletben ln a természetes logaritmus (e bázis) és p a valószínűség, tehát az eredmény valószínűségének logaritmusa megegyezik a lineáris regresszió eredményével.

Vagyis a lineáris regressziós eredménnyel és a természetes logaritmussal el lehet jutni annak a valószínűségéhez, hogy egy tervezett osztályhoz tartozó vagy nem bemeneti adat.

A teljes logisztikus regresszió levezetési folyamat a következő:

$$
p{X} = frak{e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + ldots + b_n * x_n)}}{1 + e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + ldots + b_n * x_n)}}
$$

$$
p(1 + e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + lpont + b_n * x_n)}) = e^{(b_0 + b_1 * x_1 + b_2 *x_2 + b_3 * x_3 + lpont + b_n * x_n)}
$$

$$
p + p*e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + lpont + b_n * x_n)} = e^{(b_0 + b_1 * x_1 + b_2 *x_2 + b_3 * x_3 + lpont + b_n * x_n)}
$$

p
=

e

(

b
0

+

b
1

*

x
1

+

b
2

*

x
2

+

b
3

*

x
3

+
...
+

b
n

*

x
n

)

-
p
*

e

(

b
0

+

b
1

*

x
1

+

b
2

*

x
2

+

b
3

*

x
3

+
...
+

b
n

*

x
n

)

$$
frac{p}{1-p} = e^{(b_0 + b_1 * x_1 + b_2 *x_2 + b_3 * x_3 + ldots + b_n * x_n)}
$$

$$
ln bal (frac{p}{1-p} right) = (b_0 + b_1 * x_1 + b_2 *x_2 + b_3 * x_3 + ldots + b_n * x_n)
$$

Ez azt jelenti, hogy a logisztikus regressziós modellnek együtthatói és metszésponti értéke is van. Mivel lineáris regressziót használ, és hozzáad egy nemlineáris komponenst a természetes logaritmussal (e).

A modellünk együtthatóinak és metszőpontjának értékeit ugyanúgy láthatjuk, mint a lineáris regressziónál, coef_ és a intercept_ tulajdonságok:

logreg.coef_

Ez megjeleníti a 12 jellemző mindegyikének együtthatóit:

array([[ 1.43726172, -1.03136968,  0.24099522, -0.61180768,  1.36538261,
        -1.45321951, -1.22826034,  0.98766966,  0.0438686 , -0.78687889,
         1.9601197 , -1.77226097]])

logreg.intercept_

Ennek eredménye:

array([0.08735782])

Az együtthatók és a metszéspontértékek segítségével kiszámíthatjuk adataink előre jelzett valószínűségeit. Vegyük az elsőt X_test példaként ismét értékek:

X_test[:1]

Ezzel visszaadja az első sort X_test NumPy tömbként:

array([[-1.09830823, -0.93651823, -0.60794138, -1.13255059, -1.0827684 ,
        -1.12235877,  0.45891056, -1.07825898,  0.56284738, -0.17604099,
         0.23661678, -0.36013424]])

A kezdeti egyenletet követve:

$$
p{X} = frak{e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + ldots + b_n * x_n)}}{1 + e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + ldots + b_n * x_n)}}
$$

A pythonban a következők vannak:

import math

lin_reg = logreg.intercept_[0] + 
((logreg.coef_[0][0]* X_test[:1][0][0])+ 
(logreg.coef_[0][1]* X_test[:1][0][1])+ 
(logreg.coef_[0][2]* X_test[:1][0][2])+ 
(logreg.coef_[0][3]* X_test[:1][0][3])+ 
(logreg.coef_[0][4]* X_test[:1][0][4])+ 
(logreg.coef_[0][5]* X_test[:1][0][5])+ 
(logreg.coef_[0][6]* X_test[:1][0][6])+ 
(logreg.coef_[0][7]* X_test[:1][0][7])+ 
(logreg.coef_[0][8]* X_test[:1][0][8])+ 
(logreg.coef_[0][9]* X_test[:1][0][9])+ 
(logreg.coef_[0][10]* X_test[:1][0][10])+ 
(logreg.coef_[0][11]* X_test[:1][0][11]))

px = math.exp(lin_reg)/(1 +(math.exp(lin_reg)))
px

Ennek eredményeként:

0.45273372469369133

Ha újra megnézzük a predict_proba az első eredménye X_test sorunk van:

logreg.predict_proba(X_test[:1])

Ez azt jelenti, hogy az eredeti logisztikus regressziós egyenlet megadja az osztályra vonatkozó bemenet valószínűségét 1, hogy megtudja, melyik valószínűség az osztályra 0, egyszerűen:

1 - px

Vedd észre, hogy mindkettő px és a 1-px azonosak predict_proba eredmények. Így és miért történik a logisztikus regresszió kiszámítása regresszió nevének része. De mi a helyzet a kifejezéssel logisztikai?

A kifejezés logisztikai származik logit, amely egy olyan függvény, amelyet már láttunk:

$$
bal oldalon (frac{p}{1-p} jobb)
$$

Most számoltunk vele px és a 1-px. Ez a logit, más néven log-odds mivel egyenlő az esélyek logaritmusával ahol p egy valószínűség.

Következtetés

Ebben az útmutatóban az egyik legalapvetőbb gépi tanulási osztályozási algoritmust tanulmányoztuk, pl logisztikus regresszió.

Kezdetben a logisztikus regressziót fekete dobozként valósítottuk meg a Scikit-Learn gépi tanulási könyvtárával, majd később lépésről lépésre megértettük, hogy egyértelmű legyen, miért és honnan ered a regresszió és a logisztika kifejezés.

Feltártuk és tanulmányoztuk az adatokat is, megértve, hogy ez az adattudományi elemzés egyik legfontosabb része.

Innentől azt tanácsolom, hogy játsszon vele többosztályú logisztikai regresszió, logisztikus regresszió kettőnél több osztályhoz – ugyanazt a logisztikus regressziós algoritmust alkalmazhatja más, több osztályú adatkészletekhez is, és értelmezheti az eredményeket.

Azt is tanácsolom, hogy tanulmányozza az L1 és L2 rendszeresítések, ezek egy módja annak, hogy a magasabb adatokat „büntesse” annak érdekében, hogy azok közelebb kerüljenek a normálhoz, kitartva a modell komplexitását, így az algoritmus jobb eredményt érhet el. Az általunk használt Scikit-Learn implementáció alapértelmezés szerint már L2 rendszerezéssel rendelkezik. A másik dolog, amit meg kell nézni, az a másság megoldók, Mint például a lbgs, amelyek optimalizálják a logisztikus regressziós algoritmus teljesítményét.

Fontos még egy pillantást vetni a statisztikai logisztikai regresszió megközelítése. Megvan feltételezések az adatok viselkedéséről és egyéb statisztikákról, amelyeknek meg kell őrizniük a kielégítő eredményeket, mint például:

• a megfigyelések függetlenek;
• a magyarázó változók között nincs multikollinearitás;
• nincsenek szélsőséges kiugró értékek;
• lineáris kapcsolat van a magyarázó változók és a válaszváltozó logitja között;
• a minta mérete kellően nagy.

Figyelje meg, hány ilyen feltevés szerepelt már elemzésünkben és adatkezelésünkben.

Remélem, továbbra is feltárja, mit kínál a logisztikai regresszió az összes különböző megközelítésében!