Elliptikus görbe „Murmurációkat” találtak a mesterséges intelligenciával Take Flight | Quanta Magazin

Az elliptikus görbék a modern matematika legcsábítóbb objektumai közé tartoznak. Nem tűnnek bonyolultnak, de gyorsforgalmi utat képeznek a sokak által középiskolában tanult matematika és a matematikai kutatások között a legbonyolultabb formájában. Ezek központi szerepet játszottak Andrew Wiles Fermat utolsó tételének ünnepelt bizonyításában az 1990-es években. Ezek a modern kriptográfia kulcsfontosságú eszközei. 2000-ben pedig a Clay Mathematics Institute elnevezett a sejtés a statisztikákkal kapcsolatban Az elliptikus görbék egyike a hét „Millennium Prize Probléma” közül, amelyek mindegyikének megoldásáért 1 millió dollár jutalom jár. Ez a sejtés, amelyre először vállalkozott Bryan Birch és a Peter Swinnerton-Dyer az 1960-as években, még mindig nem sikerült bebizonyítani.

Az elliptikus görbék megértése nagy téttel bíró törekvés, amely központi szerepet játszott a matematikában. Így 2022-ben, amikor egy transzatlanti együttműködés statisztikai technikákat és mesterséges intelligenciát használt, hogy teljesen váratlan mintákat fedezzen fel az elliptikus görbékben, ez üdvözlendő, ha váratlan is volt. „Csak idő kérdése volt, hogy a gépi tanulás mikor kerül a küszöbünkre valami érdekességgel” – mondta Sarnak Péter, az Institute for Advanced Study és a Princeton Egyetem matematikusa. Kezdetben senki sem tudta megmagyarázni, miért léteznek az újonnan felfedezett minták. Azóta egy sor újabb tanulmányban a matematikusok elkezdték feltárni a minták mögött meghúzódó okokat, amelyeket „mormolásnak” neveztek el a seregélyek folyékony alakjához való hasonlóságuk miatt, és elkezdték bizonyítani, hogy ezeknek nem csak az adott területen kell előfordulniuk. 2022-ben vizsgált példák, de általánosabban elliptikus görbékben.

Az elliptikus lét fontossága

Ahhoz, hogy megértsük, melyek ezek a minták, egy kis alapot kell lefektetnünk azzal kapcsolatban, hogy mik is azok az elliptikus görbék, és hogyan kategorizálják őket a matematikusok.

Az elliptikus görbe egy változó négyzetére vonatkozik, amelyet általában így írnak le y, a másik harmadik hatványára, általában így írják x: y² = x³ + Ax + B, néhány számpárhoz A és a B, Mindaddig, amíg A és a B megfelel néhány egyszerű feltételnek. Ez az egyenlet egy görbét határoz meg, amely a síkon ábrázolható, az alábbiak szerint. (A nevek hasonlósága ellenére az ellipszis nem elliptikus görbe.)

Bár az egyszerűnek tűnő, elliptikus görbék hihetetlenül hatékony eszközöknek bizonyulnak a számelméleti szakemberek számára – azoknak a matematikusoknak, akik az egész számokban keresnek mintákat. Ahelyett, hogy hagyná a változókat x és a y A matematikusok előszeretettel korlátozzák ezeket a különböző számrendszerekre, amelyeket egy adott számrendszer feletti görbe meghatározásának neveznek. A racionális számokra korlátozódó elliptikus görbék – olyan számok, amelyek törtként írhatók fel – különösen hasznosak. „A valós vagy komplex számok feletti elliptikus görbék meglehetősen unalmasak” – mondta Sarnak. "Csak a racionális számok mélyek."

Íme, egy módszer, ami igaz. Ha egy elliptikus görbén két racionális pont közé húzunk egy egyenest, akkor az a hely is racionális lesz, ahol az egyenes metszi a görbét. Ezt a tényt felhasználhatja az „összeadás” meghatározására egy elliptikus görbében, az alábbiak szerint.

Húzz egy vonalat közé P és a Q. Ez a vonal egy harmadik pontban metszi a görbét, R. (A matematikusoknak van egy speciális trükkjük arra az esetre, amikor az egyenes nem metszi a görbét, hozzáadva egy „pont a végtelenben”.) A reflexió R az egész x-tengely az összeged P + Q. Ezzel az összeadási művelettel együtt a görbe összes megoldása egy csoportnak nevezett matematikai objektumot alkot.

A matematikusok ezt használják a görbe „rangsorának” meghatározására. A görbe rangja a racionális megoldások számára vonatkozik. A 0. rangú görbéknek véges számú megoldása van. A magasabb rangú görbéknek végtelen számú megoldása van, amelyek egymáshoz való viszonyát az összeadási művelettel a rang írja le.

A rangokat nem értik jól; A matematikusok nem mindig tudják kiszámítani ezeket, és nem tudják, mekkora lehet. (Egy adott görbére ismert legnagyobb pontos rangsor a 20.) A hasonló megjelenésű görbéknek teljesen eltérő rangjai lehetnek.

Az elliptikus görbéknek is sok köze van a prímszámokhoz, amelyek csak 1-gyel és önmagukkal oszthatók. A matematikusok különösen a véges mezők görbéit vizsgálják – ciklikus aritmetikai rendszereket, amelyeket minden prímszámhoz definiálnak. A véges mező olyan, mint egy óra, amelynek órák száma megegyezik a prímszámmal: Ha folyamatosan felfelé számol, a számok elölről kezdődnek. Például a 7 véges mezőjében 5 plusz 2 egyenlő nullával, és 5 plusz 3 egyenlő 1-gyel.

Egy elliptikus görbéhez tartozik egy számsor, ún a_p, ami a prím által meghatározott véges mező görbéjének megoldásainak számára vonatkozik. p. Egy kisebb a_p több megoldást jelent; egy nagyobb a_p kevesebb megoldást jelent. Bár a rangot nehéz kiszámítani, a sorrendet a_p sokkal könnyebb.

Az egyik legelső számítógépen végzett számos számítás alapján Birch és Swinnerton-Dyer összefüggést sejtett egy elliptikus görbe rangja és a sorozat között. a_p. Bárki, aki be tudja bizonyítani, hogy igaza volt, egymillió dollárt és matematikai halhatatlanságot nyerhet.

Meglepetés minta jelenik meg

A járvány kezdete után Yang-Hui He, a London Institute for Mathematical Sciences kutatója úgy döntött, hogy új kihívásokkal néz szembe. A főiskolán fizika szakon végzett, és a Massachusetts Institute of Technology-n szerzett doktori fokozatot matematikai fizikából. De egyre jobban érdekelte a számelmélet, és tekintettel a mesterséges intelligencia növekvő képességeire, úgy gondolta, kipróbálja magát a mesterséges intelligencia használatában, hogy váratlan számmintákat találjon. (Már volt gépi tanulás segítségével osztályozni Calabi-Yau elosztó, a húrelméletben széles körben használt matematikai struktúrák.)

2020 augusztusában, a járvány elmélyülésével a Nottinghami Egyetem vendégül látta őt. online beszélgetés. Pesszimista volt a fejlődésével kapcsolatban, és azzal kapcsolatban, hogy a gépi tanulás segítségével új matematikai ismereteket fedezhet fel. „Az ő narratívája az volt, hogy a számelmélet nehéz volt, mert a számelméletben nem lehet gépi tanulást végezni” – mondta. Thomas Oliver, a Westminsteri Egyetem matematikusa, aki ott volt a hallgatóság körében. Ahogy emlékszik: „Nem találtam semmit, mert nem voltam szakértő. Még csak nem is a megfelelő dolgokat használtam, hogy ezt nézzem.”

Olivér és Kyu-Hwan Lee, a Connecticuti Egyetem matematikusa kezdett együtt dolgozni He. „Úgy döntöttünk, hogy ezt csak azért tesszük, hogy megtanuljuk, mi az a gépi tanulás, nem pedig azért, hogy komolyan tanuljuk a matematikát” – mondta Oliver. – De gyorsan rájöttünk, hogy sok mindent meg lehet tanulni géppel.

Oliver és Lee azt javasolták, hogy alkalmazza a technikáit a vizsgálatra L-függvények, a sorozaton keresztül az elliptikus görbékhez szorosan kapcsolódó végtelen sorozatok a_p. Használhatnának egy online adatbázist az elliptikus görbékről és a kapcsolódó görbékről L-függvények az úgynevezett LMFDB hogy képezzék gépi tanulási osztályozóikat. Abban az időben az adatbázis valamivel több mint 3 millió elliptikus görbét tartalmazott a racionális értékek felett. 2020 októberére megvoltak egy papír amelyből leszűrt információkat használtak fel L-függvények az elliptikus görbék egy adott tulajdonságának előrejelzésére. Novemberben osztoztak újabb papír amely gépi tanulást használt más objektumok számelméleti osztályozására. Decemberre sikerült megjósolni az elliptikus görbék sorait nagy pontossággal.

De nem voltak biztosak benne, miért működnek olyan jól a gépi tanulási algoritmusaik. Lee megkérte egyetemi hallgatóját, Alekszej Pozdnyakovot, hátha rájön, mi történik. Amint megtörténik, az LMFDB az elliptikus görbéket a vezetőnek nevezett mennyiség szerint rendezi, amely összefoglalja azokat a prímeket, amelyeknél a görbe nem működik megfelelően. Tehát Pozdnyakov megpróbált egyszerre nagyszámú görbét megvizsgálni hasonló vezetőkkel – mondjuk az összes görbét 7,500 és 10,000 közötti vezetőkkel.

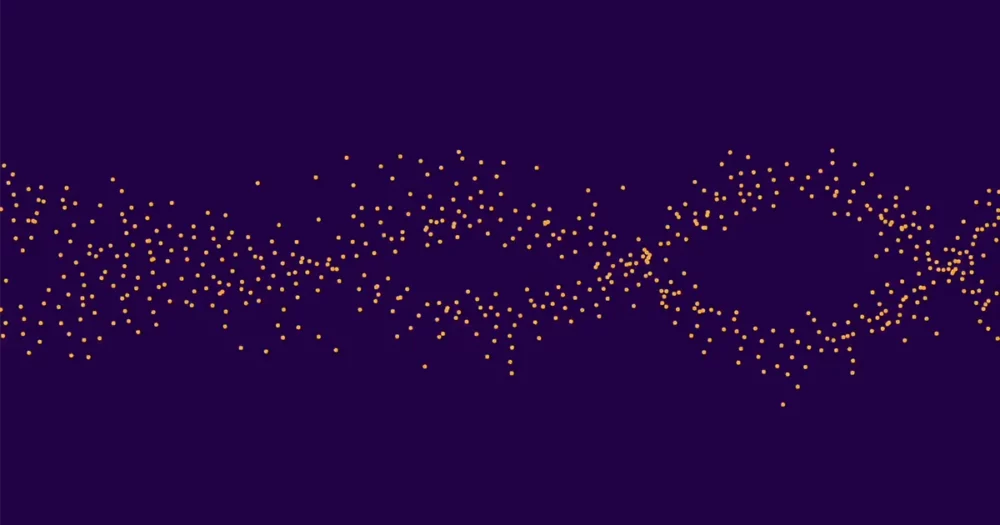
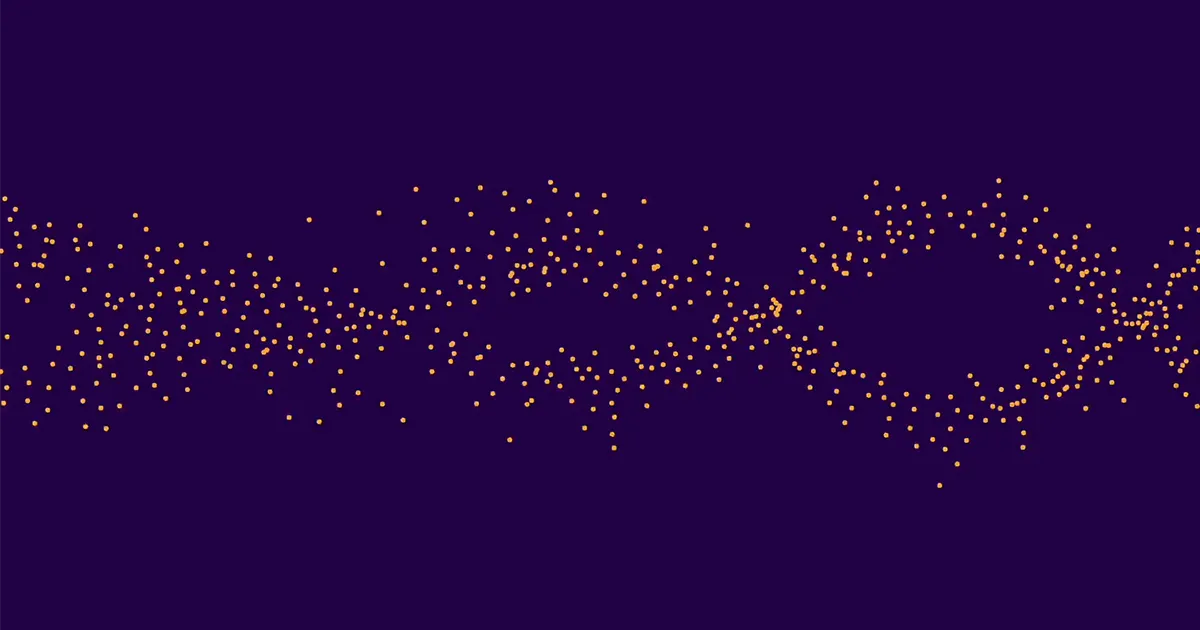
Ez összesen körülbelül 10,000 0 görbét jelentett. Ezek körülbelül fele 1-s, fele XNUMX-es rangú volt. (A magasabb rangok rendkívül ritkák.) Ezután átlagolta a a_p az összes 0. rangú görbére, külön átlagolva a_p az összes 1. rangú görbére, és ábrázoltuk az eredményeket. A két ponthalmaz két különálló, könnyen felismerhető hullámot alkotott. Ezért tudták a gépi tanulási osztályozók helyesen megállapítani az egyes görbék rangsorát.

„Először csak örültem, hogy teljesítettem a feladatot” – mondta Pozdnyakov. "De Kyu-Hwan azonnal felismerte, hogy ez a minta meglepő, és ekkor vált igazán izgalmassá."

Lee és Oliver el voltak ragadtatva. – Alexey megmutatta nekünk a képet, és én azt mondtam, hogy úgy néz ki, mint a madarak – mondta Oliver. "És akkor Kyu-Hwan utánanézett, és azt mondta, hogy ezt mormolásnak hívják, majd Yang azt mondta, hívjuk fel az újságot.Elliptikus görbék mormolásai.”

2022 áprilisában töltötték fel dolgozatukat, és továbbították néhány másik matematikusnak, idegesen várva, hogy elmondják nekik, hogy az úgynevezett „felfedezésük” közismert. Oliver azt mondta, hogy a kapcsolat annyira látható volt, hogy már régen észre kellett volna venni.

Az előnyomat szinte azonnal felkeltette az érdeklődést, különösen azoktól Andrew Sutherland, az MIT kutatója, az LMFDB egyik vezető szerkesztője. Sutherland rájött, hogy 3 millió elliptikus görbe nem elég a céljaihoz. Sokkal nagyobb vezetéktartományokat akart megnézni, hogy lássa, milyen erős a zörej. Adatokat gyűjtött egy másik hatalmas, körülbelül 150 millió elliptikus görbét tartalmazó adattárból. Még mindig elégedetlen volt, majd egy másik adattárból gyűjtött be adatokat 300 millió görbével.

„De még ezek sem voltak elegek, így valójában egy több mint egymilliárd elliptikus görbéből álló új adathalmazt számoltam ki, és ezt használtam a valóban nagy felbontású képek kiszámításához” – mondta Sutherland. A zörejekből kiderült, hogy egyszerre több mint 15,000 XNUMX elliptikus görbét átlagolt-e, vagy egyszerre milliót. Az alak akkor is ugyanaz maradt, amikor egyre nagyobb prímszámok görbéit nézte, ezt a jelenséget skálainvarianciának nevezik. Sutherland arra is rájött, hogy a zörejek nem csak az elliptikus görbékre jellemzőek, hanem általánosságban is megjelennek L- funkciókat. Írt megállapításait összefoglaló levelet és elküldte Sarnaknak és Michael Rubinstein a Waterloo Egyetemen.

„Ha van rá ismert magyarázat, azt remélem, tudni fogod” – írta Sutherland.

Nem tették.

A minta magyarázata

Lee, He és Oliver 2023 augusztusában workshopot szervezett a zörejekről a Brown Egyetem Számítógépes és Kísérleti Kutatási Intézetében (ICERM). Sarnak és Rubinstein jött, ahogy Sarnak tanítványa is Nina Zubrilina.

Zubrilina bemutatta a zúgolódási mintákkal kapcsolatos kutatásait moduláris formák, speciális komplex függvények, amelyek az elliptikus görbékhez hasonlóan társítottak L- funkciókat. A nagy vezetőkkel rendelkező moduláris formákban a zörejek egy élesen meghatározott görbévé konvergálnak, ahelyett, hogy észrevehető, de szétszórt mintát alkotnának. Ban ben egy papír A 11. október 2023-én közzétett cikkben Zubrilina bebizonyította, hogy az ilyen típusú zúgolódás az általa felfedezett kifejezett képletet követi.

„Nina nagy eredménye, hogy erre adott egy képletet; Én ezt a Zubrilina zúgássűrűség képletnek nevezem” – mondta Sarnak. "Nagyon kifinomult matematikával bebizonyított egy pontos képletet, amely tökéletesen illeszkedik az adatokhoz."

A képlete bonyolult, de Sarnak fontos, új típusú függvényként értékeli, amely összevethető az Airy-függvényekkel, amelyek a fizika különféle kontextusaiban használt differenciálegyenletek megoldásait határozzák meg, az optikától a kvantummechanikáig.

Bár Zubrilina formulája volt az első, mások követték. „Mostantól minden héten megjelenik egy új lap – mondta Sarnak –, amely főként Zubrilina eszközeit használja, és a zúgolódás egyéb vonatkozásait magyarázza el.

Jonathan Bober, Andrew Booker és a Min lee a Bristoli Egyetemen, együtt David Lowry-Duda Az ICERM tanulmánya bebizonyította, hogy létezik egy másik típusú mormogás moduláris formában újabb októberi lap. És Kyu-Hwan Lee, Oliver és Pozdnyakov bebizonyította a létezését a Dirichlet-karaktereknek nevezett tárgyakban zajló mormolásokról, amelyekhez szorosan kapcsolódik L- funkciókat.

Sutherlandet lenyűgözte az a jelentős adag szerencse, amely a zúgolódások felfedezéséhez vezetett. Ha az elliptikus görbe adatait nem a vezető rendelte volna el, a zörejek eltűntek volna. "Szerencséjük volt, hogy az LMFDB-től vettek adatokat, amelyek a karmester szerint előre válogatva érkeztek" - mondta. „Ez kapcsolja össze az elliptikus görbét a megfelelő moduláris formával, de ez egyáltalán nem nyilvánvaló. … Két görbe, amelyek egyenlete nagyon hasonlónak tűnik, nagyon eltérő vezetőkkel rendelkezhet.” Például Sutherland megjegyezte, hogy y² = x³ - 11x + 6-nak van 17-es vezetéke, de a mínusz jelet pluszjelre fordítja, y² = x³ + 11x + 6-nak 100,736 XNUMX-os vezetéke van.

Már akkor is csak Pozdnyakov tapasztalatlansága miatt találták meg a zúgolódásokat. – Nem hiszem, hogy megtaláltuk volna nélküle – mondta Oliver –, mert a szakértők hagyományosan normalizálják a_p hogy abszolút értéke legyen 1. De nem normalizálta őket… szóval az oszcillációk nagyon nagyok és láthatóak voltak.”

Azok a statisztikai minták, amelyeket az AI algoritmusok használnak az elliptikus görbék rangsor szerinti rendezésére, egy több száz dimenziójú paramétertérben léteznek – túl sok ahhoz, hogy az emberek fejükben át tudják válogatni, nemhogy vizualizálni – jegyezte meg Oliver. De bár a gépi tanulás megtalálta a rejtett oszcillációkat, „csak később értettük meg, hogy ezek a mormogás”.

A szerkesztő megjegyzése: Andrew Sutherland, Kyu-Hwan Lee és az L-függvények és moduláris űrlapok adatbázisa (LMFDB) kapott támogatást a Simons Alapítványtól, amely szintén finanszírozza ezt a szerkesztőileg független kiadványt. A Simons Foundation finanszírozási döntései nincsenek hatással a fedezetünkre. További információ áll rendelkezésre itt.