Az új áttörés a mátrixszorzást közelebb hozza az ideálishoz | Quanta Magazin

Az informatikusok igényes csapatot alkotnak. Számukra nem elég, ha megfelelő választ kapnak egy problémára – a cél szinte mindig az, hogy a lehető leghatékonyabban kapják meg a választ.

Vegyük a mátrixok vagy számtömbök szorzását. 1812-ben Jacques Philippe Marie Binet francia matematikus kidolgozta azt az alapvető szabályrendszert, amelyet ma is tanítunk a diákoknak. Tökéletesen működik, de más matematikusok találtak módot a folyamat egyszerűsítésére és felgyorsítására. Most a feladat a folyamat felgyorsítása A mátrixszorzás a matematika és a számítástechnika metszéspontjában fekszik, ahol a kutatók a mai napig folytatják a folyamat javítását – bár az elmúlt évtizedekben a javulás meglehetősen szerény volt. 1987 óta a mátrixszorzás számszerű javulása „kicsi és… rendkívül nehezen elérhető” – mondta. François Le Gall, a Nagoya Egyetem informatikusa.

Most három kutató – Ran Duan és Renfei Zhou a Tsinghua Egyetemről, valamint Hongxun Wu a Kaliforniai Egyetemről, Berkeley – jelentős lépést tett előre ennek az örökkévaló probléma leküzdésében. Az övék új eredmények, amelyet tavaly novemberben mutattak be a Számítástudomány alapjai konferencián, egy váratlan új technikából erednek – mondta Le Gall. Bár maga a javulás viszonylag kicsi volt, Le Gall „koncepcionálisan nagyobbnak nevezte, mint más korábbiak”.

A technika egy korábban ismeretlen, ezért kiaknázatlan potenciális fejlesztési forrást tár fel, és már meghozta gyümölcsét: Egy második papírA januárban megjelent cikk az elsőre épít, amely bemutatja, hogyan lehet még tovább fokozni a mátrixszorzást.

„Ez egy jelentős technikai áttörés” – mondta Vilmos Kuszmaul, a Harvard Egyetem elméleti informatikusa. "Ez a legnagyobb előrelépés a mátrixszorzásban, amit több mint egy évtizede láttunk."

Lépjen be a Mátrixba

Talán homályos problémának tűnik, de a mátrixszorzás alapvető számítási művelet. Beépült az algoritmusok nagy részébe, amelyeket az emberek mindennap különféle feladatokhoz használnak, az élesebb számítógépes grafika megjelenítésétől a hálózatelméleti logisztikai problémák megoldásáig. És mint a számítás más területein, itt is a sebesség a legfontosabb. Még az enyhe fejlesztések is jelentős idő-, számítási teljesítmény- és pénzmegtakarítást eredményezhetnek. De egyelőre az elméleti szakembereket elsősorban az érdekli, hogy kitalálják, milyen gyors lehet a folyamat.

A kettő szorzásának hagyományos módja n-által-n mátrixok – az első mátrix minden sorából származó számok és a második mátrix oszlopaiban lévő számok szorzásával – megköveteli n³ külön szorzások. A 2-szeres mátrixoknál ez 2-t jelent³ vagy 8 szorzás.

1969-ben Volker Strassen matematikus feltárt egy bonyolultabb eljárást, amely 2-2 mátrixot képes megszorozni mindössze hét szorzási lépésben és 18 összeadással. Két évvel később Shmuel Winograd informatikus bebizonyította, hogy a hét valóban az abszolút minimum a 2x2-es mátrixokhoz.

Strassen ugyanazt az ötletet használta ki, hogy megmutassa, hogy mindez nagyobb n-által-n mátrixok is szorozhatók kevesebb mint n³ lépések. Ennek a stratégiának a kulcseleme a dekompozíciónak nevezett eljárás – egy nagy mátrix felosztása egymás után kisebb részmátrixokra, amelyek akár 2-szeres vagy akár 2-szeres méretűek is lehetnek (ezek csak egyetlen számok).

Egy óriási tömb apró darabokra való felosztásának indoklása meglehetősen egyszerű Virginia Vassilevska Williams, a Massachusetts Institute of Technology informatikusa és az egyik új tanulmány társszerzője. „Nehéz az embernek egy nagy mátrixot nézni (mondjuk 100x100-as nagyságrendben), és a lehető legjobb algoritmusra gondolni” – mondta Vassilevska Williams. Még a 3x3 mátrixok sem lettek teljesen megoldva. "Mindazonáltal használhatunk kis mátrixokhoz már kifejlesztett gyors algoritmust, hogy nagyobb mátrixokhoz is kapjanak gyors algoritmust."

A kutatók megállapították, hogy a sebesség kulcsa a szorzási lépések számának csökkentése, a kitevő csökkentése n³ (a standard módszernél) amennyit csak tudnak. A lehető legalacsonyabb érték, n², alapvetően annyi, amennyire csak a válasz megírása szükséges. Az informatikusok ezt a kitevőt omega-nak, ω-nek nevezik n^ω lévén a lehető legkevesebb lépés szükséges a kettő sikeres szorzásához n-által-n mátrixok mint n nagyon nagyra nő. „Ennek a munkának az a lényege – mondta Zhou, aki a 2024. januári tanulmány társszerzője is –, hogy megnézzük, milyen közel kerülhet a 2-hez, és hogy ez elméletben elérhető-e.

Lézeres fókusz

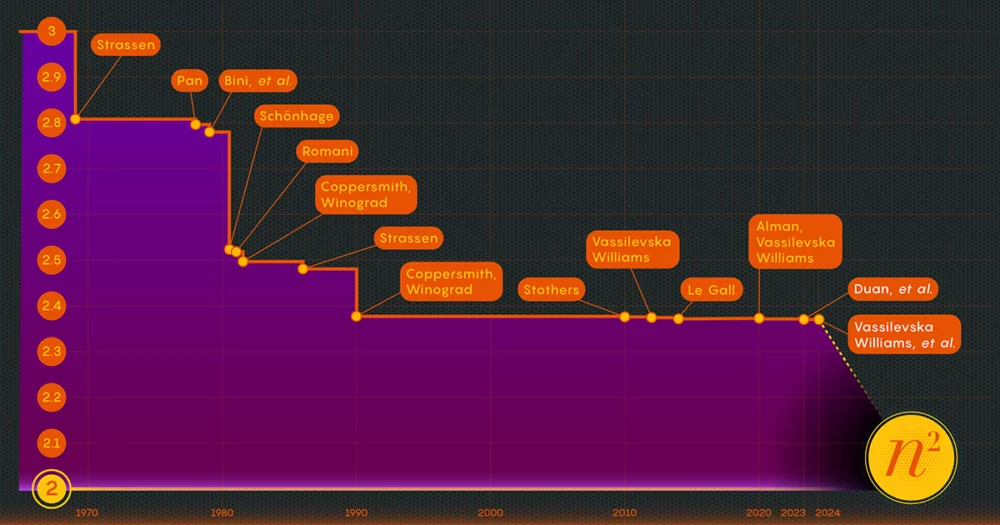
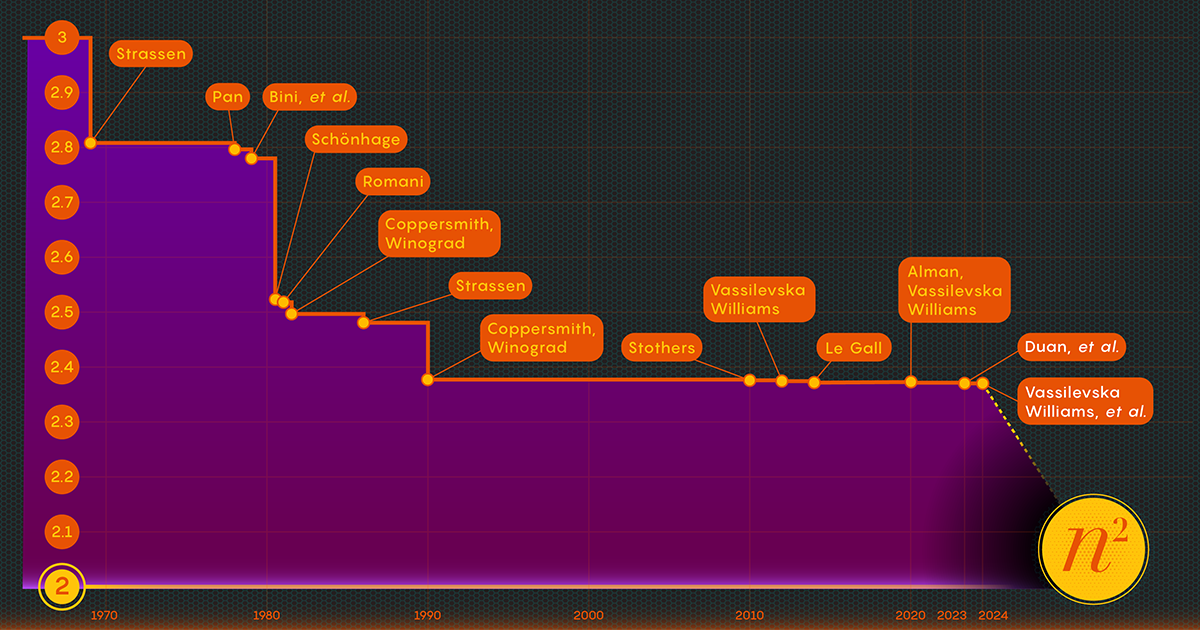
1986-ban Strassen újabb nagy áttörést ért el, amikor ő Bevezetett amit mátrixszorzás lézeres módszerének neveznek. Strassen ezt használta az omega 2.48 felső értékének megállapítására. Bár a módszer csak egy lépés a nagy mátrixszorzásban, az egyik legfontosabb, mert a kutatók folyamatosan fejlesztették.

Egy évvel később Winograd és Don Coppersmith egy új algoritmust vezetett be, amely gyönyörűen kiegészítette a lézeres módszert. Az eszközöknek ez a kombinációja szinte minden későbbi, a mátrixszorzás felgyorsítására irányuló erőfeszítésben szerepelt.

Íme egy leegyszerűsített gondolkodásmód arról, hogy ezek a különböző elemek hogyan illeszkednek egymáshoz. Kezdjük két nagy mátrixszal, A-val és B-vel, amelyeket össze akarunk szorozni. Először is fel kell bontani őket sok kisebb részmátrixra vagy blokkra, ahogy néha nevezik. Ezután használhatja a Coppersmith és Winograd algoritmusát, amely egyfajta használati útmutatóként szolgál a blokkok kezeléséhez és végül összeszereléséhez. „Megmondja, hogy mit kell szorozni és mit kell hozzáadni, és milyen bejegyzések hova kerülnek” a C termékmátrixban – mondta Vassilevska Williams. "Ez csak egy recept a C felépítéséhez A-ból és B-ből."

Van azonban egy bökkenő: néha olyan blokkokhoz jutsz, amelyeknek közös bejegyzései vannak. Ha ezeket a termékben hagyná, az olyan lenne, mintha kétszer számolná meg ezeket a bejegyzéseket, tehát egy bizonyos ponton meg kell szabadulnia az ismétlődő kifejezésektől, az úgynevezett átfedésektől. A kutatók ezt úgy teszik meg, hogy „megölik” azokat a blokkokat, amelyekben vannak – nullára állítják összetevőiket, hogy eltávolítsák őket a számításból.

Itt lép be végre Strassen lézeres módszere. "A lézeres módszer általában nagyon jól működik, és általában jó módszert talál a blokkok egy részhalmazának megölésére, hogy eltávolítsa az átfedést" - mondta Le Gall. Miután a lézer megszüntette vagy „elégette” az összes átfedést, elkészítheti a C végtermékmátrixot.

Ha ezeket a különféle technikákat összeállítjuk, akkor egy olyan algoritmust kapunk, amely két mátrixot szándékosan csekély számú szorzással összeszoroz – legalábbis elméletben. A lézeres módszernek nem célja, hogy praktikus legyen; ez csak egy módja annak, hogy átgondoljuk a mátrixok szorzásának ideális módját. "Soha nem futtatjuk a módszert [számítógépen]" - mondta Zhou. – Elemezzük.

És ez az elemzés vezetett az omega legnagyobb javulásához az elmúlt több mint egy évtizedben.

Veszteséget találtak

Duan, Zhou és Wu tavaly nyári lapja kimutatta, hogy Strassen folyamata még mindig jelentősen felgyorsítható. Mindez annak a koncepciónak köszönhető, amelyet rejtett veszteségnek neveztek, és amely a korábbi elemzések mélyén el van temetve – „a túl sok blokk akaratlan megölésének eredménye” – mondta Zhou.

A lézeres módszer úgy működik, hogy az átfedő blokkokat szemétként címkézi, amelyeket ártalmatlanításra szántak; a többi blokkot érdemesnek tekintik, és megmentik. A kiválasztási folyamat azonban némileg véletlenszerű. Egy szemétnek minősített blokk valójában hasznosnak bizonyulhat. Ez nem volt teljesen meglepetés, de sok ilyen véletlenszerű választást megvizsgálva Duan csapata megállapította, hogy a lézeres módszer szisztematikusan alulértékeli a blokkokat: Több blokkot kell megmenteni és kevesebbet kidobni. És ahogy általában lenni szokott, a kevesebb hulladék nagyobb hatékonyságot eredményez.

„Ha több blokkot tudunk tartani átfedés nélkül, az… gyorsabb mátrixszorzó algoritmust eredményez” – mondta Le Gall.

Miután bebizonyította a veszteség létezését, Duan csapata módosította a lézeres módszerrel a blokkok feliratozását, jelentősen csökkentve ezzel a hulladékot. Ennek eredményeként az omega új felső határát 2.371866 körül határozták meg, ami előrelépés a korábbi, 2.3728596-os felső határhoz képest. 2020-ben játszódik Josh Alman és Vassilevska Williams. Ez szerény változásnak tűnhet, mindössze 0.001-gyel csökkenti a korlátot. De ez az egyetlen legnagyobb javulás, amit a tudósok 2010 óta tapasztaltak. Vassilevska Williams és Alman 2020-as eredménye ehhez képest csak 0.00001-rel javult elődjéhez képest.

A kutatók számára azonban nem csak az új rekord a legizgalmasabb – ami nem tartott sokáig. Ez az a tény is, hogy a lap felfedte a fejlődés új útját, amely addig teljesen észrevétlen volt. Közel négy évtizede mindenki ugyanarra a lézeres módszerre támaszkodik, mondta Le Gall. "Aztán rájöttek, hogy nos, tudunk jobban csinálni."

A 2024. januári tanulmány finomította ezt az új megközelítést, lehetővé téve Vassilevska Williamsnek, Zhounak és szerzőtársaiknak, hogy tovább csökkentsék a rejtett veszteséget. Ez az omega felső határának további javulásához vezetett, 2.371552-re csökkentve. A szerzők ugyanezt a technikát általánosították, hogy javítsák a szorzási folyamatot négyszögletes (n-által-m) mátrixok – olyan eljárás, amely a gráfelméletben, a gépi tanulásban és más területeken alkalmazható.

Néhány további előrelépés ezen a vonalon bizonyos, de vannak korlátok. 2015-ben Le Gall és két munkatársa bizonyított hogy a jelenlegi megközelítés – a lézeres módszer a Coppersmith-Winograd receptúrával párosulva – nem tud 2.3078 alatti omegát adni. Le Gall azt mondta, hogy további fejlesztésekhez javítani kell Coppersmith és Winograd eredeti [megközelítésén], amely 1987 óta nem igazán változott. " De eddig senki nem talált ki jobbat. Lehet, hogy nem is lesz.

"Az omega javítása valójában a probléma megértésének része" - mondta Zhou. „Ha jól megértjük a problémát, akkor jobb algoritmusokat tervezhetünk rá. [És] az emberek még mindig nagyon korai szakaszában vannak annak, hogy megértsék ezt az ősi problémát.”