„Megfelelő” eltolási szabályok a zavart paraméteres kvantumevolúciók származékaihoz

„Megfelelő” eltolási szabályok a zavart paraméteres kvantumevolúciók származékaihoz

Időbélyeg: 11. július 2023. 5:48

Dirk Oliver Theis

Elméleti számítástechnika, Tartui Egyetem, Észtország

Érdekesnek találja ezt a cikket, vagy szeretne megvitatni? Scite vagy hagyjon megjegyzést a SciRate-en.

Absztrakt

Banchi és Crooks (Quantum, 2021) módszereket adott a várható értékek deriváltjainak becslésére egy olyan paraméter függvényében, amely a $xmapsto e^{i(x A + B)/hbar}$ „megzavart” kvantumevolúción keresztül lép be. Módszereik módosításokat igényelnek a pusztán paraméterek megváltoztatásán túl a megjelenő egységeken. Ráadásul abban az esetben, ha a $B$-tag elkerülhetetlen, úgy tűnik, hogy a derivált pontos módszere (elfogulatlan becslése) nem ismert: Banchi & Crooks módszere közelítést ad.
Ebben a cikkben az ilyen típusú paraméterezett várható értékek deriváltjainak becslésére egy olyan módszert mutatunk be, amely csak paraméterek eltolását igényli, a kvantumevolúciók egyéb módosításait nem ("megfelelő" eltolási szabály). Módszerünk egzakt (azaz analitikus származékokat, elfogulatlan becsléseket ad), és ugyanaz a legrosszabb eset varianciája, mint a Banchi-Crooks-féle.
Ezen túlmenően megvitatjuk a megfelelő eltolási szabályokat körülvevő elméletet, amely a zavart paraméteres kvantumevolúciók Fourier-analízisén alapul, ami a megfelelő eltolási szabályok Fourier-transzformációi alapján történő jellemzését eredményezi, ami viszont a megfelelő nemlétezési eredményekhez vezet. váltási szabályok a műszakok exponenciális koncentrációjával. Levezetünk olyan csonka módszereket, amelyek közelítési hibákat mutatnak, és összehasonlítjuk Banchi-Crooks módszereivel, előzetes numerikus szimulációk alapján.

“Proper” Shift Rules for Derivatives of Perturbed-Parametric Quantum Evolutions PlatoBlockchain Data Intelligence. Vertical Search. Ai.

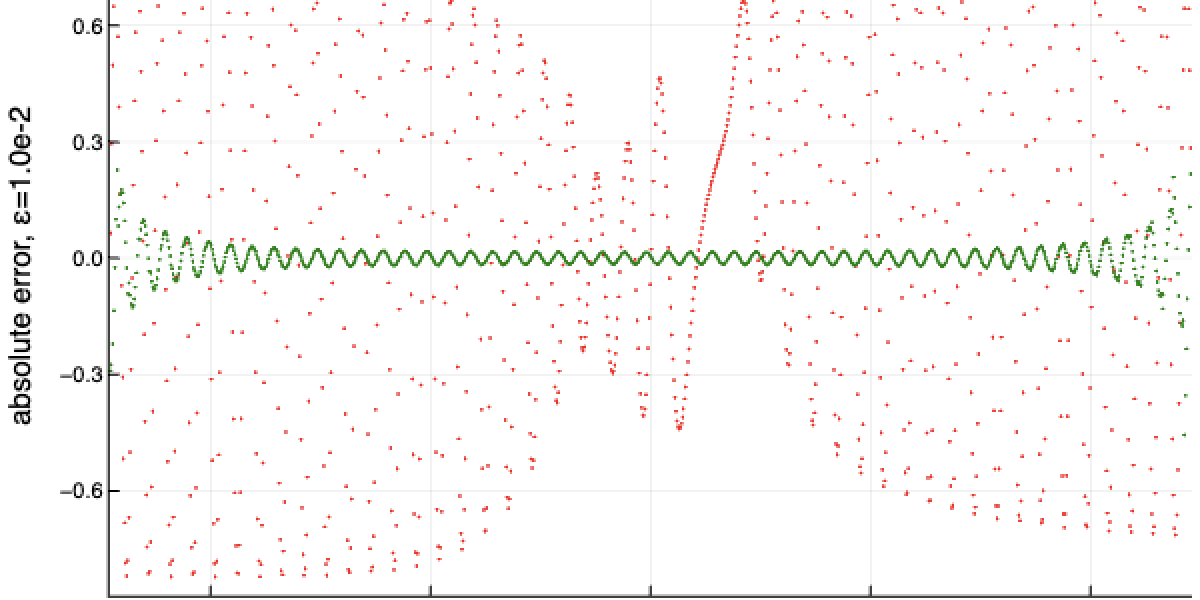
Kiemelt kép: Az előzetes számszerű eredmények azt mutatják, hogy az új módszer jobb, mint a legkorszerűbb. Itt van egy diagram, amely egy véletlenszerűen kiválasztott paraméterezett kvantumevolúció esetén mutatja a függőlegesen a deriváltak becslésének hibáját (elfogultságát), a vízszintesen pedig a paraméterértéket. A zöld pontok az új módszer hibáját mutatják, a piros pontok a technika korszerűségét adják. (A többi teljesítményváltozó mindkét módszernél rögzített és egyenlő.)

Népszerű összefoglaló

A jelenkori vagy a közeljövő kvantumeszközeinek értelmes számításokhoz való felhasználására tett kísérletek során széles körben alkalmazzák a variációs hibrid kvantum-klasszikus megközelítést. Ez abból áll, hogy paraméterezzük a kvantumevolúciót, majd ezeket a paramétereket ciklusban optimalizáljuk, váltakozva a kvantum és a klasszikus számítások között.

Egy másik megközelítés abban áll, hogy egy számítási problémát leképeznek egy Hamilton-rendszerre, amely kvantumhardveren megvalósítható. Például a Maximum Stable Set probléma modellezéséhez hidegatomos kvantumeszközökön a Rydberg-blokád módot jelenthet a stabilitási korlátok részleges megvalósítására.

Természetesen folynak kísérletek a két megközelítés kombinálására.

A paraméterek optimalizálására a variációs megközelítés jellemzően a gradiens becslőit alkalmazza, és ezeknek a becsléseknek kis torzítással és kis szórással kell rendelkezniük. A digitális kvantumszámítási világban – azaz a (paraméterezett) kapukapukat tartalmazó kvantumáramkörökben – a gradiensek becslése jól érthető, és az ún. 𝑙𝑒𝑠. De a digitális és analóg kombinálásakor az a helyzet áll elő, hogy a Hamilton-paraméterezett része nem ingázik más részekkel.
Gondoljon arra, hogy a Rabi-frekvenciát választja a paraméterek között, mondjuk lokálisan egyetlen atomra, Rydberg-atomok tömbjében: A Rabi-kifejezés nem ingázik a Rydberg-blokád kifejezésekkel. Még sok példa létezik. Ezekben a helyzetekben az ismert shift-rule elmélet megbomlik.
Cikkünkben egy új módszert javasolunk a deriváltak becslésére ezekre a helyzetekre. Módszerünk az ismert shift-rule paradigma mentén működik, és javítja a technika állását a becslő torzításának csökkentésében.

► BibTeX adatok

► Referenciák

[1] Jarrod R McClean, Nicholas C Rubin, Joonho Lee, Matthew P Harrigan, Thomas E O'Brien, Ryan Babbush, William J Huggins és Hsin-Yuan Huang. „Amit a kvantumszámítástechnika alapjai megtanítanak a kémiáról”. The Journal of Chemical Physics 155, 150901 (2021).
https://​/​doi.org/​10.48550/​arXiv.2106.03997

[2] Xiao Yuan, Suguru Endo, Qi Zhao, Ying Li és Simon C Benjamin. „A variációs kvantumszimuláció elmélete”. Quantum 3, 191 (2019).
https://​/​doi.org/​10.48550/​arXiv.1812.08767

[3] Kosuke Mitarai, Makoto Negoro, Masahiro Kitagawa és Keisuke Fujii. „Kvantumkör tanulás”. Phys. Rev. A 98, 032309 (2018).
https://​/​doi.org/​10.1103/​PhysRevA.98.032309

[4] Marcello Benedetti, Erika Lloyd, Stefan Sack és Mattia Fiorentini. „Paraméterezett kvantumáramkörök, mint gépi tanulási modellek”. Quantum Science and Technology 4, 043001 (2019).
https:/​/​doi.org/​10.1088/​2058-9565/​ab4eb5

[5] Edward Farhi, Jeffrey Goldstone és Sam Gutmann. „A kvantumközelítő optimalizálási algoritmus”. Preprint (2014).
https://​/​doi.org/​10.48550/​arXiv.1411.4028

[6] Eric R Anschuetz, Jonathan P Olson, Alán Aspuru-Guzik és Yudong Cao. „Variációs kvantumfaktoring”. Nyomtatás előtt (2018).
https://​/​doi.org/​10.48550/​arXiv.1808.08927

[7] Carlos Bravo-Prieto, Ryan LaRose, Marco Cerezo, Yigit Subasi, Lukasz Cincio és Patrick J Coles. „Variációs kvantumlineáris megoldó”. Nyomtatás előtt (2019).
https://​/​doi.org/​10.48550/​arXiv.1909.05820

[8] Ryan Babbush és Hartmut Neven. „Kvantumevolúciók képzése szublogikus vezérlők segítségével” (2019). US 10,275,717 számú szabadalom.

[9] Louis-Paul Henry, Slimane Thabet, Constantin Dalyac és Loïc Henriet. „Kvantum evolúciós kernel: Gépi tanulás grafikonokon programozható qubit tömbökkel”. Fizikai Szemle A 104, 032416 (2021).
https://​/​doi.org/​10.48550/​arXiv.2107.03247

[10] Constantin Dalyac, Loïc Henriet, Emmanuel Jeandel, Wolfgang Lechner, Simon Perdrix, Marc Porcheron és Margarita Veshcezerova. „Minősítő kvantummegközelítések kemény ipari optimalizálási problémákhoz. esettanulmány az elektromos járművek intelligens töltésével kapcsolatban”. EPJ Quantum Technology 8, 12 (2021).
https://​/​doi.org/​10.48550/​arXiv.2012.14859

[11] Ryan Sweke, Frederik Wilde, Johannes Meyer, Maria Schuld, Paul K Fährmann, Barthélémy Meynard-Piganeau és Jens Eisert. „Sztochasztikus gradiens süllyedés hibrid kvantum-klasszikus optimalizáláshoz”. Quantum 4, 314 (2020).
https://​/​doi.org/​10.48550/​arXiv.1910.01155

[12] Jun Li, Xiaodong Yang, Xinhua Peng és Chang-Pu Sun. „Hibrid kvantum-klasszikus megközelítés a kvantumoptimális szabályozáshoz”. Phys. Rev. Lett. 118, 150503 (2017).
https://​/​doi.org/​10.1103/​PhysRevLett.118.150503

[13] Leonardo Banchi és Gavin E. Crooks. „Az általános kvantumevolúció analitikus gradienseinek mérése a sztochasztikus paramétereltolási szabállyal”. Quantum 5, 386 (2021).
https:/​/​doi.org/​10.22331/​q-2021-01-25-386

[14] Richard P Feynman. „Egy operátorszámítás, amelynek kvantumelektrodinamikai alkalmazásai vannak”. Physical Review 84, 108 (1951).
https://​/​doi.org/​10.1103/​PhysRev.84.108

[15] Ralph M Wilcox. „Exponenciális operátorok és paraméterdifferenciálás a kvantumfizikában”. Journal of Mathematical Physics 8, 962–982 (1967).
https://​/​doi.org/​10.1063/​1.1705306

[16] Javier Gil Vidal és Dirk Oliver Theis. „Számítás paraméterezett kvantumáramkörökön”. Nyomtatás előtt (2018).
https://​/​doi.org/​10.48550/​arXiv.1812.06323

[17] David Wierichs, Josh Izaac, Cody Wang és Cedric Yen-Yu Lin. „Általános paramétereltolási szabályok kvantumgradiensekhez”. Nyomtatás előtt (2021).
https://​/​doi.org/​10.48550/​arXiv.2107.12390

[18] Dirk Oliver Theis. „Véges támaszú paramétereltolási szabályok optimalitása variációs kvantumáramkörök származékaihoz”. Nyomtatás előtt (2021).
https://​/​doi.org/​10.48550/​arXiv.2112.14669

[19] Michael Reed és Barry Simon. „A modern matematikai fizika módszerei II: Fourier-analízis, önadjunktálás”. 2. kötet. Akadémiai Kiadó. (1975).

[20] Jarrod R McClean, Sergio Boixo, Vadim N Smelyanskiy, Ryan Babbush és Hartmut Neven. „Kivár fennsíkok kvantum-neurális hálózatok képzési tájain”. Nature Communications 9, 4812 (2018).
https:/​/​doi.org/​10.1038/​s41467-018-07090-4

[21] Andrew Arrasmith, Zoë Holmes, Marco Cerezo és Patrick J Coles. „A kvantum-kietlen fennsíkok egyenértékűsége a költségkoncentrációval és a szűk szurdokokkal”. Quantum Science and Technology 7, 045015 (2022).
https://​/​doi.org/​10.48550/​arXiv.2104.05868

[22] Walter Rudin. „Funkcionális elemzés”. McGraw-Hill. (1991).

[23] Elias M Stein és Rami Shakarchi. „Fourier-analízis: Bevezetés”. 1. kötet Princeton University Press. (2011).

[24] Gerald B Folland. „Absztrakt harmonikus elemzés tanfolyam”. 29. kötet. CRC sajtó. (2016).

[25] Don Zagier. „A dilogaritmusfüggvény”. A határok számelméletben, fizikában és geometriában II. 3–65. oldal. Springer (2007).

[26] Leonard C Maximon. „A komplex argumentum dilogaritmusfüggvénye”. A Londoni Királyi Társaság közleménye. A sorozat: Mathematical, Physical and Engineering Sciences 459, 2807–2819 (2003).
https://​/​doi.org/​10.1098/​rspa.2003.1156

[27] Elias M Stein és Rami Shakarchi. „Komplex elemzés”. 2. kötet. Princeton University Press. (2010).

[28] Walter Rudin. „Valós és összetett elemzés”. McGraw-Hill. (1987).

[29] Heinz Bauer. „Maß- und Integrationstheorie”. Walter de Gruyter. (1992). 2. kiadás.

[30] Franz Relich és Joseph Berkowitz. „Sajátérték-problémák perturbációelmélete”. CRC Press. (1969).

Idézi

[1] Roeland Wiersema, Dylan Lewis, David Wierichs, Juan Carrasquilla és Nathan Killoran: „Itt jön a $mathrm{SU}(N)$: többváltozós kvantumkapuk és gradiensek”, arXiv: 2303.11355, (2023).

A fenti idézetek innen származnak SAO/NASA HIRDETÉSEK (utolsó sikeres frissítés: 2023-07-14 10:03:06). Előfordulhat, hogy a lista hiányos, mivel nem minden kiadó ad megfelelő és teljes hivatkozási adatokat.

On Crossref által idézett szolgáltatás művekre hivatkozó adat nem található (utolsó próbálkozás 2023-07-14 10:03:04).

Ez a tanulmány a Quantumban jelent meg Creative Commons Nevezd meg 4.0 International (CC BY 4.0) engedély. A szerzői jog az eredeti szerzői jog tulajdonosainál marad, például a szerzőknél vagy intézményeiknél.

Időbélyeg:

Még több Quantum Journal