A legnagyobb legkisebb háromszög éppen kisebb lett | Quanta Magazin

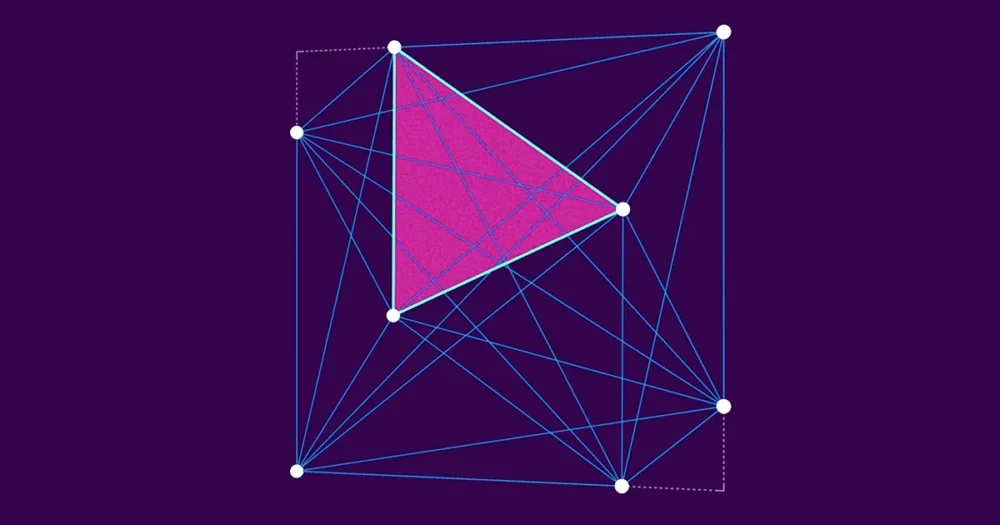
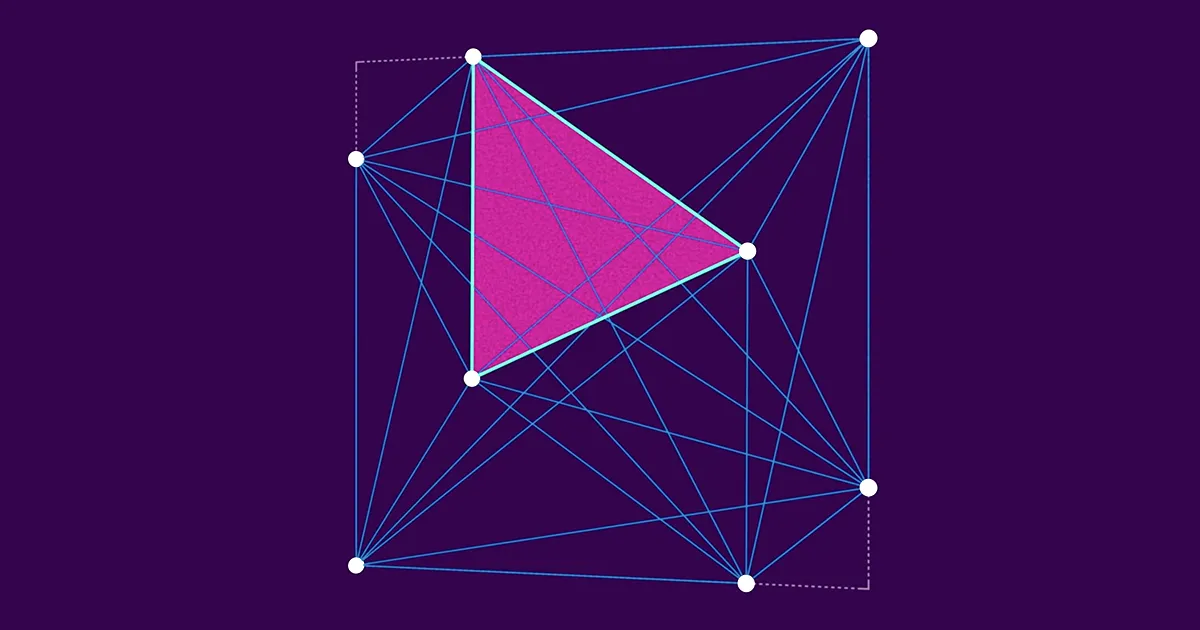
Tekintsünk egy négyzetet, amelyben egy csomó pont található. Vegyünk három pontot ebből a pontból, és készítsünk egy háromszöget. Négy pont négy különböző háromszöget határoz meg. Tíz pont 120 háromszöget határoz meg. A számok innentől gyorsan nőnek – 100 pont 161,700 XNUMX különböző háromszöget határoz meg. Természetesen minden háromszögnek van egy területe.

Hans Heilbronn német matematikus, aki a második világháború előtt elmenekült hazájából, és Angliában telepedett le, ezekre a háromszögekre gondolt az 1940-es évek végén, amikor egy csapat katonát látott az ablaka előtt. Úgy tűnt, hogy a katonák nem voltak formációban, ezért arra gondolt: Ha vannak n katonák egy négyzetben, mekkora a három által meghatározott lehető legnagyobb legkisebb háromszög? Heilbronn azon töprengett, hogyan lehetne elrendezni a katonákat (vagy a matematikai egyszerűség kedvéért a pontokat), hogy maximalizálja a legkisebb háromszög méretét.

A probléma megfogalmazása egyszerű, de a Heilbronn-háromszög-probléma, ahogyan ezt nevezték, fejlődése megtorpant, és az eredmények az 1980-as években teljesen kiszáradtak. Aztán tavaly májusban három matematikus Alex Cohen, Cosmin Pohoata és a Dmitrij Zakharov – jelentette be a új sapka a legkisebb háromszög méretén. „Szerintem ez egy lenyűgöző eredmény” – mondta Anthony Carbery, az Edinburghi Egyetem matematikusa.

A kutatók az évek során folyamatosan dolgoztak a Heilbronn-háromszög problémán, annak ellenére, hogy hosszasan kellett várni a haladásra, amit a matematika más területeihez fűződő kapcsolatok szövevénye motivált. "A dolgok, amelyekhez kapcsolódik, hogy életre keltsék" - mondta Pohoata, az atlantai Emory Egyetem professzora. Ez szorosan kapcsolódik a metsző alakzatokkal kapcsolatos problémákhoz, amelyek viszont mind a számelmélethez, mind a Fourier-analízishez kapcsolódnak – az egyszerű hullámokból felépített bonyolult függvények tanulmányozásához.

Cohen, a Massachusetts Institute of Technology végzős hallgatója tavaly bukkant rá a kapcsolatok hálójára. Egy régi felmérést olvasott a Heilbronn-háromszög problémájáról, Klaus Rothtól, egy másik nácik elől menekülttől, aki kisfiúként Nagy-Britanniába menekült. (Roth, aki 2015-ben halt meg, volt az első brit matematikus, aki elnyerte a Fields-érmet.)

Cohen egy egyszerű képpel jelenítette meg Roth felméréséből származó ötleteket: egy négyzet, amelyet két vastag csík keresztez, és mindegyik közepén vékony vonallal. Miközben tanulmányozta a diagramját, Cohen rájött, hogy ez kapcsolódhat olyan gondolatokhoz, amelyeket tanácsadója, Larry Guth felvetett egy nemrégiben tartott olvasócsoport-találkozón. De Guth egyáltalán nem beszélt a háromszögekről.

"Nagyon gyorsan rájöttem, hogy ez a két módszer lényegében egyenértékű" - mondta Cohen. "Nagyon izgatott lettem a háromszög probléma miatt."

Egy nap az MIT matematikai tanszékének közös helyiségében Cohen váratlanul felfedezte, hogy Pohoata, aki előadást tartott, és Zakharov, az MIT végzős diáktársa szintén a Heilbronn-háromszög problémán dolgozott. Mi több, ugyanazt a linket találták. Mindhárman elkezdtek együttműködni. Hét hónappal később megtörtént az áttörés. Dolgozatuk a matematika még több új területét hozza magával. „Óriási mennyiségű gépet és különféle betekintést használnak” – mondta Thomas Bloom, az Oxfordi Egyetem munkatársa, aki azt várja, hogy az új tanulmány „reneszánszát” indítja el a háromszög-probléma terén.

Megdőlt egy hipotézis

Ha három pontot nagyon közel helyezünk egymáshoz, könnyen tetszőlegesen kicsinyíthetjük az elrendezés legkisebb háromszögét. (A legszélsőségesebb esetben három egymással egy vonalban lévő pont nulla területű háromszöget alkot.) De a legkisebb háromszöget is bonyolultabb megpróbálni nagynak tartani. Ahogy egyre több pontot ad hozzá, a legkisebb háromszög kénytelen nagyon kicsinek lenni – az új pontok csak olyan távol lehetnek a meglévőktől. Viszonylag könnyű megmutatni, hogy a legkisebb háromszög területe nem lehet nagyobb 1/(n − 2) úgy, hogy a négyzetet nem átfedő háromszögekre bontjuk.

De Heilbronn úgy gondolta, hogy a határ még ennél is kisebb. Úgy sejtette, hogy bárhogyan is helyezkednek el a pontok a négyzetben, nem létezhet olyan legkisebb háromszög, amelynek területe nagyobb, mint 1/n², egy szám, amely sokkal gyorsabban zsugorodik, mint n növekszik.

Tévedett.

1980-ban a magyar matematikusok Komlós János, Pintz János és Szemerédi Endre talált egy mintát pontok, amelyek legkisebb háromszögének területe valamivel nagyobb, mint 1/n². Egy körülbelül ugyanebben az időben megjelent külön cikkben azt is megmutatták, hogy lehetetlen elintézni n pontokat egy legkisebb háromszög létrehozásához, amely nagyobb, mint körülbelül 1/n^8/7. Amikor n nagy, ez sokkal kisebb, mint 1/n, de sokkal nagyobb, mint 1/n².

Ezek az eredmények több mint 40 évig megmaradtak. „A [a kötöttség] javítása mindkét irányban rendkívül nehéz volt, és sok technikai elemzést és találékonyságot igényelt” – mondta Bloom.

„Nagyon-nagyon hamar elakadsz a dolgok teljes mocsarában” – tette hozzá Carbery.

Míg az 1980-ban felfedezett építmény továbbra is a legnagyobb ismert legkisebb háromszöggel rendelkezik, Cohennek, Pohoatának és Zakharovnak négy évtized után először sikerült csökkentenie a felső határt.

Konvergens evolúció

Mire Cohennel találkozott, Pohoata már két éve dolgozott a Heilbronn-háromszög problémáján. 2020 nyarán a Yale Egyetem nyári kutatóhallgatóit arra bíztatta, hogy a probléma magasabb dimenziós változatain dolgozzanak – például szűkítsék a háromdimenziós kockában szétszórt pontok között megjelenő legnagyobb, legkisebb térfogatú alakzatokat.

A projekt részeként Pohoata felülvizsgálta a problémával kapcsolatos összes korábbi munkát. Vissza az 1951-ban, Roth két részre osztotta a kis háromszögek keresését: Először keressen egy pontpárt a háromszög alapjának kialakításához, majd keressen egy harmadik pontot a háromszög befejezéséhez. A stratégia lényegében a legnagyobb, legkisebb háromszög keresését az egymást metsző pontok és téglalapok tanulmányozásaként fogalmazta meg – ezt a megközelítést Wolfgang Schmidt finomította 1972-ben.

Schmidt írása olvasásakor Pohoata összefüggést azonosított a magas-alacsony módszerrel – ezzel a technikával, amelyet Guth és munkatársai 2017-ben fejlesztettek ki a téglalap alakú csíkok és a lemezek gyűjteménye közötti átfedés becslésére. „Ez egy fontos pszichológiai pillanat volt számomra” – mondta.

2021-ben Pohoata felhozta elképzeléseit Zakharovval. Ők ketten akkor kezdtek el közösen publikálni, amikor Zaharov még egyetemista volt Moszkvában. „[Zaharov] figyelemre méltó dolgokat művelt, mintha fiatalon vezető kutató lett volna” – mondta Jacob Fox, a Stanford Egyetem matematikusa.

Zaharov kezdetben pesszimista volt a Heilbronn-háromszög problémájával kapcsolatban. „Azt hittem, ez a 8/7 ott maradt 40 évig, szóval ki vagyok én, hogy feltörjem?” ő mondta. – Leginkább azt szerettem volna megérteni, hogyan működik.

Miután 2022 októberében összefutottak, Cohen, Pohoata és Zaharov hamar rávilágítottak arra az akadályra, amellyel Komlós, Pintz és Szemerédi tudtukon kívül szembesültek. "Van egy nagyon konkrét elrendezése a pontoknak, ami ehhez a legrosszabb forgatókönyvhöz vezet, ahol nem tudnak jobban teljesíteni, mint 8/7" - mondta Cohen. „A pontokat lehet koncentrálni vagy szétszórni. A legrosszabb eset az, ha valamilyen kombinációról van szó.” Ennek az elrendezésnek a pontjai nagy léptékben oszlanak el, de ha az egységnégyzeten belüli apró résznégyzetekre nagyít, rendezett mintákat láthat.

Cohen, Pohoata és Zakharov rájöttek, hogy a kis pontcsoportok dimenziójának tanulmányozásával előreléphetnek. A nem matematikusok számára a méretek mindig egész számok: Egy papírlap kétdimenziós; egy agyagtégla háromdimenziós.

A dolgok furcsává válhatnak, ha figyelembe vesszük egy ponthalmaz dimenzióját. Egyetlen pontot általában nulldimenziósnak tekintünk. De két véges ponthalmaznak teljesen eltérő szerkezete lehet. Lehet, hogy az egyiknek 10 pontja engedelmesen masíroz egy rúd-egyenesben, míg a másiknak 10 pontja van elszórva a teljes egységmezőn.

A 20. század eleji matematikus, Felix Hausdorff a dimenzió új fogalmával állt elő, hogy a legfurcsább ponthalmazok szerkezetét is megragadja. E meghatározás szerint egy egyenes 10 pontja egydimenziós, míg a négyzeten egyenletesen elosztott 10 pont kétdimenziós. De ebben a világban a dimenzióknak nem kell egész számoknak lenniük, és egy egydimenziós halmaz nem lineáris, hanem fraktál, bonyolult minták végtelen rétegeit sportolhatja. A minták részleteitől függően a pontgyűjtemények mérete akár 0-nál nagyobb, de 1-nél kisebb is lehet.

Cohen, Pohoata és Zakharov feltárt egy 1953 tétel John Marstrand, amely átfogalmazta Komlós, Pintz és Szemerédi becslését a Hausdorff-dimenzió szempontjából – de csak 1-nél nagyobb dimenziókra. A becslés javítása érdekében Cohennek, Pohoatának és Zakharovnak valamilyen módot kell találnia arra, hogy Marstrand eredményét halmazokra általánosítsák. amelynek mérete kisebb volt 1-nél.

Kapcsolatok létrehozása

Cohennek, Pohoatának és Zaharovnak nem kellett sokáig gondolkodniuk. Ahogy történt, egy újság Tuomas Orponen, Pablo Shmerkin és a Hong Wang az éppen volt online közzétett kiterjesztette Marstrand 70 éves tételét olyan halmazokra, amelyek mérete kisebb volt 1-nél.

Cohen csak februárban szerzett tudomást a lapról. Miután megtette, gyorsan továbbította Pohoatának és Zaharovnak. Május végére feltették az újságukat az internetre, bizonyítva, hogy a legkisebb háromszög közöttük n Az egységnégyzet pontjai soha nem lehetnek nagyobbak 1-nél/n^{8 / 7 + 1 / 2000}.

Shmerkin egy szeszélyből olvasta a háromszög papírt, miután meglátta, hogy a Twitteren bejelentették. Azelőtt nem is volt tisztában a Heilbronn-háromszög problémájával, ezért meglepődött, amikor észrevette a bizonyítékára való hivatkozást. „Ez nem közvetlen alkalmazása annak, amit csinálunk. Sok éleslátó, kreatív és technikai munka van benne” – mondta. – Számomra ez nagyszerű érzés volt.

Bloom is le volt nyűgözve. "Sokáig nézhettem volna azt a papírt, és soha nem gondoltam volna, hogy ez a háromszög problémára vonatkozik."

Míg az új eredmény csak töredékével javítja Komlós, Pintz és Szemerédi kitevőjét, újjáélesztette a régóta lappangó Heilbronn-háromszög problémát. „Előfordulhat, hogy egy pillantást vethetsz rá, és azt mondod: ásíts, ásíts, ásíts, nem tűnik annyira másnak, mint ami 1982-ben ismert volt. De rettenetesen sok idő telt el 1982 óta” – mondta Carbery.

A magas-alacsony módszer és Orponen, Shmerkin és Wang munkájának beépítésével Cohen, Pohoata és Zakharov új kapcsolatokat tártak fel a Heilbronn-háromszög probléma és a matematika többi része között. Ahogy Bloom fogalmazott, a háromszög-problémát úgy gondolták, mint „egy igazán szép, nagyon nehéz problémát, amivel nem tudjuk, mit tegyünk. De azt mondták, hogy ez rengeteg más dologhoz kapcsolódik.”

Egyesek úgy vélik, hogy a Heilbronn-féle háromszög-problémára adott igaz válasz nem lesz sokkal nagyobb, mint az eredeti sejtése 1/n². „Ha strukturáltan teszek fel pontokat, kudarcot vallok; ha véletlenszerűen teszek fel pontokat, akkor kudarcot vallok. Nem lehet túl strukturált, nem lehet túl véletlenszerű, ezért valószínűleg nem is létezik” – mondta Bloom. Zaharov azonban más válaszban reménykedik. Az intuíciók, amelyek alátámasztják az 1/n² „Kicsit unalmasak” – mondta. „Sokkal jobban szeretném, ha így lenne n^3/2. "