A Dirichlet-folyamat keverék modellje

• Június 23, 2014
• Vasilis Vryniotis
• . 2 megjegyzés

Ez a blogbejegyzés a sorozat negyedik része Klaszterezés Dirichlet folyamatkeverék modellekkel. Korábbi cikkeinkben tárgyaltuk a véges Dirichlet keverékmodelleket, és felvettük a modelljük határait végtelen k klaszterekre, ami elvezetett minket a Dirichlet-folyamatok bevezetéséhez. Amint láttuk, a célunk egy olyan keverékmodell felépítése, amelyhez nem kell kezdettől fogva megadnunk k klaszter/összetevő számát. Után a Dirichlet-folyamatok különböző reprezentációinak bemutatása, itt az ideje, hogy ténylegesen használjuk a DP-ket egy végtelen keverékmodell felépítésére, amely lehetővé teszi számunkra, hogy klaszterezést hajtsunk végre. Ennek a cikknek a célja a Dirichlet-folyamat-keverék modellek meghatározása, valamint a kínai éttermi folyamat és a Gibbs-mintavétel használatának megvitatása. Ha még nem olvastad a korábbi bejegyzéseket, erősen ajánlott ezt megtenni, mivel a téma kissé elméleti jellegű, és a modell felépítésének alapos megértését igényli.

Frissítés: A Datumbox Machine Learning Framework nyílt forráskódú és ingyenes letöltés. Tekintse meg a com.datumbox.framework.machinelearning.clustering csomagot a Dirichlet Process Mixture Models Java-ban való megvalósításának megtekintéséhez.

1. A Dirichlet-folyamat keverékmodell definíciója

A Dirichlet-folyamatok használata lehetővé teszi, hogy végtelen komponensekből álló keverékmodellt hozzunk létre, amely úgy képzelhető el, hogy a k véges modelljének határát a végtelenbe viszi. Tegyük fel, hogy a következő modellünk van:

1. egyenlet: Dirichlet-eljárási keverékmodell

Ahol G a következőképpen van definiálva és a rövid jelöléseként használják ami egy delta függvény, amely 1 if-t vesz fel és 0 máshol. A θ_i a G-ből mintavételezett klaszterparaméterek. Az F generatív eloszlást a θ klaszterparaméterek konfigurálják_i és x generálására szolgál_i megfigyelések. Végül meghatározhatunk egy sűrűségeloszlást ami a mi keverékeloszlásunk (számlálható végtelen keverék) keverési arányokkal és komponensek keverése .

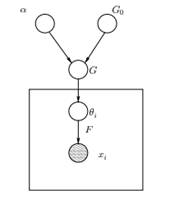
1. ábra: Dirichlet-folyamat-keverék modell grafikus modellje

Fent láthatjuk a DPMM megfelelő grafikus modelljét. A G₀ a DP alapeloszlása, és általában az F generatív eloszlás előtt konjugálásra kerül, hogy megkönnyítsük a számításokat és kihasználjuk a vonzó matematikai tulajdonságokat. Az α a Dirichlet-folyamat skaláris hiperparamétere, és befolyásolja a kapott klaszterek számát. Minél nagyobb az α értéke, annál több a klaszter; minél kisebb az α, annál kevesebb a klaszter. Meg kell jegyeznünk, hogy α értéke kifejezi a hit ereje a G₀. A nagy érték azt jelzi, hogy a legtöbb minta különálló lesz, és értékeik a G-re koncentrálódnak₀. A G a DP-ből mintavételezett véletlenszerű eloszlás a Θ paramétertérben, amely valószínűségeket rendel a paraméterekhez. A θ_i egy paramétervektor, amely a G eloszlásból származik és tartalmazza a klaszter paramétereit, az F eloszlást θ paraméterezi_i és x_i az F generatív eloszlás által generált adatpont.

Fontos megjegyezni, hogy a θ_i a Θ paramétertér elemei, és „konfigurálják” a klasztereinket. Látens változóknak is tekinthetők x-en_i amelyek megmondják, hogy melyik komponensből/klaszterből származik az x_i honnan származik, és melyek ennek a komponensnek a paraméterei. Így minden x-re_i hogy megfigyeljük, rajzolunk egy θ-t_i a G eloszlásból. Minden sorsolásnál az eloszlás az előző kijelölések függvényében változik. Ahogy a Blackwell-MacQueen urna sémában láttuk, a G-eloszlás integrálható, és a jövőbeni θ-választásaink_i csak G-n múlik₀: . A θi paraméterek becslése az előző képletből nem mindig kivitelezhető, mivel sok megvalósítás (például a kínai étterem folyamata) magában foglalja a exponenciálisan növekvő k komponens. Így közelítő számítási módszereket használnak, például Gibbs-mintavételt. Végül meg kell jegyeznünk, hogy bár a k klaszter végtelen, az aktív klaszterek száma igen . Így a θ_i megismétlődik, és klaszterező hatást fog kifejteni.

2. Végtelen keverékmodell definiálása a kínai étterem eljárással

Az előző szegmensben definiált modell matematikailag szilárd, de van egy nagy hátránya: minden új x_i amit megfigyelünk, új θ-t kell mintát vennünk_i figyelembe véve a θ korábbi értékeit. A probléma az, hogy sok esetben ezeknek a paramétereknek a mintavételezése nehéz és számításigényes feladat lehet.

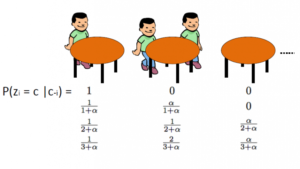
Alternatív megoldás a kínai étterem folyamat használata a z látens változók modellezésére_i a klaszter-hozzárendelésekből. Így a θ használata helyett_i a klaszterparaméterek és a klaszter-hozzárendelések jelölésére a z látens változót használjuk._i a fürtazonosító jelzésére, majd ezzel az értékkel rendelheti hozzá a fürt paramétereit. Ennek eredményeként többé nem kell mintát venni egy θ-ből minden alkalommal, amikor új megfigyelést kapunk, hanem a z mintavételével kapjuk meg a klaszter hozzárendelést_i a CRP-ből. Ezzel a sémával egy új θ csak akkor kerül mintavételre, ha új klasztert kell létrehoznunk. Az alábbiakban bemutatjuk ennek a megközelítésnek a modelljét:

2. egyenlet: Keverékmodell CRP-vel

A fenti egy generatív modell, amely leírja, hogyan az adatok x_i és létrejönnek a klaszterek. A klaszteranalízis elvégzéséhez az x megfigyeléseket kell használnunk_i és becsüljük meg a z klaszter hozzárendeléseket_i.

3. Mixture Model Inference és Gibbs-mintavétel

Sajnos mivel a Dirichlet-folyamatok nem paraméteresek, mi nem tudja használni az EM algoritmust a fürt-hozzárendeléseket tároló látens változók becslésére. A feladatok becsléséhez a Összecsukott Gibbs-mintavétel.

A Collapsed Gibbs Sampling egy egyszerű Markov Chain Monte Carlo (MCMC) algoritmus. Gyors, és lehetővé teszi számunkra, hogy egyes változókat integráljunk, miközben egy másik változót mintavételezünk. Ennek ellenére ehhez az algoritmushoz ki kell választanunk egy G-t₀ amely az F generatív eloszlás konjugált priorja annak érdekében, hogy analitikusan meg lehessen oldani az egyenleteket, és közvetlenül tudjon mintát venni .

Az összecsukott Gibbs-mintavétel lépései, amelyeket a klaszter-hozzárendelések becsléséhez használunk, a következők:

• Inicializálja a z-t_i a klaszter-hozzárendeléseket véletlenszerűen
• Ismételje meg a konvergencia eléréséig
• Válassza ki véletlenszerűen ax_i
  
• Tartsa meg a másik z_j minden j≠i-hez rögzítve:
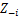
• Rendeljen új értéket z-hez_i a z-től függő „CRP valószínűség” kiszámításával_j és x_j az összes j≠i közül:

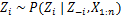
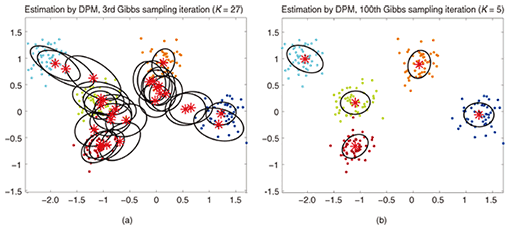
A következő cikkben arra fogunk összpontosítani, hogyan végezzünk klaszterelemzést Dirichlet Process Mixture modellek használatával. Két különböző Dirichlet-folyamat-keverékmodellt fogunk meghatározni, amelyek a kínai éttermi folyamatot és az összecsukott Gibbs-mintavételt használják a folyamatos adatkészletek és dokumentumok klaszterezésének végrehajtására.