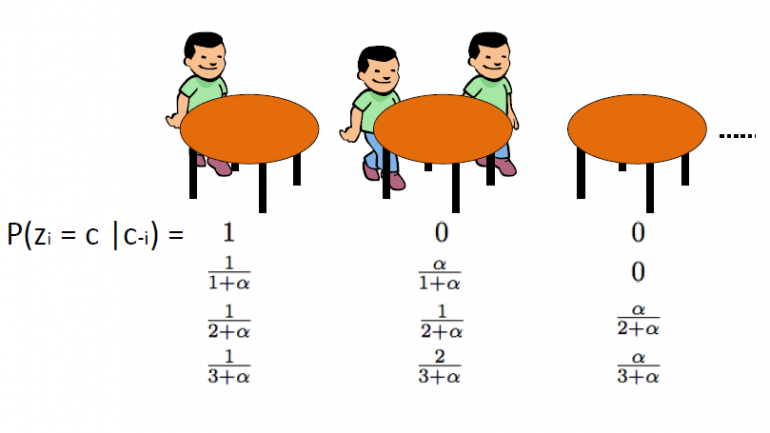A Dirichlet-folyamat a kínai éttermi folyamat és egyéb ábrázolások

• May 20, 2014
• Vasilis Vryniotis
• . Nincs hozzászólás

Ez a cikk a klaszterezés Dirichlet-folyamatkeverék-modellekkel című sorozatának harmadik része. Az előző alkalommal a Dirichlet-eloszláson alapuló véges keverék modellt definiáltuk, és kérdéseket tettünk fel arra vonatkozóan, hogyan tehetjük ezt a modellt végtelenné. Röviden megtárgyaltuk a modell határértékét, amikor a klaszterek k száma a végtelenbe hajlik, de mint hangsúlyoztuk, egy ilyen objektum létezése nem triviális (más szóval, hogyan vegyük valójában egy modell határát ”?). Emlékeztetőül: azért akarjuk a make k-t végtelennek venni, mert így egy nem paraméteres modellt kapunk, amely nem igényli az adatokon belüli klaszterek teljes számának előre definiálását.

Frissítés: A Datumbox Machine Learning Framework nyílt forráskódú és ingyenes letöltés. Tekintse meg a com.datumbox.framework.machinelearning.clustering csomagot a Dirichlet Process Mixture Models Java-ban való megvalósításának megtekintéséhez.

Bár célunk egy olyan modell felépítése, amely képes klaszterezést végezni adathalmazokon, előtte meg kell beszélnünk a Dirichlet-folyamatokat. Megadjuk a DP szigorú matematikai definícióit és intuitívabb magyarázatait, és megvitatjuk a folyamat felépítésének módjait. Ezeket a konstrukciókat/ábrázolásokat úgy tekinthetjük, mint a Dirichlet-folyamat „valódi életben” való előfordulását.

Annak ellenére, hogy kutatási beszámolómat igyekeztem úgy adaptálni, hogy ezek a blogbejegyzések könnyebben követhetőek legyenek, mégis fontos a szükséges matematikai eszközök és eloszlások meghatározása, mielőtt belevágnánk a modellek használatába. A Dirichlet-folyamatmodellek aktív kutatás tárgyát képezik, de használatuk előtt meg kell ismerni a statisztikát és a sztochasztikus folyamatokat. Egy másik probléma, hogy amint ebben a cikkben látni fogjuk, a Dirichlet-folyamatok számos módon ábrázolhatók/konstruálhatók. Ennek eredményeként több akadémiai dolgozat teljesen eltérő jelölést/konvenciót használ, és különböző nézőpontokból vizsgálja a problémát. Ebben a bejegyzésben megpróbálom a lehető legegyszerűbben elmagyarázni őket, és ugyanazt a jelölést használom. Remélhetőleg a dolgok világosabbá válnak a két soron következő cikkben, amelyek a Dirichlet-folyamatkeverék-modellek meghatározására és arra összpontosítanak, hogyan lehet ténylegesen használni őket klaszteranalízis végrehajtására.

1. A Dirichlet-folyamat definíciója

A Θ tér feletti Dirichlet-folyamat sztochasztikus folyamat. Ez egy valószínűségi eloszlás a „Θ térbeli valószínűségi eloszlások” és a húzni belőle egy diszkrét eloszlás. Formálisabban a Dirichlet-eloszlás a valószínűségi mértékek közötti eloszlás. A valószínűségi mérték a Θ-től [0,1]-ig terjedő tér részhalmazainak függvénye. G egy DP elosztott véletlen valószínűségi mérőszám, amelyet a következővel jelölünk , ha bármely partícióhoz (A₁,…A_n) a Θ térből megvan az .

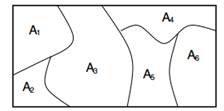
1. ábra: A véges partíciók határértékei Dirichlet eloszlásúak.

A DP-nek két paramétere van: Az első a G alapeloszlás₀ amely úgy szolgál, mint egy átlag . A második az α szilárdsági paraméter, amely szigorúan pozitív és inverz varianciaként szolgál . Meghatározza a kimeneti eloszlás értékei ismétlődésének mértékét. Minél nagyobb a értéke, annál kisebb az ismétlés; minél kisebb az érték, annál nagyobb az output eloszlás értékeinek ismétlődése. Végül a Θ tér az a paramétertér, amelyen a DP-t definiáljuk. Ráadásul a Θ tér egyben G definíciós tere is₀ ami megegyezik G-éval.

Egy egyszerűbb és több intuitív módon a Dirichlet-folyamat magyarázata a következő. Tegyük fel, hogy van egy Θ térünk, amely bármilyen véges módon particionálható (A₁,…,A_n) és egy G valószínűségi eloszlást, amely valószínűségeket rendel hozzájuk. A G egy specifikus valószínűségi eloszlás Θ felett, de sok más is létezik. A Dirichlet-folyamat Θ-n pontosan ezt modellezi; ez egy eloszlás az összes lehetséges valószínűségi eloszláson a Θ téren. A Dirichlet folyamat paraméterezése a G-vel történik₀ bázisfüggvény és az α koncentráció paraméter. Azt mondhatjuk, hogy G DP szerint oszlik el α és G paraméterekkel₀ ha a G által Θ partícióihoz rendelt valószínűségek együttes eloszlása ​​követi a Dirichlet-eloszlást. Alternatív megoldásként azt is mondhatjuk, hogy azok a valószínűségek, amelyeket G Θ bármely véges partíciójához rendel, a Dirichlet-eloszlást követik.

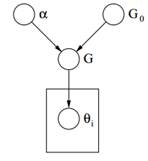
2. ábra: Dirichlet-folyamat grafikus modellje

Végül fent láthatjuk a egy DP grafikus modellje. Meg kell jegyeznünk, hogy α egy skaláris hiperparaméter, G₀ a DP alapeloszlása, G a DP-ből mintavételezett véletlenszerű eloszlás a Θ paramétertérben, amely valószínűségeket rendel a paraméterekhez és θ_i egy paramétervektor, amely a G eloszlásból származik, és a Θ tér eleme.

2. Posterior Dirichlet-folyamatok

A Posterior Dirichlet-folyamatokat tárgyalta Ferguson. Kezdjük azzal, hogy egy Dirichlet-folyamatból rajzolunk egy G véletlenszerű valószínűségi mértéket, . Mivel G egy valószínűségi eloszlás Θ felett, ebből az eloszlásból is mintát vehetünk, és független, azonos eloszlású θ mintákat rajzolhatunk.₁,…, θ_n ~ G. Mivel a Dirichlet-folyamatból származó rajzok diszkrét eloszlások, ábrázolhatjuk ahol egy rövid jelölése ami egy delta függvény, amely 1 if-t vesz fel és 0 máshol. Ennek érdekes hatása, hogy mivel G így van definiálva, pozitív a valószínűsége annak, hogy különböző minták azonos értékűek. . Amint a későbbiekben látni fogjuk, ez egy fürthatást hoz létre, amely felhasználható az adatkészletek fürtelemzésére.

A fenti definíciók és megfigyelések felhasználásával meg akarjuk becsülni a Dirichlet-folyamat posteriorját a θ minták alapján. Ennek ellenére mióta ezt tudjuk és a a Bayes-szabályok és a Dirichlet és a multinomiális konjugácia segítségével azt kapjuk és a .

1. egyenlet: Posterior Dirichlet-folyamat

Ez a tulajdonság nagyon fontos, és a különböző DP-reprezentációk használják.

3. Dirichlet folyamatábrázolások

Az előző szegmensekben meghatároztuk a Dirichlet-folyamatot és bemutattuk annak elméleti modelljét. Az egyik fontos kérdés, amire meg kell válaszolnunk, hogy honnan tudhatjuk, hogy létezik ilyen objektum, és hogyan tehetjük meg konstruálni és reprezentálni egy Dirichlet-eljárás.

A létezés első jeleit az adta Ferguson aki a Kolmogorov-konzisztencia-tételt használta, megadta a Dirichlet-folyamat definícióját és leírta a Posterior Dirichlet-folyamatot. Kutatásait folytatva, Blackwell és MacQueen a de Finetti-tételt használta egy ilyen véletlenszerű valószínűségi mérték létezésének bizonyítására, és bevezette a Blackwell-MacQueen urna sémát, amely kielégíti a Dirichlet-folyamat tulajdonságait. 1994-ben Sethuraman egy további egyszerű és közvetlen módot nyújtott a DP felépítésére a Stick-breaking konstrukció bevezetésével. Végül egy másik képviseletet biztosított Aldous aki bemutatta a kínai éttermi folyamatot, mint a Dirichlet-folyamat megalkotásának hatékony módját.

A Dirichlet-folyamat különféle reprezentációi matematikailag ekvivalensek, de megfogalmazásuk eltér, mert különböző nézőpontokból vizsgálják a problémát. Az alábbiakban bemutatjuk a szakirodalomban fellelhető leggyakoribb reprezentációkat, és a kínai éttermi folyamatra összpontosítunk, amely egyszerű és számítási szempontból hatékony módszert kínál a Dirichlet-folyamat következtetési algoritmusainak felépítésére.

3.1 A Blackwell-MacQueen urnaséma

A Blackwell-MacQueen urnaséma használható egy Dirichlet-folyamat ábrázolására, és bevezette Blackwell és MacQueen. A pólyai urnaséma alapján készült, amely a csere nélküli mintavétel ellentétes modelljének tekinthető. A Pólya urna sémában feltételezzük, hogy van egy nem átlátszó urnánk, amely színes golyókat tartalmaz, és véletlenszerűen húzunk golyókat. Amikor rajzolunk egy labdát, figyeljük meg a színét, visszatesszük az urnába, és adunk hozzá még egy ugyanolyan színű labdát. Hasonló sémát használ Blackwell és MacQueen a Dirichlet folyamat megalkotásához.

Ez a séma θ sorozatát állítja elő₁,θ₂,… val vel feltételes valószínűségek . Ebben a sémában feltételezzük, hogy G₀ a színek és minden θ eloszlása_n az urnába helyezett labda színét jelöli. Az algoritmus a következő:

· Egy üres urnával kezdjük.

· -vel arányos valószínűséggel α rajzolunk és egy ilyen színű labdát adunk az urnába.

· Az urnából n-1-gyel arányos valószínűséggel húzunk egy véletlenszerű golyót, megfigyeljük a színét, visszahelyezzük az urnára, és az urnába helyezünk még egy azonos színű labdát.

Korábban egy Dirichlet folyamattal kezdtük, és levezettük a Blackwell-MacQueen sémát. Most kezdjük fordítva a Blackwell-MacQueen sémával, és származtatjuk a DP-t. Mivel θ_i idd módon húztuk G-ből, közös eloszlásuk invariáns lesz minden véges permutációra, így kicserélhetők. Következésképpen a de Finetti-tételt használva azt kapjuk, hogy léteznie kell egy eloszlásnak a mértékek között, hogy id-ek legyenek, és ez az eloszlás a Dirichlet-folyamat. Ennek eredményeként bebizonyítjuk, hogy a Blackwell-MacQueen urnaséma a DP reprezentációja, és konkrét módot ad ennek megalkotására. Amint később látni fogjuk, ez a séma matematikailag egyenértékű a kínai éttermi eljárással.

3.2 A bottörő szerkezet

A pálcikatörő konstrukció egy alternatív módja a Dirichlet-eljárás ábrázolásának, amelyet a Sethuraman. Ez egy konstruktív módja annak kialakításának terjesztését és használja a analógiát követve: Feltételezzük, hogy van egy 1 hosszúságú pálcánk, β pozícióban törjük el₁ és hozzárendeljük a π-t₁ egyenlő a bot azon részének hosszával, amelyet eltörtünk. Ugyanezt a folyamatot megismételjük, hogy megkapjuk a π-t₂, Pi₃,… stb; ennek a sémának a definíciója miatt végtelen ideig folytathatjuk.

A fentiek alapján a π_k mintázható , Ahol a míg az előző sémákhoz hasonlóan a θ-t közvetlenül az alapeloszlás veszi minta . Következésképpen a G eloszlás felírható π-vel súlyozott delta függvények összegeként_k valószínűséggel egyenlő . Így a pálcikatörő konstrukció egyszerű és intuitív módot ad a Dirichlet-folyamat megalkotására.

3.3 A kínai étterem folyamata

A kínai éttermi folyamat, amelyet a Aldous, egy másik hatékony módja a Dirichlet-folyamat ábrázolásának, és közvetlenül összekapcsolható a Blackwell-MacQueen urna sémával. Ez a séma a analógiát követve: Feltételezzük, hogy van egy kínai étterem végtelenül sok asztallal. Ahogy a vásárlók belépnek az étterembe, véletlenszerűen leülnek valamelyik elfoglalt asztalhoz, vagy úgy döntenek, hogy az első szabad asztalhoz ülnek.

A CRP meghatározza a pozitív egész számok partícióinak eloszlását. θ rajzolásával kezdjük₁,…θ_n Blackwell-MacQueen urna sémájából. Amint azt az előző szegmensekben tárgyaltuk, klaszterezési hatást várunk, és így a k egyedi θ értékek összessége jelentősen kevesebb lesz, mint n. Így ez meghatározza az {1,2,…,n} halmaz egy partícióját k klaszterben. Következésképpen a Blackwell-MacQueen urnaséma alapján való rajz az {1,2,…,n} halmaz véletlenszerű partícióját indukálja. A kínai éttermi folyamat ez indukálta partíciók közötti elosztás. Az algoritmus a következő:

· Egy üres étteremmel kezdünk.

· A 1^st az ügyfél mindig az 1-en ül^st táblázat

· Az n+1^th az ügyfélnek 2 lehetősége van:

o Ülj le az 1. üres asztalra valószínûséggel

o Valószínűséggel üljön le a k. foglalt asztalok bármelyikére
ahol az asztalon ülők száma

Ahol α a DP diszperziós értéke, n pedig az étteremben egy adott időpontban tartózkodó vendégek teljes száma. A z látens változó_i tárolja az i táblaszámát^th ügyfél, és 1-től k-ig veszi az értékeket_n ahol k_n az elfoglalt asztalok teljes száma, amikor n ügyfél tartózkodik az étteremben. Meg kell jegyeznünk, hogy a k_n mindig kisebb vagy egyenlő lesz n-nel, és átlagosan kb . Végül meg kell jegyeznünk, hogy a táblázat elrendezésének valószínűsége invariáns a permutációkra. Így a z_i cserélhető, ami azt jelenti, hogy az azonos méretű ügyfelekkel rendelkező asztalok azonos valószínűséggel rendelkeznek.

A kínai éttermi folyamat szorosan kapcsolódik a pólyai urnarendszerhez és a Dirichlet folyamathoz. A CRP egy módja annak, hogy meghatározzuk a partíciók közötti elosztás (tábla-hozzárendelések) n pontból, és priorként használható a z látens változó terében_i ami meghatározza a klaszter hozzárendeléseket. A CRP ekvivalens Pólya urnasémájával, azzal a különbséggel, hogy nem rendel paramétereket minden táblához/klaszterhez. Menni a CRP-től Pólya urnasémájáig rajzolunk minden táblára k=1,2…, majd minden x-re_i amely a z táblázatba van csoportosítva_i hozzárendelni a . Más szóval hozzárendelni az új x-hez_i a táblázat θ paramétere. Végre azóta nem tudunk hozzárendelni a θ-t a végtelen asztalokhoz a kezdetektől fogva, minden alkalommal hozzárendelhetünk egy új θ-t, amikor valaki új asztalra ül. A fentiek miatt a CRP segíthet számításilag hatékony algoritmusok felépítésében, amelyek segítségével fürtelemzést végezhetünk az adatkészleteken.

Ebben a bejegyzésben a Dirichlet-folyamatot és annak felépítésének számos módját tárgyaltuk. A fenti ötleteket a következő cikkben fogjuk használni. Bemutatjuk a Dirichlet-folyamat-keverékmodellt, és a kínai étterem-reprezentációt fogjuk használni a Dirichlet-folyamat és az előforma-klaszter elemzés elkészítéséhez. Ha néhány pontot kihagyott, ne aggódjon, mert a következő két cikkben a dolgok világosabbá válnak.

Remélem érdekesnek találtad ezt a bejegyzést. Ha igen, szánjon egy percet és ossza meg a Facebookon és a Twitteren. 🙂