A kvantumdinamika mérőképe

A kvantumdinamika mérőképe

Időbélyeg: 21. március 2024. 6:43

Kevin Slagle

Electrical and Computer Engineering Department, Rice University, Houston, Texas, 77005 USA
Fizikai Tanszék, California Institute of Technology, Pasadena, California 91125, USA
Institute for Quantum Information and Matter és Walter Burke Institute for Theoretical Physics, California Institute of Technology, Pasadena, California 91125, USA

Érdekesnek találja ezt a cikket, vagy szeretne megvitatni? Scite vagy hagyjon megjegyzést a SciRate-en.

Absztrakt

Bár a helyi hamiltoniak helyi idődinamikát mutatnak, ez a lokalitás nem egyértelmű a Schrödinger-képben abban az értelemben, hogy a hullámfüggvény amplitúdói nem engedelmeskednek a lokális mozgásegyenletnek. Megmutatjuk, hogy a geometriai lokalitás explicit módon elérhető a mozgásegyenletekben, ha a kvantummechanika globális unitárius invarianciáját lokális nyomtávú invarianciává „mérjük”. Ez azt jelenti, hogy a $langle psi|A|psi rangle$ várható értékek invariánsak a $|psirangle az U |psirangle$ hullámfüggvényre és a $A operátorok az UAU^dagger$ hullámfüggvényre ható globális egységtranszformáció alatt, és megmutatjuk, hogy ez lehetséges. hogy ezt a globális invarianciát lokális szelvényváltozatlansággá mérjük. Ehhez lecseréljük a hullámfüggvényt a $|psi_Jrangle$ lokális hullámfüggvények gyűjteményére, egyet a $J$ tér minden egyes foltjára. A térfoltok gyűjteményét úgy választjuk, hogy a teret lefedje; pl. kiválaszthatjuk a foltokat, hogy egyedi qubitek vagy legközelebbi szomszédos helyek legyenek egy rácson. A szomszédos $I$ és $J$ térfoltpárokhoz társított lokális hullámfüggvények a $U_{IJ}$ dinamikus unitárius transzformációkkal kapcsolódnak egymáshoz. A lokális hullámfüggvények lokálisak abban az értelemben, hogy dinamikájuk lokális. Ez azt jelenti, hogy a $|psi_Jrangle$ lokális hullámfüggvények és a $U_{IJ}$ kapcsolatok mozgásegyenletei kifejezetten lokálisak a térben, és csak a közeli Hamilton-feltételektől függenek. (A lokális hullámfüggvények soktestes hullámfüggvények, és ugyanazzal a Hilbert-térdimenzióval rendelkeznek, mint a szokásos hullámfüggvénynek.) A kvantumdinamika ezt a képét mérőképnek nevezzük, mivel lokális szelvény-invarianciát mutat. Egyetlen térbeli folt lokális dinamikája az interakciós képhez kapcsolódik, ahol a Hamilton-féle interakció csak a közeli Hamilton-termékekből áll. Az explicit lokalitást általánosíthatjuk úgy is, hogy a lokalitást belefoglaljuk a lokális töltés- és energiasűrűségbe.

The Gauge Picture of Quantum Dynamics PlatoBlockchain Data Intelligence. Vertical Search. Ai.

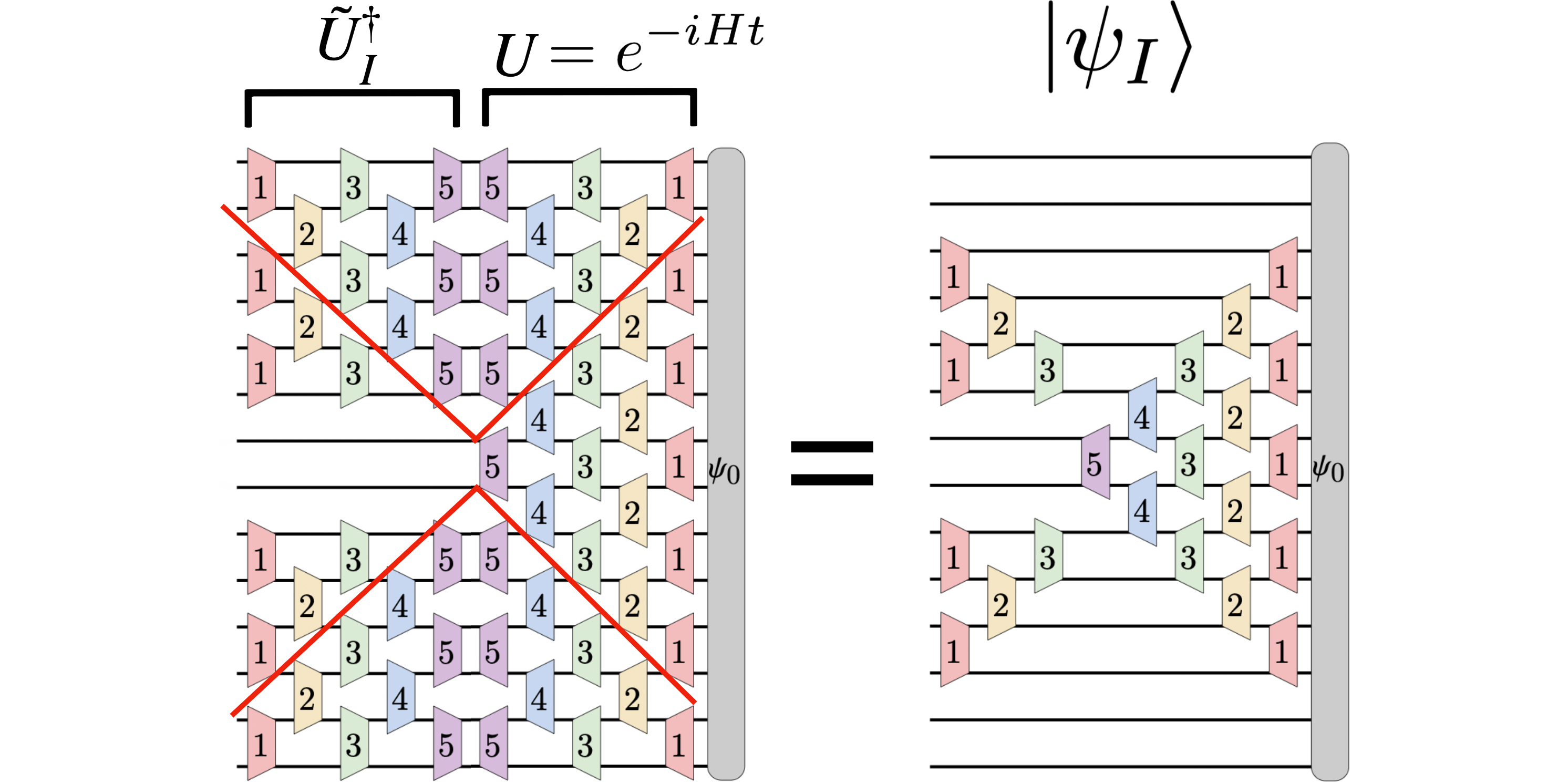
Kiemelt kép: Schrodinger képén a $|psi_0rangle$ kezdeti hullámfüggvény $U(t) |psi_0rangle$-ra fejlődik egy $t$ idő után, ahol $U(t) = e^{-iHt}$ az egységnyi időbeli evolúció. operátor. A mérőkép ehelyett a $|psi_I(t)rangle$ lokális hullámfüggvényeket veszi figyelembe, amelyek egy $I$ részhalmazhoz (vagy folthoz) vannak társítva a térben. A $|psi_I(t)rangle = tilde{U}_I^dagger(t) |psi(t)rangle$ időbeli lokális hullámfüggvényt a $|psi(t)rangle = U(t) |psi_0rangle Schrodinger-féle hullámfüggvényből kapjuk. $ a $tilde{U}_I^dagger(t)$ egységes operátoron keresztül, amely megfordítja az idő alakulását a $I$ régión kívül. Ennek eredményeként a $partial_I |psi_I(t)rangle$ lokális hullámfüggvény dinamikája csak a közeli Hamilton-tagoktól függ, amelyek átfedik az $I$ régiót. Az ábra ezeket az egységes operátorokat kvantumáramkörökként ábrázolja, és bemutatja, hogy a $U(t)$-ból származó időfejlődés nagy része kiesik $tilde{U}_I^dagger(t)$-val, így csak egy homokóra alakú időfejlődési operátor marad. a kezdeti hullámfüggvényre ható (az ábra jobb oldalán). Ez a homokóra alakú kezelő a Heisenberg képén látható fénykúp alakú operátor növekedéssel analóg.

Népszerű összefoglaló

A kvantumdinamika két leghíresebb képe a Schrodinger és a Heisenberg kép. Schrodinger képén a hullámfüggvény időben fejlődik, míg Heisenberg képén a hullámfüggvény állandó, de az operátorok időben fejlődnek. Ebben a munkában bemutatjuk a kvantumdinamikának egy új képét, a mérőképet, amely mély összefüggéseket teremt az információ lokalitásával és a mérőszám elmélettel.

A lokalitás kapcsán: Heisenberg képének szép előnye, hogy a lokalitás kifejezett a mozgásegyenletekben. Vagyis egy helyi szolgáltató időbeli alakulása csak a közeli helyi szolgáltatók állapotától függ. Ezzel szemben a lokalitás nem ily módon kifejezett Schrodinger képében, amelyre egyetlen hullámfüggvény létezik, amelynek idődinamikája a térben mindenhol operátoroktól függ. Az új mérőképünk úgy módosítja Schrodinger képét, hogy ki tudjuk számítani a „lokális hullámfüggvényt”, amely ugyanazt az információt hordozza, mint a Schrodinger-féle hullámfüggvény, és arra számíthatunk, hogy a lokális hullámfüggvények idődinamikája a mérőképen csak a közeli Hamilton-termékektől függ, ami a lokalitást explicitté teszi a mozgásegyenletek. Ennek az explicit lokalitásnak az elérése érdekében a szelvénykép mérőmezőket ad a mozgásegyenletekhez.

A szelvényelmélet mély kapcsolatot létesít egy globális szimmetriával rendelkező Hamilton-féle (vagy Lagrange-féle) és egy másik Hamilton-féle között, ahol a globális szimmetriát egy lokális szelvényszimmetria váltja fel a hozzáadott dinamikus mérőmezők révén. Érdekes módon a $ihbar parciális_t |psirangle = H |psirangle$ Schrodinger egyenlete a $|psirangle U |psirangle$ és $H UHU^dagger$ transzformációja által adott globális unitárius invarianciát ismeri el. Munkánk azt mutatja, hogy a Schrodinger-egyenletben erre a globális invarianciára is lehet szelvényelméletet alkalmazni, hogy egy új mozgásegyenletet, azaz a szelvényképet kapjunk dinamikus szelvénymezőkkel és lokális szelvényinvarianciával.

► BibTeX adatok

► Referenciák

[1] David Deutsch és Patrick Hayden. „Információáramlás összefonódott kvantumrendszerekben”. Proceedings of the Royal Society of London Series A 456, 1759 (2000). arXiv:quant-ph/9906007.
https://​/​doi.org/​10.1098/​rspa.2000.0585
arXiv:quant-ph/9906007

[2] Michael A. Levin és Xiao-Gang Wen. „String-net kondenzáció: A topológiai fázisok fizikai mechanizmusa”. Phys. Rev. B 71, 045110 (2005). arXiv:cond-mat/​0404617.
https://​/​doi.org/​10.1103/​PhysRevB.71.045110
arXiv:cond-mat/0404617

[3] T. Senthil, Ashvin Vishwanath, Leon Balents, Subir Sachdev és Matthew PA Fisher. „Meghatározott kvantumkritikus pontok”. Science 303, 1490–1494 (2004). arXiv:cond-mat/​0311326.
https://​/​doi.org/​10.1126/​science.1091806
arXiv:cond-mat/0311326

[4] Beni Yoshida. „Egzotikus topológiai rend fraktál spin folyadékokban”. Phys. Rev. B 88, 125122 (2013). arXiv:1302.6248.
https://​/​doi.org/​10.1103/​PhysRevB.88.125122
arXiv: 1302.6248

[5] Kevin Hartnett. „A mátrixszorzás hüvelykekkel közelebb van a mitikus célhoz”. Quanta Magazin (2021). url: https://​/​www.quantamagazine.org/​mathematicians-inch-closer-to-matrix-multiplication-goal-20210323/​.
https://​/​www.quantamagazine.org/​mathematicians-inch-closer-to-matrix-multiplication-goal-20210323/​

[6] Volker Strassen. „A Gauss-elimináció nem optimális”. Numerische Mathematik 13, 354–356 (1969).
https://​/​doi.org/​10.1007/​BF02165411

[7] Kevin Slagle. „Kvantummérő hálózatok: újfajta tenzorhálózat”. Quantum 7, 1113 (2023). arXiv:2210.12151.
https:/​/​doi.org/​10.22331/​q-2023-09-14-1113
arXiv: 2210.12151

[8] Román Orús. „Gyakorlati bevezetés a tenzorhálózatokba: Mátrix szorzatállapotok és vetített összefonódott pár állapotok”. Annals of Physics 349, 117–158 (2014). arXiv:1306.2164.
https://​/​doi.org/​10.1016/​j.aop.2014.06.013
arXiv: 1306.2164

[9] Michael P. Zaletel és Frank Pollmann. „Izometrikus tenzorhálózat állapotai két dimenzióban”. Phys. Rev. Lett. 124, 037201 (2020). arXiv:1902.05100.
https://​/​doi.org/​10.1103/​PhysRevLett.124.037201
arXiv: 1902.05100

[10] Steven Weinberg. „A kvantummechanika tesztelése”. Annals of Physics 194, 336–386 (1989).
https:/​/​doi.org/​10.1016/​0003-4916(89)90276-5

[11] N. Gisin. „Weinberg nemlineáris kvantummechanikája és szupraluminális kommunikációja”. Physics Letters A 143, 1–2 (1990).
https:/​/​doi.org/​10.1016/​0375-9601(90)90786-N

[12] József Polchinski. „Weinberg nemlineáris kvantummechanikája és az Einstein-Podolsky-Rosen paradoxon”. Phys. Rev. Lett. 66, 397-400 (1991).
https://​/​doi.org/​10.1103/​PhysRevLett.66.397

[13] Kevin Slagle. „Kvantummechanika tesztelése zajos kvantumszámítógépekkel” (2021). arXiv:2108.02201.
arXiv: 2108.02201

[14] Brian Swingle. „Az időn kívüli korrelátorok fizikájának megfejtése”. Nature Physics 14, 988–990 (2018).
https:/​/​doi.org/​10.1038/​s41567-018-0295-5

[15] Ignacio García-Mata, Rodolfo A. Jalabert és Diego A. Wisniacki. „Időn kívüli korrelátorok és kvantumkáosz” (2022). arXiv:2209.07965.
arXiv: 2209.07965

[16] Rahul Nandkishore és David A. Huse. „Sok test lokalizációja és termizálása a kvantumstatisztikai mechanikában”. Annual Review of Condensed Matter Physics 6, 15–38 (2015). arXiv:1404.0686.
https://​/​doi.org/​10.1146/​annurev-conmatphys-031214-014726
arXiv: 1404.0686

[17] Dmitry A. Abanin, Ehud Altman, Immanuel Bloch és Maksym Serbyn. „Kollokvium: Sok test lokalizációja, termizálása és összefonódása”. Reviews of Modern Physics 91, 021001 (2019). arXiv:1804.11065.
https://​/​doi.org/​10.1103/​RevModPhys.91.021001
arXiv: 1804.11065

[18] Bruno Nachtergaele és Robert Sims. „Much Ado About Something: Miért hasznosak a Lieb-Robinson korlátok” (2011). arXiv:1102.0835.
arXiv: 1102.0835

[19] Daniel A. Roberts és Brian Swingle. „Lieb-robinson kötés és a pillangóeffektus a kvantumtérelméletekben”. Phys. Rev. Lett. 117, 091602 (2016). arXiv:1603.09298.
https://​/​doi.org/​10.1103/​PhysRevLett.117.091602
arXiv: 1603.09298

[20] Zhiyuan Wang és Kaden RA Hazzard. „A lieb-robinson kötés szigorítása a lokálisan kölcsönható rendszerekben”. PRX Quantum 1, 010303 (2020). arXiv:1908.03997.
https://​/​doi.org/​10.1103/​PRXQuantum.1.010303
arXiv: 1908.03997

Idézi

[1] Sayak Guha Roy és Kevin Slagle, „Interpoláció a kvantumdinamika mérőműszer és Schrödinger képei között”, SciPost Physics Core 6 4, 081 (2023).

[2] Kevin Slagle, „Quantum Gauge Networks: A New Kind of Tensor Network”, Quantum 7, 1113 (2023).

A fenti idézetek innen származnak SAO/NASA HIRDETÉSEK (utolsó sikeres frissítés: 2024-03-22 22:55:39). Előfordulhat, hogy a lista hiányos, mivel nem minden kiadó ad megfelelő és teljes hivatkozási adatokat.

On Crossref által idézett szolgáltatás művekre hivatkozó adat nem található (utolsó próbálkozás 2024-03-22 22:55:38).

Ez a tanulmány a Quantumban jelent meg Creative Commons Nevezd meg 4.0 International (CC BY 4.0) engedély. A szerzői jog az eredeti szerzői jog tulajdonosainál marad, például a szerzőknél vagy intézményeiknél.

Időbélyeg:

Még több Quantum Journal