A kvantumállapotok koncentrációs határai és a polinomiális közelítésekből származó QAOA korlátai

Újra kiadta Platón

Követő: 0

Concentration bounds for quantum states and limitations on the QAOA from polynomial approximations PlatoBlockchain Data Intelligence. Vertical Search. Ai.

Anurag Anshu¹ és Tony Metger²

¹Műszaki és Alkalmazott Tudományok Iskola, Harvard Egyetem
²Institute for Theoretical Physics, ETH Zürich

Érdekesnek találja ezt a cikket, vagy szeretne megvitatni? Scite vagy hagyjon megjegyzést a SciRate-en.

Absztrakt

Koncentrációs korlátokat bizonyítunk a következő kvantumállapot-osztályokra: (i) sekély kvantumáramkörök kimeneti állapotai, válaszolva egy nyitott kérdésre [16]; (ii) az injektív mátrix szorzatállapotai; (iii) a sűrű Hamilton-evolúció kimeneti állapotai, azaz $e^{iota H^{(p)}} cdots e^{iota H^{(1)}} |psi_0rangle$ alakú állapotok bármely $n$- esetén qubit szorzatállapot $|psi_0rangle$, ahol minden $H^{(i)}$ lehet bármely lokális ingázási Hamilton-féle, amely eleget tesz egy normakényszernek, beleértve a sűrű Hamiltonokat is, ahol bármilyen qubit kölcsönhatásba lép. Bizonyításaink polinomiális közelítéseket használnak annak kimutatására, hogy ezek az állapotok közel állnak a helyi operátorokhoz. Ez azt jelenti, hogy a számítási alapmérés Hamming-súlyának eloszlása (és más kapcsolódó megfigyelhető adatok) koncentrálódik.
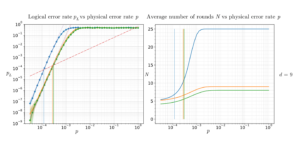
A (iii) példa a kvantumközelítő optimalizálási algoritmus (QAOA) által előállított állapotok. Az ezekre az állapotokra vonatkozó koncentrációs eredményeinket felhasználva megmutatjuk, hogy véletlen spin modell esetén a QAOA még szuperkonstans $p = o(log log n)$ szinten is csak elhanyagolható valószínűséggel sikerülhet, feltételezve az ún. átfedési rés tulajdonságnak nevezzük. Ez adja a QAOA első korlátait a sűrű példányokon szuperkonstans szinten, javítva a legutóbbi eredményt [BGMZ22].

[Beágyazott tartalmat]

► BibTeX adatok

@ cikk a kvantumállapotok és a polinomiális közelítésekből származó {QAOA} korlátai} szerző = {Anshu, Anurag és Metger, Tony}, folyóirat = {{Quantum}}, issn = {2023-10.22331X}, kiadó = {{Verein zur F {“{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}, kötet = {2023}, oldal = {05}, hónap = május, év = {11} }

► Referenciák

[1] Anurag Anshu, Itai Arad és David Gosset. Területi törvény a 2D frusztrációmentes pörgetési rendszerekhez. In Proceedings of the 54th Annual ACM SIGACT Symposium on Theory of Computing, STOC 2022, 12–18. oldal, New York, NY, USA, 2022. Association for Computing Machinery. doi:10.1145/3519935.3519962.
https:///doi.org/10.1145/3519935.3519962

[2] Anurag Anshu és Nikolas P. Breuckmann. A kombinatorikus NLTS konstrukciója. Journal of Mathematical Physics, 63(12), 12, 2022. doi:10.1063/5.0113731.
https:///doi.org/10.1063/5.0113731

[3] Anurag Anshu, Nikolas Breuckmann és Chinmay Nirkhe. NLTS hamiltoniak jó kvantumkódokból. arXiv preprint arXiv:2206.13228, 2022. URL: https:///arxiv.org/abs/2206.13228.
arXiv: 2206.13228

[4] Nilin Abrahamsen. A helyi hamiltoniak számára kötött spektrális csernoff rövid bizonyítéka. arXiv preprint arXiv:2009.04993, 2020. URL: https:///arxiv.org/abs/2009.04993.
arXiv: 2009.04993

[5] Álvaro M Alhambra. Kvantum soktestes rendszerek termikus egyensúlyban. arXiv preprint arXiv:2204.08349, 2022. URL: https:///arxiv.org/abs/2204.08349.
arXiv: 2204.08349

[6] Anurag Anshu és Chinmay Nirkhe. Áramkör alsó határai a kvantumkód hamiltoniak alacsony energiájú állapotaihoz. In Mark Braverman, szerkesztő, 13. Innovations in Theoretical Computer Science Conference (ITCS 2022), Leibniz International Proceedings in Informatics (LIPIcs) 215. kötete, 6:1–6:22 oldal, Dagstuhl, Németország, 2022. Schloss Dagstuhl – Leibniz- Zentrum für Informatik. doi:10.4230/LIPIcs.ITCS.2022.6.
https:///doi.org/10.4230/LIPIcs.ITCS.2022.6

[7] Anurag Anshu. Véges korrelációs hosszúságú kvantumállapotok koncentrációhatárai kvantum spinrácsrendszereken. New Journal of Physics, 18(8):083011, 2016. aug. doi:10.1088/1367-2630/18/8/083011.
https://doi.org/10.1088/1367-2630/18/8/083011

[8] Fernando GSL Brandao és Marcus Cramer. Statisztikai mechanikai együttesek ekvivalenciája nem kritikus kvantumrendszerekhez. arXiv preprint arXiv:1502.03263, 2015. URL: https:///arxiv.org/abs/1502.03263.
arXiv: 1502.03263

[9] H. Buhrman, R. Cleve, R. De Wolf és C. Zalka. Határok kis hibás és nulla hibás kvantumalgoritmusokhoz. In Proceedings of the 40th Annual Symposium on Foundations of Computer Science, 358–368. oldal, 1999. doi:10.1109/SFFCS.1999.814607.
https:///doi.org/10.1109/SFFCS.1999.814607

[10] FGSL Brandao, Marcus Cramer és Madalin Guta. Egy berry–esseen tétel kvantumrácsrendszerekre és a statisztikai mechanikai együttesek ekvivalenciájára. QIP2015 Talk, 2015. URL: http:///www.quantum-lab.org/qip2015/talks/125-Brandao.pdf.
http:///www.quantum-lab.org/qip2015/talks/125-Brandao.pdf

[11] Joao Basso, David Gamarnik, Song Mei és Leo Zhou. A qaoa teljesítménye és korlátai állandó szinten nagy ritka hipergráfokon és forgóüveg modelleken. 2022-ben az IEEE 63. éves szimpóziuma a számítástechnika alapjairól (FOCS), 2022. doi:10.1109/FOCS54457.2022.00039.
https:///doi.org/10.1109/FOCS54457.2022.00039

[12] Sergey Bravyi, Alexander Kliesch, Robert Koenig és Eugene Tang. A variációs kvantumoptimalizálás akadályai a szimmetriavédelemből. Phys. Rev. Lett., 125:260505, Dec. doi:10.1103/PhysRevLett.125.260505.
https:///doi.org/10.1103/PhysRevLett.125.260505

[13] Wei-Kuo Chen, David Gamarnik, Dmitry Panchenko és Mustazee Rahman. A lokális algoritmusok szuboptimalitása a max-cut problémák egy osztályához. The Annals of Probability, 47(3):1587 – 1618, 2019. doi:10.1214/18-AOP1291.
https:///doi.org/10.1214/18-AOP1291

[14] Chi-Ning Chou, Peter J. Love, Juspreet Singh Sandhu és Jonathan Shi. A lokális kvantum algoritmusok korlátai véletlenszerű MAX-k-XOR és azon túl. 49. Nemzetközi Kollokvium automatákról, nyelvekről és programozásról (ICALP 2022), Leibniz International Proceedings in Informatics (LIPIcs) 229. kötete, 41:1–41:20, Dagstuhl, Németország, 2022. Schloss Dagstuhl – Leibniz-Zen Informatik. doi:10.4230/LIPIcs.ICALP.2022.41.
https:///doi.org/10.4230/LIPIcs.ICALP.2022.41

[15] J Ignacio Cirac, David Perez-Garcia, Norbert Schuch és Frank Verstraete. Mátrixszorzatállapotok és vetített összefonódott pár állapotok: Fogalmak, szimmetriák, tételek. Reviews of Modern Physics, 93(4):045003, 2021. doi:10.1103/RevModPhys.93.045003.
https:///doi.org/10.1103/RevModPhys.93.045003

[16] Giacomo De Palma, Milad Marvian, Cambyse Rouzé és Daniel Stilck Franca. A variációs kvantum algoritmusok korlátai: Kvantumoptimális transzport megközelítés. PRX Quantum, 4:010309, 2023. január. doi:10.1103/PRXQuantum.4.010309.
https:///doi.org/10.1103/PRXQuantum.4.010309

[17] Giacomo De Palma és Cambyse Rouzé. Kvantumkoncentrációs egyenlőtlenségek. Annales Henri Poincaré, 2022. április, doi: 10.1007/s00023-022-01181-1.
https://doi.org/10.1007/s00023-022-01181-1

[18] L. Eldar és AW Harrow. Helyi hamiltoniak, amelyek alapállapotát nehéz közelíteni. 2017-ben az IEEE 58. éves szimpóziuma a számítástechnika alapjairól (FOCS), 427–438. oldal, 2017. doi:10.1109/FOCS.2017.46.
https:///doi.org/10.1109/FOCS.2017.46

[19] Edward Farhi, Jeffrey Goldstone és Sam Gutmann. Egy kvantumközelítő optimalizálási algoritmus. arXiv preprint arXiv:1411.4028, 2014. URL: https:///arxiv.org/abs/1411.4028.
arXiv: 1411.4028

[20] Edward Farhi, David Gamarnik és Sam Gutmann. A kvantumközelítő optimalizáló algoritmusnak látnia kell a teljes gráfot: Tipikus eset. arXiv preprint arXiv:2004.09002, 2020. URL: https:///arxiv.org/abs/2004.09002.
arXiv: 2004.09002

[21] David Gamarnik. Az átfedési hézag tulajdonsága: Topológiai akadály a véletlenszerű struktúrák feletti optimalizáláshoz. Proceedings of the National Academy of Sciences, 118(41):e2108492118, 2021. doi:10.1073/pnas.2108492118.
https:///doi.org/10.1073/pnas.2108492118

[22] Ronald L Graham, Martin Grötschel és Lovász László. Handbook of Combinatorics, 1. kötet, Elsevier, 1995.

[23] David Gamarnik és Aukosh Jagannath. Az átfedési hézag tulajdonsága és a hozzávetőleges üzenetátadási algoritmusok $p$-spin modellekhez. The Annals of Probability, 49(1):180–205, 2021. URL: https://hdl.handle.net/1721.1/145311.
https:///hdl.handle.net/1721.1/145311

[24] David Gamarnik, Aukosh Jagannath és Alexander S Wein. Véletlenszerű optimalizálási problémák alacsony fokú keménysége. 2020-ban az IEEE 61. éves szimpóziuma a számítástechnika alapjairól (FOCS), 131–140. oldal. IEEE, 2020. doi:10.1109/FOCS46700.2020.00021.
https:///doi.org/10.1109/FOCS46700.2020.00021

[25] David Gamarnik és Quan Li. Egy gauss véletlen mátrix nagy almátrixának megtalálása. The Annals of Statistics, 46(6A):2511–2561, 2018. URL: http:///hdl.handle.net/1721.1/120593.
http:///hdl.handle.net/1721.1/120593

[26] Francesco Guerra és Fabio Lucio Toninelli. A termodinamikai határ átlagos terepi forgású üvegmodellekben. Communications in Mathematical Physics, 230(1):71–79, 2002. doi:10.1007/s00220-002-0699-y.
https:///doi.org/10.1007/s00220-002-0699-y

[27] D. Goderis és P. Vets. Központi határelv tétel kvantumrendszerek keverésére és a fluktuációk CCR-algebraira. Communications in Mathematical Physics, 122:249–265, 1989. doi: 10.1007/BF01257415.
https:///doi.org/10.1007/BF01257415

[28] MB Hastings. Lieb-schultz-mattis magasabb dimenziókban. Phys. Rev. B, 69:104431, 2004. márc. doi:10.1103/PhysRevB.69.104431.
https:///doi.org/10.1103/PhysRevB.69.104431

[29] Michael Hartmann, Günter Mahler és Ortwin Hess. A hőmérséklet megléte a nanoskálán. Phys. Rev. Lett., 93:080402, 2004. augusztus. doi:10.1103/PhysRevLett.93.080402.
https:///doi.org/10.1103/PhysRevLett.93.080402

[30] Tomotaka Kuwahara, Itai Arad, Luigi Amico és Vlatko Vedral. Több test alapállapotainak lokális reverzibilitása és összefonódási szerkezete. Quantum Science and Technology, 2(1):015005, 2017. doi:10.1088/2058-9565/aa523d.
https:///doi.org/10.1088/2058-9565/aa523d

[31] Jeff Kahn, Nathan Linial és Alex Samorodnitsky. Belefoglalás-kizárás: Pontos és hozzávetőleges. Combinatorica, 16(4):465–477, 1996. december doi:10.1007/BF01271266.
https:///doi.org/10.1007/BF01271266

[32] Tomotaka Kuwahara és Keiji Saito. Saját állapotú termizáció a korreláció klaszterezési tulajdonságából. Phys. Rev. Lett., 124:200604, 2020. május. doi:10.1103/PhysRevLett.124.200604.
https:///doi.org/10.1103/PhysRevLett.124.200604

[33] Tomotaka Kuwahara és Keiji Saito. Gauss-koncentrációhoz kötött és együttes ekvivalencia általános kvantum-többtest-rendszerekben, beleértve a hosszú távú kölcsönhatásokat. Annals of Physics, 421:168278, 2020. doi:10.1016/j.aop.2020.168278.
https:///doi.org/10.1016/j.aop.2020.168278

[34] Tomotaka Kuvahara. Különböző operátorok valószínűségi eloszlásának összekapcsolása és a chernoff-hoeffding egyenlőtlenség általánosítása. Journal of Statistical Mechanics: Theory and Experiment, 2016(11):113103, nov 2016. doi:10.1088/1742-5468/2016/11/113103.
https://doi.org/10.1088/1742-5468/2016/11/113103

[35] Elliott Lieb, Theodore Schultz és Daniel Mattis. Egy antiferromágneses lánc két oldható modellje. Annals of Physics, 16(3):407–466, 1961. doi:10.1016/0003-4916(61)90115-4.
https://doi.org/10.1016/0003-4916(61)90115-4

[36] Anthony Leverrier és Gilles Zémor. Kvantumbarnító kódok. 2022-ben az IEEE 63. éves szimpóziuma a számítástechnika alapjairól (FOCS), 2022. doi:10.1109/FOCS54457.2022.00117.
https:///doi.org/10.1109/FOCS54457.2022.00117

[37] D. Perez-Garcia, F. Verstraete, MM Wolf és JI Cirac. Mátrix szorzat állapotábrázolások. Quantum Info. Comput., 7(5):401–430, 2007. július. URL: https:///dl.acm.org/doi/10.5555/2011832.2011833.
https:///dl.acm.org/doi/10.5555/2011832.2011833

[38] Pavel Pantelejev és Gleb Kalachov. Aszimptotikusan jó kvantum és lokálisan tesztelhető klasszikus ldpc kódok. In Proceedings of the 54th Annual ACM SIGACT Symposium on Theory of Computing, 375–388. oldal, 2022. doi:10.1145/3519935.3520017.
https:///doi.org/10.1145/3519935.3520017

[39] Sushant Sachdeva és Nisheeth K. Vishnoi. Gyorsabb algoritmusok közelítéselméleten keresztül. Foundations and Trends® in Theoretical Computer Science, 9(2):125–210, 2014. doi:10.1561/0400000065.
https:///doi.org/10.1561/0400000065

[40] Hal Tasaki. A kanonikus és a mikrokanonikus együttesek lokális ekvivalenciájáról kvantum spin rendszerekre. Journal of Statistical Physics, 172(4):905–926, 2018. augusztus. doi:10.1007/s10955-018-2077-y.
https:///doi.org/10.1007/s10955-018-2077-y

Idézi

[1] Giacomo De Palma, Milad Marvian, Cambyse Rouzé és Daniel Stilck França, „Limitations of Variational Quantum Algorithms: A Quantum Optimal Transport Approach” PRX Quantum 4 1, 010309 (2023).

[2] Ojas Parekh, „Synergies Between Operations Research and Quantum Information Science”, arXiv: 2301.05554, (2023).

[3] Dominik S. Wild és Álvaro M. Alhambra, „Classical simulation of short-time quantum dynamics”, arXiv: 2210.11490, (2022).

[4] Lennart Bittel, Sevag Gharibian és Martin Kliesch: „A variációs kvantum algoritmusok mélységének optimalizálása erősen QCMA-val nehezen közelíthető”, arXiv: 2211.12519, (2022).

A fenti idézetek innen származnak SAO/NASA HIRDETÉSEK (utolsó sikeres frissítés: 2023-05-11 10:33:33). Előfordulhat, hogy a lista hiányos, mivel nem minden kiadó ad megfelelő és teljes hivatkozási adatokat.

Nem sikerült lekérni Az adatok által hivatkozott kereszthivatkozás utolsó próbálkozáskor 2023-05-11 10:33:31: Nem sikerült lekérni a 10.22331/q-2023-05-11-999 hivatkozás által hivatkozott adatokat a Crossref-től. Ez normális, ha a DOI-t nemrég regisztrálták.

Ez a tanulmány a Quantumban jelent meg Creative Commons Nevezd meg 4.0 International (CC BY 4.0) engedély. A szerzői jog az eredeti szerzői jog tulajdonosainál marad, például a szerzőknél vagy intézményeiknél.

SEO által támogatott tartalom és PR terjesztés. Erősödjön még ma.
PlatoAiStream. Web3 adatintelligencia. Felerősített tudás. Hozzáférés itt.
A jövő pénzverése – Adryenn Ashley. Hozzáférés itt.
Részvények vásárlása és eladása PRE-IPO társaságokban a PREIPO® segítségével. Hozzáférés itt.
Forrás: https://quantum-journal.org/papers/q-2023-05-11-999/

Időbélyeg: May 11, 2023

Újra kiadta Platón

Absztrakt

► BibTeX adatok

► Referenciák

Idézi

Átalakítások kvantumhálózatokban lokális műveleteken keresztül, amelyeket a klasszikus kommunikáció véges sok köre segít

A többrészes összefonódás topológiai kapcsolati modelljei

Összeállíthatóan biztonságos eszközfüggetlen titkosítás tanúsított törléssel

LIMDD: Döntési diagram a kvantumszámítás szimulációjához, beleértve a stabilizáló állapotokat

Általános kvantum-algoritmusok Hamilton-szimulációhoz nem Abel-féle rácsmérő elmélet alkalmazásaival

A koherenciaelmélet szerepe az attraktor kvantum neurális hálózatokban

Adaptív szindróma mérések Shor-stílusú hibajavításhoz

Egy pár mérési felület kódja ötszögeken

Hatékony algoritmusok a kvantuminformáció szűk keresztmetszetére

Kvantumkapuk véletlenszerű univerzális halmazainak mátrixkoncentrációs egyenlőtlenségei és hatékonysága

Megőrző térképek rendelése kvantumméréseken

Rólunk

Vertical Search & Ai

Emelvény

Maradjon kapcsolatban

Fiók