Megnövelt pontosság az ügetőszimulációkhoz Csebisev-interpoláció segítségével

Újra kiadta Platón

Követő: 0

Gumaro Rendon¹, Jacob Watkins²és Nathan Wiebe^3,4

¹Zapata Computing Inc., Boston, MA 02110, USA
²Ritka izotópnyalábok létesítménye, Michigan State University, East Lansing, MI 48824, USA
³Számítástechnikai Tanszék, Torontói Egyetem, Toronto, ON M5S 2E4, Kanada
⁴Pacific Northwest National Laboratory, Richland, WA 99352, USA

Érdekesnek találja ezt a cikket, vagy szeretne megvitatni? Scite vagy hagyjon megjegyzést a SciRate-en.

Absztrakt

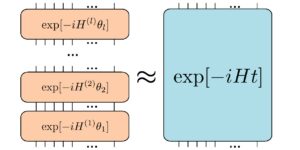
A kvantummetrológia lehetővé teszi a kvantumrendszer tulajdonságainak mérését az optimális Heisenberg-határon. Ha azonban a releváns kvantumállapotokat digitális Hamilton-szimulációval készítjük elő, a felhalmozódott algoritmushibák eltéréseket okoznak ettől az alapvető határtól. Ebben a munkában bemutatjuk, hogy a Trotterizált időfejlődésből adódó algoritmikus hibák hogyan mérsékelhetők standard polinomiális interpolációs technikák használatával. Megközelítésünk az, hogy nulla Trotter lépésméretre extrapolálunk, ami hasonló a nulla zajos extrapolációs technikákhoz a hardverhibák enyhítésére. Szigorú hibaelemzést végzünk az interpolációs megközelítésben a sajátértékek és az időbeli várható várható értékek becslésére, és megmutatjuk, hogy a Heisenberg-határértéket a hiba polilogaritmikus tényezőiig elérjük. Munkánk azt sugallja, hogy a legmodernebb szimulációs algoritmusokéhoz közeli pontosság érhető el a Trotter és a klasszikus erőforrások használatával számos releváns algoritmusos feladathoz.

Improved Accuracy for Trotter Simulations Using Chebyshev Interpolation PlatoBlockchain Data Intelligence. Vertical Search. Ai.

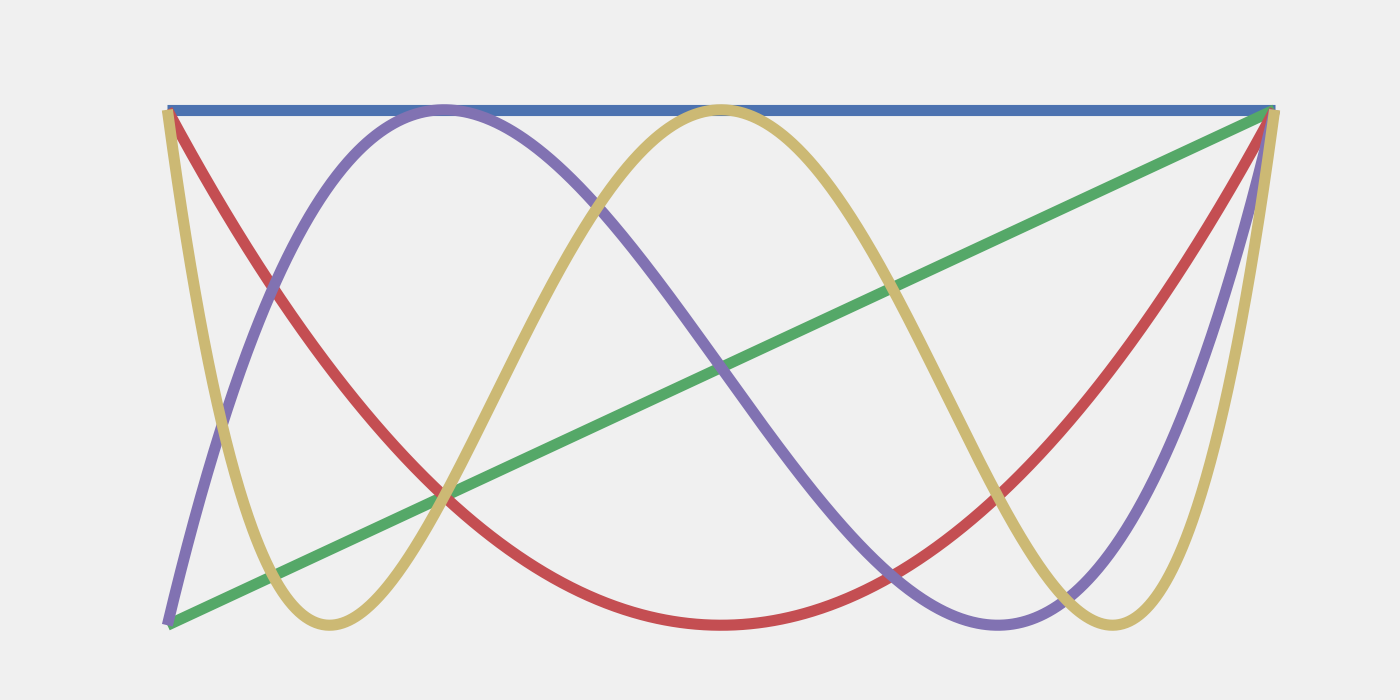
Kiemelt kép: Az első öt Csebisev-polinom. Az interpoláció a Csebisev nulláknál robusztus sémaként szolgál az Trotter-hiba mérséklésére.

[Beágyazott tartalmat]

Népszerű összefoglaló

A kvantumszámítógépek a továbbfejlesztett kvantumszimuláció révén javíthatják a kémia, az anyagok, a magfizika és más tudományos tudományterületek megértését. Számos kvantum-algoritmus létezik erre a feladatra, és ezek közül egyszerűségük és alacsony kezdeti költségeik miatt gyakran előnyben részesítik a Trotter-képleteket. Sajnos a Trotter-képletek elméletileg viszonylag pontatlanok újabb és kifinomultabb versenytársaikhoz képest. Bár a több számítási idő segíthet, ez a stratégia gyorsan kezelhetetlenné válik napjaink zajos kvantumeszközein, és korlátozott a hosszú, megszakítás nélküli számítások elvégzésének lehetősége.

A Trotter-szimulációk hibáinak csökkentése érdekében a kvantumfeldolgozási idő növelése nélkül polinomokat használunk a hiba és a lépésméret közötti kapcsolat megismerésére. Különböző lépésméretekre vonatkozó adatok gyűjtésével interpolálhatjuk, azaz befűzhetjük az adatokat egy polinomba, majd megbecsülhetjük a várható viselkedést nagyon kis lépésméretek esetén. Matematikailag bizonyítjuk, hogy megközelítésünk aszimptotikus pontosságjavítást ad a standard Trotterhez képest két alapvető feladat esetében: a sajátértékek becslése és a várható értékek becslése.

Módszerünk egyszerű és praktikus, csak standard technikákat igényel a kvantum és a klasszikus számításokban. Úgy gondoljuk, hogy munkánk erős elméleti támpontot ad az algoritmikus hibacsökkentés további vizsgálataihoz. Ennek a munkának a kiterjesztése több irányba történhet, az elemzésünkben szereplő mesterséges feltételezések kiküszöbölésétől a jobb kvantumszimulációk bemutatásáig.

► BibTeX adatok

@article{Rendon2024javult a pontosság, doi = {10.22331/q-2024-02-26-1266}, url = {https://doi.org/10.22331/q-2024-02-26-1266}, title = {Javított {A}pontosság a {T}rotter {S}imulációkhoz {U}sing {C}hebyshev {I}nterpolation}, szerző = {Rendon, Gumaro és Watkins, Jacob és Wiebe, Nathan}, folyóirat = {{Kvantum}}, issn = {2521-327X}, kiadó = {{Verein zur F{“{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}, kötet = {8}, oldalak = {1266}, hónap = február, év = {2024} }

► Referenciák

[1] S. Lloyd, Univerzális kvantumszimulátorok, Science 273 (1996) 1073.
https:///doi.org/10.1126/science.273.5278.1073

[2] M. Reiher, N. Wiebe, KM Svore, D. Wecker és M. Troyer, Reakciómechanizmusok feltárása kvantumszámítógépeken, Proceedings of the National Academy of Sciences 114 (2017) 7555.
https:///doi.org/10.1073/pnas.161915211

[3] JD Whitfield, J. Biamonte és A. Aspuru-Guzik, Simulation of electronic structure Hamiltonians using quantum computers, Molecular Physics 109 (2011) 735.
https:///doi.org/10.1080/00268976.2011.552441

[4] J. Lee, DW Berry, C. Gidney, WJ Huggins, JR McClean, N. Wiebe és munkatársai, Még hatékonyabb kvantumszámítások kémiáról tenzoros hiperkontrakción keresztül, PRX Quantum 2 (2021) 030305.
https:///doi.org/10.1103/PRXQuantum.2.030305

[5] V. von Burg, GH Low, T. Häner, DS Steiger, M. Reiher, M. Roetteler és munkatársai, Quantum computing enhanced computational catalysis, Physical Review Research 3 (2021) 033055.
https:///doi.org/10.1103/PhysRevResearch.3.033055

[6] SP Jordan, KS Lee és J. Preskill, Quantum algorithms for quantum field theories, Science 336 (2012) 1130.
https:///doi.org/10.1126/science.1217069

[7] AF Shaw, P. Lougovski, JR Stryker és N. Wiebe, Quantum algoritms for simulating the lattice schwinger model, Quantum 4 (2020) 306.
https://doi.org/10.22331/q-2020-08-10-306

[8] N. Klco, MJ Savage és JR Stryker, Su (2) Nem-abeli mérőtérelmélet egy dimenzióban digitális kvantumszámítógépeken, Physical Review D 101 (2020) 074512.
https:///doi.org/10.1103/PhysRevD.101.074512

[9] AM Childs és N. Wiebe, Hamiltoni szimuláció unitárius műveletek lineáris kombinációival, Quantum Info. Comput. 12 (2012) 901–924.
https:///doi.org/10.26421/QIC12.11-12-1

[10] GH Low, V. Kliuchnikov és N. Wiebe, Jól kondicionált többtermékes Hamilton-szimuláció, arXiv:1907.11679 (2019).
https:///doi.org/10.48550/arXiv.1907.11679
arXiv: 1907.11679

[11] DW Berry, AM Childs, R. Cleve, R. Kothari és RD Somma, Hamiltoni dinamika szimulálása csonka taylor sorozattal, Physical review letters 114 (2015) 090502.
https:///doi.org/10.1103/PhysRevLett.114.090502

[12] GH Low és N. Wiebe, Hamiltoni szimuláció az interakciós képben, arXiv:1805.00675 (2018).
https:///doi.org/10.48550/arXiv.1805.00675
arXiv: 1805.00675

[13] M. Kieferová, A. Scherer és DW Berry, Simulating the dynamics of time-dependent hamiltonians with a truncated dyson series, Physical Review A 99 (2019) 042314.
https:///doi.org/10.1103/PhysRevA.99.042314

[14] GH Low és IL Chuang, Hamiltoni szimuláció qubitizációval, Quantum 3 (2019) 163.
https://doi.org/10.22331/q-2019-07-12-163

[15] R. Babbush, C. Gidney, DW Berry, N. Wiebe, J. McClean, A. Paler et al., Encoding electronic spectra in quantum circuits with linear t complexity, Physical Review X 8 (2018) 041015.
https:///doi.org/10.1103/PhysRevX.8.041015

[16] DW Berry, G. Ahokas, R. Cleve és BC Sanders, Hatékony kvantum-algoritmusok ritka hamiltoniak szimulálására, Communications in Mathematical Physics 270 (2006) 359–371.
https:///doi.org/10.1007/s00220-006-0150-x

[17] N. Wiebe, DW Berry, P. Høyer és BC Sanders, Simulating quantum dynamics on a quantum computer, Journal of Physics A: Mathematical and Theoretical 44 (2011) 445308.
https://doi.org/10.1088/1751-8113/44/44/445308

[18] AM Childs, Y. Su, MC Tran, N. Wiebe és S. Zhu, Theory of trotter error with commutator scaling, Physical Review X 11 (2021) 011020.
https:///doi.org/10.1103/PhysRevX.11.011020

[19] J. Haah, MB Hastings, R. Kothari és GH Low, Quantum algorithm for simulating real time evolution of lattice Hamiltonians, SIAM Journal on Computing (2021) FOCS18.
https:///doi.org/10.1137/18M12315

[20] M. Hagan és N. Wiebe, Összetett kvantumszimulációk, arXiv:2206.06409 (2022).
https://doi.org/10.22331/q-2023-11-14-1181
arXiv: 2206.06409

[21] GH Low, Y. Su, Y. Tong és MC Tran, Az ügetőlépések végrehajtásának összetettségéről, arXiv:2211.09133 (2022).
https:///doi.org/10.1103/PRXQuantum.4.020323
arXiv: 2211.09133

[22] GH Low és IL Chuang, Optimális Hamilton-szimuláció kvantumjelfeldolgozással, Physical Review Letters 118 (2017).
https:///doi.org/10.1103/physrevlett.118.010501

[23] S. Endo, Q. Zhao, Y. Li, S. Benjamin és X. Yuan, Mitigating algorithmic errors in a Hamilton-simulation, Phys. Rev. A 99 (2019) 012334.
https:///doi.org/10.1103/PhysRevA.99.012334

[24] AC Vazquez, R. Hiptmair és S. Woerner, Enhancing the quantum linear systems algorithm using richardson extrapolation, ACM Transactions on Quantum Computing 3 (2022).
https:///doi.org/10.1145/3490631

[25] AC Vazquez, DJ Egger, D. Ochsner és S. Woerner, Jól kondicionált többtermékes formulák hardverbarát hamiltoni szimulációhoz, Quantum 7 (2023) 1067.
https://doi.org/10.22331/q-2023-07-25-1067

[26] M. Suzuki: A fraktálút-integrálok általános elmélete soktest-elméletekben és a statisztikai fizikában, Journal of Mathematical Physics 32 (1991) 400.
https:///doi.org/10.1063/1.529425

[27] Gilyén A., Y. Su, GH Low és N. Wiebe, Quantum singular value transformation and after: exponenciális fejlesztések a kvantummátrix aritmetikában, Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, 193–204. , DOI.
https:///doi.org/10.1145/3313276.3316366

[28] C. Yi és E. Crosson, Spectral analysis of product formulas for quantum simulation, npj Quantum Information 8 (2022) 37.
https:///doi.org/10.1038/s41534-022-00548-w

[29] A. Quarteroni, R. Sacco és F. Saleri, Numerical mathematics, vol. 37, Springer Science & Business Media (2010), 10.1007/b98885.
https:///doi.org/10.1007/b98885

[30] F. Piazzon és M. Vianello, Stabilitási egyenlőtlenségek lebesgue állandókhoz markov-szerű egyenlőtlenségek révén, Dolomites Research Notes on Approximation 11 (2018).

[31] AP de Camargo, A lagrange interpoláció Newton-képletének numerikus stabilitásáról, Journal of Computational and Applied Mathematics 365 (2020) 112369.
https:///doi.org/10.1016/j.cam.2019.112369

[32] L. Trefethen, Six myths of polynomial interpolation and quadrature, (2011).

[33] W. Gautschi, Mennyire (nem)stabilak a vandermonde rendszerek? aszimptotikus és számítási elemzés, Lecture Notes in Pure and Applied Mathematics, 193–210. oldal, Marcel Dekker, Inc, 1990.

[34] NJ Higham, The numerical stability of barycentric lagrange interpolation, IMA Journal of Numerical Analysis 24 (2004) 547.
https:///doi.org/10.1093/imanum/24.4.547

[35] JC Mason és DC Handscomb, Chebisev-polinomok, CRC sajtó (2002), 10.1201/9781420036114.
https:///doi.org/10.1201/9781420036114

[36] G. Rendon, T. Izubuchi és Y. Kikuchi, Effects of cosine tapering window on quantum phase estimation, Physical Review D 106 (2022) 034503.
https:///doi.org/10.1103/PhysRevD.106.034503

[37] LN Trefethen, Approximation Theory and Approximation Practice, Extended Edition, SIAM (2019), 10.1137/1.9781611975949.
https:///doi.org/10.1137/1.9781611975949

[38] FL Bauer és CT Fike, Normák és kizárási tételek, Numer. Math. 2 (1960) 137–141.
https:///doi.org/10.1007/BF01386217

[39] S. Blanes, F. Casas, J.-A. Oteo és J. Ros, A magnus expanziója és néhány alkalmazása, Physics jelentések 470 (2009) 151.
https:///doi.org/10.1016/j.physrep.2008.11.001

[40] N. Klco és MJ Savage, Lokalizált hullámfüggvények minimálisan összefonódott állapotú előkészítése kvantumszámítógépeken, Physical Review A 102 (2020).
https:///doi.org/10.1103/physreva.102.012612

[41] JJ García-Ripoll, Kvantum által inspirált algoritmusok többváltozós elemzéshez: az interpolációtól a parciális differenciálegyenletekig, Quantum 5 (2021) 431.
https://doi.org/10.22331/q-2021-04-15-431

[42] W. Górecki, R. Demkowicz-Dobrzański, HM Wiseman és DW Berry, $pi$-korrigált heisenbergi határ, Physical review letters 124 (2020) 030501.
https:///doi.org/10.1103/PhysRevLett.124.030501

[43] D. Grinko, J. Gacon, C. Zoufal és S. Woerner, Iterative quantum amplititude estimation, npj Quantum Information 7 (2021) 52 [1912.05559].
https://doi.org/10.1038/s41534-021-00379-1
arXiv: 1912.05559

[44] N. Wiebe, D. Berry, P. Høyer és BC Sanders, Rendezett operátori exponenciálisok magasabb rendű dekompozíciói, Journal of Physics A: Mathematical and Theoretical 43 (2010) 065203.
https://doi.org/10.1088/1751-8113/43/6/065203

[45] RA Horn és CR Johnson, Mátrix elemzés, Cambridge University Press (2012), 10.1017/CBO9780511810817.
https:///doi.org/10.1017/CBO9780511810817

[46] M. Chiani, D. Dardari és MK Simon, New exponenciális határok és közelítések a fading channels hibavalószínűségének számításához, IEEE Transactions on Wireless Communications 2 (2003) 840.
https:///doi.org/10.1109/TWC.2003.814350

[47] JM Borwein és PB Borwein, Pi és az AGM: egy tanulmány az analitikus számelméletről és a számítási komplexitásról, Wiley-Interscience (1987).

[48] BL Higgins, DW Berry, SD Bartlett, HM Wiseman és GJ Pryde, Entanglement-free Heisenberg-limited phase estimation, Nature 450 (2007) 393.
https:///doi.org/10.1038/nature06257

[49] RB Griffiths és C.-S. Niu, Semiclassical Fourier Transform for Quantum Computation, Physical Review Letters 76 (1996) 3228.
https:///doi.org/10.1103/PhysRevLett.76.3228

[50] AY Kitaev, Kvantummérések és az Abel-stabilizátor probléma, quant-ph/9511026 (1995).
https:///doi.org/10.48550/arXiv.quant-ph/9511026
arXiv:quant-ph/9511026

[51] DS Abrams és S. Lloyd: Kvantum algoritmus, amely exponenciális sebességnövekedést biztosít sajátértékek és sajátvektorok megtalálásához, Physical Review Letters 83 (1999) 5162.
https:///doi.org/10.1103/PhysRevLett.83.5162

[52] J. Watkins, N. Wiebe, A. Roggero és D. Lee, Time-dependent Hamilton-szimuláció diszkrét óraszerkezetekkel, arXiv:2203.11353 (2022).
https:///doi.org/10.48550/arXiv.2203.11353
arXiv: 2203.11353

[53] TD Ahle, Éles és egyszerű korlátok a binomiális és Poisson eloszlás nyers momentumaihoz, Statistics & Probability Letters 182 (2022) 109306.
https:///doi.org/10.1016/j.spl.2021.109306

[54] T. Rivlin, Chebyshev Polynomials, Dover Books on Mathematics, Dover Publications (2020).

Idézi

[1] Dean Lee, „Kvantumtechnikák sajátérték-problémákhoz”, European Physical Journal A 59 11, 275 (2023).

[2] Tatsuhiko N. Ikeda, Hideki Kono és Keisuke Fujii, „Trotter24: A precíziós garantált adaptív lépcsõméretû trotterizáció Hamilton-szimulációkhoz”, arXiv: 2307.05406, (2023).

[3] Hans Hon Sang Chan, Richard Meister, Matthew L. Goh és Koczor Bálint, „Algoritmikus árnyékspektroszkópia”, arXiv: 2212.11036, (2022).

[4] Sergiy Zhuk, Niall Robertson és Sergey Bravyi, „Trotter hibahatárok és dinamikus többtermékes képletek a Hamilton-szimulációhoz”, arXiv: 2306.12569, (2023).

[5] Zhicheng Zhang, Qisheng Wang és Mingsheng Ying, „Parallel Quantum Algorithm for Hamiltonan Simulation”, Quantum 8, 1228 (2024).

[6] Lea M. Trenkwalder, Eleanor Scerri, Thomas E. O'Brien és Vedran Dunjko, „Hamiltoni termék-képlet összeállítása megerősítéses tanulás révén”, arXiv: 2311.04285, (2023).

[7] Gumaro Rendon és Peter D. Johnson, „Low-depth Gaussian State Energy Estimation”, arXiv: 2309.16790, (2023).

[8] Gregory Boyd, „Low-Overhead Parallelisation of LCU via Commuting Operators”, arXiv: 2312.00696, (2023).

A fenti idézetek innen származnak SAO/NASA HIRDETÉSEK (utolsó sikeres frissítés: 2024-02-27 02:40:25). Előfordulhat, hogy a lista hiányos, mivel nem minden kiadó ad megfelelő és teljes hivatkozási adatokat.

On Crossref által idézett szolgáltatás művekre hivatkozó adat nem található (utolsó próbálkozás 2024-02-27 02:40:24).

Ez a tanulmány a Quantumban jelent meg Creative Commons Nevezd meg 4.0 International (CC BY 4.0) engedély. A szerzői jog az eredeti szerzői jog tulajdonosainál marad, például a szerzőknél vagy intézményeiknél.

SEO által támogatott tartalom és PR terjesztés. Erősödjön még ma.
PlatoData.Network Vertical Generative Ai. Erősítse meg magát. Hozzáférés itt.
PlatoAiStream. Web3 Intelligence. Felerősített tudás. Hozzáférés itt.
PlatoESG. Carbon, CleanTech, Energia, Környezet, Nap, Hulladékgazdálkodás. Hozzáférés itt.
PlatoHealth. Biotechnológiai és klinikai vizsgálatok intelligencia. Hozzáférés itt.
Forrás: https://quantum-journal.org/papers/q-2024-02-26-1266/

Időbélyeg: Február 26, 2024

Időbélyeg: 20. október 2022.

Gyors Black-Box kvantumállapot-előkészítés

Forrás klaszter:

Quantum Journal

Forrás csomópont: 1607653

Időbélyeg: 4. augusztus 2022.

Megnövelt pontosság az ügetőszimulációkhoz Csebisev-interpoláció segítségével

Újra kiadta Platón

Absztrakt

Népszerű összefoglaló

► BibTeX adatok

► Referenciák

Idézi

Még több Quantum Journal

Modell prediktív vezérlés robusztus kvantumállapot-előkészítéshez

Helyezze el a hozzáférést a Surface Code Y bázishoz

Kvantumadatok kovácsolása: klasszikusan az IQP-alapú kvantumteszt legyőzése

Kvantum helyi keresés az Ansatz kvantum váltakozó operátorral

Összegabalyodással továbbfejlesztett tesztjavaslat lokális Lorentz-szimmetria megsértésére spinor atomokon keresztül

Összefonódási entrópia előállítása kvantumneurális hálózatokban

Folyékony fermionos töredékek az elektronikus Hamiltonok kvantummérésének optimalizálásához a variációs kvantum-sajátmegoldóban

Hamiltoni variációs ansatz meddő fennsíkok nélkül

Helyi rejtett változóértékek optimalizálási eljárások nélkül

Egyszerű és praktikus DIQKD biztonsági elemzés BB84 típusú bizonytalansági relációk és Pauli korrelációs megszorítások segítségével

Gyors Black-Box kvantumállapot-előkészítés

Rólunk

Vertical Search & Ai

Emelvény

Maradjon kapcsolatban

Fiók