Hypergraphs Mengungkapkan Solusi untuk Masalah 50 Tahun

Dalam 1850, Thomas Penyington Kirkman, seorang ahli matematika ketika dia tidak memenuhi tanggung jawab utamanya sebagai vikaris di Gereja Inggris, menggambarkan "masalah anak sekolahnya": "Lima belas wanita muda di sebuah sekolah keluar tiga kali berturut-turut selama tujuh hari berturut-turut: diperlukan untuk mengatur mereka setiap hari, supaya tidak ada dua orang yang berjalan dua kali berturut-turut.”

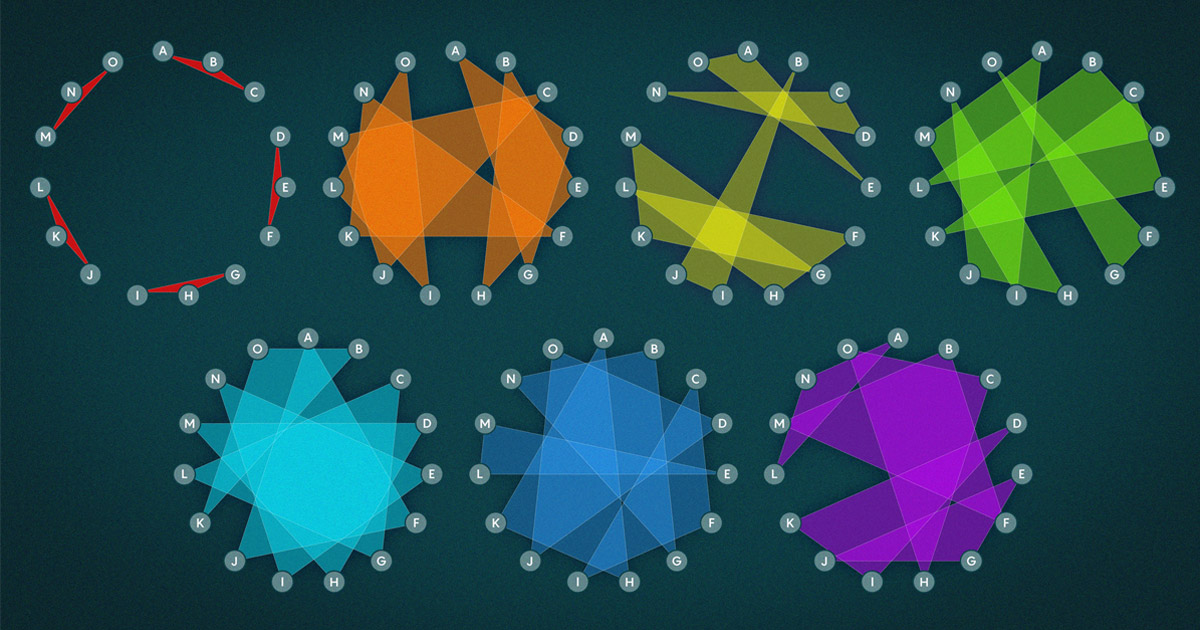
Untuk matematikawan modern, masalah semacam ini paling baik dibayangkan sebagai hipergraf - satu set node yang dikumpulkan dalam kelompok tiga atau lebih. 15 siswi adalah simpul, dan setiap kelompok "tiga sejajar" dapat dianggap sebagai segitiga, dengan tiga garis, atau tepi, menghubungkan tiga simpul.

Masalah Kirkman pada dasarnya menanyakan apakah ada susunan segitiga yang menghubungkan semua siswi satu sama lain, tetapi dengan batasan tambahan bahwa tidak ada dua segitiga yang berbagi sisi. Berbagi tepi akan menyiratkan bahwa dua siswi harus berjalan bersama lebih dari sekali. Pembatasan ini berarti setiap gadis berjalan dengan dua teman baru setiap hari selama seminggu, sehingga setiap pasangan yang mungkin berkumpul tepat satu kali.

Masalah ini dan masalah lain seperti itu telah menipu para matematikawan selama hampir dua abad sejak Kirkman mengajukan pertanyaannya. Pada tahun 1973, matematikawan legendaris Paul Erdős berpose serupa. Dia bertanya apakah mungkin untuk membangun hypergraph dengan dua properti yang tampaknya tidak kompatibel. Pertama, setiap pasang simpul harus dihubungkan oleh tepat satu segitiga, seperti pada siswi. Properti ini membuat grafik padat dengan segitiga. Persyaratan kedua memaksa segitiga untuk menyebar dengan cara yang sangat tepat. (Secara khusus, ini mensyaratkan bahwa untuk setiap kelompok segitiga kecil, setidaknya ada tiga simpul lebih banyak daripada segitiga.) "Anda memiliki perilaku yang sedikit kontradiktif ini di mana Anda memiliki objek keseluruhan padat yang tidak memiliki bagian padat," kata David Conlon, seorang ahli matematika di California Institute of Technology.

Januari ini, di bukti 50 halaman yang rumit, empat ahli matematika membuktikan bahwa selalu mungkin untuk membangun hipergraf seperti itu selama Anda memiliki cukup simpul. “Jumlah teknis yang [mereka] lalui, hanya untuk mendapatkan ini, itu luar biasa,” kata Alan Lo, seorang matematikawan di University of Birmingham. Conlon sependapat: "Ini adalah karya yang sangat mengesankan."

Tim peneliti membangun sistem yang memenuhi persyaratan jahat Erdős dengan memulai proses acak untuk memilih segitiga dan merekayasanya dengan sangat hati-hati agar sesuai dengan kebutuhan mereka. “Jumlah modifikasi sulit yang masuk ke pembuktian sebenarnya agak mengejutkan,” kata Conlon.

Strategi mereka adalah dengan hati-hati membangun hypergraph dari segitiga individu. Misalnya, bayangkan 15 siswi kita. Tarik garis di antara setiap pasangan.

Tujuannya di sini adalah untuk melacak segitiga di atas garis-garis ini sehingga segitiga memenuhi dua persyaratan: Pertama, tidak ada dua segitiga yang berbagi sisi. (Sistem yang memenuhi persyaratan ini disebut sistem triple Steiner.) Dan kedua, pastikan bahwa setiap subset kecil dari segitiga menggunakan jumlah node yang cukup besar.

Cara para peneliti melakukan ini mungkin paling baik dipahami dengan sebuah analogi.

Katakan bahwa alih-alih membuat segitiga dari tepi, Anda sedang membangun rumah dari batu bata Lego. Beberapa bangunan pertama yang Anda buat sangat mewah, dengan perkuatan struktural dan ornamen yang rumit. Setelah Anda selesai dengan ini, sisihkan. Mereka akan berfungsi sebagai "penyerap" - semacam stockpile terstruktur.

Sekarang mulailah membuat bangunan dari batu bata yang tersisa, lanjutkan tanpa banyak perencanaan. Ketika persediaan Lego Anda berkurang, Anda mungkin menemukan beberapa batu bata liar, atau rumah yang secara struktural tidak sehat. Tetapi karena bangunan penyerap terlalu berlebihan dan diperkuat, Anda dapat memetik beberapa batu bata di sana-sini dan menggunakannya tanpa menimbulkan bencana.

Dalam kasus sistem triple Steiner, Anda mencoba membuat segitiga. Penyerap Anda, dalam hal ini, adalah kumpulan tepi yang dipilih dengan cermat. Jika Anda tidak dapat menyortir sisa sistem menjadi segitiga, Anda dapat menggunakan beberapa tepi yang mengarah ke penyerap. Kemudian, setelah selesai melakukannya, Anda memecah penyerap itu sendiri menjadi segitiga.

Penyerapan tidak selalu berhasil. Tapi matematikawan telah mengutak-atik prosesnya, menemukan cara baru untuk mengatasi rintangan. Misalnya, varian kuat yang disebut penyerapan iteratif membagi tepi menjadi urutan set bersarang, sehingga masing-masing bertindak sebagai penyerap untuk yang terbesar berikutnya.

“Selama dekade terakhir ini ada perbaikan besar-besaran,” kata Conlon. “Ini adalah bentuk seni, tetapi mereka benar-benar membawanya ke tingkat seni yang tinggi pada saat ini.”

Masalah Erdős rumit bahkan dengan penyerapan berulang. "Menjadi cukup jelas dengan cepat mengapa masalah ini tidak diselesaikan," kata Mehtaab Sawhney, salah satu dari empat peneliti yang memecahkannya, bersama dengan Ashwin Sahu, yang bersama dengan Sawhney adalah mahasiswa pascasarjana di Massachusetts Institute of Technology;  Michael Simkin, seorang rekan postdoctoral di Pusat Ilmu dan Aplikasi Matematika di Universitas Harvard; dan Matius Kwan, seorang ahli matematika di Institut Sains dan Teknologi Austria. "Ada tugas teknis yang cukup menarik dan cukup sulit."

Misalnya, dalam aplikasi lain dari penyerapan berulang, setelah Anda selesai menutupi satu set — baik dengan segitiga, untuk sistem triple Steiner, atau dengan struktur lain untuk masalah lain — Anda dapat mempertimbangkan untuk menanganinya dan melupakannya. Kondisi Erdős, bagaimanapun, mencegah keempat matematikawan melakukan itu. Sekelompok segitiga yang bermasalah dapat dengan mudah melibatkan simpul dari beberapa set penyerap.

“Segitiga yang Anda pilih 500 langkah yang lalu, Anda harus ingat bagaimana memikirkannya,” kata Sawhney.

Apa yang akhirnya diketahui keempatnya adalah bahwa jika mereka memilih segitiga mereka dengan hati-hati, mereka dapat menghindari kebutuhan untuk melacak setiap hal kecil. “Apa yang lebih baik untuk dilakukan adalah memikirkan himpunan kecil 100 segitiga dan menjamin bahwa himpunan segitiga dipilih dengan probabilitas yang benar,” kata Sawhney.

Penulis makalah baru ini optimis bahwa teknik mereka dapat diperluas melampaui masalah yang satu ini. Mereka punya sudah menerapkan strategi mereka untuk masalah tentang kotak latin, yang seperti penyederhanaan teka-teki sudoku.

Di luar itu, ada beberapa pertanyaan yang pada akhirnya bisa mengarah pada metode penyerapan, kata Kwan. “Ada begitu banyak masalah dalam kombinatorik, terutama dalam teori desain, di mana proses acak adalah alat yang sangat ampuh.” Salah satu masalah tersebut, dugaan Ryser-Brualdi-Stein, juga tentang kuadrat Latin dan telah menunggu solusi sejak tahun 1960-an.

Meskipun penyerapan mungkin perlu pengembangan lebih lanjut sebelum dapat mengatasi masalah itu, ia telah melalui perjalanan panjang sejak dimulai 30 lalu, kata Maya Stein, wakil direktur Pusat Pemodelan Matematika di Universitas Chili. “Itu adalah sesuatu yang sangat bagus untuk dilihat, bagaimana metode ini berkembang.”