I "mormorii" della curva ellittica trovati con l'intelligenza artificiale prendono il volo | Rivista Quanti

Le curve ellittiche sono tra gli oggetti più affascinanti della matematica moderna. Non sembrano complicati, ma costituiscono una superstrada tra la matematica che molte persone imparano al liceo e la ricerca matematica nella sua forma più astrusa. Furono fondamentali per la celebre dimostrazione dell'Ultimo Teorema di Fermat di Andrew Wiles negli anni '1990. Sono strumenti chiave nella crittografia moderna. E nel 2000, il Clay Mathematics Institute ha nominato a congetture sulle statistiche delle curve ellittiche è uno dei sette “Problemi da Premio del Millennio”, ciascuno dei quali prevede un premio di 1 milione di dollari per la sua soluzione. Quella congettura, azzardata per la prima volta da Bryan Birch ed Peter Swinnerton-Dyer negli anni '1960, non è ancora stato dimostrato.

Comprendere le curve ellittiche è un'impresa ad alto rischio che è stata fondamentale per la matematica. Quindi nel 2022, quando una collaborazione transatlantica ha utilizzato tecniche statistiche e intelligenza artificiale per scoprire modelli completamente inaspettati nelle curve ellittiche, è stato un contributo gradito, anche se inaspettato. "Era solo questione di tempo prima che il machine learning arrivasse alla nostra porta con qualcosa di interessante", ha detto Pietro Sarnaki, matematico presso l'Institute for Advanced Study e l'Università di Princeton. Inizialmente, nessuno poteva spiegare il motivo per cui esistono i modelli appena scoperti. Da allora, in una serie di articoli recenti, i matematici hanno iniziato a svelare le ragioni dietro questi schemi, soprannominati “mormorazioni” per la loro somiglianza con le forme fluide degli storni in stormo, e hanno iniziato a dimostrare che devono verificarsi non solo in particolari esempi esaminati nel 2022, ma più in generale in curve ellittiche.

L'importanza di essere ellittici

Per capire quali sono questi schemi, dobbiamo gettare le basi su cosa sono le curve ellittiche e su come le classificano i matematici.

Una curva ellittica mette in relazione il quadrato di una variabile, comunemente scritta come y, alla terza potenza di un altro, comunemente scritto come x: y² = x³ + Ax + B, per qualche coppia di numeri A ed B, Purché A ed B soddisfare alcune semplici condizioni. Questa equazione definisce una curva che può essere rappresentata graficamente sul piano, come mostrato di seguito. (Nonostante la somiglianza nei nomi, un'ellisse non è una curva ellittica.)

Sebbene sembrino semplici, le curve ellittiche si rivelano strumenti incredibilmente potenti per i teorici dei numeri, i matematici che cercano modelli negli interi. Invece di lasciare che le variabili x ed y spaziano su tutti i numeri, ai matematici piace restringerli a diversi sistemi numerici, cosa che chiamano definizione di una curva “sopra” un dato sistema numerico. Le curve ellittiche limitate ai numeri razionali – numeri che possono essere scritti come frazioni – sono particolarmente utili. "Le curve ellittiche sui numeri reali o complessi sono piuttosto noiose", ha detto Sarnak. “Solo i numeri razionali sono profondi.”

Ecco un modo in cui è vero. Se tracciamo una linea retta tra due punti razionali su una curva ellittica, anche il punto in cui quella linea interseca nuovamente la curva sarà razionale. Puoi usare questo fatto per definire la "addizione" in una curva ellittica, come mostrato di seguito.

Traccia una linea in mezzo P ed Q. Quella linea intersecherà la curva in un terzo punto, R. (I matematici hanno un trucco speciale per affrontare il caso in cui la linea non interseca la curva aggiungendo un "punto all'infinito".) R attraverso l' x-axis è la tua somma P + Q. Insieme a questa operazione di addizione, tutte le soluzioni della curva formano un oggetto matematico chiamato gruppo.

I matematici lo usano per definire il “rango” di una curva. IL rango di una curva si riferisce al numero di soluzioni razionali che ha. Le curve di rango 0 hanno un numero finito di soluzioni. Le curve con rango più alto hanno un numero infinito di soluzioni la cui relazione tra loro utilizzando l'operazione di addizione è descritta dal rango.

I gradi non sono ben compresi; i matematici non sempre hanno un modo per calcolarli e non sanno quanto possono diventare grandi. (Il rango esatto più grande noto per una curva specifica è 20.) Curve dall'aspetto simile possono avere ranghi completamente diversi.

Le curve ellittiche hanno molto a che fare anche con i numeri primi, che sono divisibili solo per 1 e per se stessi. In particolare, i matematici osservano le curve su campi finiti, sistemi di aritmetica ciclica definiti per ciascun numero primo. Un campo finito è come un orologio con il numero di ore uguale al numero primo: se continui a contare verso l'alto, i numeri ricominciano da capo. Nel campo finito per 7, ad esempio, 5 più 2 è uguale a zero e 5 più 3 è uguale a 1.

Ad una curva ellittica è associata una sequenza di numeri, chiamata a_p, che si riferisce al numero di soluzioni della curva nel campo finito definito dal numero primo p. Un più piccolo a_p significa più soluzioni; uno più grande a_p significa meno soluzioni. Sebbene il rango sia difficile da calcolare, la sequenza a_p è molto più semplice.

Sulla base di numerosi calcoli effettuati su uno dei primissimi computer, Birch e Swinnerton-Dyer ipotizzarono una relazione tra il rango di una curva ellittica e la sequenza a_p. Chiunque possa dimostrare di avere ragione può vincere un milione di dollari e l’immortalità matematica.

Emerge uno schema a sorpresa

Dopo l’inizio della pandemia, Yang-Hui He, ricercatore presso il London Institute for Mathematical Sciences, ha deciso di affrontare alcune nuove sfide. Si era laureato in fisica al college e aveva conseguito il dottorato in fisica matematica al Massachusetts Institute of Technology. Ma era sempre più interessato alla teoria dei numeri e, date le crescenti capacità dell'intelligenza artificiale, pensò di provare a usare l'intelligenza artificiale come strumento per trovare schemi inaspettati nei numeri. (Lo era già stato utilizzando l'apprendimento automatico classificare Varietà di Calabi-Yau, strutture matematiche ampiamente utilizzate nella teoria delle stringhe.)

Nell'agosto 2020, con l'aggravarsi della pandemia, l'Università di Nottingham lo ha ospitato per un anno parlare in linea. Era pessimista sui suoi progressi e sulla possibilità stessa di utilizzare l’apprendimento automatico per scoprire nuova matematica. "La sua narrazione era che la teoria dei numeri era difficile perché non si potevano imparare le cose dalla teoria dei numeri", ha detto Thomas oliver, un matematico dell'Università di Westminster che era tra il pubblico. Come ricorda, “non sono riuscito a trovare nulla perché non ero un esperto. Non stavo nemmeno usando le cose giuste per guardarlo.

Oliver e Kyu-Hwan Lee, matematico dell'Università del Connecticut, iniziò a lavorare con He. "Abbiamo deciso di farlo solo per imparare cosa fosse l'apprendimento automatico, piuttosto che per studiare seriamente la matematica", ha detto Oliver. "Ma abbiamo subito scoperto che è possibile apprendere automaticamente molte cose."

Oliver e Lee gli suggerirono di applicare le sue tecniche per esaminare L-funzioni, serie infinite strettamente legate alle curve ellittiche attraverso la sequenza a_p. Potrebbero utilizzare un database online di curve ellittiche e relative L-funzioni chiamate LMFDB per addestrare i propri classificatori di machine learning. All'epoca il database conteneva poco più di 3 milioni di curve ellittiche rispetto alle razionali. Entro ottobre 2020, lo avevano fatto un documento da cui hanno utilizzato le informazioni raccolte L-funzioni per prevedere una particolare proprietà delle curve ellittiche. A novembre hanno condiviso un altro documento che utilizzava l’apprendimento automatico per classificare altri oggetti nella teoria dei numeri. A dicembre furono in grado di farlo prevedere i ranghi delle curve ellittiche con elevata precisione.

Ma non erano sicuri del motivo per cui i loro algoritmi di apprendimento automatico funzionassero così bene. Lee ha chiesto al suo studente universitario Alexey Pozdnyakov di vedere se riusciva a capire cosa stava succedendo. In realtà, l'LMFDB ordina le curve ellittiche in base a una quantità chiamata conduttore, che riassume le informazioni sui numeri primi per i quali una curva non si comporta bene. Quindi Pozdnyakov provò a osservare simultaneamente un gran numero di curve con conduttori simili: diciamo, tutte le curve con conduttori tra 7,500 e 10,000.

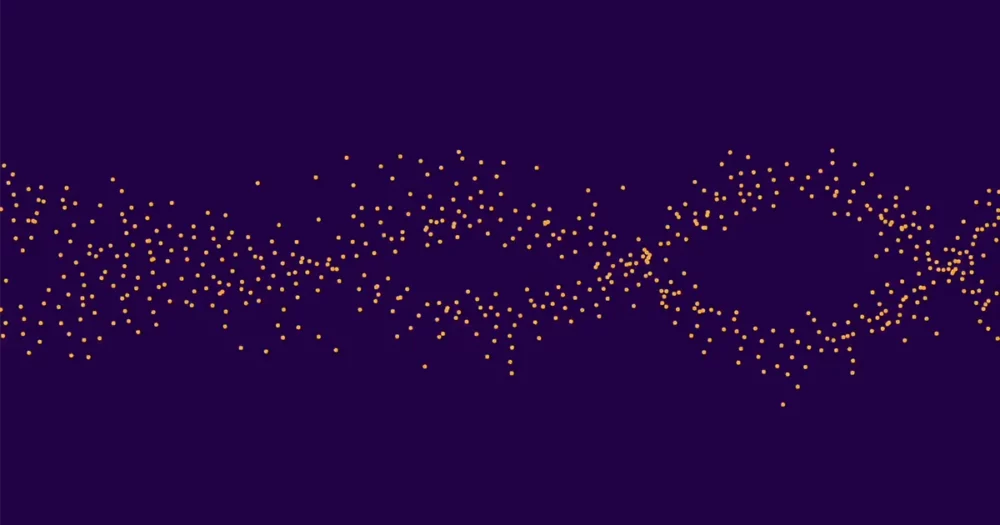
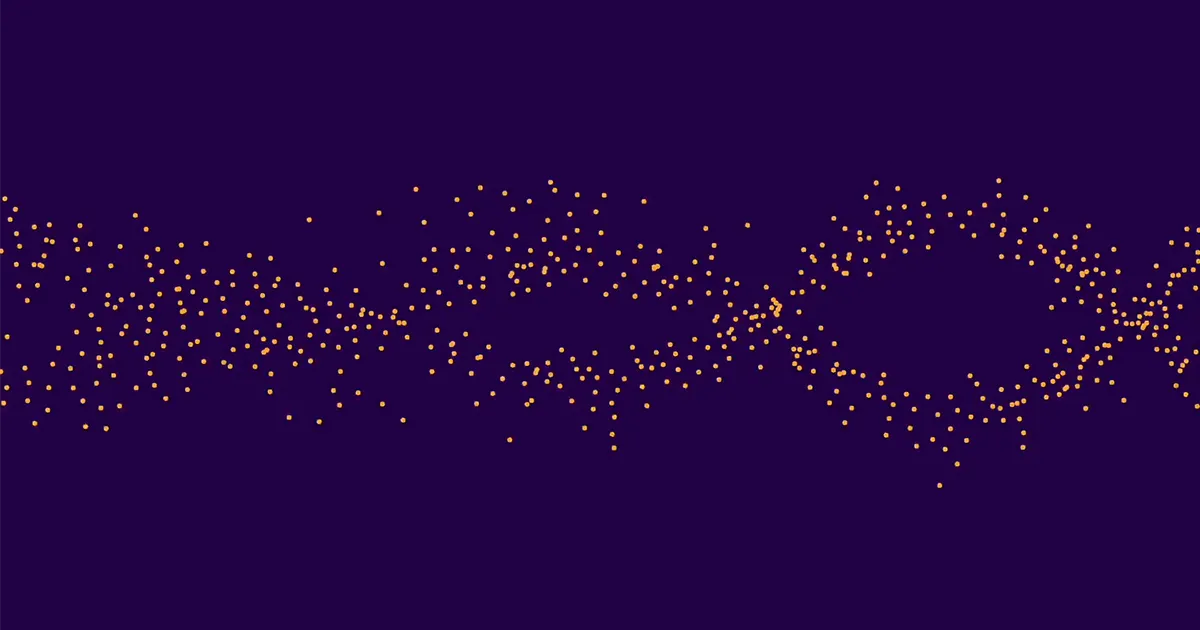
In totale si tratta di circa 10,000 curve. Circa la metà di questi aveva rango 0 e metà rango 1. (I ranghi più alti sono estremamente rari). Ha poi calcolato la media dei valori di a_p per tutte le curve di rango 0, media separata a_p per tutte le curve di rango 1 e abbiamo tracciato i risultati. Le due serie di punti formavano due onde distinte e facilmente distinguibili. Questo è il motivo per cui i classificatori basati sull’apprendimento automatico sono stati in grado di accertare correttamente i ranghi di particolari curve.

"All'inizio ero semplicemente felice di aver completato l'incarico", ha detto Pozdnyakov. "Ma Kyu-Hwan ha immediatamente riconosciuto che questo schema era sorprendente, ed è stato allora che è diventato davvero emozionante."

Lee e Oliver erano affascinati. "Alexey ci ha mostrato la foto e ho detto che assomiglia a quella cosa che fanno gli uccelli", ha detto Oliver. "E poi Kyu-Hwan ha cercato e ha detto che si chiama mormorio, e poi Yang ha detto che dovremmo chiamare il giornale 'Mormorii di curve ellittiche. '”

Hanno caricato il loro articolo nell’aprile 2022 e lo hanno inoltrato a una manciata di altri matematici, aspettandosi nervosamente di sentirsi dire che la loro cosiddetta “scoperta” era ben nota. Oliver ha detto che la relazione era così visibile che avrebbe dovuto essere notata molto tempo fa.

Quasi immediatamente, la prestampa ha suscitato interesse, in particolare da parte di Andrea Sutherland, ricercatore del MIT e uno dei caporedattori di LMFDB. Sutherland si rese conto che 3 milioni di curve ellittiche non erano sufficienti per i suoi scopi. Voleva esaminare gamme di conduttori molto più ampie per vedere quanto fossero robusti i mormorii. Ha estratto dati da un altro immenso archivio di circa 150 milioni di curve ellittiche. Ancora insoddisfatto, estrasse i dati da un archivio diverso con 300 milioni di curve.

"Ma anche quelli non erano sufficienti, quindi ho effettivamente calcolato un nuovo set di dati di oltre un miliardo di curve ellittiche, ed è quello che ho usato per calcolare le immagini ad alta risoluzione", ha detto Sutherland. I mormorii emergevano sia che avesse una media di oltre 15,000 curve ellittiche alla volta o di un milione alla volta. La forma rimaneva la stessa anche quando osservava le curve su numeri primi sempre più grandi, un fenomeno chiamato invarianza di scala. Sutherland si rese conto anche che i mormorii non sono esclusivi delle curve ellittiche, ma compaiono anche in modo più generale L-funzioni. Ha scritto una lettera che riassume le sue scoperte e lo inviò a Sarnak e Michele Rubinstein presso l'Università di Waterloo.

"Se c'è una spiegazione nota, mi aspetto che lo saprai", ha scritto Sutherland.

Non l'hanno fatto.

Spiegare il modello

Lee, He e Oliver hanno organizzato un seminario sulle mormorazioni nell'agosto 2023 presso l'Istituto per la ricerca computazionale e sperimentale in matematica (ICERM) della Brown University. Vennero Sarnak e Rubinstein, così come lo studente di Sarnak Nina Zubrilina.

Zubrilina ha presentato la sua ricerca sui modelli di mormorio in forme modulari, funzioni complesse speciali che, come le curve ellittiche, sono associate L-funzioni. Nelle forme modulari con conduttori di grandi dimensioni, i mormorii convergono in una curva nettamente definita, anziché formare uno schema distinguibile ma disperso. In un documento pubblicato l'11 ottobre 2023, Zubrilina ha dimostrato che questo tipo di mormorio segue una formula esplicita da lei scoperta.

“Il grande risultato di Nina è quello di aver dato una formula per questo; Io la chiamo la formula della densità di mormorazione di Zubrilina”, ha detto Sarnak. "Utilizzando calcoli molto sofisticati, ha dimostrato una formula esatta che si adatta perfettamente ai dati."

La sua formula è complicata, ma Sarnak la considera un nuovo importante tipo di funzione, paragonabile alle funzioni di Airy che definiscono soluzioni alle equazioni differenziali utilizzate in una varietà di contesti fisici, dall'ottica alla meccanica quantistica.

Sebbene la formula di Zubrilina sia stata la prima, ne sono seguite altre. "Ogni settimana ormai esce un nuovo articolo", ha detto Sarnak, "utilizzando principalmente gli strumenti di Zubrilina, che spiega altri aspetti delle mormorazioni".

Jonathan Bober, Andrea Booker ed Min lee dell'Università di Bristol, insieme a David Lowry-Duda dell'ICERM, ha dimostrato l'esistenza di un diverso tipo di murmurazione nelle forme modulari in un altro articolo di ottobre. E Kyu-Hwan Lee, Oliver e Pozdnyakov ne dimostrò l'esistenza di mormorii in oggetti chiamati personaggi di Dirichlet a cui sono strettamente imparentati L-funzioni.

Sutherland rimase impressionato dalla significativa dose di fortuna che aveva portato alla scoperta dei mormorii. Se i dati della curva ellittica non fossero stati ordinati per conduttore, i mormorii sarebbero scomparsi. "Hanno avuto la fortuna di prendere i dati dal LMFDB, che sono stati preordinati in base al conduttore", ha detto. “È ciò che mette in relazione una curva ellittica con la corrispondente forma modulare, ma questo non è affatto ovvio. … Due curve le cui equazioni sembrano molto simili possono avere conduttori molto diversi.” Ad esempio, Sutherland lo ha notato y² = x³ - 11x + 6 ha il conduttore 17, ma trasformando il segno meno in segno più, y² = x³ + 11x + 6 ha conduttore 100,736.

Anche allora le mormorazioni furono riscontrate solo a causa dell'inesperienza di Pozdnjakov. “Non penso che l'avremmo trovato senza di lui”, ha detto Oliver, “perché gli esperti tradizionalmente normalizzano a_p avere valore assoluto 1. Ma non li ha normalizzati… quindi le oscillazioni erano molto grandi e visibili.”

I modelli statistici che gli algoritmi di intelligenza artificiale utilizzano per ordinare le curve ellittiche in base al rango esistono in uno spazio parametrico con centinaia di dimensioni: troppe perché le persone possano ordinarle nella loro mente, per non parlare di visualizzarle, ha osservato Oliver. Ma sebbene l’apprendimento automatico abbia scoperto le oscillazioni nascoste, “solo più tardi abbiamo capito che si trattava di mormorii”.

Nota dell'editore: Andrew Sutherland, Kyu-Hwan Lee e il database delle funzioni L e dei moduli modulari (LMFDB) hanno tutti ricevuto finanziamenti dalla Simons Foundation, che finanzia anche questa pubblicazione editorialmente indipendente. Le decisioni di finanziamento della Simons Foundation non hanno alcuna influenza sulla nostra copertura. Sono disponibili ulteriori informazioni qui.