I matematici lanciano i dadi e ottengono sasso-carta-forbici

Mentre Bill Gates racconta la storia, Warren Buffett una volta lo sfidò a una partita a dadi. Ciascuno selezionerebbe uno dei quattro dadi appartenenti a Buffett, e poi tirerebbe, con il numero più alto vincente. Questi non erano dadi standard: avevano un diverso assortimento di numeri rispetto ai soliti da 1 a 6. Buffett si offrì di lasciare che Gates scegliesse per primo, in modo che potesse scegliere il dado più forte. Ma dopo che Gates ha esaminato i dadi, ha restituito una controproposta: Buffett dovrebbe scegliere per primo.

Gates aveva riconosciuto che i dadi di Buffett esibivano una proprietà curiosa: nessuno di loro era il più forte. Se Gates avesse scelto per primo, qualunque dado avesse scelto, Buffett sarebbe stato in grado di trovare un altro dado che potesse batterlo (cioè uno con più del 50% di possibilità di vincere).

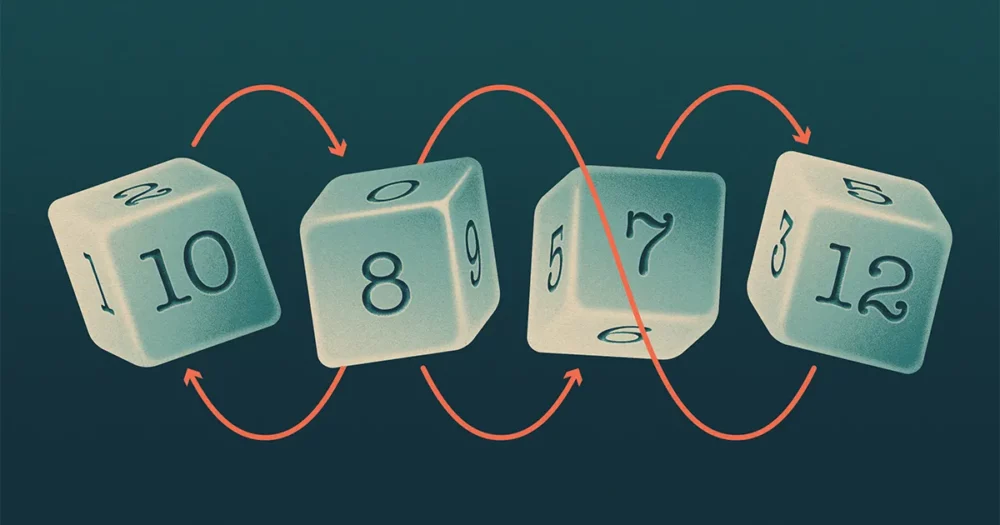
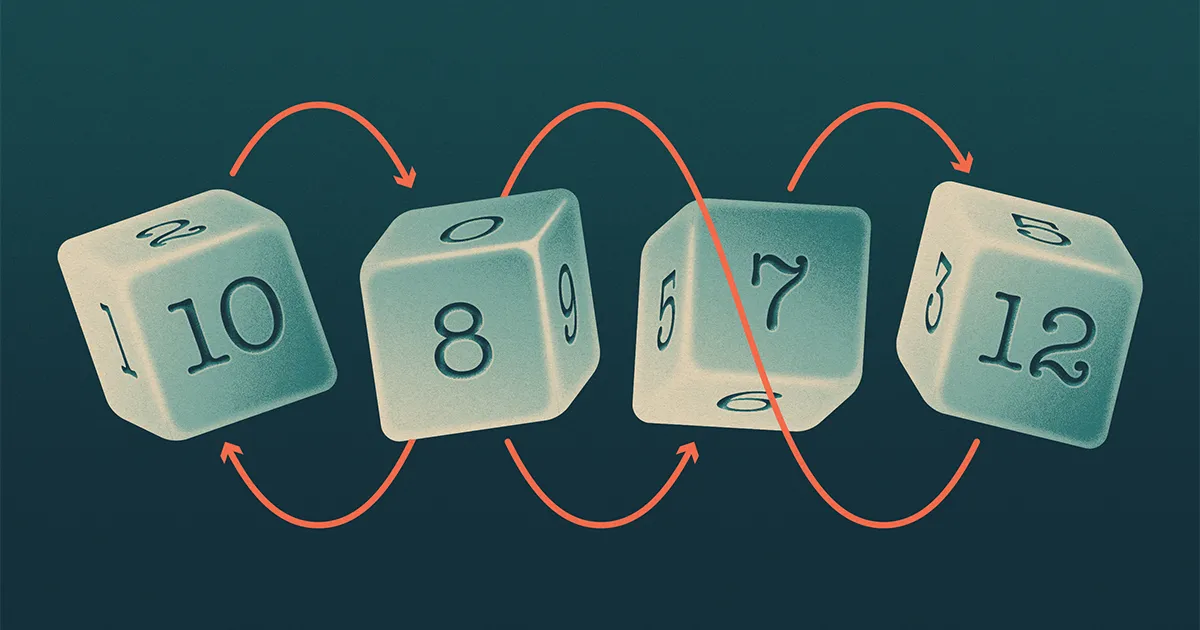
I quattro dadi di Buffett (chiamateli A, B, C ed D) formava uno schema che ricordava sasso-carta-forbici, in cui A battiti B, B battiti C, C battiti D ed D battiti A. I matematici dicono che un tale set di dadi è "intransitivo".

"Non è affatto intuitivo che [i dadi intransitivi] debbano esistere", ha detto Brian Conrey, il direttore dell'American Institute of Mathematics (AIM) di San Jose, che ha scritto un articolo influente sull'argomento nel 2013.

I matematici hanno inventato il primi esempi di dadi intransitivi più di 50 anni fa, e alla fine dimostrato che considerando dadi con sempre più facce, è possibile creare cicli intransitivi di qualsiasi lunghezza. Ciò che i matematici non sapevano fino a poco tempo fa era quanto siano comuni i dadi intransitivi. Devi escogitare attentamente tali esempi o puoi scegliere i dadi a caso e avere una buona possibilità di trovare un insieme intransitivo?

Guardando tre dadi, se lo sai A battiti B ed B battiti C, sembra una prova che A è il più forte; situazioni dove C battiti A dovrebbe essere raro. E in effetti, se i numeri sui dadi possono sommarsi a totali diversi, allora i matematici credono che questa intuizione sia vera.

Ma a documento pubblicato online alla fine dell'anno scorso dimostra che in un altro contesto naturale, questa intuizione fallisce in modo spettacolare. Supponiamo che tu richieda che i tuoi dadi utilizzino solo i numeri che appaiono su un normale dado e abbiano lo stesso totale di un normale dado. Quindi, il giornale ha mostrato, se A battiti B ed B battiti C, A ed C hanno sostanzialmente uguali possibilità di prevalere l'uno contro l'altro.

"Sapendo che A battiti B ed B battiti C non ti dà informazioni sul fatto che A battiti C," disse Timothy Gowers dell'Università di Cambridge, medaglia Fields e uno dei contributori al nuovo risultato, che è stato dimostrato tramite una collaborazione online aperta nota come progetto Polymath.

Intanto un altro carta recente analizza serie di quattro o più dadi. Questa scoperta è probabilmente ancora più paradossale: se, per esempio, prendi quattro dadi a caso e scopri che A battiti B, B battiti C ed C battiti D, quindi è leggermente Scopri di più probabilmente per D battere A che il contrario.

Né forte né debole

La recente ondata di risultati è iniziata circa un decennio fa, dopo che Conrey ha partecipato a un raduno per insegnanti di matematica con una sessione che copriva i dadi intransitivi. "Non avevo idea che cose del genere potessero esistere", ha detto. "Sono rimasto affascinato da loro."

Decise (successivamente affiancato dal suo collega Ken Morrison all'AIM) per esplorare l'argomento con tre studenti delle scuole superiori di cui faceva da mentore: James Gabbard, Katie Grant e Andrew Liu. Quante volte, si chiedeva il gruppo, i dadi scelti a caso formeranno un ciclo intransitivo?

Si ritiene che i set di dadi intransitivi siano rari se i numeri delle facce dei dadi si sommano a totali diversi, poiché è probabile che il dado con il totale più alto batta gli altri. Quindi il team ha deciso di concentrarsi su dadi che hanno due proprietà: in primo luogo, i dadi usano gli stessi numeri di un dado standard, da 1 a n, nel caso di un ndado a due facce. E in secondo luogo, i numeri delle facce si sommano allo stesso totale di un dado standard. Ma a differenza dei dadi standard, ogni dado può ripetere alcuni numeri e tralasciarne altri.

Nel caso dei dadi a sei facce, ci sono solo 32 dadi diversi che hanno queste due proprietà. Quindi, con l'aiuto di un computer, il team ha potuto identificare tutte le triple in cui A battiti B ed B battiti C. I ricercatori hanno scoperto, con loro stupore, che A battiti C in 1,756 triple e C battiti A in 1,731 triple - numeri quasi identici. Sulla base di questo calcolo e delle simulazioni di dadi con più di sei facce, ha ipotizzato la squadra che quando il numero di lati sui dadi si avvicina all'infinito, la probabilità che A battiti C si avvicina al 50%.

La congettura, con la sua miscela di accessibilità e sfumature, ha colpito Conrey come un buon foraggio per un progetto Polymath, in cui molti matematici si riuniscono online per condividere idee. A metà del 2017, ha proposto l'idea a Gowers, il creatore dell'approccio Polymath. "Mi è piaciuta molto la domanda, per il suo valore di sorpresa", ha detto Gowers. Ha scritto un post sul blog sulla congettura che ha attirato una raffica di commenti e, nel corso di altri sei post, i commentatori sono riusciti a dimostrarlo.

Nel loro articolo, pubblicato on-line alla fine di novembre 2022, una parte fondamentale della prova consiste nel dimostrare che, per la maggior parte, non ha senso parlare del fatto che un singolo dado sia forte o debole. I dadi di Buffett, nessuno dei quali è il più forte del branco, non sono così insoliti: se scegli un dado a caso, ha mostrato il progetto Polymath, è probabile che batta circa la metà degli altri dadi e perda contro l'altra metà. "Quasi ogni dado è piuttosto nella media", ha detto Gowers.

Il progetto si è discostato dal modello originale del team AIM per un aspetto: per semplificare alcuni aspetti tecnici, il progetto ha dichiarato che l'ordine dei numeri su un dado è importante, quindi, ad esempio, 122556 e 152562 sarebbero considerati due dadi diversi. Ma il risultato di Polymath, combinato con le prove sperimentali del team AIM, crea una forte presunzione che la congettura sia vera anche nel modello originale, ha detto Gowers.

"Sono stato assolutamente felice che abbiano trovato questa prova", ha detto Conrey.

Quando si trattava di raccogliere quattro o più dadi, il team AIM aveva previsto un comportamento simile a quello di tre dadi: ad esempio, se A battiti B, B battiti C ed C battiti D allora dovrebbe esserci una probabilità di circa il 50-50 che D battiti A, avvicinandosi esattamente a 50-50 man mano che il numero di lati sui dadi si avvicina all'infinito.

Per testare la congettura, i ricercatori hanno simulato tornei testa a testa per gruppi di quattro dadi con 50, 100, 150 e 200 lati. Le simulazioni non obbedivano alle loro previsioni così strettamente come nel caso di tre dadi, ma erano comunque abbastanza vicine da rafforzare la loro convinzione nella congettura. Ma sebbene i ricercatori non se ne rendessero conto, queste piccole discrepanze portavano un messaggio diverso: per gruppi di quattro o più dadi, la loro congettura è falsa.

"Volevamo davvero che [la congettura] fosse vera, perché sarebbe stato bello", ha detto Conrey.

Nel caso di quattro dadi, Elisabetta Cornacchia del Politecnico federale di Losanna e Jan Hązła dell'African Institute for Mathematical Sciences di Kigali, Rwanda, ha mostrato in a carta pubblicato online alla fine del 2020 che se A battiti B, B battiti C ed C battiti D, poi D ha una probabilità leggermente superiore al 50% di battere A - probabilmente da qualche parte intorno al 52%, ha detto Hązła. (Come per il documento Polymath, Cornacchia e Hązła hanno utilizzato un modello leggermente diverso rispetto al documento AIM.)

La scoperta di Cornacchia e Hązła emerge dal fatto che sebbene, di norma, un singolo dado non sarà né forte né debole, una coppia di dadi può talvolta avere aree di forza comuni. Se prendi due dadi a caso, hanno mostrato Cornacchia e Hązła, c'è una buona probabilità che i dadi siano correlati: tenderanno a battere o perdere con gli stessi dadi. "Se ti chiedo di creare due dadi vicini l'uno all'altro, si scopre che questo è possibile", ha detto Hązła. Queste piccole sacche di correlazione spingono i risultati dei tornei lontano dalla simmetria non appena ci sono almeno quattro dadi nell'immagine.

I giornali recenti non sono la fine della storia. L'articolo di Cornacchia e Hązła inizia solo a scoprire esattamente come le correlazioni tra i dadi sbilanciano la simmetria dei tornei. Nel frattempo, però, ora sappiamo che ci sono un sacco di set di dadi intransitivi là fuori, forse anche uno abbastanza sottile da indurre Bill Gates a scegliere per primo.