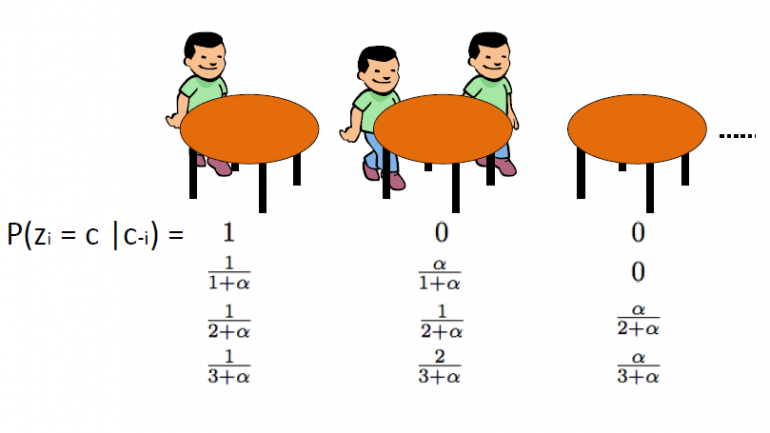Il processo Dirichlet il processo del ristorante cinese e altre rappresentazioni

• 20 Maggio 2014
• Vasilis Vryniotis
• . Non ci sono commenti

Questo articolo è la terza parte della serie sul clustering con i modelli di miscele di processo di Dirichlet. La volta precedente abbiamo definito il modello di miscela finita basato su Dirichlet Distribution e abbiamo posto domande su come rendere infinito questo particolare modello. Abbiamo brevemente discusso l'idea di prendere il limite del modello quando il numero k di cluster tende all'infinito, ma come abbiamo sottolineato l'esistenza di un tale oggetto non è banale (in altre parole, come possiamo effettivamente “prendere il limite di un modello “?). Come promemoria, il motivo per cui vogliamo prendere k infinito è perché in questo modo avremo un modello non parametrico che non ci richiede di predefinire il numero totale di cluster all'interno dei dati.

Aggiornamento: Datumbox Machine Learning Framework è ora open-source e gratuito scaricare. Dai un'occhiata al pacchetto com.datumbox.framework.machinelearning.clustering per vedere l'implementazione dei modelli di miscela di processo di Dirichlet in Java.

Anche se il nostro obiettivo è costruire un modello in grado di eseguire il clustering su set di dati, prima di questo dobbiamo discutere dei processi di Dirichlet. Forniremo sia le rigorose definizioni matematiche sia le spiegazioni più intuitive di DP e discuteremo dei modi per costruire il processo. Queste costruzioni / rappresentazioni possono essere viste come un modo per trovare le occorrenze del processo di Dirichlet nella "vita reale".

Nonostante abbia cercato di adattare il mio rapporto di ricerca in modo tale che questi post sul blog siano più facili da seguire, è ancora importante definire gli strumenti matematici e le distribuzioni necessarie prima di iniziare a utilizzare i modelli. I modelli di processo di Dirichlet sono un argomento di ricerca attiva, ma richiedono una buona conoscenza delle statistiche e dei processi stocastici prima di utilizzarli. Un altro problema è che, come vedremo in questo articolo, i processi di Dirichlet possono essere rappresentati / costruiti in numerosi modi. Di conseguenza diversi documenti accademici usano notazioni / convenzioni completamente diverse ed esaminano il problema da diversi punti di vista. In questo post provo a spiegarli nel modo più semplice possibile e utilizzo la stessa notazione. Speriamo che le cose diventino più chiare con i due prossimi articoli che si concentrano sulla definizione di Dirichlet Process Mixture Models e su come usarli effettivamente per eseguire analisi di cluster.

1. Definizione del processo Dirichlet

Un processo di Dirichlet su uno spazio is è un processo stocastico. È una distribuzione di probabilità su "distribuzioni di probabilità su Θ spazio" e a trarre da esso è una distribuzione discreta. Più formalmente una distribuzione di Dirichlet è una distribuzione su misure di probabilità. UN misura di probabilità è una funzione di sottoinsiemi di spazio da Θ a [0,1]. G è una misura di probabilità casuale distribuita DP, indicata come , se per qualsiasi partizione (A₁,…UN_n) dello spazio Θ abbiamo quello .

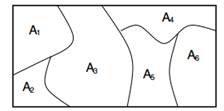
Figura 1: I margini su partizioni finite sono distribuiti da Dirichlet.

Il DP ha due parametri: il primo è la distribuzione di base G₀ che serve come un mezzo . Il secondo è il parametro di forza α che è strettamente positivo e serve come varianza inversa . Determina l'entità della ripetizione dei valori della distribuzione di output. Maggiore è il valore di a, minore è la ripetizione; minore è il valore, maggiore è la ripetizione dei valori della distribuzione dell'output. Infine, lo spazio Θ è lo spazio dei parametri su cui definiamo il DP. Inoltre lo spazio Θ è anche lo spazio di definizione di G₀ che è uguale a quello di G.

Un più semplice e di più modo intuitivo spiegare un processo di Dirichlet è il seguente. Supponiamo di avere uno spazio Θ che può essere partizionato in qualsiasi modo finito (A₁,…,UN_n) e una distribuzione di probabilità G che assegna loro le probabilità. La G è una distribuzione di probabilità specifica su Θ ma ce ne sono molte altre. Il processo Dirichlet su Θ modella esattamente questo; è una distribuzione su tutte le possibili distribuzioni di probabilità sullo spazio Θ. Il processo di Dirichlet è parametrizzato con G₀ funzione di base e parametro di concentrazione α. Possiamo dire che G è distribuito secondo DP con i parametri α e G₀ se la distribuzione congiunta delle probabilità che G assegna alle partizioni di Θ segue la distribuzione di Dirichlet. In alternativa possiamo dire che le probabilità che G assegna a qualsiasi partizione finita di Θ segue la distribuzione di Dirichlet.

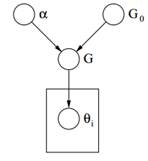
Figura 2: Modello grafico del processo Dirichlet

Finalmente sopra possiamo vedere il modello grafico di una DP. Dobbiamo notare che α è un iperparametro scalare, G₀ è la distribuzione di base di DP, G una distribuzione casuale su space spazio dei parametri campionato dalla DP che assegna le probabilità ai parametri e θ_i è un vettore di parametri che viene disegnato dalla distribuzione G ed è un elemento di Θ spazio.

2. Processi di Dirichlet posteriori

I processi di Dirichlet posteriori sono stati discussi da Ferguson. Iniziamo disegnando una misura di probabilità casuale G da un processo di Dirichlet, . Poiché G è una distribuzione di probabilità su Θ, possiamo anche campionare da questa distribuzione e disegnare campioni indipendenti distribuiti in modo identico θ₁, ..., θ_n ~ G. Dato che i disegni da un processo di Dirichlet sono distribuzioni discrete, possiamo rappresentare where è una breve notazione per che è una funzione delta che richiede 1 if e 0 altrove. Un effetto interessante di ciò è che, poiché G è definito in questo modo, esiste una probabilità positiva di campioni diversi aventi lo stesso valore . Come vedremo più avanti, questo crea un effetto di clustering che può essere utilizzato per eseguire l'analisi del cluster su set di dati.

Usando le definizioni e le osservazioni di cui sopra vogliamo stimare il posteriore del processo di Dirichlet dati i campioni θ. Tuttavia da quando lo sappiamo ed usando le Regole di Bayes e la Coniugazione tra Dirichlet e Multinomial abbiamo questo ed .

Equazione 1: processo di Dirichlet posteriore

Questa proprietà è molto importante ed è utilizzata dalle varie rappresentazioni DP.

3. Rappresentazioni del processo Dirichlet

Nei segmenti precedenti abbiamo definito il processo Dirichlet e presentato il suo modello teorico. Una domanda importante a cui dobbiamo rispondere è come sappiamo che esiste un tale oggetto e come possiamo costruire e rappresentare un processo di Dirichlet.

Le prime indicazioni di esistenza sono state fornite da Ferguson che ha usato il teorema di coerenza di Kolmogorov, ha dato la definizione di un processo di Dirichlet e ha descritto il processo di Dirichlet posteriore. Continuando la sua ricerca, Blackwell e MacQueen ha usato il teorema di De Finetti per dimostrare l'esistenza di una tale misura di probabilità casuale e ha introdotto lo schema dell'urna Blackwell-MacQueen che soddisfa le proprietà del processo di Dirichlet. Nel 1994 Seturaman ha fornito un ulteriore modo semplice e diretto per costruire un DP introducendo la costruzione Stick-breaking. Infine, un'altra rappresentazione è stata fornita da Aldous che ha introdotto il processo di ristorazione cinese come un modo efficace per costruire un processo Dirichlet.

Le varie rappresentazioni del processo di Dirichlet sono matematicamente equivalenti, ma la loro formulazione differisce perché esaminano il problema da diversi punti di vista. Di seguito presentiamo le rappresentazioni più comuni trovate in letteratura e ci concentriamo sul processo di ristorazione cinese che fornisce un modo semplice e computazionalmente efficiente per costruire algoritmi di inferenza per il processo di Dirichlet.

3.1 Lo schema dell'urna Blackwell-MacQueen

Lo schema dell'urna Blackwell-MacQueen può essere usato per rappresentare un processo di Dirichlet ed è stato introdotto da Blackwell e MacQueen. Si basa sullo schema dell'urna di Pólya che può essere visto come il modello opposto del campionamento senza sostituzione. Nello schema dell'urna Pólya assumiamo che abbiamo un'urna non trasparente che contiene palline colorate e disegniamo palline a caso. Quando disegniamo una palla, osserviamo il suo colore, la rimettiamo nell'urna e aggiungiamo una palla aggiuntiva dello stesso colore. Uno schema simile viene utilizzato da Blackwell e MacQueen per costruire un processo Dirichlet.

Questo schema produce una sequenza di θ₁, θ₂,… con probabilità condizionali . In questo schema assumiamo che G₀ è una distribuzione sui colori e ciascuno θ_n rappresenta il colore della palla che viene posizionata nell'urna. Il algoritmo è il seguente:

· Iniziamo con un'urna vuota.

· Con probabilità proporzionale a α disegniamo e aggiungiamo una palla di questo colore nell'urna.

· Con probabilità proporzionale a n-1 disegniamo una palla casuale dall'urna, ne osserviamo il colore, la rimettiamo all'urna e aggiungiamo una palla aggiuntiva dello stesso colore nell'urna.

In precedenza abbiamo iniziato con un processo Dirichlet e derivato lo schema Blackwell-MacQueen. Ora partiamo al contrario dallo schema Blackwell-MacQueen e ricaviamo la DP. Da θ_i sono stati disegnati in modo Iid da G, la loro distribuzione congiunta sarà invariante a eventuali permutazioni finite e quindi sono scambiabili. Di conseguenza, usando il teorema di De Finetti, abbiamo che deve esistere una distribuzione sulle misure per renderle possibili e questa distribuzione è il processo di Dirichlet. Di conseguenza dimostriamo che lo schema dell'urna Blackwell-MacQueen è una rappresentazione di DP e ci offre un modo concreto per costruirlo. Come vedremo più avanti, questo schema è matematicamente equivalente al processo di ristorazione cinese.

3.2 La costruzione Stick-breaking

La costruzione Stick-breaking è un modo alternativo per rappresentare un processo Dirichlet che è stato introdotto da Seturaman. È un modo costruttivo di formare il distribuzione e utilizza il seguente analogia: Partiamo dal presupposto che abbiamo un bastone di lunghezza 1, lo spezziamo in posizione β₁ e assegniamo π₁ uguale alla lunghezza della parte del bastone che abbiamo rotto. Ripetiamo lo stesso processo per ottenere π₂, p₃,… eccetera; a causa del modo in cui questo schema è definito, possiamo continuare a farlo infinite volte.

Sulla base di quanto sopra il π_k può essere modellato come , Dove l' mentre come negli schemi precedenti, i θ vengono campionati direttamente dalla distribuzione Base . Di conseguenza, la distribuzione G può essere scritta come una somma di funzioni delta ponderate con π_k probabilità che è uguale a . Quindi la costruzione Stick-breaking ci offre un modo semplice e intuitivo per costruire un processo Dirichlet.

3.3 Il processo di ristorazione cinese

Il processo di ristorazione cinese, introdotto da Aldous, è un altro modo efficace per rappresentare un processo di Dirichlet e può essere direttamente collegato allo schema dell'urna di Blackwell-MacQueen. Questo schema utilizza il seguente analogia: Partiamo dal presupposto che esiste un ristorante cinese con infiniti tavoli. Quando i clienti entrano nel ristorante si siedono casualmente su uno dei tavoli occupati o scelgono di sedersi al primo tavolo vuoto disponibile.

Il CRP definisce una distribuzione sullo spazio delle partizioni degli interi positivi. Iniziamo disegnando θ₁, ... θ_n dallo schema dell'urna Blackwell-MacQueen. Come discusso nei segmenti precedenti, ci aspettiamo di vedere un effetto di raggruppamento e quindi il numero totale di valori θ unici k sarà significativamente inferiore a n. Pertanto, ciò definisce una partizione dell'insieme {1,2, ..., n} in k cluster. Di conseguenza, attingendo allo schema dell'urna Blackwell-MacQueen induce una partizione casuale dell'insieme {1,2, ..., n}. Il processo di ristorazione cinese è indotto distribuzione su partizioni. L'algoritmo è il seguente:

· Iniziamo con un ristorante vuoto.

· I 1 paesi^st il cliente è sempre attivo 1^st tavolo

· Il n + 1^th il cliente ha 2 opzioni:

o Siediti al 1 ° tavolo non occupato con probabilità

o Siediti su uno qualsiasi dei kth tavoli occupati con probabilità
where è il numero di persone sedute su quel tavolo

Dove α è il valore di dispersione di DP e n è il numero totale di clienti nel ristorante in un determinato momento. La variabile latente z_i memorizza il numero di tabella dell'i^th cliente e accetta valori da 1 a k_n dove k_n è il numero totale di tavoli occupati quando n clienti sono nel ristorante. Dovremmo notare che il k_n sarà sempre inferiore o uguale a n e in media si tratta di . Infine, dovremmo notare che la probabilità della disposizione dei tavoli è invariante alle permutazioni. Quindi la z_i è scambiabile il che implica che le tabelle con le stesse dimensioni dei clienti hanno la stessa probabilità.

Il processo del ristorante cinese è fortemente collegato al sistema dell'urna di Pólya e al processo di Dirichlet. Il CRP è un modo per specificare a distribuzione su partizioni (assegnazioni di tabella) di n punti e può essere utilizzato come precedente sullo spazio della variabile latente z_i quale determina le assegnazioni del cluster. Il CRP equivale allo schema dell'urna di Pólya con l'unica differenza che non assegna parametri a ciascuna tabella / cluster. Andare dal CRP allo schema dell'urna di Pólya disegniamo per tutte le tabelle k = 1,2… e poi per ogni x_i che è raggruppato nella tabella z_i assegnare a . In altre parole, assegnare alla nuova x_i il parametro θ della tabella. Finalmente da allora non possiamo assegnare da θ a infiniti tavoli dall'inizio, possiamo semplicemente assegnare un nuovo θ ogni volta che qualcuno si siede su un nuovo tavolo. A causa di tutto quanto sopra, il CRP può aiutarci a costruire algoritmi computazionalmente efficienti per eseguire l'analisi dei cluster su set di dati.

In questo post, abbiamo discusso il processo Dirichlet e diversi modi per costruirlo. Useremo le idee sopra nel prossimo articolo. Presenteremo il modello di miscela di processo di Dirichlet e utilizzeremo la rappresentazione cinese del ristorante per costruire il processo di Dirichlet e preformare l'analisi del cluster. Se hai perso alcuni punti, non preoccuparti perché le cose inizieranno a diventare più chiare con i prossimi due articoli.

Spero che tu abbia trovato questo post interessante. Se lo hai fatto, prenditi un momento per condividerlo su Facebook e Twitter. 🙂