Big O סימון וניתוח אלגוריתמים עם דוגמאות Python

מבוא

בדרך כלל ישנן מספר דרכים לפתור את הבעיה באמצעות תוכנת מחשב. לדוגמה, ישנן מספר דרכים למיין פריטים במערך - אתה יכול להשתמש מיזוג מיון, מיון בועות, מיון הכנסה, וכן הלאה. לכל האלגוריתמים הללו יש יתרונות וחסרונות משלהם ותפקידו של המפתח הוא לשקול אותם כדי שיוכל לבחור את האלגוריתם הטוב ביותר לשימוש בכל מקרה שימוש. במילים אחרות, השאלה העיקרית היא באיזה אלגוריתם להשתמש כדי לפתור בעיה ספציפית כאשר קיימים מספר פתרונות לבעיה.

ניתוח אלגוריתמים מתייחס לניתוח המורכבות של אלגוריתמים שונים ומציאת האלגוריתם היעיל ביותר לפתרון הבעיה העומדת על הפרק. סימון Big-O הוא מדד סטטיסטי המשמש לתיאור מורכבות האלגוריתם.

במדריך זה, ניקח תחילה סקירה קצרה של ניתוח אלגוריתמים ולאחר מכן נסתכל לעומק על סימון Big-O. נראה כיצד ניתן להשתמש בסימון Big-O כדי למצוא מורכבות אלגוריתם בעזרת פונקציות שונות של Python.

מדוע ניתוח אלגוריתם חשוב?

כדי להבין מדוע ניתוח אלגוריתמים חשוב, נעזר בדוגמה פשוטה. נניח שמנהל נותן משימה לשניים מעובדיו לעצב אלגוריתם ב-Python שמחשב את הפקטוריאלי של מספר שהוזן על ידי המשתמש. האלגוריתם שפיתח העובד הראשון נראה כך:

def fact(n):
    product = 1
    for i in range(n):
        product = product * (i+1)
    return product

print(fact(5))

שימו לב שהאלגוריתם פשוט לוקח מספר שלם כארגומנט. בתוך ה fact() פונקציה משתנה בשם product מאותחל ל 1. לולאה מבוצעת מ 1 ל n ובמהלך כל איטרציה, הערך ב- product מוכפל במספר המוחזר על ידי הלולאה והתוצאה מאוחסנת ב- product משתנה שוב. לאחר ביצוע הלולאה, ה- product המשתנה יכיל את הפקטוריאלי.

באופן דומה, העובד השני פיתח גם אלגוריתם שמחשב את הפקטוריאלי של מספר. העובד השני השתמש בפונקציה רקורסיבית כדי לחשב את הפקטוריאלי של המספר n:

def fact2(n):
    if n == 0:
        return 1
    else:
        return n * fact2(n-1)

print(fact2(5))

המנהל צריך להחליט באיזה אלגוריתם להשתמש. לשם כך, הם החליטו לבחור איזה אלגוריתם פועל מהר יותר. אחת הדרכים לעשות זאת היא על ידי מציאת הזמן הנדרש לביצוע הקוד באותו קלט.

במחברת Jupyter, אתה יכול להשתמש ב- %timeit מילולי ואחריו הקריאה לפונקציה כדי למצוא את הזמן שלוקח לפונקציה לביצוע:

%timeit fact(50)

זה ייתן לנו:

9 µs ± 405 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

הפלט אומר שהאלגוריתם לוקח 9 מיקרו שניות (פלוס/מינוס 45 ננו-שניות) לכל לולאה.

באופן דומה, אנו יכולים לחשב כמה זמן לוקח לגישה השנייה לביצוע:

%timeit fact2(50)

זה יביא ל:

15.7 µs ± 427 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

האלגוריתם השני הכולל רקורסיה לוקח 15 מיקרו שניות (פלוס/מינוס 427 ננו-שניות).

זמן הביצוע מראה שהאלגוריתם הראשון מהיר יותר בהשוואה לאלגוריתם השני הכולל רקורסיה. כאשר מתמודדים עם תשומות גדולות, ההבדל בביצועים יכול להיות משמעותי יותר.

עם זאת, זמן ביצוע אינו מדד טוב למדידת המורכבות של אלגוריתם מכיוון שהוא תלוי בחומרה. יש צורך במדד ניתוח מורכבות אובייקטיבי יותר עבור אלגוריתם. זה המקום שבו ה סימון ביג או מגיע לשחק.

ניתוח אלגוריתמים עם סימון Big-O

סימון Big-O מסמל את הקשר בין הקלט לאלגוריתם לבין השלבים הנדרשים לביצוע האלגוריתם. הוא מסומן ב-"O" גדול ואחריו סוגרי פתיחה וסגירה. בתוך סוגריים, היחס בין הקלט והצעדים שננקטו על ידי האלגוריתם מוצג באמצעות "n".

המפתח הוא - Big-O לא מעוניין ב- מסוים מופע שבו אתה מפעיל אלגוריתם, כגון fact(50), אלא, כמה טוב זה סולם בהינתן קלט הולך וגדל. זהו מדד הרבה יותר טוב להערכה מאשר זמן קונקרטי למופע קונקרטי!

לדוגמה, אם יש א קשר ליניארי בין הקלט לשלב שננקט על ידי האלגוריתם להשלמת ביצועו, סימון Big-O בו נעשה שימוש יהיה O (n). באופן דומה, סימון Big-O עבור פונקציות ריבועיות is O (n²).

כדי לבנות אינטואיציה:

• O (n): בשעה n=1, נעשה צעד אחד. בְּ n=10, ננקטים 10 צעדים.
• O (n²): בשעה n=1, נעשה צעד אחד. בְּ n=10, ננקטים 100 צעדים.

At n=1, שני אלה יבצעו אותו דבר! זוהי סיבה נוספת לכך שהתבוננות בקשר בין הקלט ומספר השלבים לעיבוד הקלט עדיפה על רק הערכת פונקציות עם קלט קונקרטי כלשהו.

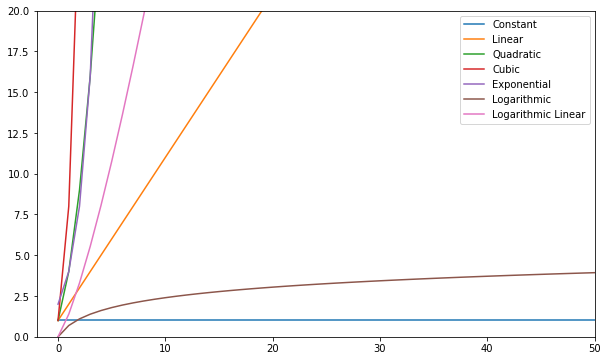
להלן כמה מהפונקציות הנפוצות ביותר של Big-O:

שם	O הגדול
קָבוּעַ	O (c)
לינארי	O (n)
ריבועית	O (n²)
מעוקב	O(n³)
מעריכים	O(2ⁿ)
לוגריתמי	O (יומן (n))
Log Linear	O(nlog(n))

אתה יכול לדמיין את הפונקציות האלה ולהשוות ביניהן:

באופן כללי - כל דבר גרוע מליניארי נחשב למורכבות גרועה (כלומר לא יעיל) ויש להימנע ממנו במידת האפשר. מורכבות לינארית היא בסדר ובדרך כלל רוע הכרחי. לוגריתמי זה טוב. קבוע זה מדהים!

כדי לקבל מושג כיצד מחושב Big-O, בואו נסתכל על כמה דוגמאות למורכבות קבועה, ליניארית וריבועית.

מורכבות מתמדת - O(C)

אומרים שהמורכבות של אלגוריתם קבועה אם השלבים הנדרשים להשלמת ביצוע אלגוריתם נשארים קבועים, ללא קשר למספר התשומות. המורכבות הקבועה מסומנת על ידי O (c) איפה c יכול להיות כל מספר קבוע.

בוא נכתוב אלגוריתם פשוט ב-Python שמוצא את הריבוע של הפריט הראשון ברשימה ואז מדפיס אותו על המסך:

def constant_algo(items):
    result = items[0] * items[0]
    print(result)

constant_algo([4, 5, 6, 8])

בתסריט למעלה, ללא קשר לגודל הקלט, או מספר הפריטים ברשימת הקלט items, האלגוריתם מבצע רק 2 שלבים:

1. מציאת הריבוע של האלמנט הראשון
2. הדפסת התוצאה על המסך.

לפיכך, המורכבות נשארת קבועה.

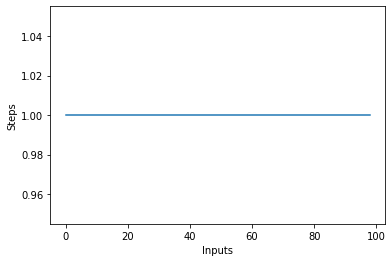
אם אתה מצייר עלילת קו עם הגודל המשתנה של items קלט בציר ה-X ומספר הצעדים בציר ה-Y, תקבל קו ישר. בואו ניצור תסריט קצר שיעזור לנו לדמיין זאת. לא משנה מספר הכניסות, מספר השלבים המבוצעים נשאר זהה:

steps = []
def constant(n):
    return 1
    
for i in range(1, 100):
    steps.append(constant(i))
plt.plot(steps)

מורכבות לינארית - O (n)

אומרים שהמורכבות של אלגוריתם היא ליניארית אם השלבים הנדרשים להשלמת ביצוע אלגוריתם גדלים או יורדים באופן ליניארי עם מספר התשומות. מורכבות ליניארית מסומנת על ידי O (n).

בדוגמה זו, בוא נכתוב תוכנית פשוטה שמציגה את כל הפריטים ברשימה למסוף:

def linear_algo(items):
    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

המורכבות של linear_algo() הפונקציה היא ליניארית בדוגמה שלעיל מכיוון שמספר האיטרציות של לולאת ה-for יהיה שווה לגודל הקלט items מערך. לדוגמה, אם יש 4 פריטים ב- items רשימה, ה-for-loop תתבצע 4 פעמים.

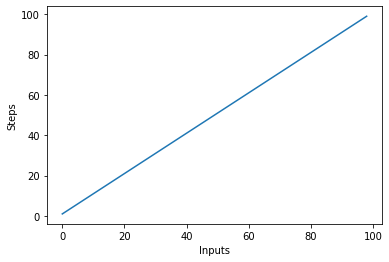
בואו ניצור במהירות עלילה עבור אלגוריתם המורכבות הליניארית עם מספר הכניסות בציר ה-x ומספר השלבים בציר ה-y:

steps = []
def linear(n):
    return n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

זה יביא ל:

דבר שחשוב לציין הוא שעם תשומות גדולות, הקבועים נוטים לאבד ערך. זו הסיבה שבדרך כלל אנו מסירים קבועים מסימון Big-O, וביטוי כגון O(2n) מקוצר בדרך כלל ל-O(n). גם O(2n) וגם O(n) הם ליניאריים - הקשר הליניארי הוא מה שחשוב, לא הערך הקונקרטי. לדוגמה, בואו נשנה את linear_algo():

def linear_algo(items):
    for item in items:
        print(item)

    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

ישנן שתי for-loops החוזרות על הקלט items רשימה. לכן מורכבות האלגוריתם הופכת O (2n), אולם במקרה של פריטים אינסופיים ברשימת הקלט, פעמיים של אינסוף עדיין שווה לאינסוף. אנחנו יכולים להתעלם מהקבוע 2 (מכיוון שהוא בסופו של דבר חסר משמעות) והמורכבות של האלגוריתם נשארת O (n).

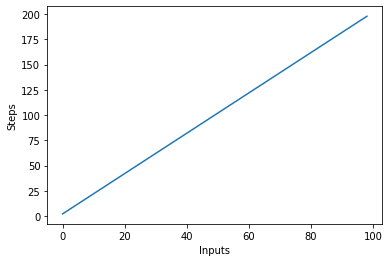
הבה נדמיין את האלגוריתם החדש הזה על ידי התוות הקלט על ציר ה-X ומספר השלבים על ציר ה-Y:

steps = []
def linear(n):
    return 2*n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

בתסריט למעלה, אתה יכול לראות את זה בבירור y=2nעם זאת, הפלט הוא ליניארי ונראה כך:

מורכבות ריבועית - O (n²)

אומרים שהמורכבות של אלגוריתם היא ריבועית כאשר השלבים הנדרשים לביצוע אלגוריתם הם פונקציה ריבועית של מספר הפריטים בקלט. מורכבות ריבועית מסומנת כ O (n²):

def quadratic_algo(items):
    for item in items:
        for item2 in items:
            print(item, ' ' ,item2)

quadratic_algo([4, 5, 6, 8])

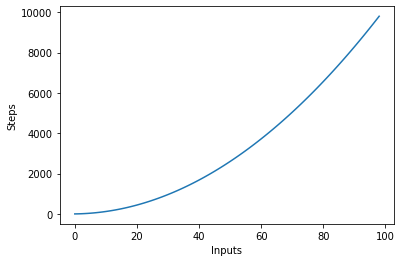
יש לנו לולאה חיצונית החוזרת דרך כל הפריטים ברשימת הקלט ולאחר מכן לולאה פנימית מקוננת, ששוב חוזרת דרך כל הפריטים ברשימת הקלט. המספר הכולל של השלבים שבוצעו הוא n*n, כאשר n הוא מספר הפריטים במערך הקלט.

הגרף הבא משרטט את מספר הכניסות מול השלבים עבור אלגוריתם בעל מורכבות ריבועית:

מורכבות לוגריתמית - O (logn)

אלגוריתמים מסוימים משיגים מורכבות לוגריתמית, כגון חיפוש בינארי. חיפוש בינארי מחפש אלמנט במערך, על ידי סימון ה- האמצע של מערך, וגיזום החצי שבו האלמנט לא נמצא. הוא עושה זאת שוב עבור החצי שנותר, וממשיך באותם השלבים עד שהאלמנט נמצא. בכל שלב, זה חצאים מספר האלמנטים במערך.

זה מחייב את המערך להיות ממוין, ועבורנו לעשות הנחה לגבי הנתונים (כגון שהם ממוינים).

כאשר אתה יכול להניח הנחות לגבי הנתונים הנכנסים, אתה יכול לנקוט בצעדים שמפחיתים את המורכבות של אלגוריתם. רצויה מורכבות לוגריתמית, מכיוון שהיא משיגה ביצועים טובים אפילו עם קלט בקנה מידה גבוה.

מוצאים את המורכבות של פונקציות מורכבות?

בדוגמאות קודמות, היו לנו פונקציות פשוטות למדי בקלט. עם זאת, כיצד אנו מחשבים את ה-Big-O של פונקציות המתקשרות (מרובות) לפונקציות אחרות בקלט?

בואו נסתכל:

def complex_algo(items):

    for i in range(5):
        print("Python is awesome")

    for item in items:
        print(item)

    for item in items:
        print(item)

    print("Big O")
    print("Big O")
    print("Big O")

complex_algo([4, 5, 6, 8])

בסקריפט שלמעלה מתבצעות מספר משימות, ראשית, מחרוזת מודפסת 5 פעמים על המסוף באמצעות print הַצהָרָה. לאחר מכן, נדפיס את רשימת הקלט פעמיים על המסך, ולבסוף, מחרוזת נוספת מודפסת שלוש פעמים בקונסולה. כדי למצוא את המורכבות של אלגוריתם כזה, עלינו לפרק את קוד האלגוריתם לחלקים ולנסות למצוא את המורכבות של החלקים הבודדים. סמן את המורכבות של כל חלק.

בחלק הראשון יש לנו:

for i in range(5):
	print("Python is awesome")

המורכבות של החלק הזה היא O (5) מכיוון שחמישה שלבים קבועים מבוצעים בקטע קוד זה ללא קשר לקלט.

לאחר מכן, יש לנו:

for item in items:
	print(item)

אנו יודעים שהמורכבות של פיסת הקוד לעיל היא O (n). באופן דומה, גם המורכבות של קטע הקוד הבא O (n):

for item in items:
	print(item)

לבסוף, בקטע הקוד הבא, מחרוזת מודפסת שלוש פעמים, ומכאן המורכבות O (3):

print("Big O")
print("Big O")
print("Big O")

כדי למצוא את המורכבות הכוללת, אנחנו פשוט צריכים להוסיף את המורכבויות האישיות האלה:

O(5) + O(n) + O(n) + O(3)

לפשט את האמור לעיל נקבל:

O(8) + O(2n) = O(8+2n)

אמרנו קודם שכאשר הקלט (שיש לו אורך n במקרה זה) הופך להיות גדול במיוחד, הקבועים הופכים לבלתי מובהקים כלומר פעמיים או מחצית מהאינסוף עדיין נשארים אינסוף. לכן, אנחנו יכולים להתעלם מהקבועים. המורכבות הסופית של האלגוריתם תהיה O (n)!

מורכבות המקרה הגרוע לעומת הטוב ביותר

בדרך כלל, כאשר מישהו שואל אותך על המורכבות של אלגוריתם - הוא מעוניין במורכבות במקרה הגרוע ביותר (Big-O). לפעמים, הם עשויים להתעניין גם במורכבות המקרה הטוב ביותר (ביג-אומגה).

כדי להבין את הקשר בין אלה, בואו נסתכל על פיסת קוד נוספת:

def search_algo(num, items):
    for item in items:
        if item == num:
            return True
        else:
            pass
nums = [2, 4, 6, 8, 10]

print(search_algo(2, nums))

בסקריפט למעלה, יש לנו פונקציה שלוקחת מספר ורשימת מספרים כקלט. הוא מחזיר אמת אם המספר שעבר נמצא ברשימת המספרים, אחרת הוא חוזר None. אם תחפשו 2 ברשימה, הם ימצאו בהשוואה הראשונה. זוהי מורכבות המקרה הטוב ביותר של האלגוריתם בכך שהפריט המבוקש נמצא באינדקס הראשון של החיפוש. מורכבות המקרה הטובה ביותר, במקרה זה, הוא O (1). מצד שני, אם תחפשו את 10, זה יימצא באינדקס האחרון של החיפושים. האלגוריתם יצטרך לחפש בכל הפריטים ברשימה, לפיכך המורכבות במקרה הגרוע ביותר הופך להיות O (n).

בנוסף למורכבות המקרה הטוב והרע, אתה יכול גם לחשב המורכבות הממוצעת (Big-Theta) של אלגוריתם, שאומר לך "בהינתן קלט אקראי, מהי מורכבות הזמן הצפויה של האלגוריתם"?

מורכבות בחלל

בנוסף למורכבות הזמן, שבה אתה סופר את מספר השלבים הנדרשים להשלמת ביצוע של אלגוריתם, אתה יכול גם למצוא את מורכבות חלל המתייחס לכמות השטח שאתה צריך להקצות בזיכרון במהלך ביצוע תוכנית.

בדוק את הדוגמה הבאה:

def return_squares(n):
    square_list = []
    for num in n:
        square_list.append(num * num)

    return square_list

nums = [2, 4, 6, 8, 10]
print(return_squares(nums))

אל האני return_squares() הפונקציה מקבלת רשימה של מספרים שלמים ומחזירה רשימה עם הריבועים המתאימים. האלגוריתם צריך להקצות זיכרון לאותו מספר פריטים כמו ברשימת הקלט. לכן, מורכבות החלל של האלגוריתם הופכת O (n).

סיכום

סימון Big-O הוא המדד הסטנדרטי המשמש למדידת המורכבות של אלגוריתם. במדריך זה, למדנו מהו סימון Big-O וכיצד ניתן להשתמש בו כדי למדוד את המורכבות של מגוון אלגוריתמים. למדנו גם סוגים שונים של פונקציות Big-O בעזרת דוגמאות Python שונות. לבסוף, סקרנו בקצרה את מורכבות המקרה הגרועה והטובה ביותר יחד עם מורכבות החלל.