מודל תערובת סופי המבוסס על חלוקת דיריצ'לט

• מאי 12, 2014
• וסיליס ווריניוטיס
• . 4 תגובות

פוסט בלוג זה הוא החלק השני בסדרת מאמרים על דגמי תערובת של Dirichlet Process. במאמר הקודם היה לנו סקירה כללית על מספר טכניקות ניתוח אשכול ושוחחנו על כמה מהבעיות / המגבלות העולות בשימוש בהן. יתר על כן, הצגנו בקצרה את דגמי התערובת של Dirichlet Process, דיברנו על הסיבה שהם מועילים והצגנו כמה מהיישומים שלהם.

עדכון: מסגרת הלמידה על מכונה של Datumbox היא כעת קוד פתוח וחינמית ל- להורדה. עיין בחבילה com.datumbox.framework.machinelearning.clustering כדי לראות את היישום של דגמי תערובת Dirichlet בתבנית Java.

דגמי תערובת התהליך Dirichlet יכולים להיות מעט קשה לבלוע בהתחלה בעיקר מכיוון שהם דגמי תערובת אינסופיים עם ייצוגים רבים ושונים. למרבה המזל דרך טובה לגשת לנושא היא להתחיל במודלים של תערובת סופית עם הפצת Dirichlet ואז לעבור לאינסוף.

כתוצאה מכך במאמר זה אציג בקצרה כמה התפלגויות חשובות שנצטרך, אנו נשתמש בהן כדי לבנות את ה- Dirichlet Prior עם מודל סיכון רב-שלומיניום ואז נעבור למודל התערובת הסופי המבוסס על התפלגות Dirichlet.

1. הפצת בטא

השמיים הפצת בטא היא משפחה של התפלגויות רצופות המוגדרות במרווח של [0,1]. הוא פרמטר על ידי שני פרמטרים חיוביים a ו- b וצורתו תלויה מאוד בבחירה של שני הפרמטרים הללו.

איור 1: התפלגות בטא לפרמטרים שונים של a, b

התפלגות בטא משמשת בדרך כלל למודל חלוקה על פני הסתברויות והיא בעלת צפיפות ההסתברות הבאה:

משוואה 1: PDF בטא

כאשר Γ (x) הוא פונקציית הגמא ו- a, b הפרמטרים של ההתפלגות. בטא משמש בדרך כלל כחלוקה של ערכי ההסתברות ונותן לנו את הסבירות שההסתברות המפורסמת שווה לערך מסוים P = p0. בהגדרתה, התפלגות בטא מסוגלת לדגמן את ההסתברות לתוצאות בינאריות הגוזלות ערכים נכונים או שקריים. הפרמטרים a ו- b יכולים להיחשב כמספרם הכספי של הצלחה וכישלון בהתאמה. לפיכך, התפלגות בטא מדגמת את ההסתברות להצלחה בהינתן הצלחות וכישלונות b.

2. התפלגות Dirichlet

השמיים הפצת Dirichlet היא ההכללה של התפלגות בטא עבור תוצאות מרובות (או במילים אחרות היא משמשת לאירועים עם תוצאות מרובות). זה פרמטר עם פרמטרים k א_i שחייב להיות חיובי. התפלגות Dirichlet שווה להתפלגות בטא כאשר מספר המשתנים k = 2.

איור 2: התפלגות Dirichlet עבור א_i פרמטרים

התפלגות Dirichlet משמשת בדרך כלל למודל חלוקה על פני הסתברויות והיא בעלת צפיפות ההסתברות הבאה:

משוואה 2: PDF Dirichlet

כאשר Γ (x) הוא פונקציית הגמא, p_i קח ערכים ב- [0,1] ו- Σp_i= 1. התפלגות Dirichlet מדגמת את ההפצה המשותפת של p_i ונותן את הסבירות ל- P₁=p₁,P₂=p₂, ...., ע_k-1=p_k-1 עם P_k= 1 - ΣP_i. כמו במקרה של ביתא, א_i פרמטרים יכולים להיחשב כפרזנטים של הופעות של כל אירוע i. התפלגות Dirichlet משמשת למודל ההסתברות של אירועים k יריבים, ולעיתים קרובות נקרא Dirichlet (א).

3. Dirichlet Prior עם סיכון רב-לומיאלי

כאמור, ניתן לראות את התפלגות Dirichlet כהפצה על פני התפלגויות הסתברות. במקרים בהם אנו רוצים לדגמן את ההסתברות לקרות אירועים k, תהיה גישה בייסית להשתמש סיכון רב-לאומי וסדרי עדיפויות .

להלן ניתן לראות את המודל הגרפי של מודל כזה.

איור 3: דגם גרפי של עדיפויות Dirichlet עם סיכון רב-שרירי

במודל הגרפי לעיל, α הוא וקטור ממדי ak עם ההיפר פרמטרים של Dirichlet קודמים, p הוא וקטור ממדי ak עם ערכי ההסתברות ו- x_i הוא ערך סקלרי מ- 1 ל- k המגלה לנו איזה אירוע התרחש. לבסוף נציין כי ה- P עוקב אחר התפלגות Dirichlet הפרמטר עם וקטור α וכך P ~ Dirichlet (α), ואילו x_i משתנים עוקבים אחר התפלגות הדיסקרטים (Multinomial) הפרמטר עם וקטור ההסתברויות p. ניתן להשתמש במודלים היררכיים דומים בסיווג המסמכים כדי לייצג את ההתפלגויות של תדרי מילות מפתח בנושאים שונים.

4. מודל תערובת סופי עם חלוקת דירייכל

על ידי שימוש בהפצת Dirichlet אנו יכולים לבנות א דגם תערובת סופי שניתן להשתמש בהם לביצוע אשכולות. נניח שיש לנו את המודל הבא:

משוואה 3: מודל תערובת סופית עם חלוקת דירייכל

המודל שלעיל מניח את הדברים הבאים: יש לנו מערך נתונים X עם n תצפיות ואנחנו רוצים לבצע עליו ניתוח אשכול. ה- k הוא מספר סופי קבוע המציג את מספר האשכולות / הרכיבים בהם נשתמש. ג_i משתנים מאחסנים את הקצאת האשכולות לתצפית X_i, הם לוקחים ערכים מ- 1 עד k ועוקבים אחר התפלגות בדידות עם הפרמטר p שהם הסתברות התערובת של הרכיבים. ה- F היא ההתפלגות הגנראטיבית של ה- X שלנו והיא פרמטר עם פרמטר אשר תלוי בהקצאת האשכולות של כל תצפית. בסך הכל יש לנו k ייחודי פרמטרים השווים למספר האשכולות שלנו. ה המשתנה מאחסן את הפרמטרים המפרמטרים את התפלגות F הגנרית ואנחנו מניחים שהוא עוקב אחר בסיס G₀ הפצה. המשתנה p מאחסן את אחוזי התערובת עבור כל אחד מאשכול k ועוקב אחר Dirichlet עם פרמטרים α / k. בסופו של דבר ה- α הוא וקטור ממדי ak עם ההיפר-פרמטרים (פסאודו-חשבונות) של התפלגות Dirichlet [2].

איור 4: דגם גרפי של מודל תערובת סופית עם חלוקת דירייכל

דרך פשוטה יותר ומתמטית פחות להסביר את המודל היא הבאה. אנו מניחים שניתן לקבץ את הנתונים שלנו באשכולות k. לכל אשכול פרמטרים משלו ופרמטרים אלה משמשים להפקת הנתונים שלנו. הפרמטרים מניחים לעקוב אחר תפוצה מסוימת של G₀. כל תצפית מיוצגת עם וקטור x_i ו- ac_i ערך המציין את האשכול אליו הוא שייך. כתוצאה מכך ג_i ניתן לראות כמשתנה העוקב אחר התפלגות הדיסקרטיות עם פרמטר p שאינו אלא הסתברויות התערובת, כלומר ההסתברות להתרחשות כל אשכול. בהתחשב בכך שאנו מטפלים בבעיה שלנו באופן בייסי, איננו מתייחסים לפרמטר p כאל וקטור לא ידוע קבוע. במקום זאת אנו מניחים כי ה- P עוקב אחר Dirichlet אשר פרמטר הוא על ידי פרפרמטר יתר hyper / k.

5. עבודה עם אשכולות K אינסופיים

מודל התערובת הקודם מאפשר לנו לבצע למידה ללא פיקוח, נוקט בגישה בייסית וניתן להרחיב אותה למבנה היררכי. עם זאת זהו מודל סופי מכיוון שהוא משתמש במספר קבוע מוגדר מראש של אשכולות. כתוצאה מכך היא מחייבת אותנו להגדיר את מספר הרכיבים לפני ביצוע ניתוח אשכול וכפי שדיברנו קודם ברוב היישומים זה לא ידוע ולא ניתן להעריך אותו בקלות.

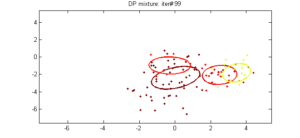
אחת הדרכים לפתור זאת היא לדמיין של- K יש ערך גדול מאוד הנוטה לאינסוף. במילים אחרות אנו יכולים לדמיין את גבול המודל הזה כאשר k נוטה לאינסוף. אם זה המקרה, אנו יכולים לראות שלמרות שמספר האשכולות k הוא אינסופי, המספר האמיתי של האשכולות הפעילים (אלה שיש להם לפחות תצפית אחת), אינו יכול להיות גדול מ- n (שהוא המספר הכולל של התצפיות במערך הנתונים שלנו). למעשה כפי שנראה בהמשך, מספר האשכולות הפעילים יהיה נמוך משמעותית מ- n והם יהיו פרופורציונאליים אליהם .

כמובן שלקחת את גבול ה- k לאינסוף אינה דבר של מה בכך. מספר שאלות עולות כמו האם ניתן לשים גבול כזה, איך היה נראה מודל זה ו כיצד ניתן לבנות ולהשתמש במודל כזה.

במאמר הבא נתמקד בדיוק בשאלות הללו: נגדיר את תהליך Dirichlet, נציג את הייצוגים השונים של DP ולבסוף נתמקד בתהליך המסעדה הסיני שהוא דרך אינטואיטיבית ויעילה לבנות תהליך Dirichlet.

אני מקווה שמצאת שהפוסט הזה מועיל. אם כן, אנא הקדש רגע לשתף את הכתבה בפייסבוק ובטוויטר. 🙂