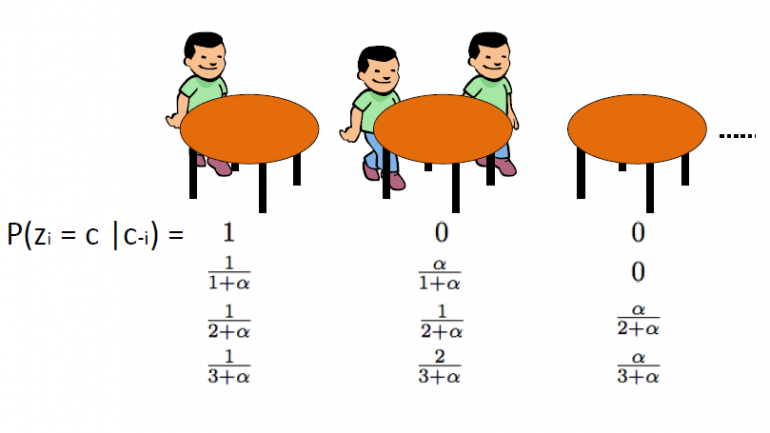Dirichlet מעבד את תהליך המסעדה הסיני וייצוגים אחרים

• מאי 20, 2014
• וסיליס ווריניוטיס
• . אין תגובה

מאמר זה הוא החלק השלישי של הסדרה על אשכולות עם דגמי תערובת של Dirichlet. בפעם הקודמת הגדרנו את מודל התערובת הסופית על בסיס הפצת Dirichlet והצגנו שאלות כיצד נוכל להפוך את המודל הספציפי הזה לאינסופי. דיברנו בקצרה על הרעיון של לקיחת גבול המודל כאשר מספר האשכולות k נוטה לאינסוף, אך כפי שהדגשנו כי קיומו של אובייקט כזה אינו טריוויאלי (במילים אחרות, כיצד אנו "לוקחים את גבול המודל" "?). כתזכורת, הסיבה לכך שאנו רוצים להפוך את k אינסופי היא מכיוון שבדרך זו יהיה לנו מודל לא פרמטרי שאינו מחייב אותנו להגדיר מראש את המספר הכולל של האשכולות שבתוך הנתונים.

עדכון: מסגרת הלמידה על מכונה של Datumbox היא כעת קוד פתוח וחינמית ל- להורדה. עיין בחבילה com.datumbox.framework.machinelearning.clustering כדי לראות את היישום של דגמי תערובת Dirichlet בתבנית Java.

למרות שהיעד שלנו הוא לבנות מודל שמסוגל לבצע אשכולות על מערכי נתונים, לפני כן עלינו לדון על תהליכי Dirichlet. אנו נספק הן את ההגדרות המתמטיות המחמירות והן את ההסברים האינטואיטיביים יותר של DP ונדון בדרכים לבניית התהליך. ניתן לראות במבנים / ייצוגים אלה דרך למצוא התרחשויות של תהליך Dirichlet ב"חיים האמיתיים ".

למרות שניסיתי להתאים את דוח המחקר שלי באופן שיהיה קל יותר לעקוב אחר פוסטים אלה בבלוג, עדיין חשוב להגדיר את הכלים וההפצות המתמטיות הדרושות לפני שנקפוץ להשתמש במודלים. מודלים של תהליך Dirichlet הם נושא למחקר פעיל, אך הם אכן דורשים הבנה טובה של הסטטיסטיקה והתהליכים הסטוכסטיים לפני השימוש בהם. בעיה נוספת היא שכפי שנראה במאמר זה, ניתן לייצג / לבנות תהליכי Dirichlet בדרכים רבות. כתוצאה מכך מספר מאמרים אקדמיים משתמשים בסימונים / מוסכמות שונות לחלוטין ובוחנים את הבעיה מנקודות מבט שונות. בפוסט זה אני מנסה להסביר אותם פשוטים ככל האפשר ולהשתמש באותה סימון. אני מקווה שהדברים יתבהרו עם שני המאמרים הקרובים המתמקדים בהגדרה של דגמי תערובת של Dirichlet תהליך וכיצד להשתמש בהם בפועל לניתוח אשכולות.

1. הגדרת תהליך Dirichlet

תהליך Dirichlet על מרחב Θ הוא תהליך סטוכסטי. זוהי חלוקת הסתברות על "התפלגויות הסתברות על שטח מרחב" ו- לצייר ממנו היא התפלגות דיסקרטית. באופן פורמלי יותר התפלגות Dirichlet היא חלוקה על פני מדדי הסתברות. א מדד הסתברות היא פונקציה של קבוצות משנה של המרחב Θ עד [0,1]. G הוא מדד הסתברות אקראי המופץ כ- אם למחיצה כלשהי (א₁,…א_n) של שטח Θ יש לנו את זה .

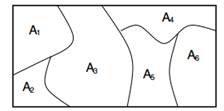
איור 1: שוליים במחיצות סופיות מופצים Dirichlet.

ל- DP שני פרמטרים: הראשון הוא חלוקת הבסיס G₀ שמשמש כמוצלח . השני הוא פרמטר החוזק α שהוא חיובי בהחלט ומשמש כמו שונות הפוכה . זה קובע את מידת החזרה של ערכי חלוקת הפלט. ככל שערך a גבוה יותר, כך החזרה קטנה יותר; ככל שהערך קטן יותר, כך החזרה על ערכי חלוקת הפלט גבוהה יותר. לבסוף מרחב Θ הוא מרחב הפרמטרים עליו אנו מגדירים את ה- DP. יתר על כן המרחב Θ הוא גם המרחב ההגדרה של G₀ שזהה לזה של ג.

פשוט יותר ויותר דרך אינטואיטיבית להסביר תהליך Dirichlet הוא הבא. נניח שיש לנו חלל Θ שניתן לחלק אותו בכל דרך סופית (א₁,…,א_n) ופיזור הסתברות G המקצה להם הסתברויות. ה- G הוא חלוקת הסתברות ספציפית על פני Θ אך ישנם רבים אחרים. תהליך ה- Dirichlet במודלים זה בדיוק; זוהי התפלגות על כל התפלגויות ההסתברות האפשריות במרחב Θ. תהליך Dirichlet פרמטר עם ה- G₀ פונקציית הבסיס ופרמטר הריכוז α. אנו יכולים לומר כי G מופץ על פי DP עם הפרמטרים α ו- G₀ אם ההתפלגות המשותפת של ההסתברויות ש- G מקצה למחיצות של Θ עוקבת אחר התפלגות Dirichlet. לחלופין אנו יכולים לומר כי ההסתברויות ש- G מקצה לכל מחיצה סופית של Θ נובעת מהפצת Dirichlet.

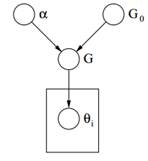
איור 2: דגם גרפי של תהליך Dirichlet

סוף סוף למעלה אנו יכולים לראות את מודל גרפי של DP. נציין כי α הוא hyperparameter סקלרי, G₀ היא חלוקת הבסיס של DP, G חלוקה אקראית על שטח פרמטר Θ שנדגם מה- DP שמקצה הסתברויות לפרמטרים ו- θ_i הוא וקטור פרמטרים שנשאב מההפצה של G והוא מהווה מרכיב במרחב Θ.

2. תהליכי Dirichlet אחורי

על תהליכי Dirichlet Posterior נדונו פרגוסון. אנו מתחילים בציור מדד הסתברות אקראי מתהליך Dirichlet, . מכיוון ש- G היא חלוקת הסתברות על פני Θ, אנו יכולים גם לדגום מההפצה הזו ולצייר דגימות מופצות זהות θ₁, ..., θ_n ~ G. מכיוון שציורים מתהליך Dirichlet הם התפלגות דיסקרטית, אנו יכולים לייצג איפה הוא סימון קצר עבור שהיא פונקציית דלתא שלוקחת 1 אם ו 0 במקום אחר. השפעה מעניינת מכך היא שמכיוון שמוגדרת G כך, קיימת הסתברות חיובית שלדגמים שונים בעלי אותו ערך . כפי שנראה בהמשך, זה יוצר אפקט אשכולות שניתן להשתמש בו לביצוע ניתוח אשכול במערכות נתונים.

באמצעות ההגדרות והתצפיות שלעיל אנו רוצים להעריך את האחורי של תהליך ה- Dirichlet בהינתן הדגימות θ. ובכל זאת מכיוון שאנו יודעים זאת ו על ידי שימוש בכללי Bayes והקשר בין Dirichlet ו- Multinomial יש לנו את זה ו .

משוואה 1: תהליך Dirichlet אחורי

מאפיין זה חשוב מאוד והוא משמש את ייצוגי העקורים השונים.

3. ייצוגי תהליכי Dirichlet

בקטעים הקודמים הגדרנו את תהליך Dirichlet והצגנו את המודל התיאורטי שלו. שאלה חשובה אחת שעלינו לענות עליה היא כיצד אנו יודעים שאובייקט כזה קיים ואיך אנו יכולים לבנות ולייצג תהליך Dirichlet.

האינדיקציות הראשונות לקיום נמסרו על ידי פרגוסון שהשתמש במשפט העקביות של קולמוגורוב, נתן את ההגדרה של תהליך Dirichlet ותיאר את תהליך Dirichlet Posterior. בהמשך המחקר שלו, בלקוול ומקווין השתמש במשפט דה-פינטי כדי להוכיח את קיומה של מדד הסתברותי אקראי כזה והציג את תוכנית הכדים של Blackwell-MacQueen המספקת את המאפיינים של תהליך Dirichlet. בשנת 1994 סתורמן סיפק דרך פשוטה וישירה נוספת לבניית DP באמצעות הצגת הקונסטרוקציה שבירת המקל. לבסוף סיפק ייצוג נוסף אלדוס שהציג את תהליך המסעדה הסיני כדרך יעילה לבנות תהליך Dirichlet.

הייצוגים השונים של תהליך ה- Dirichlet שקולים מבחינה מתמטית, אולם הניסוח שלהם שונה מכיוון שהם בוחנים את הבעיה מנקודות מבט שונות. להלן אנו מציגים את הייצוגים הנפוצים ביותר שנמצאים בספרות ואנו מתמקדים בתהליך המסעדה הסיני המספק דרך פשוטה ויעילה לחישוב לבנות אלגוריתמי הסקה לתהליך Dirichlet.

3.1 תוכנית הכדים של Blackwell-MacQueen

ניתן להשתמש בתכנית הכדיים Blackwell-MacQueen כדי לייצג תהליך Dirichlet והיא הוצגה על ידי בלקוול ומקווין. זה מבוסס על ערכת הכדים Pólya שניתן לראותה כמודל ההפוך של הדגימה ללא החלפה. בתכנית הכד של Pólya אנו מניחים שיש לנו כד שאינו שקוף המכיל כדורים צבעוניים ואנחנו מציירים כדורים באופן אקראי. כשאנחנו מציירים כדור אנו מתבוננים בצבעו, מחזירים אותו לכד ואנחנו מוסיפים כדור נוסף באותו צבע. תוכנית דומה משמשת לבלקוול וממקווין לבניית תהליך Dirichlet.

סכמה זו מייצרת רצף של θ₁, θ₂,… עם הסתברויות מותנות . בתכנית זו אנו מניחים ש- G₀ היא התפלגות על צבעים ועל כל θ_n מייצג את צבע הכדור שמונח בתוך הכד. ה אַלגוֹרִיתְם הוא כדלקמן:

· נתחיל בכד ריק.

· עם הסתברות פרופורציונלית ל α אנחנו מציירים ואנחנו מוסיפים כדור בצבע זה בכד.

· עם הסתברות פרופורציונלית ל- n-1 אנו שואבים כדור אקראי מהכד, אנו מתבוננים בצבעו, אנו ממקמים אותו בחזרה לכד ואנחנו מוסיפים כדור נוסף באותו צבע בכד.

בעבר התחלנו בתהליך Dirichlet והגענו לתוכנית Blackwell-MacQueen. עכשיו בואו נתחיל הפוך מתכנית Blackwell-MacQueen ונפיק את העקורים. מאז θ_i נמשכו באופן GID מתוך G, חלוקתם המשותפת תהיה ללא תחרות לכל תמורה סופית וכך הם ניתנים להחלפה. כתוצאה מכך על ידי שימוש במשפט של דה פינטי, אנו חייבים להתקיים התפלגות על אמצעים כדי לגרום להם לחלוקה, וההפצה הזו היא תהליך Dirichlet. כתוצאה מכך אנו מוכיחים שתכנית הכדים של Blackwell-MacQueen היא ייצוג של העקורים והיא נותנת לנו דרך קונקרטית לבנות אותה. כפי שנראה בהמשך, סכמה זו שקולה מתמטית לתהליך המסעדה הסיני.

3.2 הקונסטרוקציה שוברת המקל

הקונסטרוקציה שבירת המקל היא דרך חלופית לייצג תהליך Dirichlet שהונהג על ידי סתורמן. זוהי דרך קונסטרוקטיבית ליצור את הפצה ומשתמשת ב- בעקבות אנלוגיה: אנו מניחים שיש לנו מקל באורך 1, אנו שוברים אותו במיקום β₁ ואנחנו מקצים π₁ שווה לאורך החלק של המקל ששברנו. אנו חוזרים על אותו התהליך כדי להשיג π₂, פאי₃,… וכו; בגלל האופן בו מוגדרת סכמה זו אנו יכולים להמשיך לעשות זאת אינסוף פעמים.

בהתבסס על האמור לעיל ה- π_k ניתן למודל כ- , שם בעוד שכמו בסכימות הקודמות הדגימה θ נדגמת ישירות על ידי התפלגות הבסיס . כתוצאה מכך ניתן לכתוב את חלוקת ה- G כסכום של פונקציות דלתא המשוקללות עם π_k הסתברויות שהוא שווה ל . לפיכך, הקונסטרוקציה שבירת המקל מעניקה לנו דרך פשוטה ואינטואיטיבית לבנות תהליך Dirichlet.

3.3 תהליך המסעדה הסינית

תהליך המסעדה הסיני שהוצג על ידי אלדוס, היא דרך יעילה נוספת לייצג תהליך Dirichlet וניתן לקשר אותה ישירות לתכנית הכדים של Blackwell-MacQueen. בתכנית זו נעשה שימוש ב- בעקבות אנלוגיה: אנו מניחים שיש מסעדה סינית עם אינסוף שולחנות. כאשר הלקוחות נכנסים למסעדה הם יושבים באקראי לכל אחד מהשולחנות הכבושים או שהם בוחרים לשבת לשולחן הריק הראשון הזמין.

ה- CRP מגדיר חלוקה על שטח המחיצות של המספרים השלמים החיוביים. אנו מתחילים בציור θ₁, ... θ_n מתכנית הכדים של Blackwell-MacQueen. כפי שדיברנו בקטעים הקודמים, אנו מצפים לראות אפקט מקבץ וכך המספר הכולל של ערכי unique הייחודיים k יהיה פחות משמעותית מ- n. כך זה מגדיר מחיצה של הסט {1,2, ..., n} באשכולות k. כתוצאה מכך השרטוט מתכנית הכדים של Blackwell-MacQueen גורם למחיצה אקראית של הסט {1,2, ..., n}. תהליך המסעדה הסינית גורם לכך התפלגות על מחיצות. האלגוריתם הוא כדלקמן:

· מתחילים במסעדה ריקה.

· 1^st הלקוח יושב תמיד על 1^st שולחן

· ה- n + 1^th ללקוח יש שתי אפשרויות:

o שבו על השולחן הראשון ללא התעסקות בהסתברות

o שבו על אחד מהשולחנות הכבושים בק.ט. עם הסתברות
איפה הוא מספר האנשים שיושבים על השולחן הזה

כאשר α הוא ערך הפיזור של DP ו- n הוא המספר הכולל של הלקוחות במסעדה בזמן נתון. המשתנה הסמוי z_i שומר את מספר הטבלה של ה- i^th לקוח ולוקח ערכים מ- 1 עד k_n איפה ק_n הוא המספר הכולל של השולחנות הכבושים כאשר n לקוחות נמצאים במסעדה. נציין כי הק_n תמיד יהיה פחות או שווה ל- n ובממוצע זה בערך . לבסוף נציין כי ההסתברות לסידור שולחן אינו משתנה לפרמוטציות. כך הז_i ניתן להחלפה מה שמרמז שלטבלאות באותו גודל של לקוחות יש את אותה ההסתברות.

תהליך המסעדה הסיני קשור קשר הדוק לתכנית הכדים של Pólya ולתהליך Dirichlet. ה- CRP הוא דרך להגדיר א התפלגות על מחיצות (הקצאות טבלה) של n נקודות וניתן להשתמש בהן כקודם במרחב של משתנה סמוי z_i אשר קובע את משימות האשכול. ה- CRP שווה לתכנית הכדים של Pólya בהבדל היחיד שהיא אינה מקצה פרמטרים לכל טבלה / אשכול. ללכת מ- CRP לתכנית הכדים של פוליה אנחנו מציירים לכל הטבלאות k = 1,2 ... ואז לכל x_i המקובצת לטבלה z_i להקצות א . במילים אחרות להקצות ל- x החדש_i הפרמטר θ של הטבלה. סוף סוף מאז איננו יכולים להקצות את ה- θ לאינסוף טבלאות מההתחלה, אנחנו יכולים פשוט להקצות חדש θ בכל פעם שמישהו יושב על שולחן חדש. בשל כל האמור לעיל, ה- CRP יכול לעזור לנו לבנות אלגוריתמים יעילים חישוביים לביצוע ניתוח אשכול במערכות נתונים.

בפוסט זה דנו בתהליך Dirichlet ובמספר דרכים לבנות אותו. אנו נשתמש ברעיונות לעיל במאמר הבא. אנו נציג את מודל התערובת של Dirichlet Process ואנחנו נשתמש בייצוג המסעדות הסיני כדי לבנות את תהליך Dirichlet ו- Analyse Cluster Form. אם החמצת כמה נקודות אל תדאג כי הדברים יתחילו להתבהר עם שני המאמרים הבאים.

אני מקווה שמצאת את הפוסט הזה מעניין. אם כן, קח רגע לשתף אותו בפייסבוק ובטוויטר. 🙂