1מכון ICFO de Ciencies Fotoniques, המכון למדע וטכנולוגיה של ברצלונה, 08860 Castelldefels, ספרד
2CFIS-Centre de Formació Interdisciplinària Superior, UPC-Universitat Politècnica de Catalunya, 08028 ברצלונה, ספרד
3Univ Grenoble Alpes, CNRS, Grenoble INP, Institut Néel, 38000 Grenoble, France
4ICREA-Institucio Catalana de Recerca i Estudis Avançats, Lluis Companys 23, 08010 ברצלונה, ספרד
מצא את העיתון הזה מעניין או רוצה לדון? סקייט או השאירו תגובה ב- SciRate.
תַקצִיר
בסיסים בלתי מוטים הדדיים תואמים לזוגות מדידות שימושיים ביותר בתורת המידע הקוונטי. בממד המרוכב הקטן ביותר, שש, ידוע שקיימים בין שלושה לשבעה בסיסים בלתי מוטים הדדיים, כאשר השערה בת עשרות שנים, המכונה השערה של זאונר, קובעת כי קיימים שלושה לכל היותר. כאן אנו מתמודדים עם ההשערה של Zauner באופן מספרי באמצעות בניית אי-שוויון בל עבור כל זוג מספרים שלמים $n,d ge 2$ שניתן להפר באופן מקסימלי בממד $d$ אם ורק אם קיימים $n$ MUBs בממד זה. מכאן שאנו הופכים את ההשערה של זאונר לבעיית אופטימיזציה, שאנו מטפלים בה באמצעות שלוש שיטות מספריות: אופטימיזציה של נדנדה, תכנות חצי מוגדר לא ליניארי וטכניקות מונטה קרלו. כל שלוש השיטות מזהות נכון את המקרים הידועים בממדים נמוכים וכולן מציעות שלא קיימים ארבעה בסיסים בלתי מוטים הדדיים בממד שש, כאשר כולם מוצאים את אותם בסיסים שמייעלים באופן מספרי את אי השוויון המקביל של בל. יתרה מכך, נראה שהאופטימיזרים המספריים הללו עולים בקנה אחד עם "ארבעת הבסיסים הרחוקים ביותר" בממד שש, שנמצאו באמצעות אופטימיזציה מספרית של מדידת מרחק ב-[P. Raynal, X. Lü, B.-G. אנגלרט, {פיז. ר' א}, {83} 062303 (2011)]. לבסוף, תוצאות מונטה קרלו מצביעות על כך שלכל היותר שלושה MUBs קיימים בממד עשר.
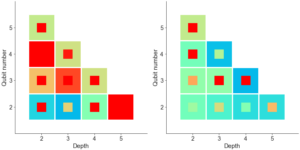
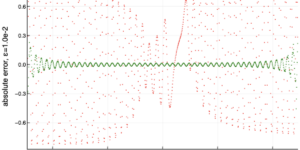
תמונה מוצגת: ההבדל היחסי בין הערך של אי-השוויון בל שלנו בהנחה ש-n MUBs קיימים בממד d לבין הערך שנמצא בשיטות המספריות שלנו. ערכים אפס פירושם שהשיטות מצאו n MUBs בממד d, בעוד שערכים שאינם אפס פירושם שהשיטות לא מצאו n MUBs בממד d. כל המקרים הידועים (ממדים שניים עד חמש וממד שש עם שניים ושלושה MUBs) מזוהים בצורה נכונה על ידי המספרים. בממד שש, אף אחת מהשיטות לא מוצאת ארבעה MUBs, וכל השיטות מתכנסות לאותה קבוצה של ארבעה בסיסים.
סיכום פופולרי
למרות השימוש הרחב שלהם, עדיין נותרו שאלות פתוחות בנוגע למבנה של MUBs. באופן הבולט ביותר, המספר המרבי של מדידות שאינן מוטות בזוגיות ("מספר MUBs") אינו ידוע אם הממד של המערכת הקוונטית הוא מספר מורכב. בפרט, בממד שש אנו יודעים רק שמספר ה-MUBs הוא בין שלושה לשבעה. השערה פתוחה ארוכת שנים היא זו של Zauner, הקובעת שאין יותר משלושה MUBs בממד שש. השערה זו בת עשרות שנים מגובה בכמה ראיות מספריות, אך אין הוכחות עד היום.
בעבודה זו אנו מתמודדים עם ההשערה של זאונר באמצעות אי-מקומיות של בל. אי-לוקאליות בל נוגעת לשני נסיינים שאינם מורשים לתקשר, אך יכולים לחלוק מתאמים מסוימים בצורה של אקראיות קלאסית או מצב קוונטי משותף. הוכח ששיתוף משאבים קוונטיים יכול להוביל לנתונים ניסיוניים שלא ניתן להסביר על ידי הפיזיקה הקלאסית (ליתר דיוק, על ידי מה שנקרא מודלים של משתנים מוסתרים מקומיים). זה ידוע כמשפט בל, והוא אומת בניסוי בעשור האחרון. עדות לאי-קלאסיות של נתונים ניסויים נעשית לרוב באמצעות מה שנקרא אי-שוויון בל, שהם פונקציות של הסתברויות תוצאות המדידה המתרחשות בניסוי. נתונים קלאסיים חייבים לספק את אי השוויון של בל, בעוד שנתונים קוונטיים עשויים להפר אותם.
לאחרונה, נמצאו אי-שוויון בל המופרים באופן מקסימלי אם אחד הצדדים משתמש בזוג מדידות MUB של מימד נתון. בעבודה זו, אנו מרחיבים את אי השוויון הללו לחדשים, המופרים באופן מקסימלי על ידי מספר נבחר של מדידות MUB בממד נתון. יתרה מכך, אם הממד בניסוי קבוע, ההפרה המקסימלית מתקבלת אם ורק אם המדידות המופעלות מתאימות למספר ה-MUB הנבחר בממד הנתון. לכן, ההחלטה אם קיים מספר נבחר של MUBs בממד נתון שווה ערך למציאת ההפרה המקסימלית של אי השוויון המקביל של Bell בממד קבוע זה.
למרות שמציאת ההפרה המקסימלית הזו היא בדרך כלל בעיה קשה, אנו משתמשים בשלוש שיטות מספריות שונות כניסיון למצוא את ההפרה המקסימלית של אי השוויון בל שלנו בממד קבוע. שתיים מהשיטות הללו הן גרסאות של טכניקות תכנות למחצה מוגדרות, בעוד שהשלישית בהשראת הפיזיקה הסטטיסטית ונקראת חישול מדומה. אמנם כל השיטות הללו הן היוריסטיות - כלומר, אין ערובה שהן ימצאו את האופטימום האמיתי של הבעיה - אפשר לאמוד את הביצועים שלהן על ידי יישום של בעיות אופטימיזציה שהאופטימום שלהן ידוע. בפרט, אנו מוצאים שכל שלוש השיטות מסוגלות לזהות נכון מדידות MUB במקרים בהם ידוע על קיומן. יתר על כן, במקרים שבהם ידוע שהם אינם קיימים, כל שלוש השיטות מתכנסות לאותה סט מדידות עד לדיוק מספרי. לאחר מכן אנו מיישמים את השיטות שלנו על המקרה הלא ידוע הראשון, כלומר, ארבעה MUBs בממד שש. אף אחת מהשיטות לא מסוגלת לזהות ארבעה MUBs בממד שש, אבל שוב כולם מתכנסים לאותה סט של ארבע מדידות עד לדיוק מספרי. יתר על כן, טכניקת החישול המדומה אינה מוצאת ארבעה MUBs בממד המרוכב הבא, ממד עשר. לכן, בעוד שלא ניתן להעלות טענות מחמירות בשל האופי ההיוריסטי של הטכניקות שלנו, התוצאות שלנו תומכות בהשערה של זאונר מנקודת המבט החדשה של אי-מקומיות של בל.
► נתוני BibTeX
► הפניות
[1] תעודת זהות איבנוביץ'. תיאור גיאומטרי של קביעת מצב קוונטי. Journal of Physics A: Mathematical and General, 14(12):3241–3245, 1981. doi:10.1088/0305-4470/14/12/019.
https://doi.org/10.1088/0305-4470/14/12/019
[2] G. Brassard CH Bennett. הצפנה קוונטית: הפצת מפתח ציבורי והטלת מטבעות. הליכים של הכנס הבינלאומי של IEEE בנושא מחשבים, מערכות ועיבוד אותות (IEEE, 1984), 175:8, 1984. doi:10.1016/j.tcs.2011.08.039.
https: / doi.org/â € ‹10.1016 / j.tcs 2011.08.039
[3] ארתור ק. אקרט. הצפנה קוונטית מבוססת על משפט בל. פיזי. Rev. Lett., 67:661–663, 1991. doi:10.1103/PhysRevLett.67.661.
https: / / doi.org/ 10.1103 / PhysRevLett.67.661
[4] דגמר ברוס. האזנת סתר אופטימלית בהצפנה קוונטית עם שישה מצבים. פיזי. Rev. Lett., 81:3018–3021, 1998. doi:10.1103/PhysRevLett.81.3018.
https: / / doi.org/ 10.1103 / PhysRevLett.81.3018
[5] ארמין טבאקולי, אלי המידי, ברנו מרקס ומוחמד בורננה. קודי גישה אקראית קוונטית באמצעות מערכות בודדות ברמת $d$. פיזי. Rev. Lett., 114:170502, 2015. doi:10.1103/PhysRevLett.114.170502.
https: / / doi.org/ 10.1103 / PhysRevLett.114.170502
[6] Máté Farkas ו-Jędrzej Kaniewski. בדיקה עצמית של בסיסים חסרי פניות הדדיים בתרחיש ההכנה והמדידה. פיזי. Rev. A, 99:032316, 2019. doi:10.1103/PhysRevA.99.032316.
https: / / doi.org/ 10.1103 / PhysRevA.99.032316
[7] ה' בכמן-פאסקינוצ'י ונ' גיסין. אי שוויון פעמון עבור qunits עם מדידות בינאריות. מידע קוונטי. Comput., 3(2):157–164, 2003. doi:10.26421/QIC3.2-6.
https: / doi.org/â € ‹10.26421 / QIC3.2-6
[8] Jędrzej Kaniewski, Ivan Supić, Jordi Tura, Flavio Baccari, Alexia Salavrakos, ו-Remigiusz Augusiak. אי-לוקאליות מרבית מהסתבכות מקסימלית ובסיסים בלתי מוטים הדדיים, ובדיקה עצמית של מערכות קוונטיות דו-קווטריות. Quantum, 3:198, 2019. doi:10.22331/q-2019-10-24-198.
https://doi.org/10.22331/q-2019-10-24-198
[9] ארמין טבאקולי, מאטה פרקאס, דניס רוסט, ז'אן-דניאל בנקל וג'דרז' קנייבסקי. בסיסים חסרי פניות הדדית ומדידות מידע סימטריות משלימות בניסויי בל. Science Advances, 7(7):eabc3847, 2021. doi:10.1126/sciadv.abc3847.
https://doi.org/10.1126/sciadv.abc3847
[10] תומס דורט, ברטולד-ג'ורג' אנגלרט, אינגמר בנגטסון וקרול ז'יצ'קובסקי. על בסיסים חסרי פניות הדדית. International Journal of Quantum Information, 08(04):535–640, 2010. doi:10.1142/S0219749910006502.
https: / / doi.org/ 10.1142 / S0219749910006502
[11] וויליאם ק ווטרס ובריאן די פילדס. קביעת מצב אופטימלית על ידי מדידות חסרות פניות הדדית. Annals of Physics, 191(2):363–381, 1989. doi:10.1016/0003-4916(89)90322-9.
https://doi.org/10.1016/0003-4916(89)90322-9
[12] פאוול ווצ'אן ותומס בת'. בנייה חדשה של בסיסים ללא משוא פנים במידות ריבועיות. מידע קוונטי. Comput., 5(2):93–101, 2005. doi:10.26421/QIC5.2-1.
https: / doi.org/â € ‹10.26421 / QIC5.2-1
[13] מיהאלי ויינר. פער למספר המרבי של בסיסים חסרי פניות הדדית. פרוק. עאמר. מתמטיקה. Soc., 141:1963–1969, 2013. doi:10.1090/S0002-9939-2013-11487-5.
https://doi.org/10.1090/S0002-9939-2013-11487-5
[14] גרהרד זאונר. Quantendesigns: Grundzüge einer nichtkommutativen Designtheorie. עבודת דוקטורט, 1999.
[15] פ' אוסקר בויקין, מירה סיתראם, פאם הואו טייפ ופאוול ווצ'אן. בסיסים בלתי מוטים הדדיים ופירוק אורתוגונלי של אלגברות שקר. מידע קוונטי. Comput., 7(4):371–382, 2007. doi:10.26421/QIC7.4-6.
https: / doi.org/â € ‹10.26421 / QIC7.4-6
[16] סטיבן ברירלי וסטפן ויגרט. בניית בסיסים חסרי פניות הדדית בממד שש. פיזי. Rev. A, 79:052316, 2009. doi:10.1103/PhysRevA.79.052316.
https: / / doi.org/ 10.1103 / PhysRevA.79.052316
[17] פיליפ ג'מינג, מאטה מטולצ'י, פיטר מורה, פרנץ סולוסי ומיהאלי ויינר. בעיה כללית של פאולי ומשפחה אינסופית של שלישיות MUB בממד 6. Journal of Physics A: Mathematical and Theoretical, 42(24):245305, May 2009. doi:10.1088/1751-8113/42/24/ 245305.
https://doi.org/10.1088/1751-8113/42/24/245305
[18] גארי מקונל, הארי ספנסר ואפק טאהיר. עדויות בעד ונגד השערת ה-MUB של Zauner ב-$mathbb{C}^6$. 2021. doi:10.48550/arXiv.2103.08703.
https:///doi.org/10.48550/arXiv.2103.08703
[19] סנדר גריבלינג וסוון פולק. בסיסים בלתי מוטים הדדיים: אופטימיזציה פולינומית וסימטריה. 2021. doi:10.48550/arXiv.2111.05698.
https:///doi.org/10.48550/arXiv.2111.05698
[20] Ingemar Bengtsson, Wojciech Bruzda, Åsa Ericsson, Jan-Åke Larsson, Wojciech Tadej, ו- Karol Życzkowski. בסיסים חסרי פניות הדדית ומטריצות האמרד בסדר גודל שש. Journal of Mathematical Physics, 48(5):052106, 2007. doi:10.1063/1.2716990.
https: / / doi.org/ 10.1063 / 1.2716990
[21] פיליפ ריינל, שין לו וברטולד-ג'ורג' אנגלרט. בסיסים בלתי מוטים הדדית בשישה ממדים: ארבעת הבסיסים הרחוקים ביותר. פיזי. Rev. A, 83:062303, 2011. doi:10.1103/PhysRevA.83.062303.
https: / / doi.org/ 10.1103 / PhysRevA.83.062303
[22] Edgar A. Aguilar, Jakub J. Borkała, Piotr Mironowicz, ו-Marcin Pawłowski. קשרים בין בסיסים חסרי פניות הדדית וקודי גישה אקראית קוונטית. פיזי. Rev. Lett., 121:050501, 2018. doi:10.1103/PhysRevLett.121.050501.
https: / / doi.org/ 10.1103 / PhysRevLett.121.050501
[23] ניקולה ברונר, דניאל קוולקנטי, סטפנו פירוניו, ולריו סקראני וסטפני וונר. אי-לוקליות של פעמון. הכומר Mod. Phys., 86: 419–478, 2014. doi: 10.1103 / RevModPhys.86.419.
https: / / doi.org/ 10.1103 / RevModPhys.86.419
[24] MOSEK ApS. MOSEK Fusion API עבור C++ 9.2.49, 2021. כתובת אתר: https:///docs.mosek.com/9.2/cxxfusion/index.html.
https:///docs.mosek.com/9.2/cxxfusion/index.html
[25] Hiroshi Yamashita, Hiroshi Yabe, ו-Kouhei Harada. שיטה ראשונית-דואלית של נקודות פנימיות לתכנות חצי מוגדר לא ליניארי. תכנות מתמטי, 135(1):89–121, 2012. doi:10.1007/s10107-011-0449-z.
https: / / doi.org/ 10.1007 / s10107-011-0449-z
[26] סטיבן בויד וליבן וונדנברגה. אופטימיזציה קמורה. הוצאת אוניברסיטת קיימברידג ', 2004. doi: 10.1017 / CBO9780511804441.
https: / / doi.org/ 10.1017 / CBO9780511804441
[27] S. Kirkpatrick, CD Gelatt, ו-MP Vecchi. אופטימיזציה על ידי חישול מדומה. Science, 220(4598):671–680, 1983. doi:10.1126/science.220.4598.671.
https: / / doi.org/ 10.1126 / science.220.4598.671
[28] ניקולס מטרופוליס, אריאנה וו. רוזנבלוט, מרשל נ. רוזנבלוט, אוגוסטה ה. טלר ואדוארד טלר. משוואת חישובי מצב על ידי מכונות מחשוב מהירות. The Journal of Chemical Physics, 21(6):1087–1092, 1953. doi:10.1063/1.1699114.
https: / / doi.org/ 10.1063 / 1.1699114
[29] מיגל נבאסקוס, סטפנו פירוניו ואנטוניו אסין. מגביל את קבוצת המתאמים הקוונטיים. פיזי. Rev. Lett., 98:010401, 2007. doi:10.1103/PhysRevLett.98.010401.
https: / / doi.org/ 10.1103 / PhysRevLett.98.010401
מצוטט על ידי
מאמר זה מתפרסם בקוונטים תחת התקציב ייחוס Creative Commons 4.0 הבינלאומי (CC BY 4.0) רישיון. זכויות יוצרים נשארות עם בעלי זכויות היוצרים המקוריים כמו המחברים או מוסדותיהם.